高压煤油恒速液动机转子倾覆现象的理论研究
于 斌,付 宁,权云晴,李红岩,孙东宁
(1.北京精密机电控制设备研究所,北京,100076;2.航天伺服驱动与传动技术实验室,北京,100076)
0 引 言
高压煤油恒速液动机是中国新一代煤油燃料火箭伺服系统的关键动力元件,利用引流火箭发动机的高压煤油做功,将高压煤油的压力能转化为机械能,驱动航天伺服系统中的液压泵旋转,为伺服作动器提供动作所需的充足、可靠的高压油液,以实现推力矢量控制,使火箭按照预定的轨迹和姿态飞行[1-5]。液动机是伺服机构动力转换的关键元件,其转子倾覆是后果非常严重的Ⅰ类故障模式,一旦发生将直接影响伺服机构的性能表现甚至功能实现[6-10]。
国内外的学者针对柱塞泵/液动机开展了较为深入的研究,美国密苏里-哥伦比亚大学Manring的研究表明,离心力矩造成的缸体和滑靴倾覆限制了柱塞泵转速的提高,并据此提出了缸体中心弹簧和压盘弹簧预压缩力应该满足的条件,通过相关因素无量纲化研究,发现泵的最高转速与泵的最大排量的三次方根的倒数成反比[11-14];Borghi 等[15]研究了高转速下的滑靴离心力矩,推导了滑靴失稳的临界速度,并分析了相关因素的影响;张军辉等[16]通过仿真和试验研究了高速轴向柱塞泵中柱塞组件质量不平衡引起的缸体倾覆现象,建立了柱塞组件质量不平衡量与缸体倾覆力矩的关系;潮群[17]对柱塞滑靴组件惯性力引起的倾覆力矩进行了理论推导和试验验证,建立了惯性力与倾覆力矩之间的数学关系,分析了缸体倾覆对柱塞滑靴组件的质量误差和缸孔尺寸误差的敏感性;权云晴[18]研究了伺服泵的抗倾覆能力,提出了一种基于浮板配流的解决方案,并进行了理论分析与试验验证。但是对于转子倾覆现象和机理尚未进行系统性的分析和阐述,尚未建立统一化的力学模型,尚未对转子连续运转时变过程中的倾覆现象进行分析。
1 液动机的转子倾覆现象及机理
伺服系统中的恒速煤油液动机,主要结构如图1所示,液动机的柱塞安装在转子的柱塞孔内形成圆柱副,滑靴安装在垫盘上形成平面副,滑靴与柱塞通过球面副连接,转子与花键轴通过圆柱副实现径向定位和支撑,转子与配流盘形成平面副并始终保持贴紧。

图1 液动机外形Fig.1 Outward appearance of the hydraulic motor
转子和柱塞组件在鼓形花键轴的支撑力、垫盘的支撑力以及配流盘的支撑力共同作用下,一同绕主轴的轴线旋转,同时承受由旋转产生的离心力的作用。在这些力的共同作用下,液动机转子底面与配流盘之间还能保持紧密贴合,实现配流盘上高低压油孔之间的隔离,这是液动机正常工作的必要条件。如果由于某种原因,液动机的转子与配流盘之间发生了分离,即转子倾覆,配流盘上高低压油孔将直接连通。这时液动机的引流流量出现骤增,而转速不会出现与流量相匹配的增加,甚至会出现转速下降乃至停转。
按照转子发生倾覆的原因,本文将转子倾覆划分为主动倾覆和被动倾覆两类。
主动倾覆是指转子剩余压紧力或者倾覆力矩设计不合理导致的转子在运转中主动发生的倾覆,即在正常受力情况下,转子“自发”的倾覆。其诱因包括剩余压紧力不足以及倾覆力矩过大。
被动倾覆是指转子剩余压紧力和剩余压紧力矩设计合理,但是液动机在特定工况下工作时,转子仍会发生倾覆。这时不是转子“自发”的倾覆,而是在轴的强制约束下被迫发生的倾覆。其诱因包括转子的有效浮动性变差(有效浮动量变小)以及加工/装配误差/轴变形量过大。
2 主动倾覆的研究
2.1 研究对象的选取及基本假设
液动机的主动倾覆现象是剩余压紧力不足或倾覆力矩过大造成的,分析这类倾覆现象的前提是对转子和柱塞组件的运动和受力进行分析。因此,选取转子和所有(共计Z个)柱塞组件作为研究对象。
由于转子和柱塞组件在旋转过程中的实际受力状态非常复杂,在理论计算中引入如下假设:
a)各零部件为刚体,忽略零部件的受力变形;
b)各运动副均为理想流体润滑状态,忽略各运动副之间的摩擦力;
c)液动机回转角速度恒定,忽略瞬间加速或减速的影响;
d)忽略柱塞组件沿轴向往复运动的惯性力;
e)忽略各零部件受到的液动力;
f)忽略转子柱塞组件受到的壳体腔内部油液的作用力。
2.2 研究对象的受力分析
研究对象在回转过程中,受力状态以2π/Z为转角周期进行周期性变化,因此基本思路是:在一个周期内的任一角位置对研究对象进行受力分析,将回转过程视为在不同角位置下的一系列准静态过程,同时考虑回转产生的离心力的作用。将轴对转子的支撑力作用点取为坐标原点,建立坐标系分析研究对象的受力状况,如图2所示。

图2 转子柱塞组件的受力Fig.2 Forces on rotor and piston assemblies
a)滑靴副部位的支撑力。
对于第i个柱塞组件,受到垫盘的作用力为FNi,忽略柱塞组件轴向运动的惯性力,则FNi的轴向分量FNAi与柱塞腔压力对柱塞产生的作用力相平衡,则:
式中pi为当前第i个柱塞腔内的油液压力;d为柱塞的直径。
垫盘对柱塞组件的作用力FNi的法相分量FNTi为
式中γ为斜盘的倾角。
将FNi向坐标原点O进行等效变化,可以等效为两个力分量(轴向分量FNAi和法相分量FNTi)和三个力矩分量(Txi、Tyi、Tzi),并对Z个柱塞组件的等效力和力矩求和:
式中R为柱塞的分布圆半径;ϕi为第i个柱塞的角位置。
b)配流副部位的支撑力。
转子底部高压区油膜对转子的支撑力F0和支撑力矩M0,低压区油膜对转子的支撑力FF0和支撑力矩MM0,需要说明的是,图2 中的力矩M0+MM0方向为示意性的,实际方向未必按-x轴方向,有可能既有x轴分量也有y轴分量。即:
式中Ffilm为转子底部油膜对转子的支撑力;Mx,My和Mz分别为转子底部油膜对转子的支撑力矩沿x轴、y轴和z轴方向的分量。
c)轴的支撑力和中心弹簧的压紧力。
研究对象还受到鼓形花键的转矩TL径向支撑力Fr,且Fr的作用点在坐标原点O点处,不产生转矩。在转子内孔布置的中心弹簧对转子的压紧力为Fspr。
d)离心力的作用。
高速回转产生的离心力对研究对象的作用,将转子和柱塞组件所受离心力分开考虑。由于转子沿回转轴方向的结构是对称的,因此转子的离心力及其力矩为零;柱塞组件所受离心力及其产生的力矩可结合图3进行计算。
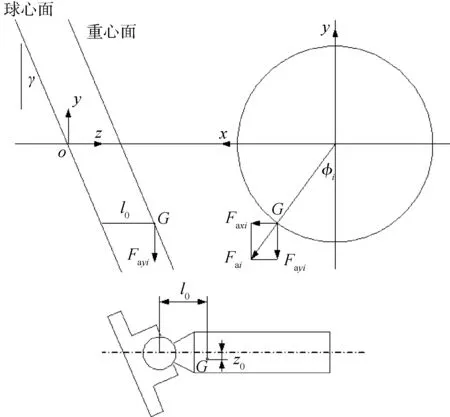
图3 柱塞组件i上的离心力Fig.3 Centrifugal force on piston i
柱塞组件i受到的离心力为
式中m为柱塞组件的质量;ω为转子的旋转角速度。柱塞组件i的离心力在各轴的分量为

式中l0为柱塞组件的重心在柱塞轴线上的投影与柱塞球心之间的距离。
所有柱塞组件的离心力对y轴的力矩为
所有柱塞组件的离心力对z轴的力矩为
由式(5)~(10)可知,柱塞组件的离心力合力为零,合力矩为
e)空间力系的简化与分析。
将上述作用于研究对象上的空间力系向坐标原点O进行等效简化,根据力和力矩的平衡方程,得到:
式中FA为研究对象受到的剩余压紧力;MTX和MTY分别为倾覆力矩MT沿x轴和y轴的分量。
式(12)第2 式中,轴对转子的径向支撑力Fr与斜盘对柱塞组件的径向力FNT相平衡,第3式中,Tz为液动机的输出力矩,与负载力矩TL相平衡。除去这两个平衡的等式最终得到图4所示的等效作用的合力和合力矩,其中MT为MTX和MTY的两个分量的合成力矩,其方向未必与z轴重合,但总会与过O点且在yOz平面内的一条射线重合。
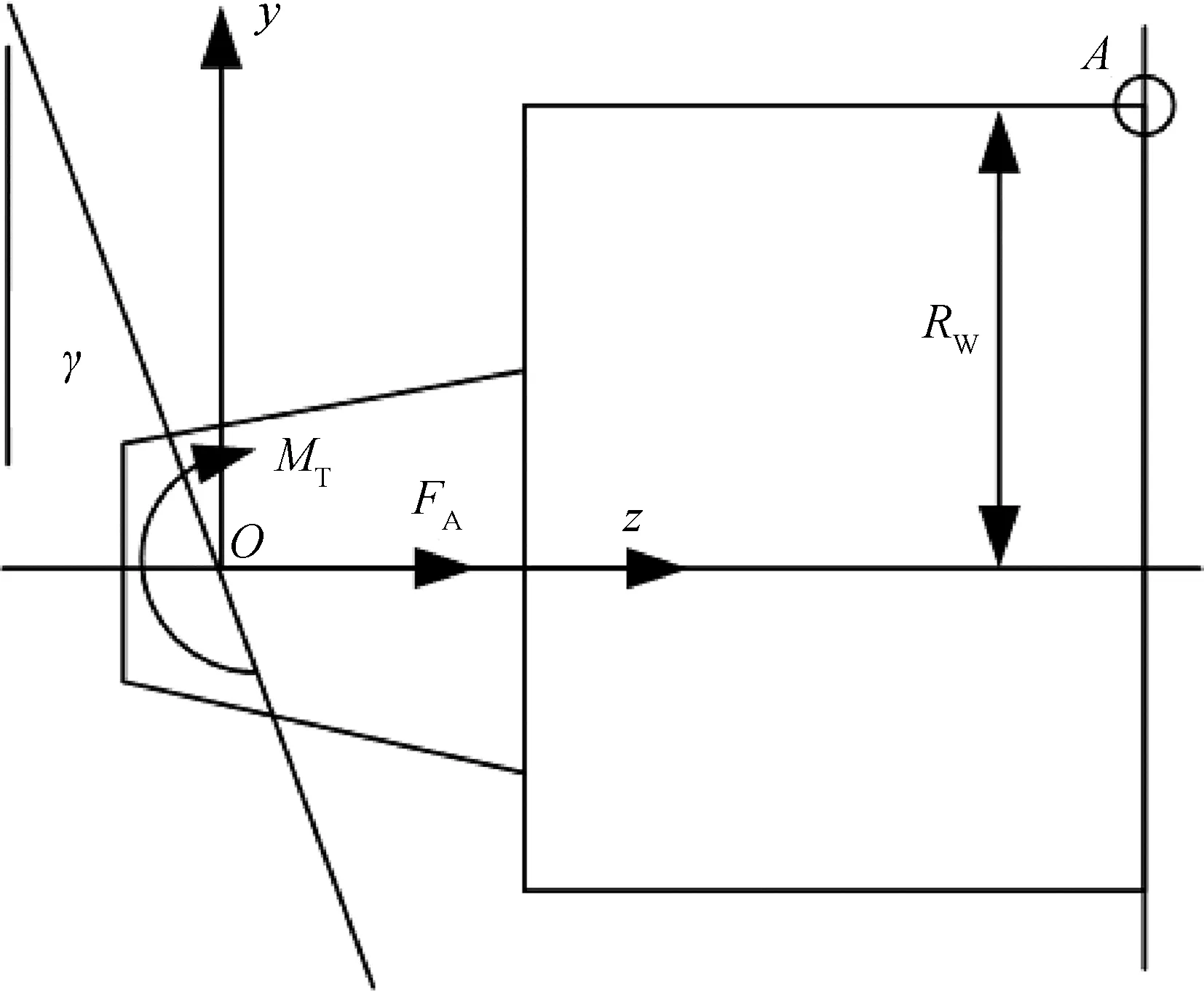
图4 转子柱塞组件的等效作用力和力矩Fig.4 Equivalent force and moment on rotor and piston assemblies
f)主动倾覆条件的数学表达。
根据图4所示的受力情况,在倾覆力矩MT的作用下转子具有绕底面外圆上的A点发生倾覆的倾向,而剩余压紧力FA对A点产生的力矩则会阻碍转子的倾覆。由此可以得出转子倾覆的临界条件为
也即:

为量化发生转子倾覆的风险,定义无量纲的倾覆安全系数α为
根据以上推导可知α∈(-∞,1],α=0为发生倾覆的临界条件,α越大越不容易发生倾覆,α越小越容易发生倾覆。
因此液动机转子不发生主动倾覆的设计原则为,在液动机所有可能出现的入口压力、出口压力、转速和负载条件下,在转子转过一个完整的转角周期2π/Z的过程中的任一角位置下,均有倾覆安全系数α>0,且应有一定的安全余量,以确保液动机在本文忽略的因素的客观影响下仍可以安全可靠运转。
3 被动倾覆的研究
液动机转子的被动倾覆是指液动机转子满足不发生主动倾覆的条件,但仍然出现的倾覆现象,是在轴的强制约束下发生的倾覆现象。
被动倾覆现象的出现,是由于转子的浮动性不能满足花键部位的旋转轴线与配流盘法线方向的偏差造成的,被动倾覆现象分析的主要理论基础是尺寸链的设计计算,计算内容较为简单,不作为重点研究内容,仅对被动倾覆现象的成因和过程进行介绍。
液动机转子与配流盘之间为平面接触,与轴之间通过内外花键的大径进行定位,两者之间为间隙配合,以保证转子在轴上有一定的径向浮动量。理想状态下转子回转轴线与配流盘法线方向一致,但零件加工中不可避免地存在一定的误差,而且正常工作中轴也存在一定的变形量,这些因素综合作用导致花键部位的回转轴线与配流盘的法线之间存在一定的夹角。如果这个夹角过大,转子与轴之间的间隙不能弥补夹角存在的影响,将会导致转子在轴的强制约束下随轴一起偏转,进而导致转子的底面与配流盘之间脱离,即出现倾覆现象。
图5为被动倾覆现象的示意,其中图5a为理想尺寸下的位置关系,转子与轴之间的花键配合采用大径定位,转子浮动量为δ0,转子底面与配流盘紧密贴合;图5b 为考虑轴的安装误差、轴的变形以及转子底面与内花键孔之间垂直度等各类公差累加,且公差累积较大,导致转子的浮动量完全被抵消,最终造成转子底面与配流盘之间分离,即转子发生被动倾覆。

图5 被动倾覆现象Fig.5 The passive capsizing
被动倾覆现象大都可以通过合理设计尺寸链、控制加工公差、适当提高内外花键间隙(即转子的径向浮动量)等手段来解决,一般都可以取得较为满意的效果。
4 结束语
对高压煤油恒速液动机的转子倾覆现象和机理进行介绍,将转子的倾覆现象分为主动倾覆与被动倾覆两种,并分别进行了研究;重点针对主动倾覆现象的力学模型进行了分析,建立了主动倾覆条件的数学表达,为定量表示倾覆风险,引入了无量纲的倾覆安全系数α。
由于研究对象的受力分析建立在一些假设条件基础上,忽略了一些影响较小的次要因素,因此与实际受力状态存在一定的偏差,但本文的研究方法和建立的数学模型仍具有重要的应用价值;对被动倾覆现象的原因进行了分析,提出了控制加工和配合公差、适当提高内外花键间隙(即转子的径向浮动量)等解决被动倾覆现象的有效手段;在产品设计中,应合理配置相关参数,避免出现主动倾覆和被动倾覆现象。

