翻转启闭机构设计与优化研究
萧 辉,郭锦炎,李玉龙,王金龙,刘宝龙
(1.北京航天发射技术研究所,北京,100076;2.中国人民解放军96901部队,北京,100091)
0 引 言
密闭门是压力罐的重要组成部分,其启闭性能的优劣决定了压力罐的方案可行性及其总体规模。该密闭门要求采用翻转启闭方式,开启前要求翻转载荷的回转支点向上运动一个高度以避开压力罐边上的控制模块,然后再进行翻转;翻转角度是以往压力罐翻转类机构的1.4 倍,驱动载荷是以往压力罐翻转类机构最大载荷的4.2 倍,采用以往的翻转机构根本无法实现。因此提出了多连杆接力、自动开闭锁技术方案。
综合考虑上述多个技术难点,在进行该压力罐密闭门启闭机构设计时,有必要引入多目标优化方法进行优化设计。多目标优化算法在工程领域的应用较为广泛[1],相对于数学规划法而言,在解决复杂的综合优化问题中,多目标遗传算法具有很大的优势[2],但对于大型重载启闭系统,因工程上约束较多,往往难以收敛。基于精英策略非支配排序遗传算法(Nondominated Sorting Genetic Algorithm ⅠⅠ,NSGA-ⅠⅠ)[3]能够提高求解效率和求解精度[4-5]。
本文结合压力罐启闭机构设计要求,采用机构功能运动化的步序开展了翻转启闭机构设计,引入基于精英策略非支配排序遗传算法,以启闭角度、启闭机构体积、最大驱动载荷为优化目标进行了铰点位置优化,最后结合数值仿真结果验证了方法的可行性和有效性。
1 机构设计
1.1 原理设计
机构设计的核心内容主要在于机构原理方案设计[6],典型的四连杆、三连杆机构在各类机械系统中已广泛使用。实践证明,这类机构具有很好的可靠性与互换性,这也是各类启闭系统广泛采用该类机构的原因。
为实现可靠启闭,启闭机构采用单作动缸的驱动模式;为实现大角度安全开启,采用多连杆串联续力的方式;为实现开启和关闭时的自动关闭锁,第一阶段的运动采用四连杆形式,将密闭门前端从锁座凹槽处滑出,关锁时运动反之。考虑到启闭过程的平稳性、机构占空间尽可能小的要求,将作动缸置于密闭门正中间,并采用曲柄将载荷传至左右两侧的执行机构。
根据上述目的和准则,在组合过程中,为了节约结构空间,可以考虑将不同子机构的部分杆共用,即“一杆两铰”[7]、“一杆多用”等方式,得到设计启闭机构原理方案如图1、图2所示。
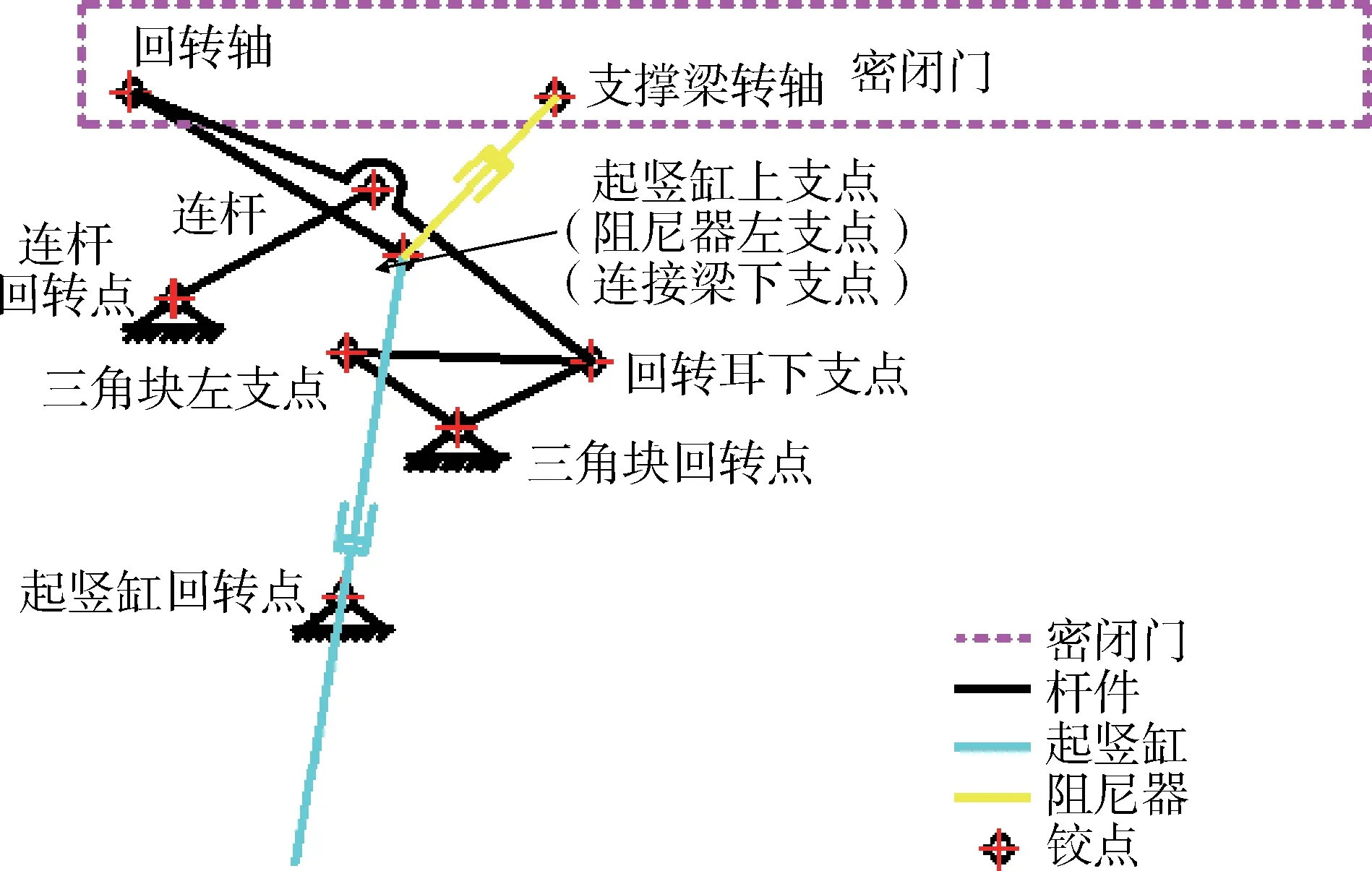
图1 启闭机构布置示意Fig.1 Arrangement of the opening mechanism
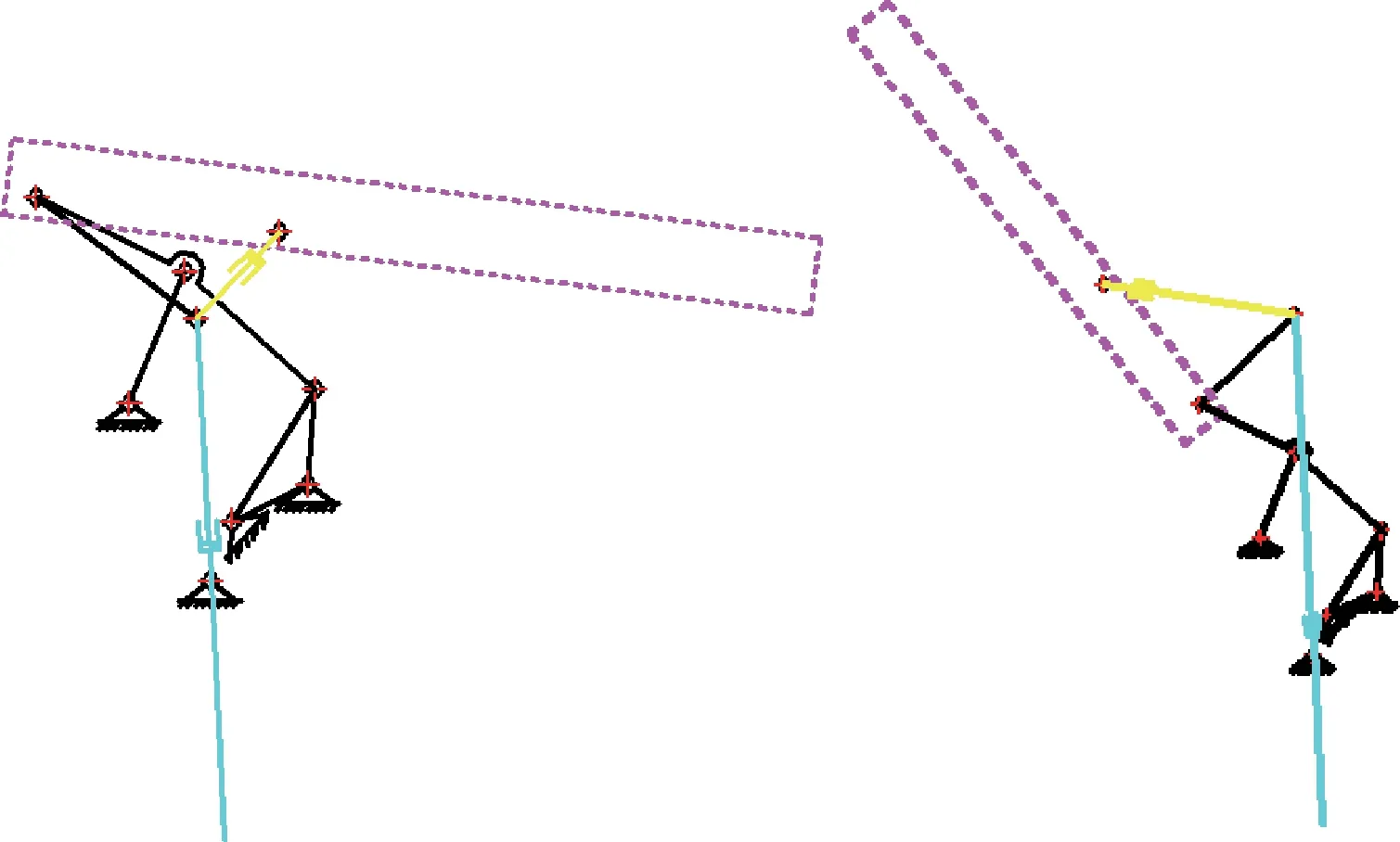
图2 启闭机构动作过程示意Fig.2 The opening process
第二阶段动作主要由起竖缸继续向上伸展实现。此阶段四连杆因三角块左支点已被锁紧器锁死,密闭门在起竖缸向上伸展的作用下绕回转轴转动,阻尼器在密闭门质心过回转轴垂面后开始伸展。
第三阶段动作主要由阻尼器伸展实现,密闭门在惯性作用下继续开启,在达到预定开启角度前阻尼器减速,直至阻尼器伸展开启到位。
1.2 计算分析
依据启闭机构设计原理,建立起动力学理论模型。图3中示意出三角块回转点、回转耳下支点、回转耳中支点、连杆回转点、密闭门回转轴(回转耳上支点/转接梁上支点)。
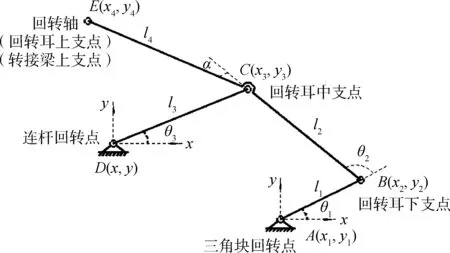
图3 四连杆举升机构示意Fig.3 The four-bar linkage
1.2.1 运动学方程
ABCD四连杆举升机构的运动关系如图3 所示,可得运动学方程组:
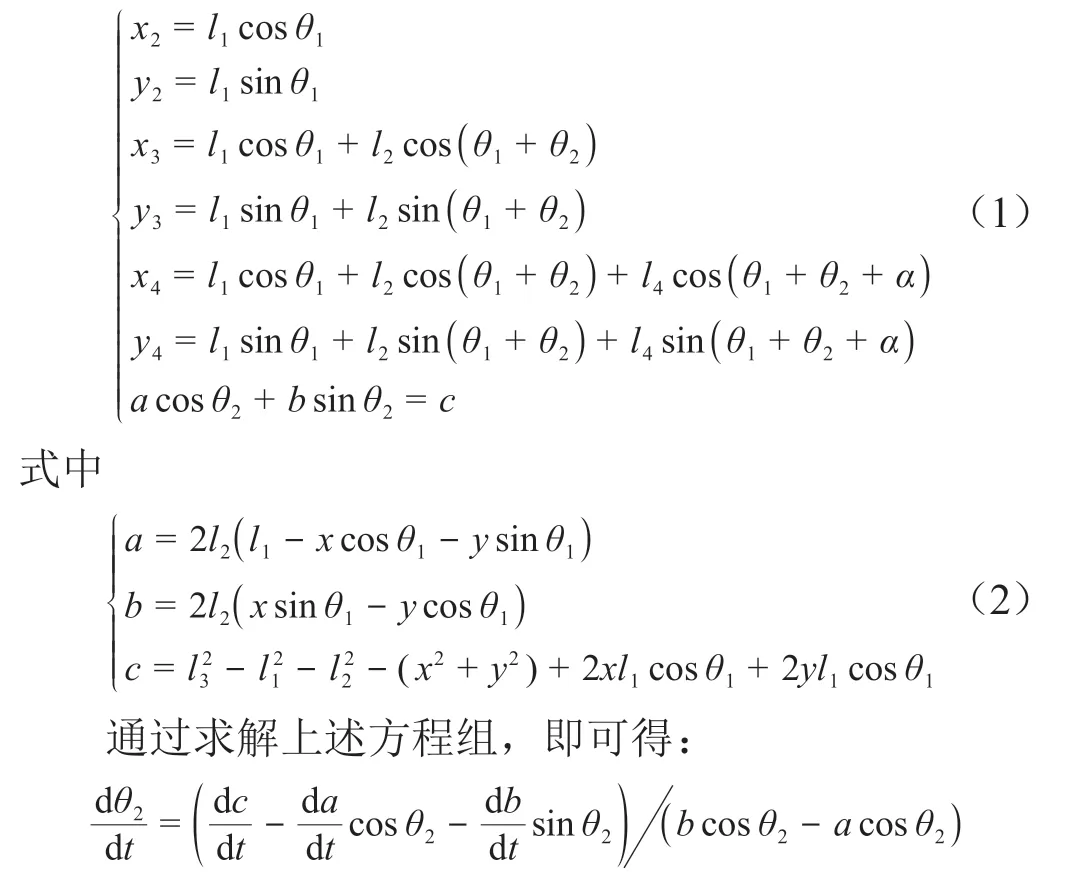
式中
同理可求得四连杆机构其他的运动关系。起竖缸和阻尼器的串联三铰点举升机构的运动学关系较为简单,在此不再赘述。
1.2.2 动力学方程
密闭门回转轴力矩平衡示意如图4所示,因四连杆被锁死,可认为回转轴铰点固支在基座上。
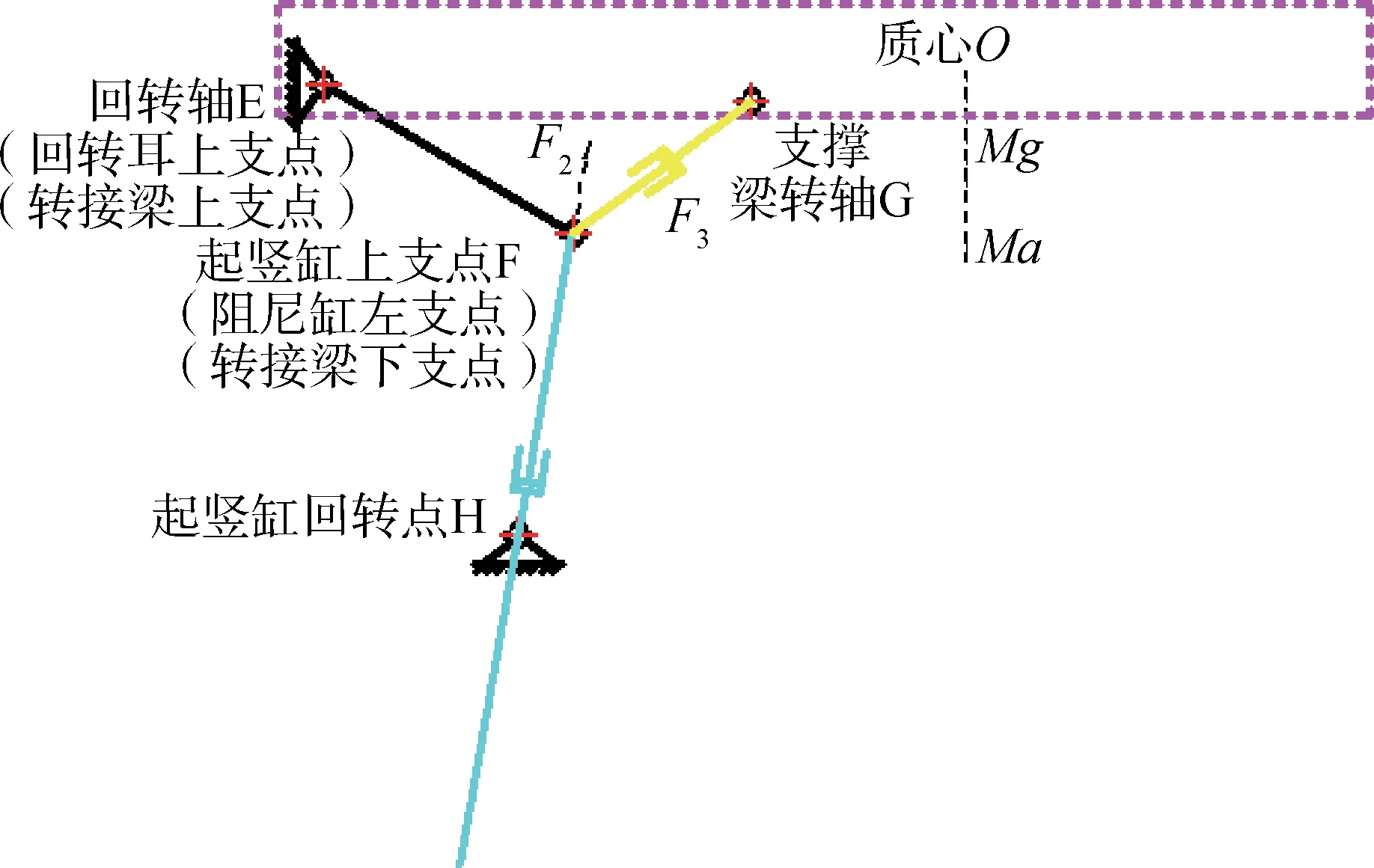
图4 回转轴力矩平衡示意Fig.4 Revolution axis moment-equilibrium
在密闭门的举升和起竖过程中,对密闭门回转点E取力矩平衡,可得平衡方程:
式中F2为起竖缸提供的驱动载荷;M为密闭门质量;g为重力加速度;a为密闭门在开启过程中的加速度;Ma为惯性力矩。
在密闭门的翻转过程中,对密闭门回转点E取力矩平衡,可得平衡方程:
式中F3为阻尼器给密闭门的作用力。
通过耦合求解压力罐启闭机构运动学及动力学方程,即可求得起竖缸和阻尼器的作用力。同样也可求得其它零部件所受到的作用力。
2 多目标优化
对压力罐启闭机构来说,开启时的载荷环境最为恶劣,故在设计油缸等液压系统时,主要根据开启工况载荷分析情况进行设计和选型。同样,启闭机构的结构件也是通过提取开启工作模式下的载荷进行设计。因此本文以开启工况进行动力学多目标优化研究。
2.1 优化目标
考虑使用安全性和便捷性,开启角度不宜太小,但太大的开启角度又对机构和液压缸的承力提出了更高的要求,因此开启角度需要综合多个因素进行匹配和优化。将开启角度作为优化目标,取开启角度的小值,但考虑安全性有一个下限要求,即设置开启角度大于90°作为约束条件,
轻质化、小型化是各类机械结构设计的目标,因此需要减小翻转启闭机构所占空间尺寸。考虑到其纵向尺寸(z轴)取决于各杆件宽度和油缸的外径等参数,优化时暂不做考虑;而垂向(y轴)尺寸涉及到各部件的总体布局问题,仅作约束条件考虑,在进行优化时将整个机构的横向(x轴)尺寸△x作为优化目标。
起竖缸作为启闭机构的主要作动缸,其载荷大小直接影响着动力源及液压系统的选型和布置,故将起竖缸载荷作为优化目标,而其行程仅作为约束条件即可。
综上,优化目标可表示为min [f1,f2,f3],其中f1、f2、f3分别为开启角度、机构横向尺寸△x和起竖缸载荷。
2.2 设计变量
设计变量主要为各连杆的长度和布置角度,对于参数化的模型来说,主要体现在各铰点的x轴和y轴的坐标值。
对各铰点的坐标值优化目标进行灵敏度分析,根据灵敏度分析结果选取铰点A点、D点、E点、F点、H 点的x轴和y轴坐标(以E 点初始位置为坐标原点,水平向右为x轴正方向,竖直向上为y轴正方向)作为设计变量,用数组X表示。
2.3 约束条件
约束条件主要分为两部分:
一是来自功能要求相关方面的约束,主要有:
a)翻转开启角度不少于90°。
b)机构的垂向总长△y不大于2 m。
c)举升阶段回转轴的举升高度为250 mm,此时前端伸出行程不小于85 mm。
d)启闭机构不能超出安装空间边界。
二是主要是来自于诸如结构件和液压系统设计和布置等工程实现方面的约束,主要有:
a)D点需要位于E点的右侧,即xD>xE;
b)开启时起竖缸载荷不超过185 t;
c)起竖缸第二阶段到位后密闭门质心须过密闭门回转轴的垂面;
d)关闭时在密闭门质心通过回转轴的垂面前,起竖缸载荷不超过165 t;
e) 起竖缸行程不大于800 mm。
综上,该翻转启闭机构的铰点优化问题可表示为
式中X为各铰点坐标参数变量;a和b分别为其对应取值边界数组值;f1、f2、f3为优化目标;P为等式约束;Q为不等式约束。
2.4 优化流程
程序设计流程如图5所示。
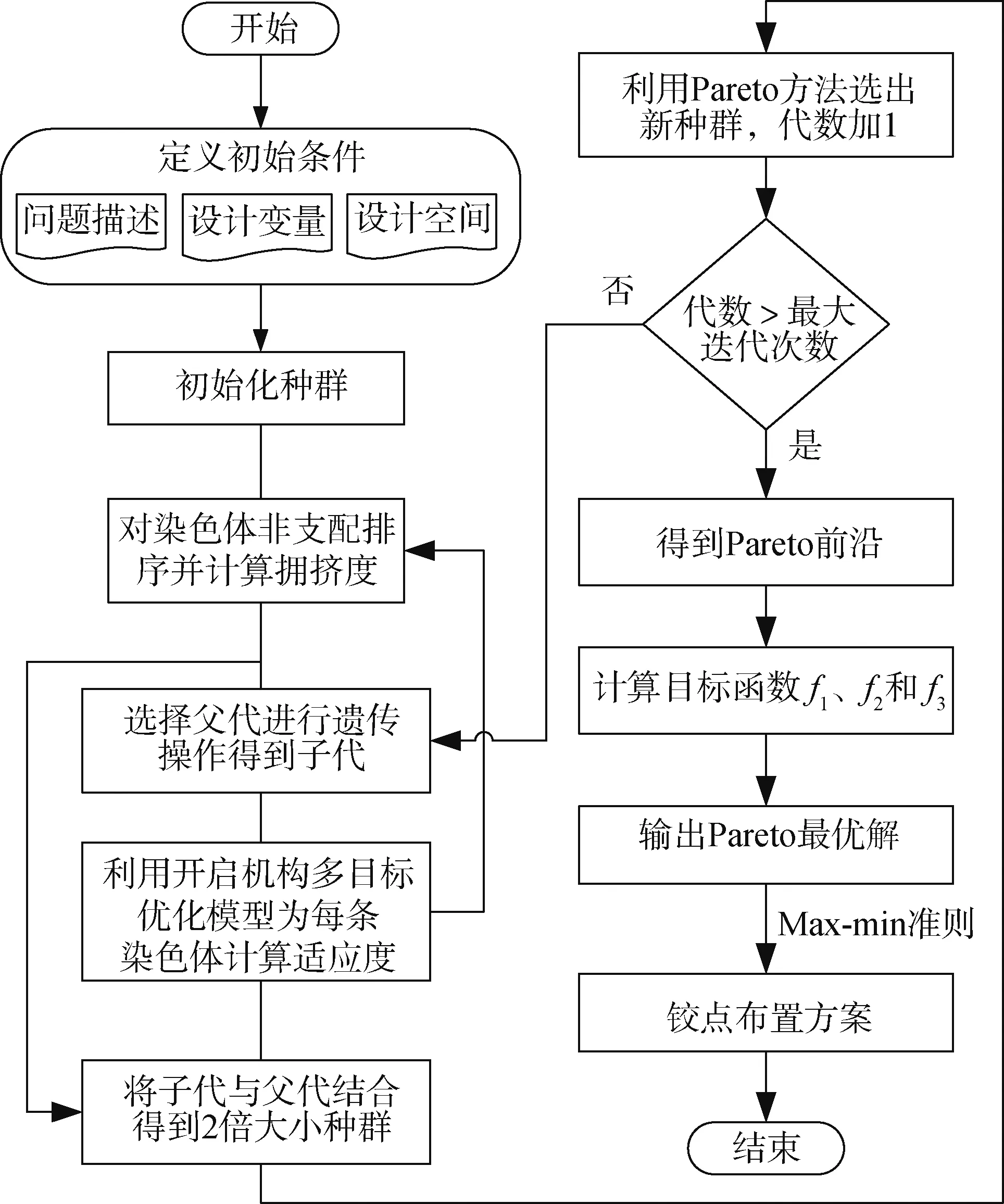
图5 铰点优化流程Fig.5 Flow chart of hinge point optimization
如图5所示,针对上述优化问题,在理论模型的基础上,引入改进的非支配排序遗传算法(NSGA-ⅠⅠ),编制多目标优化程序,即可求得该优化问题的Pareto解,再根据Max-min择优准则[8]即可选得较好的机构铰点布置方案,见式(7)。
2.5 优化结果
根据上述优化流程,优化后启闭机构铰点布局整体方案如图6所示,优化前后铰点位置如表1所示。
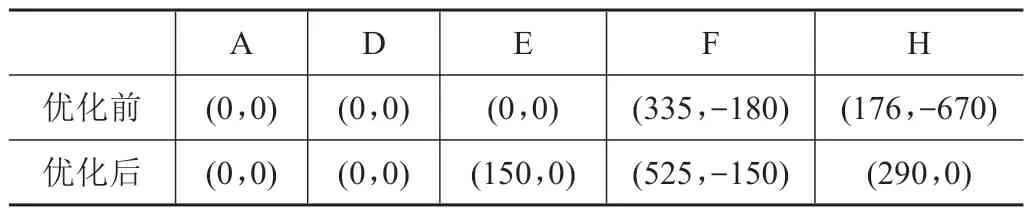
表1 优化前后铰点位置变化情况Tab.1 Position comparsion of before-and-after optimization
同时可以得到,优化前后各优化目标值对比如表2 所示。可以看出,优化后开启角度、横向尺寸、起竖缸载荷分别增大39.2%、减小16.7%、减小29.6%,有效提高了机构性能。
3 试验验证
3.1 仿真验证
为了验证多目标优化方法及优化方案的可行性,根据优化前后铰点布置情况分别进行ADAMS 建模和数值求解计算。因开启角度和横向尺寸与连杆铰点位置、起竖载荷等关联较大,且目前从工程实现角度来说,起竖载荷的大小是影响着开启液压系统设计的关键参数之一,因此以最大起竖载荷为目标进行验证。计算时,采用WSTⅠFF 积分器,SⅠ2 积分格式,进行动力学求解得到起竖缸载荷对比曲线如图7所示。

图7 起竖缸载荷随时间变化曲线Fig.7 Time history plotcomparsion of erecting cylinderloads
由于起竖缸50 s后就已经达到最大行程,之后的受力均由结构限位来承担,因此优化时仅考虑前50 s最大载荷。由图7可知,起竖缸最大载荷由250 t降到175 t,减少了30%,且开启动作全过程中其载荷值也有不同程度的减少。这个结果与之前多目标优化时的理论计算值(176 t)接近,说明了优化方法的有效性。
3.2 样机验证
为了进一步验证翻转机构的设计与优化方案的可行性和有效性,研制了对应样机进行试验验证。5 次试验测试得到折算后的起竖缸平均最大载荷为171 t,这与理论计算值176 t、ADAMS 动力学数值计算值175 t 分别相差2.92%、2.34%,很好地验证了机构设计与优化的可行性和有效性。
4 结 论
本文应用机构功能运动化的步序设计了可变回转点开启结构,构建了参数化机构动力学模型并进行了多目标优化,所得到的优化结果有力地支撑了产品设计。
a)运用多连杆机构时序组合技术,根据机构功能运动化的步序开展了启闭机构总体方案设计,构建了参数化机构动力学模型;
b)以翻转开启角度、机构横向尺寸、起竖缸最大工作载荷为优化目标进行了机构铰点位置多目标优化,并运用Max-min 准则从多目标所得Pareto 解集中选出了折中方案,大大提高了翻转启闭机构性能;
c)通过动力学数值求解计算及样机试验,验证了该启闭机构设计与优化方法的可行性和有效性。

