基于SCA-CHHO-ELM的短期电力负荷预测

库杨杨,王佐勋,刘 健

齐鲁工业大学(山东省科学院) 信息与自动化学院,山东 济南 250353

能源问题渐渐促进了人们消费观念的转变,因此提高能源的利用率以及减少环境污染,是当今社会关注的热门话题。可靠的电力负荷预测方法不仅可以合理配置电力资源以及提高能源的利用率,还有助于维护电力系统的稳定性,电力负荷预测的不准确可能会导致电力公司产生巨大的损失,并且对电网的平稳性造成破坏。因此提高电力负荷预测的精度是电力系统规划的重点研究问题,也有利于为电力部门提供正确的反馈与决策,最终实现电力生产与消耗之间的动态平衡[1-2]。

目前,国内外的专家学者在电力负荷预测这一方向做出了许多成果,尤其是在短期与中期以及长期的负荷预测方面,提出了许多有效的方法,比如趋势外推、人工神经网络、支持向量机(support vector machine,SVM)、极限学习机(extremum learning machine,ELM)等等,这些都是不同发展阶段的经典预测模型,每种模型都有各自的特点,都在不断的被改进。

文献[3]提出了一种结合最小二乘支持向量机(least squares support vector machine,LSSVM) 和基于趋势外推的电力月季比(electricity month-season ratio,EMSR)的混合预测方法,该方法与神经网络与Elman神经网络预测误差进行了比较,结果表明该算法的预测精度有所提高。文献[4]提出了一种用高级小波神经网络预测电力负荷(advanced wavelet neural network,AWNN),先是使用具有熵代价函数的高级小波变换来选择最优小波基,然后用互信息法进行特征选择,最后用BP神经网络进行短期负荷预测,该模型预测结果有较高的可靠性。

文献[5]提出了动态神经网络对日负荷的预测,与该领域广泛使用的传统方法相比,该方法的精度和效率都有所提高。文献[6]提出了一种采用大规模线性规划支持向量机回归模型研究短期电力负荷预测,实验结果表明该方法具有比较小的预测误差。文献[7]提出了一种基于遗传算法的递归支持向量机(recursive support vector machine based on genetic algorithm,RSVMG)来预测电力负荷,使用遗传算法(GA)确定支持向量机的惩罚因子与核参数,实证结果表明,该模型优于SVM模型、人工神经网络模型和回归模型。

极限学习机(ELM)是一种特殊的单隐层神经网络,并且在预测过程中只需要设置输入层参数,输出层参数通过计算得到,具有较为简单的构造,但由于输入层参数的选择对模型的预测精度有一定的影响,因此,研究者们提出了许多方法优化ELM的参数,文献[8]提出了一种用混沌麻雀搜索算法(CSSA)优化并由萤火虫算法(FA)改进的极限学习机(ELM)的初始权重和阈值,首先用混沌策略克服了算法早期局部收敛,然后用萤火虫扰动策略提高算法的全局寻优能力,结果表明,该模型优于其他一些单一模型以及组合预测模型。文献[9]利用PSO算法优化ELM的权重和阈值,但由于PSO算法易陷入局部最优,因此该模型预测效果一般。

由于传统优化算法存在易陷入局部最优的缺点,本文提出了一种基于正余弦扰动的混沌哈里斯鹰算法优化极限学习机(SCA-CHHO-ELM)的预测模型,该算法利用混沌映射产生初始种群,使种群的寻优范围更广、更分散,然后用正余弦策略对个体进行扰动,增强算法跳出局部最优的能力,最后用改进后的哈里斯鹰算法优化极限学习机的权值和阈值就得到了SCA-CHHO-ELM预测模型。我们使用山东某城市的电力负荷数据对该模型的性能进行检验,然后与HHO-ELM、ELM、BP、GRNN的预测效果进行对比,结果表明该模型具有高效的训练过程与较好的鲁棒性,在短期负荷预测方面预测效果比较好。

1 SCA-HHO-ELM模型

1.1 极限学习机

极限学习机(ELM)是一种特殊的神经网络,它只有一个隐含层,其初始权重与偏置是随机确定的,输出层的权重是经过计算得到的。ELM模型的主要计算公式如下。

ELM模型的隐层输出H(x)为:

hi(x)=g(wix+bi),

(1)

其中,x为网络输入,ωi为输入层权重,bi为输入层阈值,g(·) 为激活函数。

ELM网络的输出层输出fL为:

其中,β=[β1,…,βL]Τ为输出层权重矩阵,H(x)=[h1(x),…,hL(x)]为隐层输出矩阵,L为隐层节点数。

极限学习机的输入层的权值和偏置是随机确定的,输出层的权重是在网络训练过程中通过计算得到的,整个过程是在网络的不断迭代中产生最优输入权重与偏置,再利用此基于最优权重的模型预测未来数据[10]。

1.2 哈里斯鹰算法

1.2.1 算法介绍

哈里斯鹰算法(HHO)是近几年新提出的一种群智能优化算法,该算法模仿哈里斯鹰捕食猎物的行为,该行为分为三个阶段,分别为探索阶段、探索与开发阶段和开发阶段[11]。

(1)探索阶段

哈里斯鹰停留在一个位置,然后通过2种不同的策略进行捕猎行为:

其中,X(t)、X(t+1)分别为t时刻与t+1时刻个体的位置,t为迭代次数,Xrand(t) 为随机一个个体的位置,Xrabbt(t) 为猎物在t时刻的位置,即为最优个体位置,r1、r2、r3、r4、q为[0,1]之间的随机数。q为选择将要使用的策略,Xm(t) 为个体平均位置,表达式为:

其中,Xk(t)为种群中第k个个体,M为种群规模。

(2)搜索与开发转换

HHO 算法根据猎物的逃逸能量在全局搜索与局部搜索之间转换,逃逸能量公式为:

其中,E0是为[-1,1]之间的随机数,t为迭代次数,T为最大迭代次数。

(3)开发阶段

根据猎物的实际捕食行为,在开发阶段利用4种位置更新策略对个体位置进行更新。

当0.5≤|E|<1 且r≥0.5 时,采取软围攻策略进行个体位置更新:

X(t+1)=ΔX(t)-E|JXrabbit(t)-X(t)|,

(6)

ΔX(t)=Xrabbit(t)-X(t),

(7)

其中,r是[0,1]之间的随机数,J为[0,2]之间的随机数。

当|E|<0.5,r≥0.5 时,采用硬包围的方式进行个体位置更新:

X(t+1)=Xrabbit(t)-E|ΔX(t)|,

(8)

当0.5≤|E|<1且r<0.5时使用更严密的软包围策略进行位置更新:

Y1=Xrabbit(t)-E|JXrabbit(t)-X1(t)|,

(9)

Z1=Y1+S*LF,

(10)

其中,f(·)为适应度函数,S为n维随机向量,LF为莱维飞行函数的表达式。

当|E|<0.5且r<0.5 时,采取更为严密的硬包围策略进行个体位置更新,更新策略公式如下:

Y2=Xrabbit(t)-E|JXrabbit(t)-Xm(t)|,

(12)

Z2=Y2+S*LF。

(13)

1.2.2 算法步骤

步骤1:种群初始化。根据定义的搜索空间的上界和下界确定每个个体的初始位置。

步骤2:计算初始适应度。计算种群的适应度值,将适应度值最优的个体位置定义为猎物位置。

步骤3:位置更新。计算个体的逃逸能量,根据能量与生成的随机数选择不同策略对猎物的位置进行更新。

步骤4:更新个体位置与适应度。计算新的适应度值,判断是否优于个体当前适应度值,如果优于当前适应度值,则用新的个体位置与适应度值代替当前个体位置与适应度值,反之,个体位置与适应度不变。

1.3 基于SCA的CHHO算法

为了提高HHO的跳出局部最优能力以及寻优精度,提出了一种基于正余弦扰动策略的混沌哈里斯鹰算法。

1.3.1 Tent混沌映射

由于Tent映射具有遍布均匀性、随机性的特点,因此我们利用Tent混沌映射策略初始化种群,让初始种群位置均匀遍历在搜索空间中,来提高算法跳出局部最优的能力。

1.3.2 正余弦扰动策略

正余弦算法(SCA)是一种新的优化算法,主要通过正弦函数与余弦函数进行位置更新,它具有寻优性能好、结构简单、易于实现的特点。利用该算法在HHO每次迭代后进行位置扰动,来克服算法易陷入局部最优的缺点,表达式为:

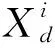
1.3.3 基于SCA的CHHO算法步骤

步骤1:种群初始化。根据搜索空间的上界和下界,利用Tent映射产生种群的初始位置。

步骤2:计算初始适应度。计算每个个体的适应度值,将最优适应度的个体位置定义为猎物位置。

步骤3:位置更新。计算个体的逃逸能量,根据能量与生成的随机数选择不同策略对猎物的位置进行更新。

步骤4:更新适应度。用正余弦扰动策略来更新当前最优位置,计算新的适应度值,判断是否优于个体当前适应度值,如果优于当前适应度值,则用新的个体位置与适应度值代替当前个体位置与适应度值,反之,个体位置与适应度不变。

SCA-CHHO算法的具体流程如图1所示。

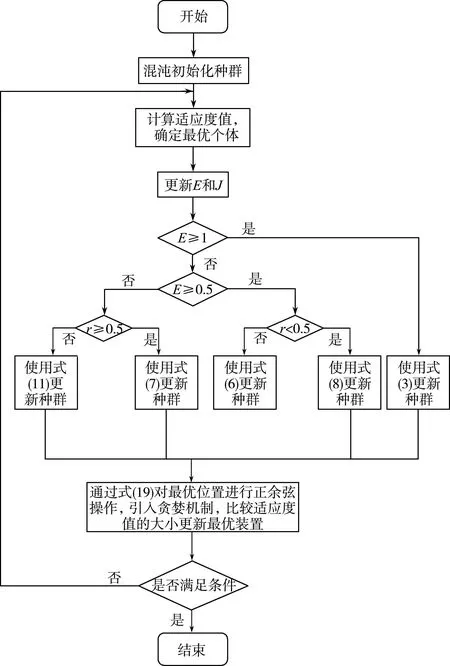
图1 SCA-CHHO流程图

1.4 基于SCA-CHHO-ELM负荷预测模型的建立

SCA-CHHO-ELM算法流程图如图2所示。SCA-CHHO-ELM网络分为改进哈里斯鹰算法模块和ELM网络模块两大部分。

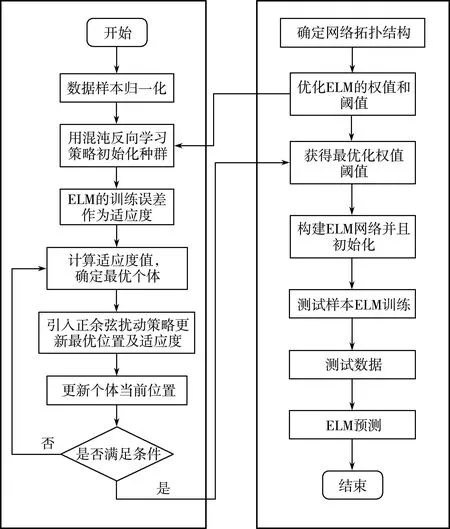
图2 SCA-CHHO-ELM预测模型

1.5 预测模型输入输出的选取

电力负荷由于具有一定的变化规律,而且也受到气温、时间等因素的影响,所以我们在进行负荷预测时要考虑到负荷自身的属性以及其他重要因素的影响是得到准确预测结果的关键。

由电力负荷特性分析得到,负荷按照日或周有规律的波动,并且还会受到气温因素的影响。所以在本文的预测模型中我们需要考虑负荷的日周期性,还要充分利用影响负荷变化的各种因素,如平均温度,湿度,降水量以及日期类型等。我们将1 d的时间划分为24个点,平均1 h取一个负荷数据,以历史数据中相同周以及相同小时作为输入量,以预测日当天的对应的小时作为输出量对网络进行训练预测。具体内容如表1和表2所示。

表1 网络模型输入量

表2 网络模型输出量

该数据来自于山东省某城市2013—2014年的负荷数据,我们选取4月1日—4月19日每日24个测量点作为训练集,选取4月20日当天24个测量点作为测试集。由于异常值与缺失值会影响预测结果,需要先对数据进行预处理。对于缺失值采用前后2 d的平均值来补齐,对于异常值判断它与相邻时刻的百分误差是否超出10%,如果超出就用对它进行插值处理。

2 实验结果分析

本文采用了均方根误差与平均绝对百分比误差作为负荷预测精度的评价指标。

为了检验所提出模型的可靠性,选用了单一的ELM预测模型与标准的HHO-ELM和提出的模型进行对比,如图3所示。

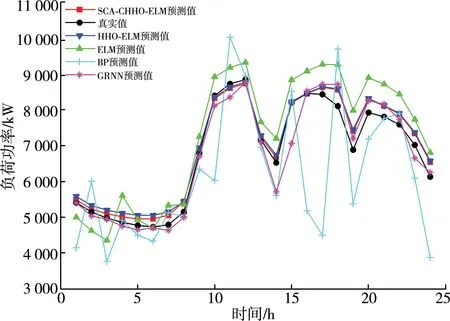
图3 预测值与真实值的对比图

图3横坐标表示1 d的24 h,纵坐标表示电网的用电负荷功率。结果表明,所提出的模型相比于其他模型预测效果更好,SCA-CHHO-ELM相比于HHO-ELM的稳定性更好,说明SCA-CHHO大大提高了HHO的寻优能力,SCA-HHO-ELM的预测效果也明显优于其他对比模型,进一步说明了所提出的预测模型在短期负荷预测方面具有准确的预测精度。

本文引入了均方根误差与平均绝对百分比误差作为模型的预测效果的评价标准,其对比如表3所示。

表3 3种模型的预测值与真实值的百分比误差

由表3看出,SCA-CHHO-ELM的RMSE相比于其他模型提高的最大值和最小值分别为0.47%和0.02%,SCA-CHHO-ELM的RMSE相比于其他模型提高的最大值和最小值分别为0.47%和10.97%,模型精度的提高十分明显,再次表明了所提出的预测模型的预测精度优于其他预测模型,在短期负荷预测中效果十分显著。

3 结 论

本文主要研究了短期负荷预测的方法,提出了SCA-CHHO-ELM模型,其结论如下:

(1)它提高了HHO算法全局寻优的能力。用正余弦扰动策略对HHO算法每一次迭代结果进行扰动,防止陷入局部最优,使所得到的ELM的权值与阈值更佳,最终大大提高了ELM的预测精度。

(2)SCA-CHHO-ELM模型在短期负荷预测方面效果良好。它与HHO-ELM和ELM、BP、GRNN的预测结果进行对比具有更好的预测精度与泛化能力。