引力理论框架下基于综合竞争力的自动驾驶拟人换道决策模型

裴玉龙，傅博涵，王子奇，张杰,2

(1.东北林业大学，土木与交通学院，哈尔滨 150040；2.宁德师范学院，信息与机电工程学院，福建宁德 352100)

0 引言

智能网联自动驾驶车辆(Connected-automated Vehicle,CAV) 和人工驾驶车辆(Human-driving Vehicle,HV)的区别在于对于周围信息感知的全面性和决策与执行的即时性，相比于传统的HV，CAV对安全距离和可接受换道间隙等的判断依据不同，可以在更苛刻的条件下做出合理的换道决策，还可以通过实时信息交流与周边车辆实现协同换道策略，并且使其换道行为对交通运行效率的影响降到最低。未来CAV 的市场渗透率将持续升高，换道决策是自动驾驶行为决策中极其重要的一部分，也是交通领域的研究热点之一，故研究智能网联环境下车辆的换道决策十分必要。

近年来，基于力场、势场、分子动力学及机器学习等相关理论的模型及构建方法推广至交通研究领域，并取得了一定的研究成果。秦雅琴等[1]采用社会力模型研究事故瓶颈影响下的换道决策行为。考虑到车流中系统的相似性，曲大义等[2]将微观车辆比作分子，基于分子动力学理论及动态影响因素建立分子动力学换道模型，更客观地展现自动驾驶车辆的换道行为特性。利用深度学习方式进行换道决策模型的构建也是当今研究的热点之一，基于规则与机器学习融合[3]和贝叶斯优化算法[4]的车辆换道决策模型，通常以提升决策准确度和识别率为目标，通过决策树提取换道特征和规则，实现换道决策的预测。

驾驶风格和换道行为的产生具有必要的联系。冯焕焕等[5]提出引入驾驶风格的熵权法多属性换道决策模型，发现普遍存在激进型驾驶风格平均换道概率最大和保守型驾驶风格平均换道概率最小的现象。吕超等[6]针对超车过程中主车和被超越车之间的交互行为，引入心理学中的“社会偏好”描述被超车的纵向特征，并将其融入基于强化学习的自主超车决策系统设计中，提升了决策的自适应性和合理性。

车辆的微观特性服务于中观及宏观的车流状态，而换道行为研究的重点在于车辆的交互行为及换道车辆对其他车辆的影响，可将换道模型分为利己性换道模型和利他性换道模型，前者更加关注换道车辆本身的状态，强调换道后自身收益大小，杨达等[7]考虑创建主车感知范围内多项指标的成本函数，以行车收益最大化为目标输出最优车道序列，以Gipps 模型为基础构建安全条件判断模型，筛选最优车道，模型安全性较高；后者更关注与其他车的交互对整体交通效率的影响。驾驶员在换道过程中，存在各种主观不确定因素，模糊逻辑推理可有效描述无法用准确模型表示的模糊概念，有研究人员基于建立模糊规则[8]，结合多车交互推演将目标车辆与本车间的预测距离作为输入，通过模糊逻辑决策输出换道概率，预测周围其他车辆的运动趋势。考虑车辆换道后对原车道与目标车道多辆后随车制动影响程度的不同，潘义勇[9]构建加权整体制动最小化换道模型(Minimizing Overall Braking Induced by Lane Changes,MOBIL)，相对传统模型而言，提高了交通流的平均速度，减少了整体的制动幅度，有效提高交通流的运行效率及安全性。

现有研究关于换道决策行为的研究中，对于交互的复杂性描述和量化尚不清晰，大多仅考虑主车和相邻车道车辆的简单场景，忽略了相邻及相隔车道上车辆可能产生的换道和加减速行为对主车换道决策的影响，即缺乏对于车辆实施换道决策后车辆之间未来可能产生的竞争行为对驾驶人换道决策的影响分析。本文在深入研究自动驾驶换道决策的基础上，从真实轨迹数据出发，基于悲观主义原则量化分析可能产生的竞争行为，同时，考虑驾驶风格异质性，模拟人类驾驶员换道决策心理，综合考虑换道意愿、竞争行为和换道后环境对主车换道决策的影响，提出引力框架下的换道决策模型，为自动驾驶车辆做出更准确的换道决策提供参考。

1 车辆换道意愿分析

1.1 换道环境构建

CAV 与HV 混合驾驶的道路环境中，HV 表现出相对独立的特性，车辆由驾驶人控制，环境与车辆的信息通过驾驶人视觉作为中介进行传递，这种传递具有延时性，具体表现为驾驶人为应对周围环境变化产生的反应时间和信息处理所需要的决策时间相对较长，而且驾驶人仅能凭借周边车辆和标志标线等的变化判断下一步行为，不能像自动驾驶车辆那样在短时内感知和预测驾驶人视觉盲区外各车辆的状态并做出实时反馈和合理决策。

由于影响到车辆换道决策的车辆位置、车辆类型及驾驶风格等因素描述较为冗余且复杂，为辨别换道车辆周边不同类型车辆的属性，定义车辆Ci是由位置属性(紧邻前方左侧车辆、紧邻正前方车辆、紧邻前方右侧车辆、左侧相隔车道平行车辆、右侧相隔车道平行车辆、紧邻后方左侧车辆及紧邻后方右侧车辆)、车辆状态(系统接管的CAV状态与人类接管的类HV 状态)和驾驶风格属性(普通型、常规型和冒险型)构成的交通个体。考虑道路上普遍存在的换道场景，建立单向5 车道换道环境如图1所示，其中，M 为主车，编号i=1,2,…,7 分别为主车行驶方向左前方车辆、正前方车辆、右前方车辆、左后方车辆、右后方车辆、左侧相隔车道车辆及右侧相隔车道车辆，在实际分析中，将与M 纵向车头间距±10 m内的相隔左侧车道车辆视为C6，相隔右侧车辆视为C7。为便于后续分析主车左侧和右侧环境，将主车左侧车辆编号i=1,4,6 所组成的环境称作“车辆组L”，将主车前方车辆编号为i=1,2,3所组成的环境称作“车辆组S”，将主车右侧车辆编号为i=3,5,7 所组成的环境称作“车辆组R”，N 表示组外车辆，即与M 换道决策无关的车辆。

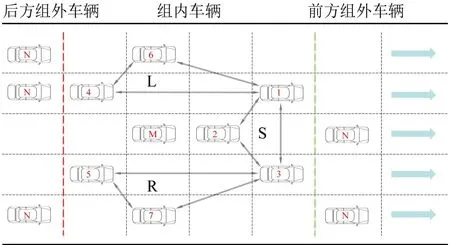
图1 传统换道场景Fig.1 Traditional lane changing scenario

1.2 换道意愿属性

换道过程包括意图产生、换道决策和换道实施这3个过程，而换道意图是换道决策的重要依据之一，换道意愿是换道意图的量化，表示换道意图的强度。车流密度相对低的交通环境中，左侧车道的车速比右侧车道快，对于驾驶人来说，向左换道后产生的舒适性收益和速度收益比向右换道高，驾驶人倾向于左侧车道行驶导致向左换道的驾驶行为多发；在高密度交通流、临近交叉口及临近交织区出口等驾驶人面临选择的区域内，车流速度、车头时距及车头间距较小，车、路及环境等因素对车辆换道决策的干扰性强，驾驶策略的产生往往是被动的，常产生强制性换道行为；本文涉及交通流环境为中等密度交通流，混合着强制性换道行为和非强制换道行为，各车道车流速度差距小，在换道决策上不存在左右侧速度收益差距过大的情况，故在换道意图量化上不考虑向左换道的偏向性。

类似于驾驶人在限制视角范围内接收外界信息，CAV 通过雷达或摄像头获取前方车辆信息，故主车换道意愿由前方车辆属性决定，相关属性如下。

(1)邻近前车相对速度

车辆未达到驾驶人期望速度，且相邻车道紧邻前车速度较本车道前车速度高时，驾驶人产生换道意图，故将邻近前车相对速度ΔvCi-M作为换道意愿属性，即

式中：vCi为主车M 周边车辆Ci的速度，当i∈[1,3]时，vCi表示邻近前车速度；vM为主车M 的速度。

(2)邻近前车车头间距

主车M 与当前车道前方车辆的车头间距小于M 与相邻车道紧邻前方车辆的车头间距时，驾驶人可能产生换道意图。车头间距dCi-M为主车与周边车辆之间的车头纵向距离，即

式中：dM为主车M 当前所在位置；dCi,i∈[1,3] 为邻近前方车辆位置。

(3)驾驶风格

BERDOULAT等[10]发现，频繁换道、鲁莽换道及近距离跟驰等驾驶模式发生的频率是激进驾驶的显著表征，故不同的驾驶风格对换道决策存在一定影响。考虑实际交通运行场景中车辆的驾驶风格Td,M的不同，分类标签数量的增加会使分类的解释变得复杂，现有研究普遍将驾驶风格归结为激进、适度和保守这3 种类型，因此，以此3 种类型作为驾驶风格的主要分类依据。将驾驶风格的量化表达为

式中：d 为驾驶人，表示驾驶风格的拟人化性质。

1.3 换道意愿量化表征

由于换道意愿的模型计算涉及主车换道意愿属性，其中，包括前后车车头间距和相对速度，而在实际换道场景下，常常会出现前方3车道部分车道或全部车道没有行驶车辆的现象，此时，无法在模型中通过车头间距和相对速度量化主车换道意愿，为方便模型的计算且对结果不产生影响，在图1所示相应位置缺失车辆时引入虚拟单元，虚拟单元1、单元2及单元3是假设存在，在实际中是不存在的，将其与主车的纵向间距设为协作换道行为接受间隙的最大值30 m[11]，即至少可以保证车辆从容换道的临界距离；虚拟单元速度为快速路交织区限速80 km·h-1，具体设置值可根据所在路段限速值进行调节，这规定了主车换道后可实现的最大车速。

复杂环境下，采用前方车辆与主车的速度属性和位置属性反映主车的换道意愿，表征方式为

式中：GD=(⋅∙)为主车M 产生换道意图时，在行车环境中的换道意愿表征函数；lead 为换道意愿量化依据的是前方车辆属性；TM为主车M 的类型，指驾驶风格Td,M；D∈{l,r} 分别为向左和向右的换道意图。

随着目标车道紧邻前车与主车的车头间距和速度差的增大，驾驶人对于该目标车道的意愿增加，且增加值相对于速度量纲变化较小，故直接采用间距作为模型的一部分，当前后车速度差超过阈值时，驾驶人对目标车道的速度期望易达到满足，速度差对驾驶人换道决策的影响逐渐趋于稳定，模型使用tanh 函数对速度差进行范围约束，同时，降低最终的计算成本，由于驾驶人做出决策最直接的判断方法是紧邻前车与主车之间的距离，而驾驶人的期望间距随驾驶风格而改变，故在模型内对间距施加驾驶风格的影响，即

式中：τ为期望速度修正系数；γ为期望间距修正系数。

2 换道竞争行为分析

2.1 悲观主义原则下的潜在竞争强度定义

传统换道过程分为自由换道、协作换道和强制换道这3 种，现有研究中，车辆协作行为的定义多是指主车通过多次发出换道请求直到后车接受，若后车接受换道请求，则会实施减速和匀速等协作行为，为主车提供成功换道的条件，若后车拒绝对方换道请求，则采取加速或者匀速等竞争策略。在我国，受周围环境、社会文化以及自身道德水平等多方面因素影响，驾驶人多采用竞争式驾驶行为，与发达国家的协作式通行行为存在显著差异。驾驶人在实施换道行为时，要考虑前车和后车间距，保证换道后主车和跟随车均能安全跟驰。

由上述分析，考虑通过驾驶风格差异和车头间距比引入“潜在竞争强度”的概念。潜在竞争强度是主车产生换道意愿时，在与周边车辆产生竞争行为的情况中其换道优势的量化。潜在竞争强度的概念建立在悲观主义准则(最大最小准则)的基础上，即考虑主车周边的车辆与其产生竞争行为的“最坏”情况下，建立的模型并选择最优决策，体现了保守决策原则，即

式中：(⋅)为主车M 与车辆Ci的潜在竞争强度函数；fgap为产生竞争行为时，关于车头间距的反正切函数；∂为间距修正系数；β为驾驶风格修正系数；ΔTd,M-Ci为驾驶风格差异；treact为决策干预因子。对潜在竞争强度表达式的相关属性解释如下。

(1)车头间距比

以指定车辆间的车头间距比衡量主车的换道优势，假定主车与对比车辆在相同区域存在竞争关系时，拥有更好间距条件的车辆在竞争区域的占据上更有优势，车头间距为式(2)。

(2)决策干预因子

引入决策干预因子使CAV 能够在恰当的时候人为实现非接管状态下决策的干预，避免人类接管行为的不确定性。treact为决策干预因子，不干预状态下默认驾驶风格为常规型(Td,M=0.5)；干预状态下，可设定人类喜爱的驾驶风格Td,M进行决策干预调节。

由于拟人化决策模型采用人类驾驶数据反映驾驶风格，故本文模型在初步确立的过程中采用轨迹数据确认驾驶风格，即视为人类干预状态。参数标定后的模型在实际应用中可通过决策干预因子调整CAV驾驶风格。

(3)驾驶风格差异

CAV 决策系统引入符合人类习惯的驾驶风格参数实现拟人化，驾驶风格越激进，驾驶人更倾向于频繁换道，且对车辆的横向控制稳定性越差，所以，在执行换道行为前后对周边车辆产生较大的威胁，融合决策干预因子后的驾驶风格差异量化为

式中：Td,M为M 车的驾驶风格；Td,Ci为Ci车的驾驶风格。ΔTd,M-Ci>0 时，M 车比Ci车相对激进，M 车倾向于竞争位置；ΔTd,M-Ci<0 时，M 车比Ci驾驶人保守，M 车倾向于让出位置。

2.2 基于潜在竞争强度的换道竞争行为分析

(1) M 与C6的潜在竞争强度

当M 和C6均发起向中间车道同一目标间隙的换道请求时，若中间车道仅能满足其中一辆车的最小可接受间隙，则仅有一辆车可以成功换道，如图2所示。由于本文不考虑换道环境外其他车辆对环境内车辆(包括主车及其周边7辆车)的影响，同时，为降低模型的复杂性，引入虚拟单元Cf表示C6当前车道前方车辆，并假设Cf与C1纵向位置相同，即dCf=dC1。当C6所在车道前车Cf与C6的车头间距越大，M 所在车道前车C2与M 的车头间距越小时，M 相对于C6具有较强的竞争性。同样，考虑驾驶人风格，驾驶人的激进程度对竞争强度产生正反馈效果。故M 与C6存在该位置关系时的潜在竞争强度为

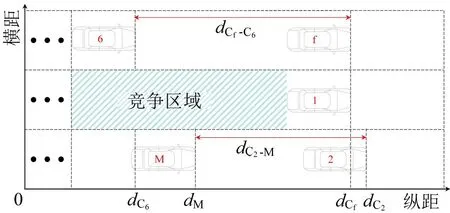
图2 M 与C6 的竞争关系Fig.2 Competitive relationship between M and C6

(2) M 与C4的潜在竞争强度

M 向左换道时，会占据C4前方空隙，若换道条件不充分，例如，C1与C4间隙小于M 所能接受的最小换道间隙，M 会向C4发起换道请求，若C4不同意换道请求，则会保持原速或加速，与M 形成竞争关系，如图3所示。M 与C2的车头间距越小，与C4的车头间距越大，M 的换道可能性越高，潜在竞争强度越高，驾驶员越激进，其竞争成功性越强，故M 与C4存在位置关系时的潜在竞争强度为

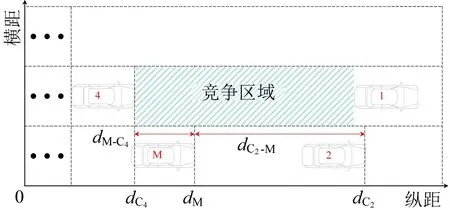
图3 M 与C4 的竞争关系Fig.3 Competitive relationship between M and C4

(3) M 与C1的潜在竞争强度

M 和C1存在两种竞争行为，一种是，M 向左换道与C1的竞争，M 与C2的车头间距越小，M 与C1的车头间距越大时，M 向左换道的可能性越高，潜在竞争强度越高；另一种是，M 加速时与向右换道的C1产生的竞争，当C1因前方组外车辆N 而产生向右换道决策时，则会产生和M 争抢前方空隙(竞争区域2)的竞争行为，如图4所示，M 与C1存在位置关系时的潜在竞争强度如下。

图4 M 与C1 的竞争关系Fig.4 Competitive relationship between M and C1

向左换道为

保持车道为

(4) M 与C2的潜在竞争强度

若C2和M 两者同时存在向左换道倾向，且C1与C4的间隙小于M 与C2同时换道所需要的最小换道间隙(竞争区域2)时，两者仅有一辆可成功换道，存在竞争关系，此时，C2的换道选择影响着M的换道决策，M 比C2激进时，M 更有可能争抢到换道机会，本文未考虑协同换道，故不将M 与C2存在的换道竞争强度纳入计算中。如图5所示，当C2存在向左或向右换道倾向时，会为M 前方留出空隙(竞争区域1)使M 向前补充，C2比M 激进时，C2换道及加速的可能性越高，此时，M 向前加速保持车道的可能性增加，故M 与C2存在位置关系时的潜在竞争强度为

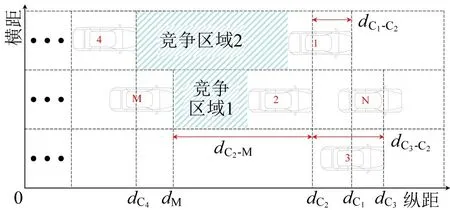
图5 M 与C2 的竞争关系Fig.5 Competitive relationship between M and C2

(5) M 与其他车辆的潜在竞争强度

CAV通过感知端获取周边车辆运行信息，不考虑驾驶位置对驾驶人判断和操作的影响，故采用对称式换道分析方法，M 与左侧车辆和右侧车辆的竞争存在如图1所示的对称关系，将其用符号表示为⊗，例如，M ⊗C3表示M 与C3之间的竞争关系，等价关系为

对于潜在竞争强度的计算，作出以下说明：M周边车辆存在如图1所示位置关系时，则将潜在竞争强度纳入考虑；相应位置不存在车辆时，不纳入潜在竞争强度计算。

3 换道决策模型构建

3.1 引力理论框架下的竞争力表征

在引力与质量成正比，与距离成反比的理论框架上，应用竞争力与换道决策下的综合竞争强度和保持车道决策下的综合竞争强度成正比，与换道后的环境稳定性成反比的关系，构建基于引力理论的竞争力为

式中：FD为对应D决策下的竞争力，D∈{l,r} ；GD为换道意愿；mD为向左和向右换道决策的综合竞争强度；mk为保持车道的综合竞争强度；?为速度“伪距”，v表示速度；为加速度“伪距”，a表示加速度。具体属性解释如下。

(1)换道意愿——等效引力常量

换道意愿是判断是否换道的依据，涉及保持车道、向左换道和向右换道这3种决策的综合竞争强度模型均与前方车辆的潜在交互行为有关，说明M很大程度受到来自前方车辆的影响，所构建的模型符合实际。向左或向右两种换道决策所依据的换道意愿等值，其大小视当时前方车辆的状态决定，故视为等效引力常量，表达式为式(5)。

(2)综合竞争强度——等效质量

综合竞争强度是执行不同决策后，主车与其他车辆间的潜在竞争强度之和，分别包括向左换道D=l、向右换道D=r 和保持车道D=k 这3 种决策下的综合竞争强度，即

如图1 所示，D=l 时，综合竞争强度的计算对象为车辆组L 内的车辆1、车辆4 及车辆6；D=r时，综合竞争强度的计算对象为车辆组R 内的车辆3、车辆5 及车辆7；D=k 时，综合竞争强度的计算对象为车辆组K 内的车辆1、车辆2及车辆3。

(3)速度“伪距”与加速度“伪距”——等效距离

周边车辆的运行状态及趋势决定着M 执行换道决策后的行驶环境，LEE等[12]通过实际车辆变道数据的采集与分析表明，接近95%的驾驶人会因车辆频繁加减速而产生不舒适感，故换道决策还应考虑换道前后车内人员的舒适感，同时，考虑到自动驾驶环境下CAV比例的增加有利于交通流稳定性的提升。本文引入速度“伪距”和加速度“伪距”，采用M 周边各车辆纵向上加速度和速度的离散程度，以表征周边车辆的运动波动程度，波动程度越大，主车M 选择换道后环境相对于保持车道所处环境的不稳定性越大，乘员舒适性越低，即

式中：ai为车辆Ci在M 产生换道决策时的瞬时纵向加速度；vi为车辆Ci在M 产生换道决策时的瞬时纵向速度；ND为各决策下，对应车辆组中的车辆个数，Nl、Nr分别为M 左侧和右侧车辆个数；D为各决策下，对应车辆组内的车辆纵向加速度平均值；

3.2 基于综合竞争力的换道决策模型

综合竞争力FM是两种决策下竞争力的合力，规定向左决策的竞争力方向为正。当FM>0 时，向左换道决策的综合竞争强度产生的竞争力大于向右换道决策的综合竞争强度产生的竞争力，此时，M 更倾向于向左换道；当FM<0 时，向右换道决策的综合竞争强度产生的竞争力大于向左换道决策的综合竞争强度产生的竞争力，M 更倾向于向右换道。

式中：Fl为向左换道决策下所产生的竞争力；Fr为向右换道决策下所产生的竞争力。

力是改变物体运动状态的原因，车辆短期内的运动状态变化反映了决策的结果，初步考虑用速度或加速度作为决策判断结果的参考，但由于数据采集精度及数据处理的影响，需要对横向距离-时间曲线求导，并进行降噪处理得到横向速度和横向加速度随时间变化的曲线图，相对于横向加速度而言，横向速度数据降噪后的精度损失较小，故采用横向速度作为模型求解目标。M 受综合竞争力FM作用下产生的横向加速度lateral为

主车在换道决策阶段仍保持当前车道行驶，故视为横向初速度为0 m·s-1，为降低计算成本，假设主车换道过程中横向速度均匀变化，在2 s 内达到最大横向速度，在换道判断上采取横向速度采样时段2 s 内的横向速度均值为求解目标，故横向速度M为

式中：tsample为采样时间段，取2 s；v0为横向初速度，取0 m·s-1；vmax为换道过程中最大横向速度。

综上，模型求解目标值横向速度为

模型输入-输出如图6所示。

4 模型参数标定

4.1 数据准备

拟人化自动驾驶决策模型是基于人类驾驶数据进行模型训练的，本文所用轨迹数据集为东南大学UTE(Ubiquitous Traffic Eyes)开源数据集[13]中的KZM5数据集，数据集车辆识别精度100%，研究路段长度140 m，双向10 车道，采集视频覆盖100 m的双向交织区，如图7 所示。车辆轨迹数据库包括：车辆编号、位置坐标、车道编号、车辆长度、车辆宽度、行驶速度、车头时距、车头间距及加减速度等字段，时间精度为0.03 s，满足研究需求。

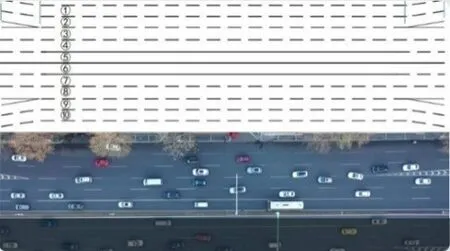
图7 KZM5数据集无人机拍摄区域Fig.7 Area photographed by drone in KZM5 dataset

数据集中，车流密度相对适中，换道行为的发生具有普遍且较强的典型特性，能够精确地表征车辆换道情况下的微观驾驶行为，可以为换道决策模型的标定提供良好的数据基础。由于初始数据(原始数据结构如表1 所示)直接反映车辆的动力学参数和空间参数，而且包含除换道行为外的数据，所以，需要对原始数据进行预处理工作。数据处理步骤如下：

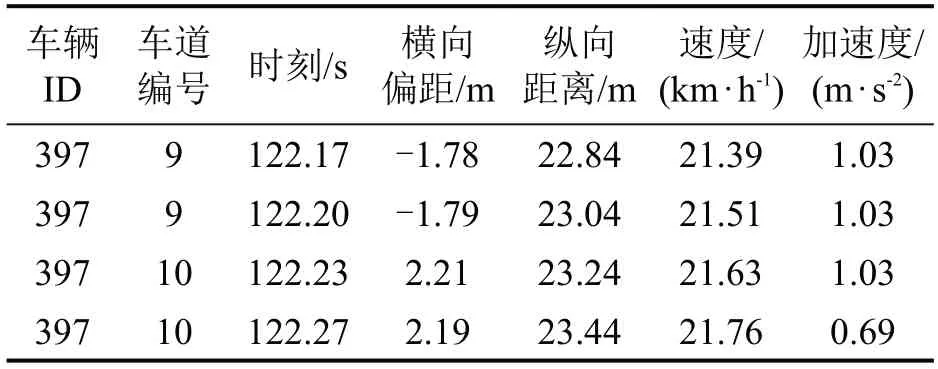
表1 原始车辆数据Table 1 Original vehicle data

(1)筛选样本

记录同一车辆编号的位置坐标及车道编号发生变化的时刻，且变化后车辆的速度、加速度以及稳定时间符合上述要求，记为换道行为样本，筛选样本数据结构如表2所示。通过人工筛选得到113辆换道车的124 条换道样本。

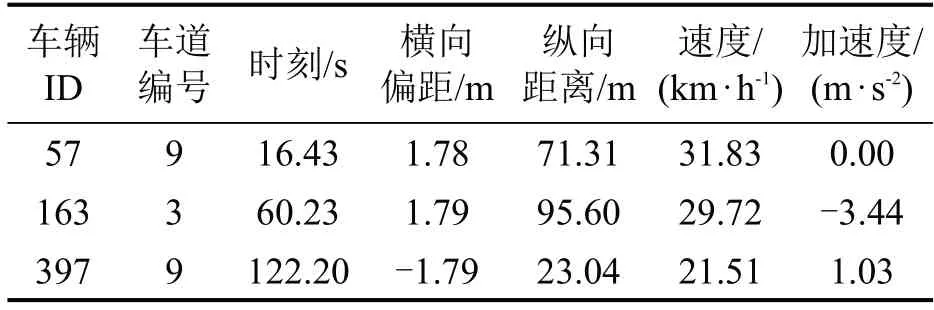
表2 换道车辆数据Table 2 Data on lane-changing vehicles

(2)决策时刻数据提取

选取换道行为样本中各车辆编号在车道变化前一采样时刻，向前以2 s时间窗进行平移[14]，并将平移后所在时刻作为换道决策事件开始帧，并记录该采样时刻周边车辆的车速、加速度以及车辆位置，车辆组数据结构如表3 所示。在处理过程中，周边车辆在主车换道决策同一时刻下有部分数据缺失的现象，针对此问题，采取视频观测结合浮动取值的方法，即以采样精度为时间窗长度，以初始换道决策事件开始帧为起点，向该时刻前后平移时间窗，并按平移后时刻进行视频观测和数据表核查，保证换道决策时刻下的数据完整性。

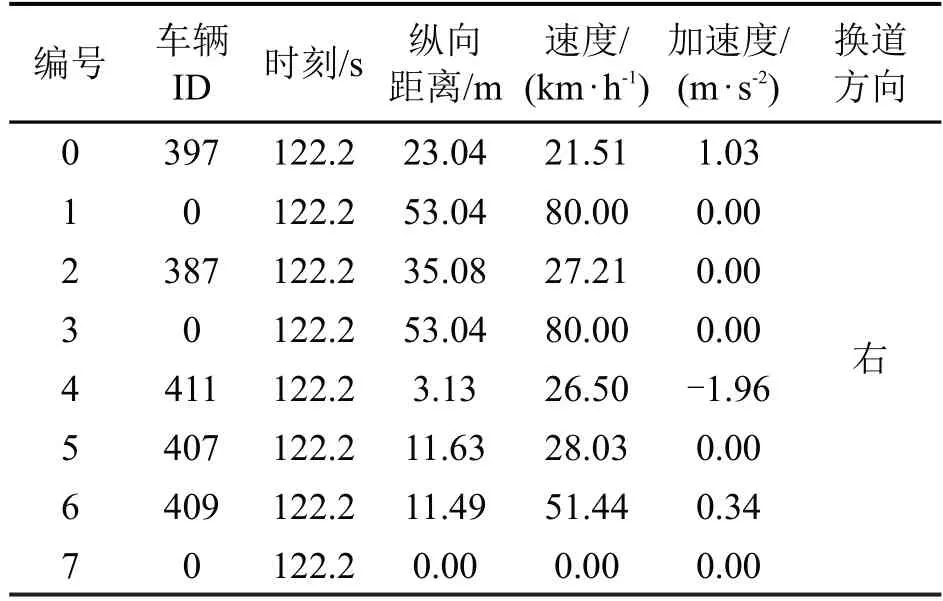
表3 编号397换道决策时刻的车辆组数据Table 3 No.397 vehicle group data at moment of decision to change lanes

(3)驾驶风格聚类

根据车辆在路段上的驾驶表现确定驾驶风格，以纵向速度平均值、纵向加速度标准差、换道频数、速度变异系数[15]及纵向加速度均值绝对值为特征指标，对数据进行Z-score标准化后，选用误差平方和(Sum of Square due to Error,SSE)和CH 系数(CalinskiHarabasz,CH)对k值选取进行评价，评价结果如图8 所示。当簇为k=3 时，SSE 折线出现“肘点”，且此时CH达到最高值，即最佳k值为3，证明了将样本划分为“保守型”“常规型”“冒险型”这3种驾驶风格的合理性。针对主车以及涉及到主车换道环境中的各车辆驾驶风格，进行k-means 聚类分析，得到包含所有换道车辆的驾驶风格样本库分布如表4所示。为可视化驾驶风格聚类结果，通过主成分分析法(Principal Component Analysis,PCA)将5 维特征变量降至3 维，筛选出相关车辆数据绘制聚类可视化图，如图9所示，其中，X,Y,Z轴表示降维后的3个维度，可视化结果显示，3种驾驶风格在空间中区分较清晰，聚类效果较好。

表4 样本库驾驶风格分布Table 4 Sample pool driving style distribution

图8 SSE及CH指标簇评价Fig.8 SSE and CH cluster indicator

图9 相关车辆驾驶风格聚类的可视化图Fig.9 Visualization of driving style clusters

图10(a)～图10(d)分别为纵向速度平均值、加速度标准差、加速度平均值和速度变异系数指标按聚类标签划分的箱型图。从图10(a)可以看出，冒险型风格倾向于高速行驶，且速度较为集中，常规型风格纵向速度的中位数和上下四分位线低于保守型数据，但是，常规型风格的纵向速度相比于其他两类数据分散；从图10(b)可以看出，保守型和常规型风格纵向加速度标准差的中位数和上下四分位数相差不大，与图10(a)有相似的分布趋势，其中，冒险型风格纵向加速度标准差中位数和上下四分位数与其他两类有明显差异，说明冒险型风格具有大幅度加减速操作；从图10(c)和图10(d)可以看出，纵向加速度均值绝对值和速度变异系数的中位线和上下四分位线存在冒险型大于常规型大于保守型的显著关系，除上述特征指标，换道频数对驾驶风格聚类结果的影响较低。综上所述，冒险型标签表征高速行驶和剧烈加减速特征；保守型标签表征较小幅度加减速和速度集中特征；常规型标签相关特征指标分布位于两者之间，且具有速度分散特征。

图10 不同驾驶风格特征指标箱型图Fig.10 Characteristic indicators box plots of different driving styles

(4)横向数据处理

换道横向速度数据由数据集中的字段“Langitude distance”获得，该字段表示车辆中心与当前车道中心曲线之间的距离，正常行驶情境下，当该值发生跃变时，表示车辆中心已经越过车道线，发生变道；当该值跨越0线时，表示车辆越过当前车道中心，如图11(a)和图12(a)所示。将Langitude distance 按车道连续性进行处理得到如图11(b)和图12(b)所示的时空轨迹图，可以直观地展示车辆进行横向位移的过程。

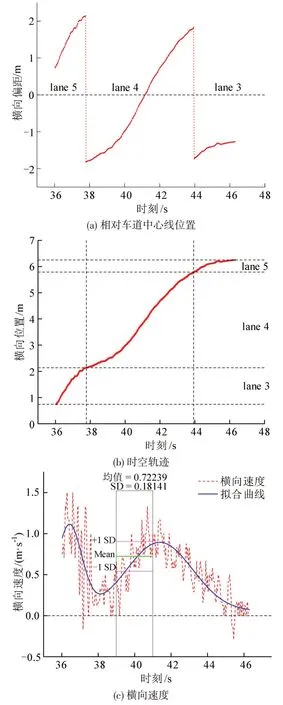
图11 141号车辆时空属性Fig.11 Temporal and spatial properties of vehicle 141

图12 336号车辆时空属性Fig.12 Temporal and spatial properties of vehicle 336

对时空轨迹图进行多项式拟合并求导，获得车辆换道开始过程各采样时刻的横向瞬时速度，经过降噪处理后，获得较平滑的横向速度-时间图，选取方向盘回转时刻前2 s 计算平均横向速度。如图11(c)所示，141号车辆换道发生阶段的横向速度估计为0.72239 m·s-1，表示向左换道；如图12(c)所示，336 号车辆换道发生阶段的横向速度分别估计为0.73581 m·s-1，0.91522 m·s-1，表示该车辆发生两次向左换道。

4.2 参数标定与初步验证

参数标定通常是以模型结果与真实数据之差最小为目标函数的非线性最优化问题，通过不断修正模型参数值使模型结果尽可能接近实际值，即寻找到使两者差距最小的参数。现有研究常采用遗传算法进行参数标定，但遗传算法的搜索速度比较慢，且局部搜索能力比较差，较易产生早熟收敛的问题，而蚁群算法中每只蚂蚁搜索过程彼此独立，仅通过信息激素进行通信，可以看作是一个分布式的多智能体系统，在问题空间的多点同时开始进行独立的解搜索，不仅增加了算法的可靠性，也使算法具有较强的全局搜索能力，故本文采用蚁群算法(Ant Clony Optimization,ACO)标定所建立的换道决策模型参数。具体流程如图13所示。

图13 蚁群算法流程Fig.13 Ant colony algorithm process

初步按72%∶28%的比例将数据集划分为训练集与验证集，通过蚁群算法进行标定，验证模型的可行性，本文选取表示数据序列与真实值之间关系的均方根误差(Root Mean Square Error,RMSE)值最小为目标函数，即

式中：x为需要进行误差分析的指标，在本模型中，为向目标车道开始换道阶段的横向平均速度；为决策模型对第i个样本的横向速度预测值；I为样本量为第i个样本的横向速度真实值。获得初步标定结果如表5所示。

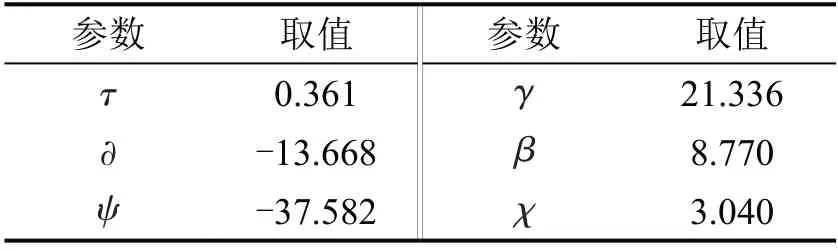
表5 参数初步标定结果Table 5 Preliminary calibration results of parameters

由于横向速度的正负分别表示预测结果为向左换道和向右换道，故采取符号函数判断预测是否正确，即

式中：xi为预测值与真实值的乘积；sgn(xi)为输入为xi的符号函数。当预测值与真实值同号，sgn(xi)=1 时，模型结果为正确；预测值与真实值异号，sgn(xi)=-1时，模型结果为错误。

模型正确率r为

式中：NT为验证集中识别正确的样本量；NF为验证集中识别错误的样本量。

将参数标定结果代入模型中，对剩余数据集进行验证，得到换道预测结果如图14(a)所示，得到换道预测正确率为91.42%，证明了该模型的有效性。

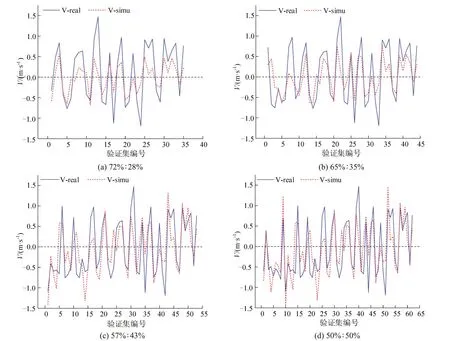
图14 不同训练集与验证集比例下最优模型实际结果与模型结果对比Fig.14 Comparison of actual results and model results with different training set-validation set ratios

4.3 模型泛化能力验证

为避免模型对数据的过拟合，在使用72%∶28%的训练集与验证集比例验证模型有效性的基础上，通过设置不同的训练集与验证集比例，采用随机排列交叉验证(Random Permutations Cross-Validation,RPCV)方法进行多次参数标定及验证，以随机划分集的平均正确率作为评估模型的预测效果和泛化性能的指标。

不同训练集与验证集比例下，获得的最优模型对应的预测结果如图14 所示，实线中的编号点表示真实值V-real，虚线中的编号点表示预测值V-simu，真实值和预测值随样本的变化趋势基本一致，证明了不同训练与验证比下，标定后的模型对于结果的敏感性。

为形象表示模型预测效果，绘制预测效果散点图，如图15所示。预测获得的横向速度较小，大多在[-0.8,0.8]m·s-1内，未出现离群点，说明该模型的计算结果较稳定，且可使车辆实现决策下的平稳换道。识别错误的样本中，其横向速度的预测值集中在0 值附近，经过轨迹验证，该类车辆存在换道横向摆动的现象较多，反映拟人换道决策时驾驶人的犹豫心理，使横向速度识别产生误差，对模型结果产生一定干扰。

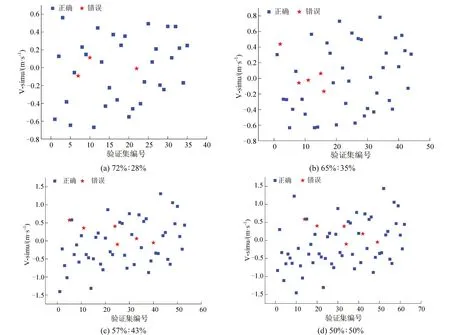
图15 模型预测效果散点图Fig.15 Scatterplot of model prediction effects

经统计，模型预测正确率如表6所示。当训练集与验证集比例为72%∶28%时，最优模型总体正确率为91.42%，其中，向左换道预测正确率达到89.47%，向右换道预测正确率达到93.75%，随机划分训练集与验证集比例下所获得的不同模型的平均正确率为90.34%；当训练集与验证集比例为65%∶25%时，最优模型总体正确率为88.64%，其中，向左换道预测正确率达到86.36%，向右换道预测正确率达到90.91%，随机划分训练集与验证集比例下所获得的不同模型的平均正确率为86.67%；当训练集与验证集比例为57%∶43%时，最优模型总体正确率为88.68%，其中，向左换道预测正确率达到91.30%，向右换道预测正确率达到86.67%，随机划分训练集与验证集比例下所获得的不同模型的平均正确率为88.82%；当训练集与验证集比例为50%∶50%时，最优模型总体正确率为90.32%，其中，向左换道预测正确率达到92.00%，向右换道预测正确率达到89.18%，随机划分训练集与验证集比例下所获得的不同模型的平均正确率为89.21%。结果表明，本文所建立的模型精度较高，泛化能力较好，且具有一定的鲁棒性。

表6 最优模型正确率和随机划分集平均正确率Table 6 Correctness of optimal model and average correctness of randomly divided set

4.4 模型对比

为进一步评价本文所建换道决策模型的合理性，分别选取支持向量机(Support Vector Machines,SVM)、随机森林(Random Forest,RF)、朴素贝叶斯(Naïve Bayse,NB)、K-近邻算法(K-Nearest Neighbor,KNN)、逻辑回归(Logistic Regression,LR)与本文模型进行性能对比，使用相同的数据集评估上述模型性能。为保证各模型输入输出参数的同质性，将本文模型中涉及到的所有基础参数作为对比模型的输入参数，以正确率为输出参数，为避免模型过拟合，采用随机排列交叉验证方法，取平均正确率作为模型预测效果对比指标。

由于输入参数维度较高，为降低噪声信息对模型性能的干扰，通过主成分分析法PCA 指定解释方差百分比为95%，85%，75%分别选取主成分，搜索其他分类器在决策中的最优性能。模型性能对比结果如表7 所示，从预测结果可以看出，本文提出模型的正确率与SVM、KNN、LR、RF 和NB 相比分别高2.5%、4.1%、4.9%、8.1%和9.8%，说明本文所提出的模型性能更优。

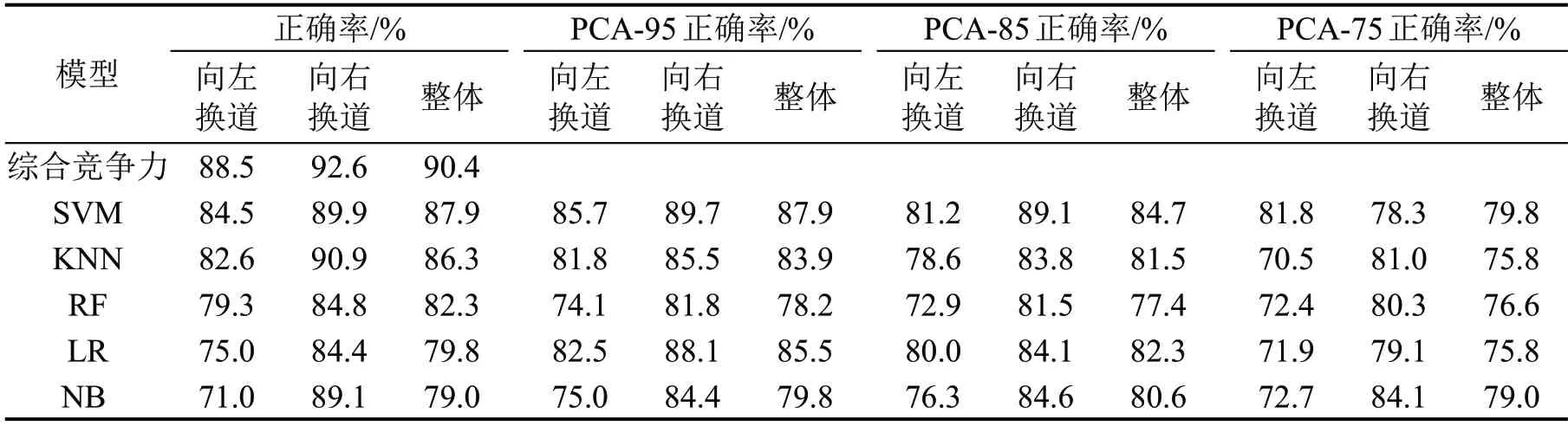
表7 模型性能对比结果Table 7 Model performance comparison results

5 结论

本文构建以引力理论为框架，以综合竞争力为媒介，以车辆横向速度为求解目标的自动驾驶拟人换道决策模型。主要创新点如下：考虑换道车辆驾驶风格的影响并根据邻近前车间距和速度差建立换道意愿函数，引入虚拟单元解决前方无车情境下换道意愿无法量化的问题；提出一种基于悲观主义原则的换道竞争行为分析方法，假设周围车辆均与主车产生竞争行为，基于车头间距比和驾驶风格差提出车辆个体间的潜在竞争强度概念，用低复杂度函数衡量主车各决策下的换道优势，有效客观地刻画车辆之间的交互行为及其对换道决策产生的影响；以换道意愿为等效引力常量和综合竞争强度为等效质量，以速度“伪距”和加速度“伪距”为等效距离，应用引力理论的正反比关系，构建用于决策选择的竞争力表达式。

本文得出的主要结论如下：

(1)当训练集与验证集比例为72%∶28%时，最优模型总体正确率为91.42%，说明本文提出的换道决策模型具有可行性。采用RPCV 方法进行模型泛化能力评估，随机划分集平均正确率稳定分布在87.67%～90.34%内，说明本文模型在不同训练集与验证集比例下具有较强的鲁棒性和泛化能力。

(2)与SVM、KNN、LR、RF 和NB 模型相比，本文模型在正确率上分别高出2.5%，4.1%，4.9%，8.1%和9.8%，说明本文模型较传统模型在决策性能上具有一定的优越性。

(3)本文构建的换道决策模型结构清晰且输入输出关系明确，以道路上车辆运行的真实轨迹数据为依据标定模型参数，相比于数据驱动的换道决策模型更具有解释性，为自动驾驶环境下的拟人化换道决策过程提供建模思路，也为自动驾驶车辆换道决策机制和换道状态评估等研究提供支持和依据。