集装箱海铁联运补贴优化研究

吴云强，解乔雅，张戎*,b

(同济大学，a.城市交通研究院；b.道路与交通工程教育部重点实验室，上海 201804)

0 引言

海铁联运具有运量大、可靠性高、成本低及污染少等突出优势，随着交通强国建设和运输结构优化调整的深入，海铁联运已成为“十四五”现代综合交通运输体系发展规划中重点推进的港口集疏运模式。据统计，2022 年，全国沿海港口集装箱海铁联运量834万TEU，同比增长14.3%，占港口集装箱吞吐量比重上升到3.2%。其中，海港所在城市向承运人和托运人提供的补贴对丰富海铁联运货源品类和提高运量起到了关键作用。然而，由于缺乏决策支持工具，目前，补贴政策仍存在补贴水平不科学和实施效果不可预见等问题。此外，各海港所在城市均基于自身利益最大化制定补贴政策，存在重复补贴和过度补贴等非理性竞争行为，偏离了市场运行的客观规律。若各海港所在城市之间加强合作，进行协同补贴，将在控制补贴总量的基础上进一步提高海铁联运市场份额，并避免补贴资金因无效竞争而浪费。因此，如何从全局最优角度出发，制定服务于多个海港的协同补贴方案对海铁联运的高质量和可持续发展至关重要。

关于货运补贴问题，现有研究主要分为两类：补贴效果评估和补贴优化。针对补贴效果评估，最常见的评价指标是两种运输方式之间转移的货运量[1]。同时，补贴的主要目的是优化运输结构，降低碳排放。因此，CO2排放量也是重要的评价指标[2]。此外，补贴优化相关文献较少，这类研究主要基于多式联运网络构建数学规划模型，优化补贴机制。例如，宋达宽[3]分析海铁联运运价和补贴对货主运输链选择的影响，以收益最大为目标，构建定价方案与补贴水平决策模型。YANG等[4]对比分析不补贴、外部成本内部化、不协同补贴及协同补贴这4 种政策对中欧班列的影响。FENG等[5]基于当地政府、平台公司及托运人之间的作用机制，提出中欧班列最佳补贴金额。谢雨蓉等[6]对比分析政府根据发送量目标和社会福利最大对中欧班列的最优补贴决策。YIN等[7]考虑运营成本、外部成本及中转成本等因素的影响，构建双层规划模型，确定中欧班列补贴方案。HU等[8]以内河水运市场份额最大和补贴金额最少为优化目标，确定3种不同规则下的补贴方案。徐菱等[9]构建由政府、运营平台及货主组成的三级博弈模型，分析统一定价补贴机制和差异化定价补贴机制下中欧班列各主体最优决策。

综上，现有学者主要关注中欧班列补贴优化，罕有涉及海铁联运。同时，在运输方式选择中，多数研究仅考虑了两种运输方式。此外，既有研究通常假设一个代表所有托运人的决策者基于费用最小化原则选择运输方式，未考虑运输资源有限条件下托运人之间的竞争问题，即忽略了运输能力的影响。因此，本文以3种运输方式、两个起运港、腹地城市及目的港形成的运输系统为研究对象，利用能力约束型巢式Logit 模型描述托运人选择行为，基于补贴政策下政府与托运人之间的作用机制，从全局最优角度出发，制定海铁联运协同补贴方案，并对比分析不补贴、不协同补贴及协同补贴这3种场景下各种运输方式的市场份额。

1 集装箱出口运输流程、费用及时间分析

1.1 集装箱出口运输流程

由于我国外贸具有出口大于进口，进口和出口流程类似，方向相反，且海铁联运出口重箱数量远超过进口等特点，故本文以集装箱货物出口为例，研究海铁联运补贴优化问题。集装箱货物出口运输流程如图1所示，包括：公海联运、海铁联运及水水联运这3种运输方式。其中，空箱是尚未装载货物的集装箱，重箱是已装载货物的集装箱，港前站是紧邻起运港的铁路车站。在3种运输方式中，起运港与目的港之间均通过海运完成运输，腹地城市与起运港之间分别采用公路、铁路及内河水运完成空箱调运和重箱集港运输。海铁联运只会经过1 个内陆铁路车站和1 个港前站，水水联运只会经过1 个内河港口。同时，当托运人选择水水联运时，可直接在内河港口提取空箱，如果选择另外两种方式，则需要从起运港提取空箱。此外，根据港前站的位置可以将海铁联运分为两种形式：一是，港前站设置在港区外面，即港前站与起运港之间具有一定距离，列车到达港前站后，需通过外集卡才能将重箱运到港区堆场，目前，采用这种形式的港口有青岛港和上海港等；二是，港前站设置在港区里面，即港前站与起运港之间的短驳距离为零，列车到达港前站后，可直接将重箱卸到港区堆场，目前，采用这种形式的港口有大连港、天津港、连云港港及宁波舟山港等。

图1 出口运输流程Fig.1 Export transportation process

1.2 集装箱运输费用与时间

由于相邻起运港到达同一目的港的海运费和运输时间基本相同，本文不考虑国际海运段运输，只关注腹地城市和起运港之间的内陆段运输，以及起运港的费用与时间。此外，空箱已在托运人装箱之前调运至工厂，故忽略空箱调运时间的影响。因此，内陆段运输只考虑空箱运输费用、重箱运输费用及重箱运输时间。

为便于分析，定义相关符号表示图1中的运输方式与运输节点。令I表示腹地城市集合，i∈I；V表示内河港口集合，v∈V；J表示内陆铁路车站集合，j∈J；H表示港前站集合，h∈H；S表示起运港集合，s∈S；K表示运输方式集合，k∈K，k={1,2,3} 分别表示公海联运、海铁联运及水水联运；βiskm表示运输方式与中转节点m(m∈V⋃J⋃H)的关系，如果等于1，位于城市i的托运人选择起运港s与运输方式k出口货物时，经过节点m，否则为0。

(1)起运港相关费用与时间

起运港服务费用Es是影响托运人选择起运港s的重要因素之一。Es指重箱在起运港作业过程中所产生的费用，包括：货物港务费、港口设施保安费及码头操作费。

在港等待时间Ts指出口重箱从到达起运港s到其所装载船舶开始离泊的时间，主要考虑船舶在港时间与货物通关时间，其将带来保险、折旧、现金流限制及货物时间敏感性等方面的成本。Ts可通过货物时间价值以货币形式表现出来，后续运输时间采用同种方式货币化。

(2)内陆段运输相关费用与时间

①公海联运

公海联运(k=1)对应的内陆段运输方式为公路运输。公路全程运输费用指托运人向承运人所支付的完成腹地城市i与起运港s之间空箱和重箱运输的费用，可表示为城市i和起运港s之间的公路运距Lis与公路运输单位费率Broad的乘积。因此，位于城市i的托运人选择起运港s与公海联运出口货物时，内陆段运输费用Cisk为

公路全程运输时间指将重箱从腹地城市i运到起运港s所需的时间，可表示为运距与集卡行驶速度ψroad的比值。因此，位于城市i的托运人选择起运港s与公海联运出口货物时，内陆段运输时间Tisk为

②海铁联运

海铁联运(k=2)对应的内陆段运输方式为铁路运输。铁路全程运输费用包括空箱和重箱运输产生的公路短驳费用、内陆铁路车站j和港前站h装卸作业费用、内陆铁路车站与港前站之间的铁路运费以及政府提供的补贴。由于海铁联运只会经过1 个内陆铁路车站和1 个港前站，因此，且βis2j=1，βis2h=1分别表示位于城市i的托运人选择起运港s与海铁联运出口货物时经过的内陆铁路车站为j和港前站为h。此外，政府补贴在实际中提供给海铁联运承运人，本文为简化分析，假设补贴直接提供给托运人，且金额不变。位于城市i的托运人选择起运港s与海铁联运出口货物时，内陆段运输费用Cisk为

当港前站设置在港区外面时

当港前站设置在港区里面时

式中：Fij为公路运输企业将空箱从内陆铁路车站j运到城市i，待客户装箱后，将重箱运回车站j收取的短驳费用；Fhs为公路运输企业将空箱从起运港s运到港前站h或将重箱从港前站h运到起运港s收取的短驳费用；为铁路运输重箱装卸作业费；为铁路运输空箱装卸作业费；Ljh为内陆铁路车站j与港前站h之间的铁路运距；为铁路运输重箱发到基价；为铁路运输重箱运行基价；为重箱铁路建设基金费率；为铁路运输空箱发到基价；为铁路运输空箱运行基价；为空箱铁路建设基金费率；Xjs为政府对由内陆铁路车站j开往起运港s的海铁联运班列所提供的单个重箱补贴金额。

铁路全程运输时间主要考虑公路短驳运输时间、班列行驶时间及在内陆铁路车站等待时间Tj。其中，短驳时间指腹地城市i与内陆铁路车站j之间和港前站h与起运港s之间的重箱运输时间，Tj指重箱从到达内陆铁路车站直到其装上班列出发所需时间。令Lij表示城市i与内陆铁路车站j之间的公路运距，Lhs表示港前站h与起运港s之间的公路运距，ψrail表示火车行驶速度。位于城市i的托运人选择起运港s与海铁联运出口货物时，内陆段运输时间Tisk为

③水水联运

水水联运(k=3)对应的内陆段运输方式为内河水运。由于水水联运只会经过1个内河港口，因此，=1，且βis3v=1 表示位于城市i的托运人选择起运港s与水水联运出口货物时经过的内河港口为v。内河水运大多采用以箱为单位的计费方式，实行包箱费率。包箱费率Bwater是船公司根据自身情况以不同类型集装箱为单位确定不同航线的包干费，通常包含水运运费及码头装卸作业费。内河水运全程运输费用包括包箱费和腹地城市i与内河港口v之间的短驳费用。令Lvs表示内河港口v与起运港s之间的水运运距，Fiv表示公路运输企业将空箱从内河港口v运到城市i，待客户装箱后，将重箱运回v收取的短驳费用。位于城市i的托运人选择起运港s与水水联运出口货物时，内陆段运输费用Cisk为

类似于铁路运输，内河水运全程运输时间包括：公路短驳运输时间、船舶行驶时间及在内河港口等待时间Tv。令Liv表示城市i与内河港口v之间的公路运距，ψwater表示内河船舶行驶速度。位于城市i的托运人选择起运港s与水水联运出口货物时，内陆段运输时间Tisk为

2 构建协同补贴双层优化模型

本文假设各起运港所在城市的政府之间通过合作进行协同补贴，即各起运港所在城市的交通主管部门之间通过建立合作机制，以整个运输网络中海铁联运运量最大为目标，确定最佳的海铁联运协同补贴方案。政府根据集装箱货物运输过程中海铁联运运量的大小，向托运人提供补贴。政府的补贴政策会影响托运人对起运港与运输方式的选择行为，其选择行为改变后，海铁联运运量也会发生改变，反过来，影响政府的协同补贴方案。因此，本文构建双层规划模型描述集装箱运输系统中政府与托运人的相互作用，实现协同补贴方案的优化。其中，上层模型，以海铁联运运量最大为目标，以海铁联运班列单个重箱补贴金额为决策变量；下层模型，描述补贴方案下托运人对起运港和运输方式的选择行为，通过构建能力约束型巢式Logit模型，将集装箱货物流量分配到整个运输网络中。

2.1 下层模型——能力约束型巢式Logit模型

上层模型给定协同补贴方案，决定内陆段运输费用，影响托运人的选择行为。为将出口货物运到目的港，托运人需要选择起运港与运输方式。本文引入传统巢式Logit 模型结构描述托运人选择行为。即托运人首先选择起运港，再从访问该起运港的运输方式集中选择最有利的方式。

根据巢式Logit模型理论，位于城市i的托运人选择起运港s的概率为

位于城市i的托运人在选择起运港s的条件下选择运输方式k的概率为

式中：Uisk为位于城市i的托运人在选择起运港s的条件下，选择运输方式k的确定效用，可表示为内陆段广义运输费用(运输费用与运输时间成本之和)的相反数；Uis为位于城市i的托运人选择起运港s的确定效用，可表示为起运港广义运输费用(起运港服务费用与在港等待时间成本之和)的相反数；λ1、λ2为模型参数，可用以统一效用之间的对比测度关系；为上层起运港s包含的运输方式对位于城市i的托运人选择起运港s的影响变量。令Y表示集装箱货物平均时间价值，各变量计算式为

根据选择概率与城市i集装箱货物出口数量Oi，城市i的托运人选择起运港s出口的货物数量μis和位于城市i的托运人选择起运港s与运输方式k出口的货物数量μisk的计算式为

本文考虑运输能力约束，因此，需要改进传统巢式Logit 模型，从而包含相关约束。依据熵最大化原理，本文构建能力约束型巢式Logit 模型(Capability Constrained Nested Logit Model,CCNLM)，将能力约束融入托运人选择行为之中，且此模型的结果满足传统巢式Logit模型的选择概率公式[10]。CCNLM模型为

式中：ϕms为中转节点m与起运港s之间的最大运输能力。式(20)表示与托运人对起运港与运输方式选择行为的熵值最大有关的函数；式(21)和式(22)为流量守恒约束；式(23)为内河港口与起运港之间的水运运输能力约束，内陆铁路车站与起运港之间的海铁联运班列运输能力约束。

2.2 上层模型——协同补贴方案决策模型

上层模型从假设制定海铁联运补贴政策的政府部门的角度出发，以海铁联运运量最多为目标，确定政府对由内陆铁路车站j开往起运港s的海铁联运班列所提供的单个重箱补贴金额Xjs。令Djs为海铁联运班列单个重箱最高补贴金额，Q为补贴总额上限。上层模型构建为

式(24)为目标函数，表示海铁联运运量最多。由于海铁联运只会经过1 个内陆铁路车站，因此，经所有内陆铁路车站中转的集装箱货运量即为海铁联运运量；式(25)表示海铁联运班列单个重箱补贴金额上限约束；式(26)表示补贴总额不能超过预算；式(27)表示变量取值范围。

3 算法设计

双层规划问题是一个NP-hard 问题，即使寻找双层线性规划问题的局部最优解仍是NP-hard 问题。常见的解决方法是通过Karush-Kuhn-Tucker(KKT)条件将双层模型转换为单层模型。因此，本文的算法流程为：首先，利用KKT条件将协同补贴双层优化模型转化为等价的单层模型；其次，由于模型存在互补条件，利用松弛迭代算法求解模型。

3.1 模型转化

下层CCNLM 是一个凸优化模型，且满足Slater 约束规范性条件，因此，满足KKT 条件的解一定是CCNLM 最优解。设置ϖi、σis、τms分别为式(21)～式(23)的拉格朗日乘子，构造广义拉格朗日函数，即

CCNLM 的KKT 条件可表示为式(21)～式(23)和式(29)～式(32)。因此，CCNLM利用其KKT条件代替，将协同补贴双层优化模型转化为单层规划模型。其中，目标函数为式(24)，约束条件为式(21)～式(23)、式(25)～式(27)及式(29)～式(32)。

3.2 松弛迭代算法

由于存在互补条件，该单层非线性规划模型是非凸的，且直接求解该模型是困难的。本文采用松弛算法迭代求解该模型，即对每个互补条件引入1 个辅助参数θ定义松弛的互补条件，在每次迭代时，互补约束条件式(31)由式(33)代替。该松弛迭代算法具体步骤如下。

Step 1 参数设置

迭代次数r，辅助参数θr，更新因子λ，上限ξ。

Step 2 模型求解

式(33)中的辅助参数θ的取值为θr，应用Matlab 中Fmincon 函数求解松弛单层非线性规划模型。

Step 3 终止条件

若θr≤ξ，停止迭代，输出最优解；否则，θr+1=λ⋅θr，转到Step 2。

4 算例分析

4.1 案例描述

本文将模型与算法应用于上海港、宁波舟山港及其腹地形成的运输网络，如图2 所示，并以2021年数据进行分析。随着长三角区域一体化的推进，2018年，“三省一市”共同成立长三角区域合作办公室。该机构的目的在于协调各省份在多领域的合作意向，发挥统筹作用，涵盖交通、产业、环保、能源及金融等领域。因此，本文假设上海市交通委员会与宁波市交通运输局依托于长三角区域合作办公室，协同制定海铁联运补贴方案。在浙江省、江苏省、安徽省、江西省及湖北省分别选择外贸出口额排名前8 的城市与上海市作为研究的腹地城市。各城市货运需求量根据出口额、海运出口比例及单箱货物价值估算。内河港口包括太仓、南京、芜湖、九江及武汉这5 个沿长江较大集装箱港口以及南昌和合肥两个与长江相通的港口，并通过长江和东海与上海港和宁波舟山港相连。每个内河港口与上海港和宁波舟山港之间的水运运输能力来自WU等[11]的研究。选取16个内陆铁路车站，上海港与宁波舟山港的港前站分别为芦潮港站和北仑港站，芦潮港站设置在港区外面，距离洋山港区42 km，北仑港站设置在港区里面。

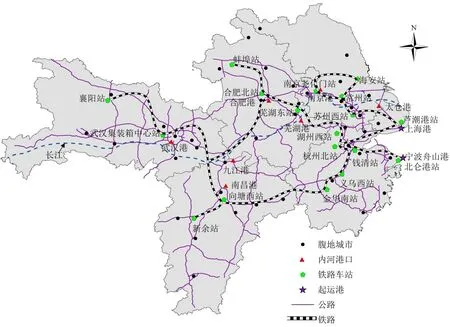
图2 运输网络Fig.2 Transportation network

根据《铁路货物运价规则》，铁路运输重箱发到基价为440 元·TEU-1(Twenty-feet Equivalent Unit,TEU)，重箱运行基价为3.185元·(TEU·km)-1，重箱、空箱铁路建设基金费率分别为0.528元·(TEU·km)-1，0.264 元·(TEU·km)-1。当自备集装箱空重联运时，空箱运价率按对应箱型重箱基准运价率的10%计费，建设基金同比例核收。根据《铁路货物装卸作业计费办法》，内陆铁路车站与芦潮港站重箱装卸作业费为195 元·TEU-1，空箱为45 元·TEU-1。根据实地调研，北仑港站重箱装卸作业费为125元·TEU-1，空箱为113元·TEU-1。中国铁路上海局集团对管内重箱实行内陆铁路车站与港前站之间的铁路运费下浮50%(管外30%)，内陆铁路车站与芦潮港站的装卸作业费下浮50%(管外发站装卸作业费下浮50%，芦潮港站下浮30%)的优惠。同时，上海港免收空箱和重箱在芦潮港站与港区之间的短驳费用。此外，海铁联运单个重箱补贴不能超过内陆铁路车站与港前站之间的铁路运费。模型参数λ1为0.0046，λ2为0.005。其他数据来自港口官网、中国铁路95306、相关研究[11-13]及实地调研，如表1所示。

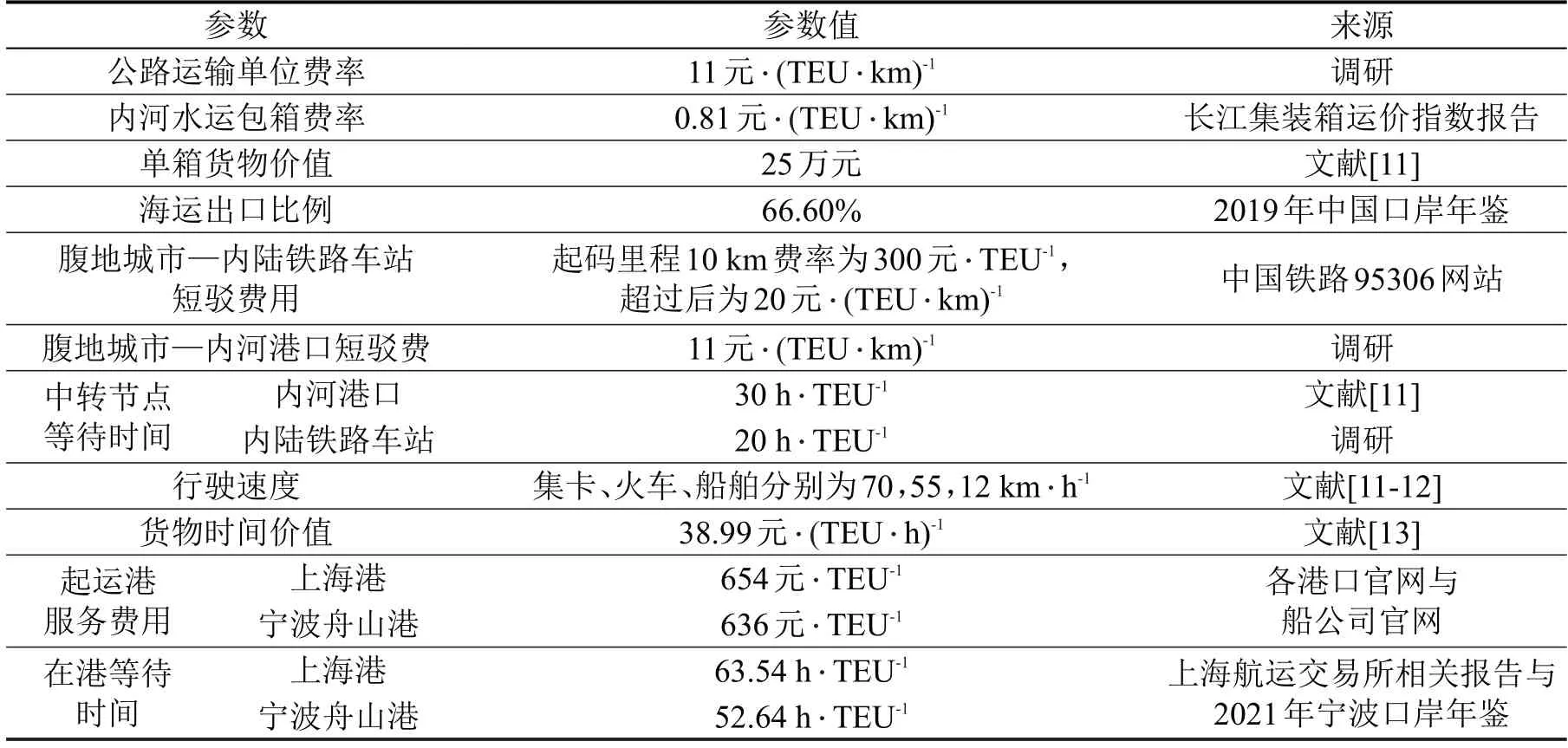
表1 相关参数取值Table 1 Related parameter values

4.2 模型验证

为验证CCNLM 模型与相关参数取值是否适合，本文根据2021 年海铁联运班列开行方案和补贴政策，将两个起运港扣除国际中转和水水中转重复计算箱量的实际集疏运结构与利用本文模型计算得到的仿真数据进行比较，如表2 和表3 所示。由于本文所研究区域为两个起运港的主要腹地，因此，两种数据之间具有可比性。结果表明，实际值与仿真值之间的决定系数R2为0.99，且各种运输方式以及起运港的市场份额与实际数据基本符合，即模型具有良好拟合效果。因此，本文所提出的CCNLM 模型可以较好地表示托运人对起运港与运输方式的选择行为，且相关参数取值合理。

表2 班列数量与补贴方案Table 2 Number of trains and subsidy scheme

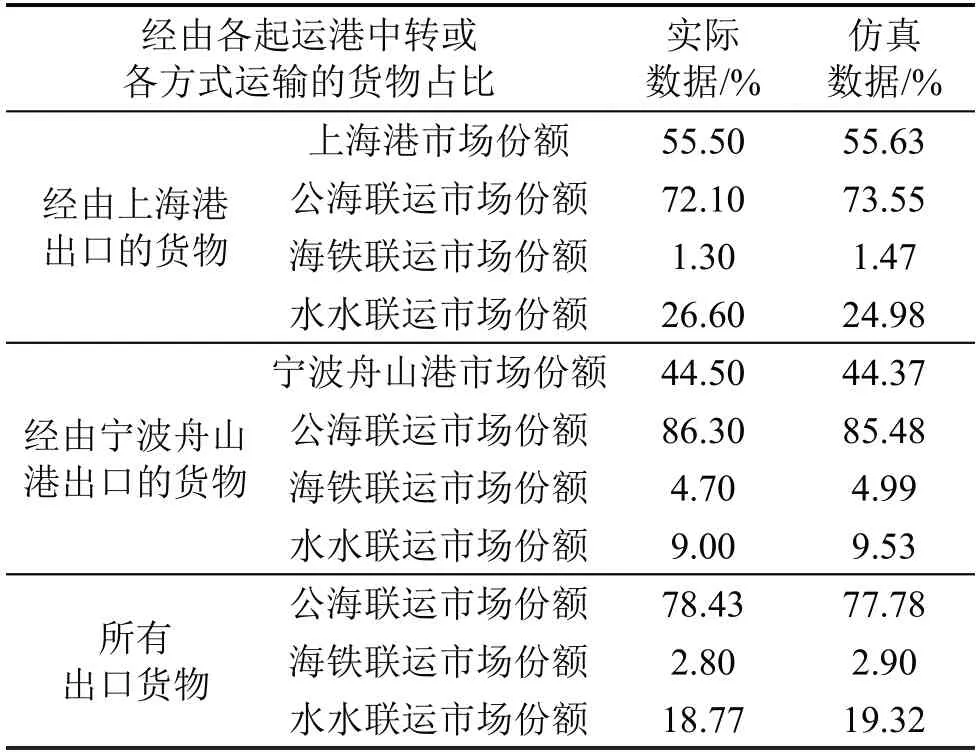
表3 结果比较Table 3 Comparison of results

4.3 3种场景对比分析

为更好地进行比较分析，针对每周数量小于7的海铁联运班列，本文假设其为7，即每天一班。协同补贴时的补贴总额上限为按照表2 补贴方案(不协同补贴)所消耗的金额。不补贴(场景1)、不协同补贴(场景2)及协同补贴(场景3)这3种场景下的计算结果如表4所示。

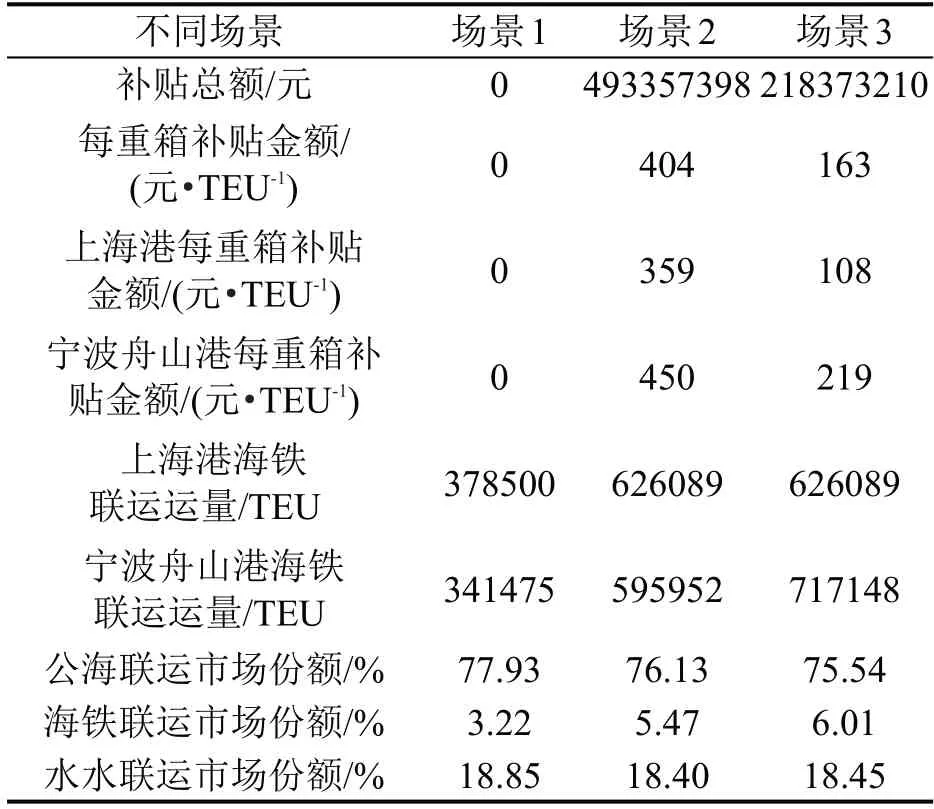
表4 不同场景的计算结果Table 4 Calculation results for different scenarios

由表4 可知，相比于场景2，场景3 使海铁联运运量达到海铁联运班列运输能力上限(市场份额占比6.01%)，补贴总额下降了55.74%，且每箱补贴金额下降了59.73%。具体来看，上海港海铁联运运量没有变化，而每箱补贴金额降低了69.92%；宁波舟山港海铁联运运量上升了16.9%，且每箱补贴金额降低了51.33%。因此，本文所提出的同时考虑多个起运港的协同补贴方案远优于现在每个起运港从自身利益出发单独制定的不协同补贴方案，可以最小的补贴费用最大化海铁联运运量。其次，相比于场景1，场景2 与场景3 提高了海铁联运竞争力，使市场份额分别增加了2.25%与2.79%。同时，水水联运与公海联运市场份额均呈现下降趋势。其中，场景2 与场景3 使水水联运份额分别仅下降了0.45%与0.40%，而公海联运份额分别下降了1.80%与2.39%。因此，补贴引起的海铁联运运量的增长大部分来自于公海联运转移的货运量，少部分来自于水水联运转移。安徽省、湖北省及江西省出口的集装箱货物中海铁联运运量增长主要来自于水水联运转移的货运量，而江苏省和浙江省海铁联运运量增长主要来自于公海联运转移量。此外，尽管海铁联运补贴对水水联运市场份额影响较小，由于它们都是低碳运输方式，两者之间的运输模式转移将会导致运输资源和补贴资金的浪费。这一结果也证明，相比于既有研究只考虑公海联运与海铁联运，本文同时考虑3种运输方式更具有理论与现实意义。

4.4 协同补贴方案分析

根据本文模型与算法计算得到的协同补贴方案如图3所示。平均而言，每个海铁联运班列补贴金额为141 元⋅TEU-1，利用率为100%。其中，利用率为海铁联运运量与班列运输能力的比值。结合图2可知，尽管海铁联运的优势随着运距(内陆铁路车站与起运港之间的距离)的增加而变大，补贴金额并不完全是随着运距的增大而减小。例如，钱清站—上海港补贴金额为106元⋅TEU-1，而武汉铁路集装箱中心站—宁波舟山港补贴金额为169 元⋅TEU-1。由此可见，运距只是影响补贴金额的一个重要因素，货运需求量、其他运输方式及短驳距离等因素均会对其产生影响。因此，本文所采用的基于海铁联运班列的补贴方法优于以往文献中基于距离的补贴方法与固定金额方法，即根据内陆铁路车站开往起运港的海铁联运班列的具体情况设置补贴金额。

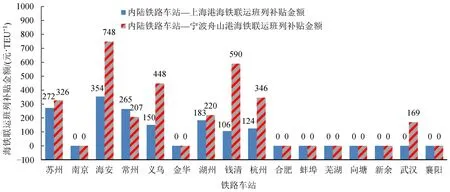
图3 补贴方案Fig.3 Subsidy scheme

此外，依据是否需要提供补贴，可将图3 中的海铁联运班列分为两种：政府不提供补贴和政府提供补贴。影响第一类班列(补贴为0)海铁联运运量的最关键因素是运输能力，政府可以增加班列开行密度，或采用双层集装箱列车吸引更多托运人选择海铁联运。这些班列主要服务距离起运港较远的安徽省、江西省及湖北省。由于这些区域的出口货运需求量较少，其对未来海铁联运运量增长的作用有限。同时，水水联运是上述区域费用最低的运输方式，且水水联运比海铁联运更为环保，因此，这些区域不是理想的海铁联运运量来源地。第二类班列(补贴大于0)是政府提供补贴的班列，这些班列服务于距离起运港较近的江苏省和浙江省，上述地区是上海港和宁波舟山港主要腹地，具有大量货运需求，且现在所采用的主要运输方式为公海联运，因此，这些区域的班列需要重点关注，是未来海铁联运运量增长的主要来源，且运量增长主要来自公海联运转移量，有助于优化港口集疏运结构与加快交通领域“双碳”目标的实现。

4.5 时间价值影响分析

为分析货物时间价值对补贴效果的影响，本文将其分别设为0，10，20，30，40，50，60，70，80，90，100 元·(h·TEU)-1，补贴总额上限为1 亿元，计算结果如图4 所示。在3 种方式中，公海联运运输时间最短，海铁联运次之，水水联运最长。因此，随着时间价值的变大，水水联运市场份额大幅降低，公海联运市场份额显著增长，海铁联运市场份额呈现先增加后减少的变化趋势。海铁联运运量增加情况的曲线证明，补贴效果会受到货物时间价值的影响，当时间价值从0 增长到40 时，补贴效果逐渐增强，此时，政府所需提供的单箱补贴金额降低；当时间价值从40 增长到100 时，补贴效果逐渐减弱，此时，政府需要提高单箱补贴金额。表明为充分发挥补贴的作用，政府应该向具有中等时间价值货物的托运人提供海铁联运补贴，主要原因是具有低等时间价值货物的托运人会选择更为环保的水水联运，补贴高等时间价值货物的托运人难以奏效。

图4 时间价值对补贴的影响Fig.4 Impact of time value on subsidies

5 结论

补贴是政府为改善港口集疏运系统所采取的一种常见手段。本文基于政府与托运人之间的作用机理，综合考虑运输能力约束、托运人选择行为及起运港竞争，通过构建双层规划模型探究海铁联运协同补贴问题。主要结论如下：

(1)相比于不协同补贴，协同补贴使海铁联运市场份额增加了9.87%，补贴总额下降了55.74%，且单箱补贴金额降低了59.73%。说明从全局最优角度出发，协同制定服务于多个起运港的海铁联运补贴方案优于每个起运港基于自身情况单独制定的方案。

(2)补贴政策能够促进海铁联运运量的增长，并导致公海联运和水水联运市场份额的减少。同时，海铁联运增加的运量主要来自公海联运转移的货运量，少量来自于水水联运转移。算例结果表明，相比于不提供补贴，不协同补贴方案和协同补贴方案使水水联运份额分别仅下降了0.45%和0.40%，而公海联运份额分别减少了1.80%和2.39%。

(3)海铁联运班列单箱补贴金额不仅取决于运距，还与货运需求量和其他运输方式费用等因素有关。此外，根据是否需要提供补贴可将海铁联运班列划分为两大类，政府可以分别采取优化补贴方案与改善运输能力提高海铁联运运量。

(4)补贴政策所能增加的海铁联运运量随时间价值的变大呈现先增长后降低的变化趋势，且生产具有较低时间价值货物的托运人更愿意选择水水联运，而较高时间价值货物所对应的托运人更喜欢公海联运。因此，货物时间价值对补贴效果有影响，政府应着重补贴具有中等时间价值货物的托运人，最大化补贴政策的效益。