计及安全性与舒适性的智能车辆换道轨迹规划研究

陈峥，赵文龙，郭凤香*，赵志刚，刘昱，刘永刚

(1.昆明理工大学，交通工程学院，昆明 650500；2.北京航天发射技术研究所，北京 100000；3.中国汽车技术研究中心有限公司，天津 300300；4.重庆大学，机械传动国家重点实验室，重庆 400044)

0 引言

智慧交通系统是当前交通领域乃至交通相关领域的研究热点，作为其中最重要的一环，智能车辆的发展显得尤为关键。智能车辆相比于人工驾驶车辆，不仅可以提高通行效率，还可以降低交通事故率[1]。智能车辆的研究主要集中在环境感知、轨迹规划和跟踪控制等方面[2]，轨迹规划是智能车辆的环境感知模块与跟踪控制模块之间的重要桥梁。

轨迹规划最早出现在智能机器人领域，目的是为了寻找机器人的最优路径，车辆的轨迹规划方法是在机器人轨迹规划方法的基础上加以优化和改进，以达到适应复杂多变的交通环境的目的，而换道轨迹规划又是近几年智能车辆研究的重点与难点。

针对换道轨迹规划中的安全性问题，Lee等[3]提出一种碰撞避免/缓解系统，可以快速评估主车与周围所有车辆相关的风险，并在面临危险情况时将主车行驶至更安全的区域，但该方法只适用于直道场景。Kim等[4]将行驶的所有区域划分为动态安全区域与潜在危险区域，在安全区域内找到风险值最小的一条轨迹，但未考虑主车与障碍车的体积因素对安全性的影响。倪捷等[5]以目标车道后车的最大减速度和平均减速度为衡量指标，运用SVM(支持向量机)理论建立换道安全性预测模型分析换道行为对道路交通安全的影响程度，对于危险换道行为可以做出较为准确的预测，该方法需要大量的测试数据集来训练模型以达到预测的目的。张荣辉等[6]通过五次多项式确定换道轨迹，在多条候选曲线中基于设定的避撞准则筛选曲线簇，但未考虑当前车道前车对换道行为安全性的影响。唐斌等[7]提出一种基于分段优化的智能车辆换道避障轨迹规划方法，并结合轨迹平顺性、利他性和行驶效率等构建综合评价体系得出最优轨迹，该方法的障碍风险评价函数仅由各轨迹上的最大风险点进行展开对比，对于最优轨迹的筛选不够全面。Zhang等[8]利用TOPSIS(基于理想解相似性的排序偏好技术)算法求解多目标优化问题，从安全轨迹簇中得到最优变道期望轨迹，但未对车辆的速度及加速度进行规划。

针对换道轨迹规划中的舒适性问题，牛国臣等[9]提出一种基于双五次多项式的智能汽车换道轨迹规划算法，以动态规划换道时间和增加舒适性约束条件来改进五次多项式规划算法，在该基础上结合当前环境和换道始末状态计算出中转状态，并采用两次改进的五次多项式算法避免与前方车辆碰撞，该方法对换道过程中舒适性问题的处理较为简单，仅约束了加速度和冲击度的上下限。Wang等[10]基于最优控制理论提出一种考虑乘员舒适度的速度规划方法，通过在一定的舒适约束下最小化车辆的冲击度来实现提高乘员舒适性的目标，但未考虑加速度对舒适性的影响。Zhang等[11]提出一种自动驾驶汽车在动态交通场景下兼顾舒适性和安全性的行驶轨迹规划方法，通过合理的速度离散方法生成具有G2连续性(曲线的一阶导数和二阶导数连续)的各种光滑候选速度，并将这些候选速度与规划路径相结合得到候选轨迹，通过建立轨迹安全性评价模型和轨迹舒适性模型，对各轨迹的舒适性和安全性进行评价得到最优轨迹，该方法将轨迹规划分为路径规划和速度规划，会忽略一部分运动学和动力学特性，同时使得碰撞分析过程较为复杂。Li等[12]提出一种考虑换道舒适性和效率的时变车道轨迹优化方法，通过量化智能车辆与周围障碍车之间的间距约束，结合换道效率以及舒适性利用目标函数对得到的轨迹进行优化，但未考虑冲击度对舒适性的影响。

综上所述，当前考虑安全性和舒适性车辆换道的研究大致分为3 个步骤：规划出所有备选轨迹，安全性分析，舒适性等约束。然而，现有换道安全性研究在轨迹碰撞分析时考虑的因素较为单一或计算量较大。为使考虑因素更为全面，提高计算效率及准确性，亟需设计一个更为完善的安全性分析模型以提高可靠性。近年来，场论的思想越来越多的应用到交通流领域，其借鉴了人工势场法的思想，将交通环境中各位置的风险值以场强来表示。同时，障碍物的外形以及主车与障碍车的相对速度等因素均考虑其中。为了直观且合理地构建安全性分析模型，本文引入风险场模型，将风险场场强作为安全性评价指标，可使碰撞风险进一步降低。当前对于车辆换道轨迹规划的研究也很少综合考虑轨迹的平滑性、安全性、换道效率以及乘员舒适性。针对上述问题，本文提出一种基于风险场评估轨迹的二次筛选方法。为简化计算量，提高算法的实时性，在Frenet 坐标系下规划出所有换道轨迹；通过车辆动力学特性和三圆碰撞模型对轨迹进行初步筛选，根据安全性评价指标、换道效率及舒适性指标建立轨迹质量评价函数，以实现规划出安全和舒适的换道轨迹的目的，最终通过多场景仿真验证所提方法的可靠性。

1 轨迹模型构建

1.1 Frenet坐标系

Frenet 坐标系在自动驾驶领域被广泛使用，特别在弯道场景下的轨迹规划中可以简化求解过程。不同于笛卡尔坐标系，Frenet 坐标系的横、纵轴不是固定不动，其纵轴为规划开始之前选定的参考线，横轴随着纵轴曲率的变化而变动。

如图1 所示，笛卡尔坐标系的横、纵坐标轴为相互垂直的直线X,Y。在Frenet坐标系中，选定参考线为基准，一般以道路中心线作为参考线，本文将规划时刻主车所在车道的中心线选为参考线。假定沿参考线的方向为纵轴S，以垂直于参考线的方向为横轴D。其中，S坐标表示车辆沿参考线方向移动的距离，从参考线的起点s=0 开始。相对于参考线的横向位移用d表示，其绝对值为车辆当前位置到参考线投影点的长度，其正负值由车辆与参考线的相对位置决定，一般取车辆在参考线左侧时为正，反之为负。参考线上投影点的位置由车辆当前位置到参考线最短的垂线段确定。

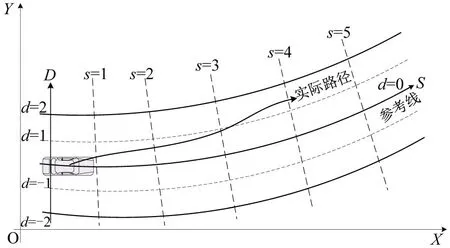
图1 笛卡尔坐标系与Frenet坐标系下的车辆运动Fig.1 Vehicle motion in Cartesian coordinates and Frenet coordinates

1.2 车辆信息的坐标转换

车辆在Frenet 坐标系中的轨迹规划结果需要转换至笛卡尔坐标系中，以供后续可视化过程。如图2所示，车辆位置信息在笛卡尔坐标系中表示为(x,y)，在Frenet 坐标系中用横向位移d和纵向位移s来表示，两者的关系为

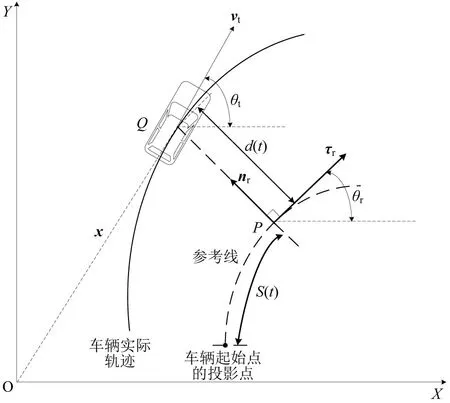
图2 坐标转化Fig.2 Coordinate transforming

式中：x=(x,y)为车辆的质心Q在笛卡尔坐标系下的坐标；s(t)为t时刻车辆在Frenet坐标系中的纵向位移，即车辆在参考线上所对应的投影点P距离起始点的弧长；d(t)为t时刻车辆在Frenet 坐标系中相对于参考线的横向位移，即车辆质心Q与投影点P的距离|PQ|。图中τr为投影点P处的切向量，nr为投影点P处的法向量。

任意时刻t，车辆的位置、加速度等信息在笛卡尔坐标系中的描述为[xt,yt,θt,vt,at,κt]，在Frenet坐标系中的描述为笛卡尔坐标系和Frenet坐标系中各参数及其对应的含义如表1所示。其中，αt为x在Q处的切线转角，st为x在Q处的弧长。

表1 笛卡尔坐标系和Frenet坐标系中各参数及含义Table 1 Parameters and their meanings in Cartesian coordinate system and Frenet coordinate system

综合公式推导，可得Frenet坐标系中车辆的位置、速度、加速度等信息转化为笛卡尔坐标系中车辆的位置、速度、航向角等信息的表达式为

式中：(xr,yr)为投影点P在笛卡尔坐标系下的坐标；θr为投影点P的切向量τr与水平线的夹角，由式(2)亦可得到在笛卡尔坐标系下的车辆信息转化为Frenet坐标系下车辆信息的表达式。

1.3 运动轨迹簇生成

智能车辆的轨迹规划需要满足多个约束，包括车辆运动特性、交通环境动态性和道路形状。为确保车辆底层控制系统的顺利执行，轨迹的曲率和加速度关于时间的一阶导数需要连续。为描述车辆运动轨迹，可使用不同阶次的多项式，如三次、五次和七次多项式。

三次多项式规划的轨迹在位置和速度方面具有一定的平滑性，但无法明确指定加速度的边界条件，而且平滑性受到车辆运动学和惯性负载的影响。在某些情况下，可能需要使用更高阶次的多项式来提高轨迹的平滑性，但这会增加计算时间。随着轨迹阶次的增加，轨迹规划用时就会加长，利用七次多项式规划轨迹时的计算量远大于三次多项式和五次多项式规划轨迹时的计算量。采用五次多项式描述轨迹可以满足加速度的连续性要求，通过六个边界条件来建立车辆位置、速度和加速度的关系，可以提供较为平滑的运动轨迹。

综合考虑轨迹质量和规划效率，采用五次多项式进行自动驾驶车辆的换道轨迹建模是一种相对较佳的选择，因此，车辆的横向轨迹表示为

式中：a0、a1、a2、a3、a4、a5为待定系数，由车辆的始末状态来确定。设定t0时刻为初始位置，在此时刻车辆的横向位移、横向速度和横向加速度分别为，即，因此有

tf时刻为终端位置，此时刻车辆的横向位移、横向速度和横向加速度分别为，即Df=，因此有

当t0=0 时，可以得到令T=tf-t0，则a3，a4，a5之间关系为

由式(6)可以计算出所有参数，得到横向轨迹集合。纵向轨迹的求解与横向轨迹求解方法一样，同上可得到纵向轨迹集合。基于五次多项式生成的多条待选轨迹的横、纵向轨迹如图3所示。

图3 横、纵向轨迹图Fig.3 Lateral and longitudinal trajectory diagrams

2 风险场模型构建

为实现在规划阶段预测轨迹的安全性，同时将换道风险量化为交通环境中各位置的风险值，结合舒适性和换道效率的评价指标综合判定经过初次筛选后的轨迹优劣以得到最佳轨迹。参考人工势场理论，建立行驶过程中交通环境的风险场模型，该行驶风险场综合考虑了障碍车的外形尺寸和主车与障碍车的相对运动。其中，在规划车辆轨迹时，静态风险场考虑车辆的静止状态，静态风险场场强受主车和障碍车之间的相对位置以及障碍车外形尺寸的影响；动态风险场考虑车辆在规划时刻的运动状态，动态风险场场强由主车和障碍车的相对运动来决定。

2.1 静态风险场

静态风险场强度受两个主要因素影响：首先是主车与障碍车之间的相对距离，相对距离越小，碰撞的可能性越大，故静态风险场的场强会增大；其次是障碍车的外形尺寸，大的障碍车在静态风险场中具有更大的影响。

通常情况下，车辆在纵向方向上的速度远高于横向方向上的速度，这是由车辆性能和道路交通特点所决定的。因此，在交通环境中，障碍车在纵向方向上的静态风险场影响范围更广，而在横向方向上的影响范围较小。这就要求为障碍车的纵向尺寸系数分配更高的值，以更好地反映实际情况。

为计算行车过程中的静态风险场场强，采用二维高斯函数。然而，考虑到车辆外形尺寸较大，简单一阶中心距的二维高斯函数不太适用。因此，采用高阶中心距的二维高斯函数，这样可以更好地描述风险场。高阶中心距会展平函数的峰值，从而使整个障碍车的表面都具有相近的风险场强度。主车与障碍车均为静止状态时，交通环境中任意位置的静态风险场场强Usta及各参数的计算公式为

式中：(sx,dx)为交通环境内某一点在Frenet坐标系下的坐标；(sobs,dobs)为障碍车的质心在Frenet 坐标系下的坐标；A为场强系数，β为高阶系数；σs和σd为障碍车的外形函数；Lobs为障碍车纵向方向的长度，本文取Lobs=L=4.2 m；Wobs为障碍车侧向方向的长度，本文取Wobs=W=1.8 m；kd和ks分别为障碍车的横、纵向尺寸系数。各参数取值如表2所示[13]。

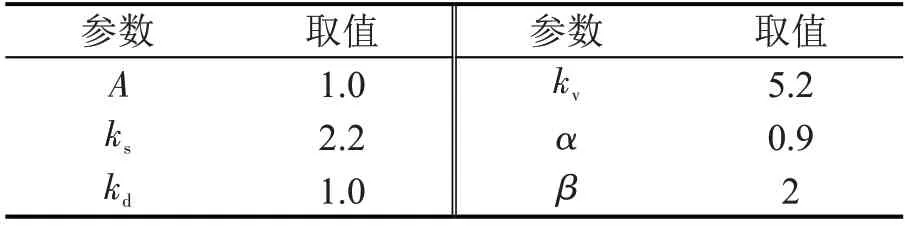
表2 风险场参数Table 2 Parameters of risk field

以某一交通场景为例，在Frenet 坐标系下，设置主车的前方和目标车道后方障碍车的纵向速度均小于主车，且障碍车的横向速度为0，横、纵向加速度均为0。该场景下的静态风险场如图4 所示，前方障碍车为障碍车1，目标车道后方障碍车为障碍车2。静态风险场在障碍车的纵向方向上具有更大的影响，越接近障碍车质心，静态风险场的场强越大。对于靠近障碍车边缘的点，风险场的强度接近其最高点，这意味着整个障碍车表面的风险场强度都相对较高，使用高阶中心距的二维高斯函数构建的静态风险场基本满足要求。

图4 静态风险场Fig.4 Static risk fiel d

2.2 动态风险场

构建动态风险场时，需要综合考虑主车和障碍车的运动情况。动态风险场的场强受到4 个因素影响：主车与障碍车之间的相对距离，相对速度的大小，相对速度的方向以及主车相对于障碍车的朝向。当主车与障碍车的相对速度方向和主车相对于障碍车的朝向相同时，如果相对距离越小，相对速度的绝对值越大，那么发生碰撞的可能性就越高，因此动态风险场的场强就越大。

为满足以上要求，本文以二维高斯函数为基础建立动态风险场。主车在行车过程中各位置的动态风险场场强Udyn及各参数的计算公式为

式中：σv为描述障碍车与主车相对速度的函数，是判断障碍车与主车是否存在相对运动的指标；obs为障碍车的纵向速度；为主车的纵向速度；kv为速度系数；Krel为描述障碍车与主车相对运动方向的变量，α为相对速度系数。kv和α取值如表2所示。

该场景下的动态风险场如图5所示，当主车与障碍车相对距离相同时，动态风险场的场强随着相对速度绝对值的增大而增大。动态风险场的峰值小于场强参数A，且相对速度绝对值越大，动态风险场场强的峰值越大。这意味着随着主车与障碍车之间速度差异的增大，动态风险场将更加突出地反映潜在碰撞的风险。另外，动态风险场的场强最强点并不一定出现在障碍车质心处，会根据多个因素进行动态调整，包括主车和障碍车的相对速度、相对距离以及障碍车的尺寸。这意味着动态风险场的强度会根据这些因素的变化而变化，不一定局限于车辆的特定位置，构建的动态风险场基本满足要求。

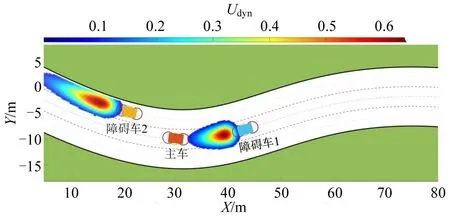
图5 动态风险场Fig.5 Dynamic risk field

2.3 总风险场

车辆总风险场为静态风险场与动态风险场的叠加，即每一点的场强为该点的静态风险场场强与动态风险场场强的合值。

总风险场如图6 所示，可知，前方障碍车与主车的纵向相对速度朝向主车，因此前方障碍车相当于在“靠近”主车，目标车道后方障碍车与主车的纵向相对速度背向主车，因此后方障碍车相当于逐渐“远离”主车。交通环境中所有轨迹点的总场强将作为评价该点的风险指标，场强越高则风险值越高，该值为轨迹二次筛选时的安全性指标。

图6 总风险场Fig.6 Total risk field

3 最佳轨迹选择

3.1 轨迹初筛

车辆在行驶中有其动力学和运动学的极限，为在轨迹规划中降低计算负担、提高规划效率，进行轨迹初筛，筛除那些无法满足车辆极限条件的轨迹。将横、纵向轨迹簇耦合为运动轨迹且对所有轨迹进行排序，并将车辆信息转化至笛卡尔坐标系下。初筛过程包括对曲率、速度、加速度的检查，其通过条件为

式中：κk为轨迹i按照ΔT作离散化所对应的曲率；N为离散化轨迹后的轨迹点数量上限，与采样间隔ΔT以及初始配置、目标配置相关，为减少规划时的计算量，同时保证所规划轨迹的可靠性，纵向位移每间隔约10 m取一个采样点[7]，本文按车辆中速行驶工况将采样间隔ΔT取0.5 s；κmax为最大曲率，根据车辆转弯特性取值为0.2 m-1；vk为轨迹i按照ΔT作离散化对应的速度，根据道路法规以及车辆性能，最高车速vmax取值为30 m·s-1；ak为轨迹i按照ΔT作离散化对应的加速度，根据车辆动力学特性，最大加速度amax取值为5 m·s-2。

此外，为筛除更多不合格轨迹，以减少后续最佳轨迹筛选时的计算量，在轨迹初筛阶段加入三圆碰撞检测。为在处理车辆外形时平衡计算速度和准确性，可以使用多个圆形来近似描述车辆的外形。这种方法可以在一定程度上简化计算，在判断车辆有无碰撞风险时，仅需要通过计算主车与障碍车之间有无近似圆相切或相割，相较于将车辆外形近似为矩形，能大大提升碰撞检测效率。考虑道路尺寸有关规范以及仿真场景下的车速等因素，决定将主车和障碍车的外形用3 个大小相同的车形近似圆表示。车辆三圆碰撞模型如图7 所示，其中，ncir表示车形近似圆的个数，本文取值为3。虚线矩形近似表示车辆外形轮廓，各个实线圆形即为车形近似圆。圆心按从车尾向车头的次序编号为C1，C2，C3，其中C2的圆心为主车和障碍车外形的几何中心。车形近似圆半径Rcir和圆心距dcir由几何关系可得到，即

图7 车辆三圆碰撞模型Fig.7 Vehicle three-circle collision model

主车以及障碍车选用同款车，车身长L=4.2 m，宽W=1.8 m，质心到前轴的轴距Lf=1.6 m，质心到后轴的轴距Lr=1.2 m，计算可得车形近似圆半径Rcir=1.1 m。

对于三圆碰撞检查，其通过条件为

式中：Ckm为主车的3个车形近似圆的圆心，m取值为{1,2,3} ；Ckn为两辆障碍车的6 个车形近似圆的圆心，n的取值为{1,2,3,4,5,6} ；lsafe为行车安全预留距离，本文取lsafe=0.2 m。

3.2 轨迹二次筛选

在每次轨迹规划中，通过数学求解得到一系列实时的轨迹选项，这些轨迹包含了车辆在时空中的位置、速度和加速度等信息。不过，轨迹的初步筛选只考虑了车辆特性和道路规则，忽略了换道轨迹的安全性、舒适性和效率等因素。因此，需要进行第二轮轨迹筛选，将经过初筛的轨迹进行重新排序，综合考虑安全性等多方面因素建立总损失函数为

式中：j为经过初筛后的候选轨迹序列号；Jlat、Jlongi分别为评估换道轨迹舒适性的横、纵向损失加权项；Jt为评估换道效率的损失加权项；JU为评估换道轨迹安全性的损失加权项；ωlat、ωlongi、ωt、ωU为权重系数，它们与各加权项组合影响损失函数，而损失函数影响最佳轨迹的筛选，决定车辆的速度、加速度、冲击度等运动特性。

表示车辆的横向冲击度，可以用来评价轨迹的横向舒适性。横向舒适性损失加权项Jlat定义为在起始时间段t0∼tf的积分，即

式中：ωjerk为冲击度的权重系数。

Jt为换道效率，表示换道过程所需时间，Jt=tf-t0；安全性损失加权项JU定义为交通环境中的总风险场场强U(t)在t0∼tf时间段的积分，即

由换道安全性和舒适性目标，确定权重系数ωlat、ωlongi、ωt、ωU、ωjerk分别[14]为1.0，2.0，1.0，0.2，0.01。

4 仿真分析

为充分验证上述轨迹规划算法的实时性和有效性，本文利用Matlab 对算法进行编程，并设计双车道的弯道平路面对所提出的换道轨迹规划方法进行仿真验证。由于换道风险值更多取决于主车与障碍车的相对速度，因此，将换道起始时刻主车与障碍车的位置固定，不同场景设置障碍车不同速度和加速度，以图8 所示的交通场景共构建3 个场景。车辆以Hx为索引，其中主车的Hx为0，前方障碍车的Hx为1，左后方障碍车的Hx为2。

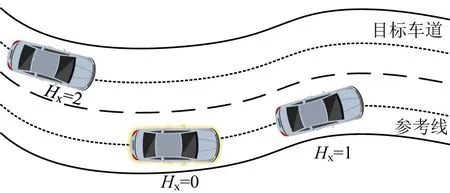
图8 交通示意图Fig.8 Traffic diagram

场景1中，主车道前方障碍车和左后方障碍车与主车以相同的纵向速度行驶；场景2 中，两辆障碍车以较小的纵向速度行驶；场景3为紧急避障工况，前车减速，左后方障碍车匀速行驶。将主车道中心线作为参考线，3 种场景中主车的纵向速度均为14 m·s-1，主车与前、后方障碍车的横向速度与横向加速度均设置为0。每辆车的位置、纵向速度和纵向加速度等数据如表3所示。

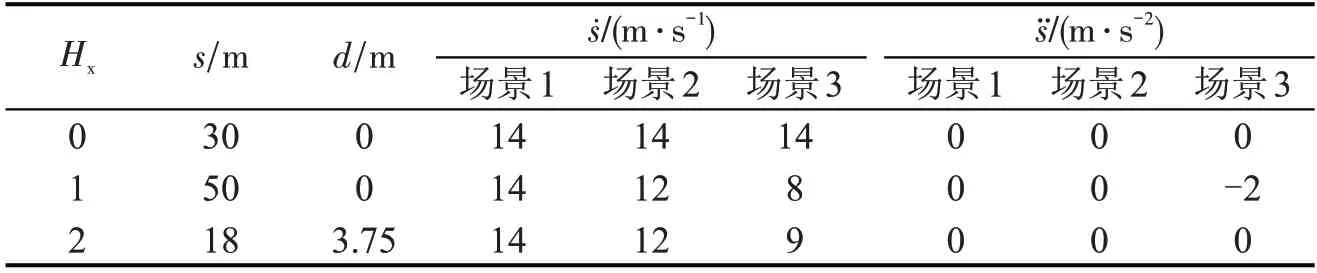
表3 主车与障碍车数据Table 3 Data on main vehicle and obstacle vehicle

4.1 换道行为的安全性分析

因3个场景下各车辆的起始位置均相同，基于五次多项式规划出来的所有换道轨迹均为288条。场景1中，通过轨迹初筛剔除不合格轨迹256条，其中未通过三圆碰撞检测的轨迹有20 条，余下32 条候选轨迹以供轨迹二次筛选；场景2 中，通过轨迹初筛剔除不合格轨迹256条，其中未通过三圆碰撞检测的轨迹有20 条，余下32 条候选轨迹以供轨迹二次筛选；场景3 中，通过轨迹初筛剔除不合格轨迹244条，其中未通过三圆碰撞检测的轨迹有8条，余下44条候选轨迹以供轨迹二次筛选。

车辆在3 个场景下轨迹二次筛选的换道风险值和总损失函数值如图9所示。

图9 最佳轨迹序列选择Fig.9 Selection of optimal trajectory sequence

3个场景均对比了考虑风险场和不考虑风险场两种情况下的最佳轨迹序列选取：如图9(b)所示，场景1的最佳轨迹序列号为10，第10号轨迹的换道时间为4 s；如图9(d)所示，场景2 的最佳轨迹序列号为18，第18 号轨迹的换道时间为4.5 s；如图9(f)所示，场景3 的最佳轨迹序列号为6，第6 号轨迹的换道时间为3.5 s。对比图9(c)和图9(e)可知，当减小前方障碍车纵向速度且将纵向加速度设置为负值时，主车前方相同位置的风险场场强会变大，所有换道轨迹的风险值将变大。同时，图9(f)中的总损失函数值整体大于图9(d)中的总损失函数值。

智能车辆在3 个场景下的完整换道轨迹如图10 所示。可以看出，主车在换道过程中与前方障碍车以及目标车道的左后方障碍车预留有较大的安全距离。

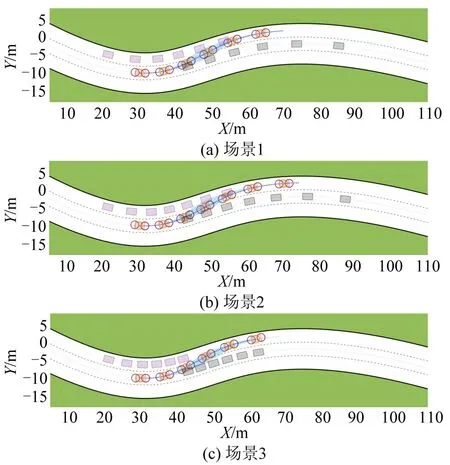
图10 车辆完整换道轨迹Fig.10 Complete lane change trajectory of vehicle

4.2 换道行为的舒适性分析

由于当前行车舒适性的研究只考虑平面运动也就是横、纵向的位移以及绕竖直方向的旋转，不考虑垂直方向的震动对舒适性的影响。车辆的横、纵向加速度对乘员舒适性的影响如表4所示[15]。同时，人体舒适性的冲击度阈值为0.3g，g近似取为9.8，在此范围内均认为舒适。

表4 车辆加速度与乘员舒适度关系Table 4 Relationship between vehicle acceleration and passenger comfort

3 种场景下换道时车辆的加速度和冲击度如图11和图12所示。

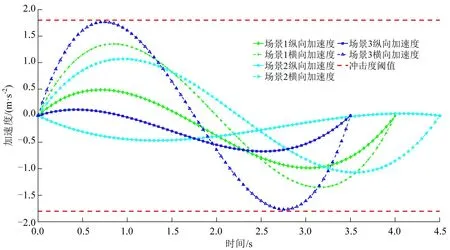
图11 车辆横纵向加速度Fig.11 Lateral and longitudinal acceleration of vehicle

由图11 可知，3 个场景中的主车横、纵向加速度均小于阈值1.8 m·s-2，加速度满足舒适性要求。由图12可知，3个场景中的主车纵向冲击度均小于阈值0.3g，由此可知，在换道过程中，主要考虑横向冲击度对人体舒适性的影响。在场景2中，主车的横向冲击度均小于阈值0.3g，因此，在整个换道过程中均满足舒适性要求；在场景1 中，主车的横向冲击度在换道开始的前0.1 s 以及换道结束前0.1 s 超过阈值，总体换道时间为4 s，95%的换道过程满足舒适性要求；在场景3 中，主车的横向冲击度在换道开始的前0.3 s以及换道结束前0.3 s超过阈值，总体换道时间为3.5 s，82.9%的换道过程满足舒适性要求。综合场景1 和场景2 可知，在正常换道过程中，司乘人员在换道过程中有97.5%的时间感到舒适，总体能满足舒适性的要求。在紧急换道避障的情况下，在保证安全性的前提下，依然能保证换道过程的大部分时间处于舒适状态。

智能车辆在3 个场景下的曲率变化如图13 所示，可以看出3 种场景下的轨迹曲率均在0.000～0.047 m-1之间波动，远小于最大曲率κmax，表明规划出来的换道轨迹的平滑性较好。

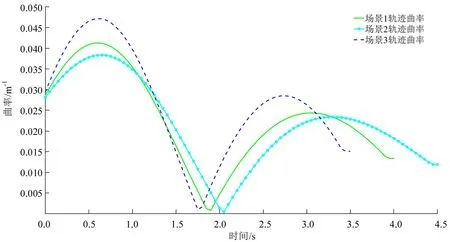
图13 车辆曲率变化Fig.13 Changes of vehicle curvature

5 结论

(1)所提出的换道轨迹规划方法在常规轨迹规划基础上，加入轨迹初步筛选这一步骤，筛除不满足车辆动力学特性以及可能发生碰撞的轨迹，该方法相较于传统的单次轨迹规划方法可以降低规划的算力损耗，提升规划效率。

(2)参考人工势场理论，对交通环境中的障碍车建立行驶风险场模型，综合考虑障碍车的长、宽物理属性和速度、加速度的状态参数，实现主车对环境的风险评估，为换道的安全性评估提供理论基础。

(3)所提方法在满足主车换道的安全性、及时性和舒适性的前提下，规划出的轨迹还具有很好的平滑性，在应对障碍车多种运动状态时具有较好的适应性，包括障碍车不同位置、速度和加速度等。