新型双体波浪能转换装置多自由度耦合水动力特性研究
顾兴远, 牛玉博, 郑 阳, 何培杰, 陈启卷
(1.武汉大学 动力与机械学院,武汉 430072;2.武汉大学 水力机械过渡过程教育部重点实验室,武汉 430072)
在大多数情况下,波浪能的能量密度在离岸较远的位置往往比靠近海岸的位置更高[1-2],但与此同时,离岸较远也使得波浪能转换装置(wave energy converter, WEC)生产的电能难以输送到陆上电网,且安装成本也会因此而提高。如果将WEC与其它海上设备结合,使WEC生产的电能为海上设备供电,可以有效解决这两个问题。因此本文将一种可主动共振的纵摇式WEC[3-4]与海洋浮标相结合,设计出一种新型双体WEC。
目前大多数双体WEC都是双体垂荡系统,即利用两个物体之间的垂荡运动来转换波浪能[5]。Al等[6]通过CFD获取淹没体的黏性阻力系数,再通过动力学建模,研究垂荡双体WEC中水下物体的不同形状的特性,但仅考虑了垂荡运动,且鉴于双体距离较远而忽略了双体之间的辐射力影响。Ma等[7]结合Fortran编程与AQWA软件,分析了垂荡双体WEC的频域水动力性能和时域运动特性,但忽略了其它自由度的运动。周亚辉等[8]对穿孔式双浮体装置开展频域仿真,研究垂荡双体的特性,同样忽略了垂荡以外的运动。对垂荡双体WEC的建模研究,往往仅考虑垂荡这单一自由度,而忽略其它自由度的影响。Dai等研究一种新型双体WEC,主体为由绳索连接的两个球体,同时对双体的垂荡、纵荡、纵摇运动开展研究,但考虑到装置为球体,忽略了黏性影响,此外还忽略了两个物体运动产生的辐射力对其它自由度的影响,即未计及各自由度之间的耦合。Tran等[9]同时考虑了黏性以及各自由度之间耦合,对一种圆柱体式的单体WEC开展了水动力性能研究。对多自由度的双体WEC的建模研究,往往通过简化装置外形等方式忽略黏性以及各自由度之间耦合的影响,从而避免模型过于复杂。
本文提出的新型双体纵摇WEC的外形较为复杂,因此对该装置的建模仿真中同时考虑了双体各自由度耦合以及黏性影响。首先通过AQWA开展频域仿真,计算装置的水动力参数;通过理论推导,在同时考虑双体多自由度耦合以及黏性影响的情况下建立时域模型,并将AQWA仿真获取的水动力参数代入时域模型,分别开展规则波、不规则波的仿真,分析质心位置、PTO阻尼大小对装置发电性能的影响,根据真实海况划分若干不规则波并分别开展仿真,研究装置在真实海况下的发电性能。
1 装置设计
本文提出的新型波能装置由两部分组成:一部分是漂浮在水面上的圆盘形浮标,另一部分是重力与浮力相等的可调节质心的摆体,如图1所示。

图1 新型双体WEC
支架上端与海洋浮标固定,下端的横轴穿过摆体,使得摆体可绕横轴转动。摆体内部密封有配重、配重调节机构、PTO机构。配重位置调节机构可控制配重升降,从而调节摆体的质心位置。PTO机构可将摆体与横轴之间相对转动的机械能转化为电能。装置在工作时,浮标漂浮在水面,而经过设计的摆体受到的重力与浮力相等,完全淹没在水下,因此可减少风浪冲击和能量辐射,同时减小自由表面黏性带来的影响。相比于将PTO机构安装在海床上的单体WEC[10],新型双体WEC更容易维护。
2 水动力建模
此前研究人员对双体WEC的建模尚未见同时考虑双体各自由度耦合以及黏性影响的情况,因此本节将详细推导新型双体纵摇WEC的水动力模型。
2.1 势流理论
以垂荡运动为例,波浪与物体相互作用的控制方程可表示为
(1)
式中:m为物体质量;g为重力加速度;p为作用在物体上的流体压强;S为物体的湿表面;z为物体在垂荡方向的位移,正方向向上;Fother为包括PTO力在内的其它作用力的合力。
为进一步表达等式右侧各项,引入线性势流理论,入射流体作用在装置表面的总压强pa可由Bernoulli方程计算为
(2)
式中:ρw为海水密度;zs为湿表面面元位置;φt为入射流体的总速度势。
根据线性势流理论,入射流体的总速度势φt可表示为三部分
φt=φI+φdif+φrad
(3)
式中,φI,φdif和φrad分别为装置不存在时入射波的速度势、由于装置存在导致的衍射波的速度势和装置运动导致的辐射波的速度势。
将式(3)代入式(2),应用线性势流理论忽略二次项,将各面元压强沿湿表面积分,可得波浪-物体相互作用的控制方程
(4)
式中:Fe为波浪激励力;Fr为辐射力;Fres为回复力;FPTO为PTO力。
2.2 运动方程
如图2所示,设A为浮标与摆体的连接轴中心,B为浮标质心,C为摆体壳质心,D为配重质心,P为摆体整体的质心。
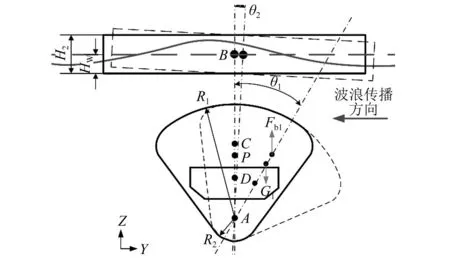
图2 装置简图
忽略横荡、艏摇、横摇运动,只考虑装置的纵荡、垂荡、纵摇运动,将这三种运动的方向分别记为Z、Y、RX方向,于是装置的运动共四个自由度,分别是装置整体的纵荡、装置整体的垂荡、摆体的纵摇、浮标的纵摇。根据Lagrange力学理论,将yA、zA、θ1和θ2作为广义坐标,其中yA、zA为连接轴中心位置,θ1为摆体的转角,θ2为浮标转角,以顺时针为正方向。于是A点在惯性系中的坐标为
A=(yA,zA)
(5)
则P、B点在惯性系中的坐标可表示为
r1=p=(yA+L1sinθ1,zA+L1cosθ1)
(6)
r2=B=(yA+L2sinθ2,zA+L2cosθ2)
(7)
式中,L1、L2分别为AP、AB长度。根据Lagrange方程,系统的时域运动模型可表示为
(8)
式中:qj为广义坐标;T为动能;Qj为广义力。广义力的定义为
(9)
式中:Fv为外力;rv为外力作用点的位置矢量。将外力作用点移至A点,合外力在Y方向、Z方向的分量分别为Fy、Fz,合外力作用在摆体、浮标上的扭矩分别为M1、M2。将式(9)代入式(8),对式(6)、式(7)求导得到速度,再根据动能定理,可得装置四个自由度的运动方程
(10)
式中:m1,m2分别为摆体、浮标的质量;L1,L2分别为摆体、浮标的质心到转动轴的距离;v1,v2分别为摆体、浮标质心的速度;J1,J2分别为摆体、浮标绕质心的转动惯量;ω1,ω2分别为摆体、浮标的角速度。根据势流理论,Fy、Fz、M1、M2分别可表示为
(11)
式中,MPTO为PTO力矩,各下标的含义为:1为力作用于摆体,2为力作用于浮标,y为力作用于Y方向,z为作用于Z方向,r为辐射力,e为波浪激励力,b为浮力,d为黏性力。
波浪激励力可表示为
(12)
式中:下标i(i=1, 2) 为受力物体;下标j(j=y,z) 为力的方向;k为波浪激励力系数;β为波浪激励力相角,即波浪激励力与入射波的相位差。
浮力可表示为
(13)
式中:S为浮标底面积;ρw为海水密度;Lb1为摆体浮心与A点的距离;kb2为浮标的水静力刚度。
根据Cummins方程,摆体受到的辐射力可表示为卷积形式
(14)
式中:K(t)为K(ω)的脉冲响应函数,K(ω)由附加质量和辐射阻尼计算得到;下标i(i=y,z) 为力的方向;下标11、21分别为摆体的运动对摆体自身的影响、浮标的运动对摆体的影响,以K11yi为例,表示摆体自身的y方向运动对i(i=y,z)方向造成的辐射力影响的脉冲响应函数。浮标受到的辐射力计算式与摆体类似,仅将下标11、21改为22、12即可得到。
2.3 辐射力卷积近似
时域中的辐射力计算式是以卷积的形式表示的,不便于计算,因此这里采用Realization方法[11],对卷积项进行近似,将卷积项转化为便于计算的状态空间模型
(15)
式中:xr∈n×1为辐射力的状态向量,Ar∈n×n、Br∈n×1、Cr∈1×n为参数矩阵,n为辐射力的状态空间模型的阶数,阶数越高则状态空间模型对卷积项的近似效果越好,但是需要更多的计算资源。
2.4 黏性力模型
WEC一般尺寸较小,黏性损失较明显,因此有必要将黏性力引入到模型中做修正,本文采用Morison方程计算黏性力
(16)
式中:Sw为装置的特征面积;Cd为装置的黏性阻力系数;v为参考点处流体质点的速度,参考点选择为物体竖直中线上各自高度的一半位置处,因此浮标、摆体的参考点分别为水面下0.5 m、4.5 m。根据Airy波浪理论,对于规则波
ζ=Acosα
(17)
参考点处流体的流速v可表示为
(18)
式中:ω为波浪频率;ht为参考点深度;k为波数,满足色散关系式
(19)
对于不规则波,参考点处流体的流速为各频率子波在该点的流速之和。
3 仿真与分析
3.1 仿真对象
以典型的10 m直径海洋浮标为载体,设计装置的具体尺寸、质量等参数如表1所示。

表1 装置设计参数
如图2所示,摆体外轮廓由上下两个60°的圆弧与两侧的曲线构成,R1为上部圆弧的半径,R2为下部圆弧的半径[3],W为摆体沿横轴方向的宽度。D为浮标的直径,H2为浮标的厚度,Hw为浮标淹没深度,m1为摆体含配重的总质量,m2为浮标的质量,mt为配重的质量,J1s为摆体无配重时的转动惯量,J2为浮标的转动惯量,Jt为配重的转动惯量,转动惯量均为纵摇方向的值,参考轴在物体各自质心处。配重位置可调节范围为0~0.8 m。
3.2 水动力参数计算
本节通过ANSYS AQWA软件开展频域仿真,计算WEC的辐射阻尼、附加质量和波浪激励力系数等水动力参数。
为避免网格密度对计算结果的影响,本文对于浮标-摆体结构建立三个密度不同的网格进行仿真,进行网格无关性检验,结果表明,网格节点数为1 015时的仿真结果与网格节点数为3 355的结果略有差别,而当网格节点数增大到11 823时,仿真结果与网格节点数为3 355时的基本相同,可认为此时网格节点数继续增大也基本不会对计算结果的准确度造成影响,因此最终选用11 823个网格节点的仿真结果。
图3为水动力参数的计算结果,其中kr为辐射阻尼。由于与辐射力相关的水动力参数(辐射阻尼、附加质量)包含大量双体各自由度之间的耦合项,在图3中只展示其中一部分。可以看出,摆体运动对浮标所受的辐射力的影响较小,明显小于浮标对摆体的影响。

图3 双体纵荡运动在RX方向产生的辐射阻尼
部分辐射力参数(辐射阻尼、附加质量)的值基本为0,具体包括:纵荡产生的辐射力参数在Z方向的分量,垂荡产生的辐射力参数在Y、RX方向的分量,以及纵摇产生的辐射力参数在Z方向的分量。根据Falnes的理论,对于对称物体,根据其对称平面的特征,有部分的辐射力参数基本为0[12],而摆体与浮标均有x=0以及y=0这两个对称面,因此存在大量等于0的辐射力参数。忽略部分参数,最终保留20个辐射力参数分别进行卷积的状态空间模型近似。
3.3 黏性力参数计算
对于本文中浮标外形的扁圆柱体,纵荡、垂荡、纵摇方向的黏性阻力系数分别取为CdY2=1,CdZ2=1,CdRX2=0.2。由于摆体在纵荡和垂荡方向上近似横置的扁圆柱体,同样分别取CdY1=1,CdZ1=1。对于摆体的纵摇方向的黏性阻力系数,可以通过CFD的自由衰减振荡仿真获得[13]。
本文通过Fluent对摆体单体的自由衰减振荡过程开展二维的CFD仿真,最终得到摆体纵摇方向的黏性阻力系数为CdRX2=0.213 3。图4为三种模型(CFD、加入黏性项的非线性模型、无黏性的线性模型)的仿真结果,设定摆体的初始释放转角为50°。结果表明,加入黏性项后与CFD仿真结果拟合较好,明显优于无黏性模型。同时也验证了模型的可靠性,能够以此模型开展后续仿真研究。
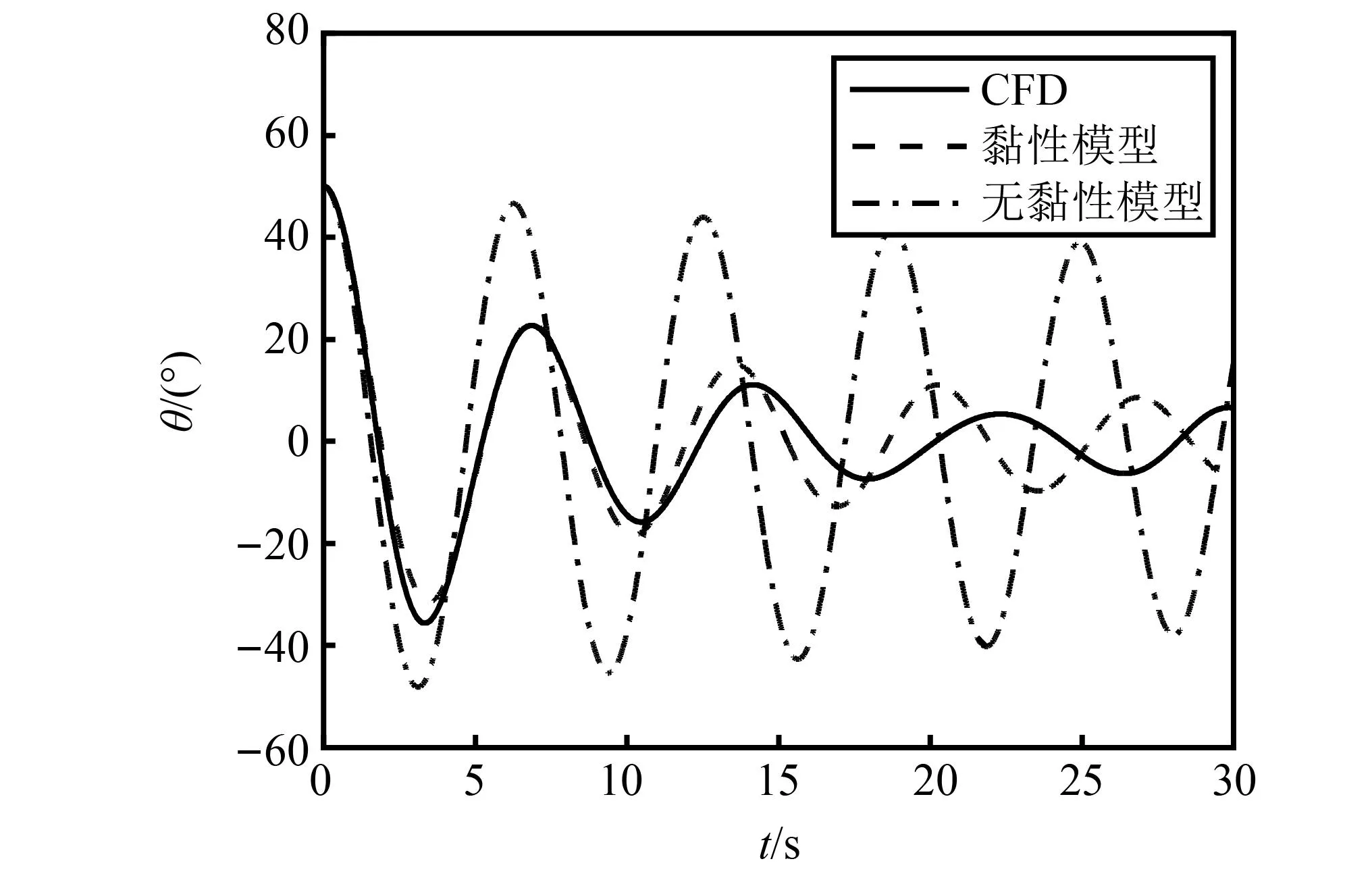
图4 摆体自由衰减振荡
3.4 规则波仿真
3.4.1 固有周期
为了研究在规则波作用下,装置的运动与发电性能,将规则波代入前述建立的四自由度耦合非线性模型中开展仿真。
已有研究表明,对于以单个摆体作为俘能装置的纵摇式WEC,通过改变其内部配重的质量分布,可以显著影响其固有周期,通过控制固有周期与波浪周期一致,能够使WEC与波浪共振,从而有效提高WEC的发电能力。对于本文的浮标与摆体结合的双体WEC,有必要研究调节摆体内部配重的质量分布对装置整体的发电性能所带来的影响。
通过改变配重位置,可以改变摆体的质心位置、转动惯量,从而改变摆体的固有频率,摆体纵摇方向固有频率的具体表达式为
(20)
式中:ωin,Keq,Jeq分别为摆体的固有频率、等效刚度和等效惯量;Fb1为摆体的浮力;lb1为摆体浮心到连接轴中心的长度;Jadd1为摆体的附加质量,其值与摆体的固有频率有关,可以通过迭代运算得到固有频率。摆体的固有周期Tin可由固有频率计算得到。摆体固有周期4~7 s对应配重位置范围为0.070~0.595 m。
3.4.2 参数响应

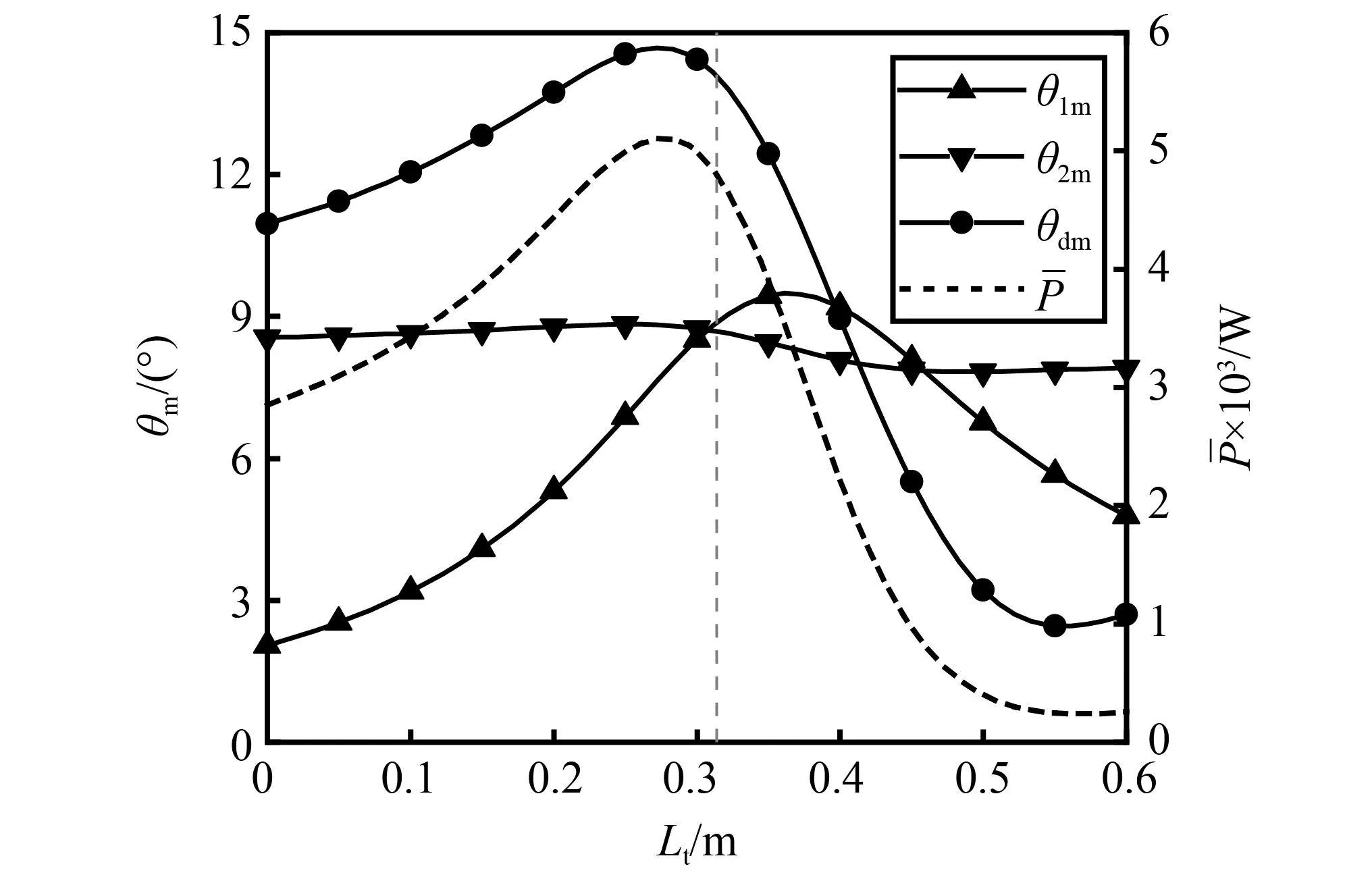
图5 规则波(T=5 s, H=1 m)下配重位置对装置的影响
图5的结果表明,随着配重位置的上移,θ1m、θdm会先增后减,而θ2m变化较小。装置发电功率的变化趋势与θdm相似,二者均在配重位置接近0.314 m时达到峰值,可见调节摆体内的配重位置对装置整体的发电功率影响显著。
PTO阻尼对于振荡体式WEC的发电能力的影响同样显著,对于单体、单自由度的WEC装置,已有理论可以计算其最优PTO阻尼kopt,具体公式为
(21)
式中,kr为辐射阻尼;J为物体转动惯量;Ja为附加质量;cPTO为PTO刚度;Fb为浮力;Lb为浮心到转动轴的距离;G为重力;L为质心到转动轴的距离;ω为波浪角频率。根据式(21)计算可得,单自由度的摆体在5 s周期的波浪下的最优PTO阻尼为2.83×104N·m·s/rad。
而对于双体WEC,目前未见有关最优PTO阻尼的计算方法,因此下面研究在规则波作用下,不同PTO阻尼对于装置发电能力的影响。分别设定不同的PTO阻尼开展仿真,结果如图6所示,其中kPTO表示PTO阻尼。
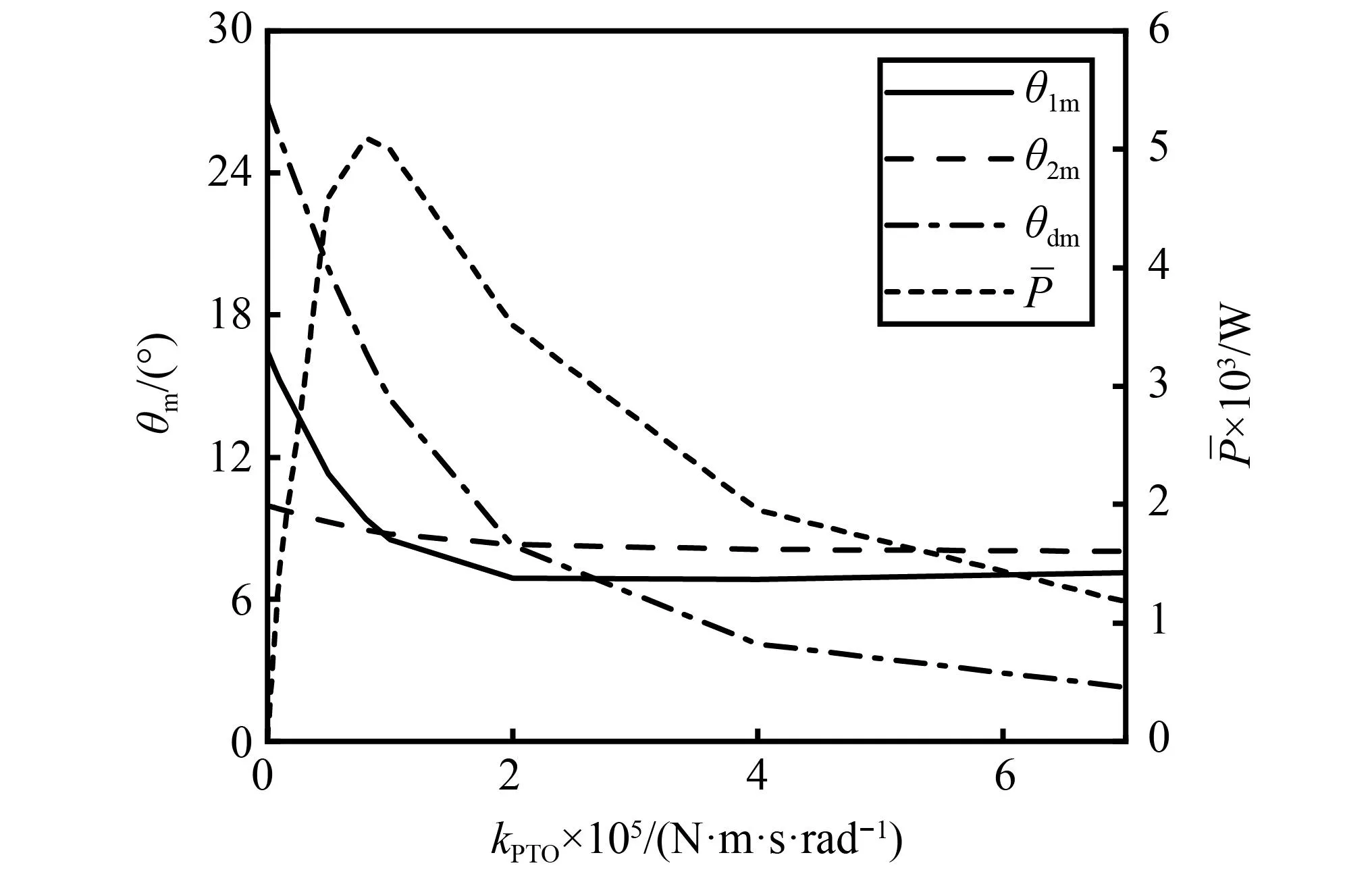
图6 规则波(T=5 s, H=1 m)下PTO阻尼对装置的影响
随着PTO阻尼的增大,θ1m先快速减小,然后趋近于θ2m;而θ2m的变化幅度较小,基本稳定为8°;θdm则快速减小,逐渐趋近于2°。当PTO阻尼约为1×105N·m·s/rad时装置发电功率达到峰值,明显大于单自由度的摆体在5 s周期的波浪下的最优PTO阻尼。
3.5 不规则波仿真
真实海况的波浪并不规则波,而是由频率、波高不同的子波组成的不规则波,因此有必要研究在不规则波作用下,装置的运动与发电性能。
3.5.1 不规则波模型
本文采用标准JONSWAP谱[14]建立实际不规则波的模型,标准JONSWAP谱的表达式为
(22)
式中:Sω为波浪谱密度;Tp为峰值周期;Hs为有义波高,参数σ可表示为
(23)
根据波浪谱,即可以计算任意角频率ω对应子波的振幅A(ω)
(24)
3.5.2 参数响应
由于不规则波与规则波的特性差别较大,有必要进一步研究在不规则波作用下配重位置对装置发电性能的影响。将Hs=1 m,Tp=5 s 的标准JONSWAP谱的不规则波代入四自由度耦合非线性模型中,在初始配重位置不同的情况下,分别开展仿真,结果如图7所示。竖直虚线为摆体固有周期与波浪周期一致时的配重位置(Ltr=0.314 m)。

图7 不规则波(Tp=5 s, He=1 m)下配重位置对装置影响
从图7可以看出,装置在不规则波的作用下,一些特性仍与在规则波的作用下相近:随着配重位置的上移,θ1m、θdm会先增后减,而θ2m变化较小。装置发电功率的变化趋势与θdm相似,二者在相近的位置达到峰值,可见在不规则波的作用下调节摆体内的配重位置对装置整体发电功率的影响依旧显著,为了使装置达到最大的发电功率,对摆体内配重位置的调节可以参考摆体固有周期与波浪周期一致时的配重位置。
而与规则波的仿真结果不同的是:θ1m、θdm在峰值附近变化较为平缓。浮标的转角平均幅值较小,约为5°,而θ1m、θdm均较大,可见在不规则波作用下,浮标十分稳定,不会出现大幅纵摇。
同样地,为研究PTO阻尼变化的影响,分别设定不同的PTO阻尼开展仿真,结果如图8所示。

图8 不规则波(Tp=5 s, He=1 m)下PTO阻尼对平均功率影响
与规则波仿真结果相似的是,随着PTO阻尼的增大,θ1m先快速减小,然后减小幅度逐渐平缓,而θ2m基本稳定在6°。
与规则波仿真结果不同的是,θ1m与θdm相近,当PTO阻尼约为2×105N·m·s/rad 时,装置发电功率达到峰值,且发电功率曲线在峰值附近的变化较为平缓。
3.5.3 真实海况仿真
进一步地,为研究装置在实际海况的发电性能,选取中国东海、南海开展真实海况仿真[15-17],研究装置在不同海域中的性能。
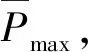
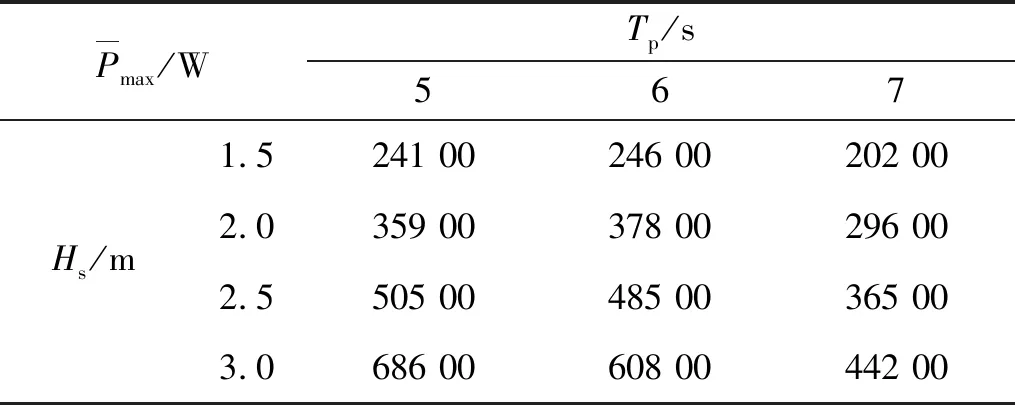
表2 中国东海海况下的最大时均发电功率
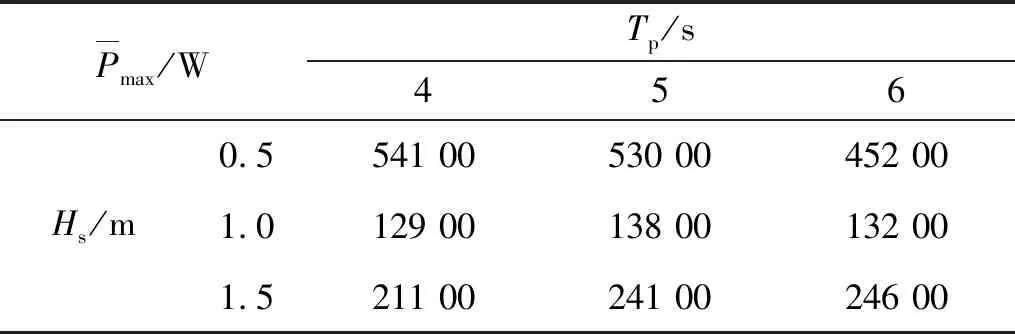
表3 中国南海海况下的最大时均发电功率
俘获宽度比(capture width ratio, CWR)常用于衡量WEC的发电能力,其计算式为
(25)
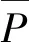
(26)
式中:ρw为海水密度,取1 025 kg/m3; g为重力加速度;Te为不规则波的能量周期,对于本文采用的JONSWAP标准不规则波谱,基本满足Te=0.9Tp的关系。
计算不同波况下装置共振时的俘获宽度比,如图9所示。结果表明,装置共振时的CWR普遍较高,能够较好地俘获波浪能。波高较小时,装置的CWR较高,这表明装置在小波高情况下可以有效利用波浪能量,从而保持一定的发电能力。

图9 俘获宽度比
4 结 论
本文提出了一种将摆体与海洋浮标结合的新型波浪能转换装置,通过AQWA建立频域模型,计算装置的水动力参数,并通过理论推导,建立非线性的时域模型,分别开展规则波、不规则波的仿真,对该装置进行了研究。
通过AQWA开展频域仿真,获得装置的水动力参数,对装置建立四个自由度耦合的时域模型,并在模型中加入非线性黏性项,通过CFD仿真摆体自由衰减振荡,获得了相应的黏性阻力系数,并验证了模型的准确性。
通过多自由度耦合的非线性模型开展时域仿真,研究装置在规则波、不规则波作用下运行时,配重位置以及PTO阻尼对装置的运动状态以及发电功率的影响。结果表明:在不规则波作用下,装置的最优PTO阻尼大于在规则波作用下的最优PTO阻尼,且明显大于单个摆体的最优PTO阻尼;无论是在规则波还是不规则波作用下,调节配重位置都可以使装置发电功率达到峰值,且调节时可以参考摆体固有周期与波浪周期一致时对应的配重位置。
最后,研究装置在真实海况中运行的性能,分别将中国东海、中国南海的海况划分为有义波高、峰值周期不同的不规则波矩阵,并分别优化配重位置,得到装置在各海况的最大功率矩阵。结果表明:装置在周期为4~7 s的波况下发电能力较好,波高为1 m时的平均CWR可达0.54;且装置在小波高情况下也可以有效利用波浪能量,从而保持一定的发电能力。因此装置较为适用于中国东海、中国南海海域。
本文对新型波浪能转换装置的研究可以为海洋浮标等海上设备的供电方式提供参考,并且本文建立的双体四自由度耦合的非线性水动力模型可以为研究人员研究复杂外形的双体WEC时提供参考。在将来的研究中还可以进一步探索系泊系统对装置发电性能的影响。

