平面SV波入射下地上建筑群-地铁隧道群动力相互作用研究

刘中宪, 王建旭, 金立国

(1. 天津城建大学 土木工程学院,天津 300384;2. 天津市软土特性与工程环境重点实验室,天津 300384;3. 中国地震局地质研究所 强震构造与地震危险性研究室,北京 100029)

近年来,随着城市现代化进程的加快,我国城市轨道交通建设飞速发展。双线或多线地铁隧道近距离密集穿越地上建筑群的案例非常普遍。在1995年日本阪神大地震[1]中,大开地铁地下车站的临近地上建筑发生了严重破坏,这引起了大量学者开始关注地铁隧道与邻近地上建筑的动力相互作用问题。目前,地下结构与地上建筑的相互作用研究主要集中在单一隧道与单一建筑物的相互作用问题[2],而对于地上建筑群与地铁隧道群的这种群体性相互作用问题还研究较少[3]。

现有针对地铁隧道与邻近地上建筑地震相互作用问题的研究方法主要有数值方法和试验方法,其中在数值法方面已经积累了很多研究成果[4-15]。如Pitilakis等[16]研究了地铁隧道与单自由度地表建筑物之间的动力相互作用,得出了地上建筑的存在会使隧道的衬砌弯矩和轴力增大的结论,并给出了增大倍数保守值(分别为25%和30%)。王国波等[17-18]对地下结构与邻近地表结构在地震时的相互影响进行了计算总结和归纳。卢致强等[19]采用有限元法并结合国内外既有工程经验,研究了地震作用下地铁隧道与邻近建筑相互影响。结果表明,地震作用时,考虑到周围地层对隧道结构的约束作用,邻近建筑的存在导致隧道结构所受地震作用增强。谢军等[20]同样通过有限元法建立了隧道-土-地表建筑相互作用体系的三维计算模型,对该体系进行地震响应分析。研究了单独在隧道衬砌和土体之间设置橡胶减震层以及单独在地表建筑基础之下设置砂垫层减震层时,减震层厚度对该体系地震响应的影响。Clouteau等[21]基于边界元法,研究了建筑群分布特性对地表地震动特性和结构响应的影响。在试验方法方面,李延涛等[22]以隧道-土体系为研究对象,开展了1∶30的振动台试验。并得出结论:隧道在远场地震作用下的反应较强烈,上隧道的应变反应小于下隧道的应变反应,上、下隧道在拱肩和拱脚处的应变明显大于其他部位。陈国兴等[23]进行了近、远场强地震动作用下软弱粉质黏土场地框架式地铁车站结构体系的大型振动台模型试验。试验结果表明,地震动频谱特性对框架式模型侧墙的变形模式和大小存在显著的影响。地下结构中柱在地震中损伤严重。

目前,我国城市轨道交通的抗震设计并没有考虑周围建筑群的影响。且目前的研究主要集中在地震作用时地下结构-单一地上建筑对彼此抗震性能的影响,很少涉及地铁隧道群与地上建筑群之间的相互作用。因此,对地上建筑群与隧道结构之间的动力相互作用做更深入的研究,已成为城市工程抗震和防震减灾研究的重要内容。

综上,本文采用一种高精度间接边界元法(indirect boundary element method,IBEM)其具有降低问题求解维度、自动满足无限远辐射条件、无高频频散,位移和应力都具有较高计算精度的优点,可快速方便地处理复杂场地条件下的地震波多域散射计算问题。可用来求解地上建筑群-地铁隧道群的动力相互作用问题,此后,进一步参数化分析了双线地铁隧道和地上建筑群在平面SV波作用下的地震相互作用问题。综合考虑了不同入射角度与入射频率,不同建筑物数量和隧道个数等因素对建筑群-隧道群抗震反应的影响,并为工程实践提供了理论依据。

1 计算模型

如图1所示,弹性半空间中有多个地上建筑,在其下方穿过双线隧道。为简化计算,采用剪力墙模型模拟地上建筑,其中地上建筑的基础部分假定为刚性基础。

图1 计算模型

本文以三幢地上建筑为例。半空间区域记为域Θ其域内剪切波速、泊松比和密度分别为β1、μ1、ρ1;隧道衬砌区域分别记为域Ψ1、Ψ2隧道衬砌的材料特性参数记为β2、μ2、ρ2;建筑物的基础区域分别记为域T1、T2、T3其材料特性参数记为β3、μ3、ρ3;其对应的上部剪力墙区域分别记为域Ω1、Ω2、Ω3该区域的材料特性参数记为β4、μ4、ρ4。由于地上建筑的基础被假定为刚性,因此在后续计算中,作者是通过将基础剪切波速β3赋予充分大的数值来实现的。模型中半空间介质、剪力墙介质和隧道衬砌介质,均假定为线弹性均匀各向同性介质。区域Θ和Ψ1、Ψ2交界面记为L11、L13;域Θ和T1、T2、T3交界面分别记为L2、L3与L4;剪力墙Ω1、Ω2、Ω3和基础T1、T2、T3交界面分别记为L5、L6、L7;剪力墙外表面边界分别记为L8、L9、L10。建筑物上部结构高度均为H,基础埋深均为h,隧道圆心距地表距离设为d,隧道圆心之间的距离设为da,隧道内外半径分别为a和a1。

2 计算方法与求解

2.1 波场分析

根据弹性波动理论,总波场可分为自由场和散射场的叠加。半空间域Θ同时受到自由场和散射场作用,隧道域(Ψ1、Ψ2)、基础域(T1、T2、T3)和剪力墙域(Ω1、Ω2、Ω3)内只受到散射场作用。对于自由波场反应的求解可参见文献[24]的波场分析部分。根据单位势理论和IBEM原理,散射场通过在模型表面(L1-L14)离散单元上施加虚拟荷载产生。散射场引起的位移和应力的积分表达式如下

(1)

(2)

式中:φjdSξ(i,j=x,y)为离散边界上单元的应力;Gij(x,ξ)和Tij(x,ξ)分别为位移和应力格林函数,表示单位力向量j作用在ξ引起x点i向的位移和应力。格林函数自动满足无限远辐射条件,同时满足波动方程。

2.2 边界条件及求解

需考虑的边界条件分为两类:①隧道外壁、基础外壁以及建筑底部的位移、应力连续性条件;②半空间地表、建筑物表面、隧道内壁的零应力条件。具体为:

(1) 自由水平地表边界L1上应力为零

(3)

(2) 基础底部边界界L2、L3、L4上位移和应力连续

(4a)

(4b)

(3) 剪力墙外表面边界L8、L9、L10上应力为零

(5)

(4) 剪力墙Ω1、Ω2、Ω3和基础T1、T2、T3的连接处L5、L6、L7上位移和应力连续

按照对比护理的方式进行研究，选取我院2017年1月～2018年8月所接诊病例76例，任选组中38例，以常规方式护理，即对照组，余下38例，则给与中西医护理干预，即观察组。对照组男20例，女18例，年龄34～57岁，平均（43.12±1.08）。而观察组则由男19例，女19例，年龄31～59岁，平均（45.82±1.45）。对以上各数据对比；差异无统计学意义（P＞0.05）。

(6a)

(6b)

(5) 隧道Ψ1、Ψ2衬砌外表面与半空间土体边界L11、L13上位移和应力连续

(7a)

(7b)

(6) 隧道域内壁L12、L14上应力为零

(8)

根据计算模型边界条件方程式(3)～式(8)和散射场位移应力表达式(1)～式(2),边界条件的积分表达式分别如下所示,并通过解以下边界积分方程求得虚拟波源密度,继而得到各分域散射场。由散射场和自由场叠加即得出总波场(衬砌与建筑物中仅考虑散射场),从而得到任意点的位移和应力。

(i,j=x,y)

(9)

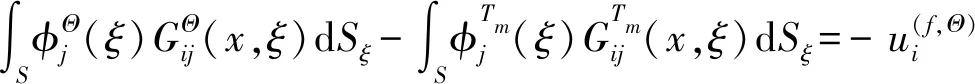
(i,j=x,y,m=1,2,3)

(10a)

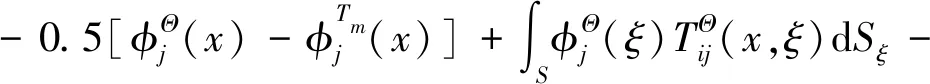
(i,j=x,y,m=1,2,3)

(10b)

(i,j=x,y,m=1,2,3)

(11)

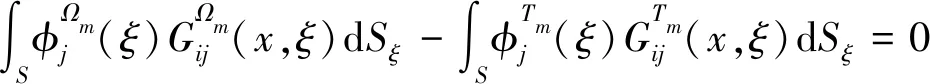
(i,j=x,y,m=1,2,3)

(12a)

(i,j=x,y,m=1,2,3)

(12b)

(13a)

(i,j=x,y,m=1,2)

(13b)

(i,j=x,y,m=1,2)

(14)

3 精度检验

为了检验方法精度,将本文模型退化为无建筑情况下地下圆形衬砌隧道对入射平面SV波散射的模型。验证中的参数取值为:黏滞阻尼比ζ=0.001,泊松比μ=0.25,无量纲频率η=0.25,隧道埋深取2倍的隧道半径。取半空间和衬砌材料的密度比ρ1/ρ2=1,剪切波速比β1/β2=1。图2为本文模型退化计算结果同边界积分方程法文献[9]的对比结果,横轴坐标对应地表面上各点点位x/a,纵轴坐标对应为地表位移幅值(地表位移幅值已由入射波的位移幅值标准化)。由图2可知,本文的方法同文献结果吻合良好,从而验证了本文方法的精确性。

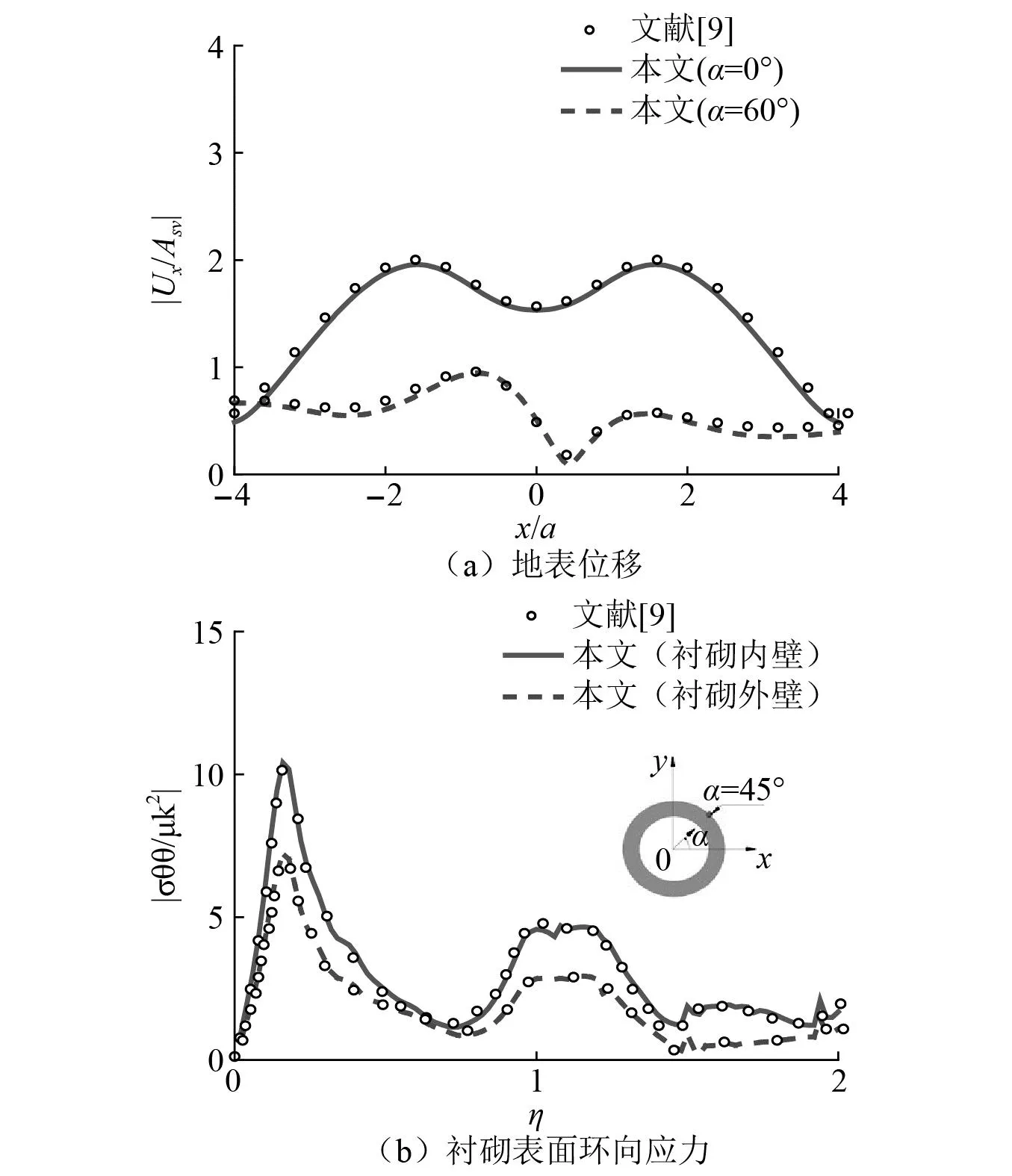
图2 本文退化计算结果与文献[9]的比较

4 算例分析

算例材料参数如表1所示,几何参数设置为:两隧道的外半径均为a1=4.4 m,内半径均为a=4 m;剪力墙的宽度高度和间距分别为B1=21 m、H=44 m和D1=40 m;三个基础的埋深均为h=4 m、宽均为B1=21 m。隧道埋深d=12 m,两隧道圆心之间距离为da=13 m。衬砌内外介质材料滞回阻尼系数均取0.05。地上建筑的基础部分假定为刚性基础,其剪切波速需要取充分大,经过我们前期对比分析发现其剪切波速取到10 500时便能满足各种情况下基础的刚性假设。其中剪力墙剪切波速在进行均匀化假设材料的等代弱化时,按照刚度等效原则进行换算,经过验证取为420 m/s。而在工程实际中场地土体等效剪切波速一般在200 m/s左右,因此我们以200 m/s进行计算。

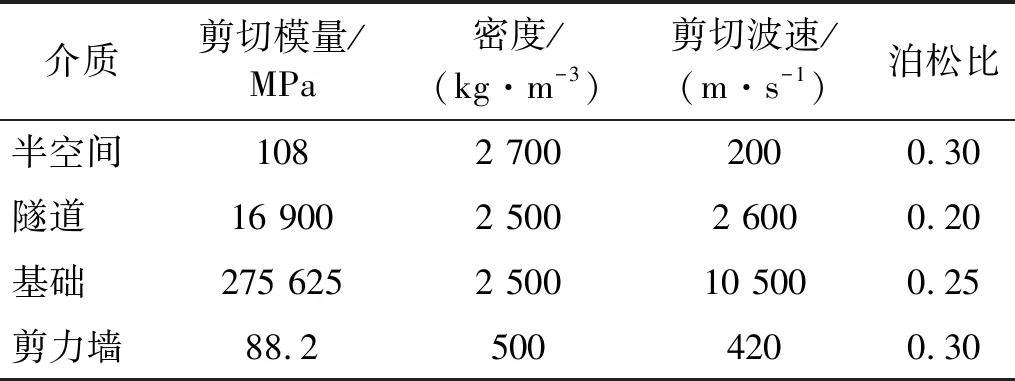
表1 材料参数

4.1 隧道群-建筑群体系对隧道地震响应的影响

图3给出了本文的四个计算工况。图4、图5分别给出了SV波垂直入射(α=0°)与近似水平入射(α=89°)时,图3(a)三建筑双隧模型、图3(b)单建筑双隧模型、图3(d)双隧道模型三种工况下的隧道环向应力分布云图。

图3 计算工况

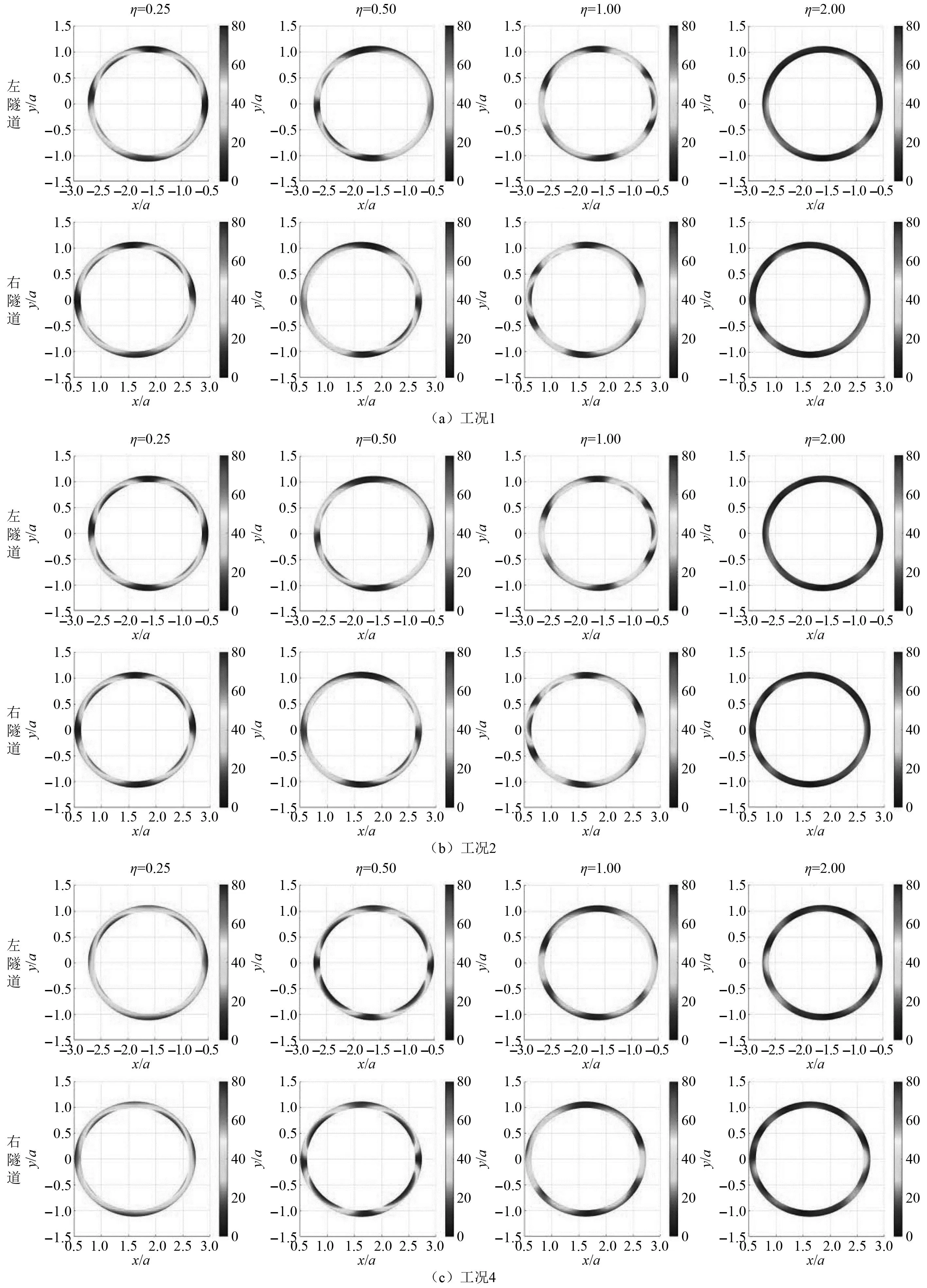
图4 SV波垂直入射时(α=0°)不同建筑物数量对隧道环向应力的影响

图5 SV波近似水平入射时(α=89°)不同建筑物数量对隧道环向应力的影响

当SV波垂直入射时(α=0°),工况1、工况2、工况4均为对称模型,因此左右隧道应力云图对称,故仅分析左侧隧道应力云图。由图4可知,三种工况下隧道应力幅值随着频率的升高有着相同的变化趋势,均会在某一频率后大幅度减小。当入射频率η由1增大到2时,工况1、工况2和工况4的应力幅值分别减小约63%、58%、20%。三种工况的应力分布情况也具有相同的变化趋势。当垂直入射波频率较低时(η=0.25),环向应力峰值出现在隧道上半拱左右两侧与竖向夹角约45°位置;当入射频率继续增加时(η=0.5),环向应力峰值出现在隧道上下半拱左右两侧与竖向夹角约45°位置。随着入射频率的不断提高,隧道内应力峰值分布情况更为复杂,出现了多个集中区域。

由图5可知,SV波近似水平入射的情况与垂直入射时相比,虽然三种工况隧道动应力集中现象更为显著,但水平入射情况下左隧道应力峰值仍远小于垂直入射时左隧道应力峰值。这说明入射角度的不同改变了体系的动力相互作用特性。

4.2 隧道群-建筑群体系对建筑地震响应的影响

本节研究了不同计算模型:工况1三建筑双隧模型、工况2单建筑双隧模型和工况3三建筑无隧道模型在平面SV波入射下的基础位移和剪力墙顶部相对位移。为了刻画剪力墙的刚度,定义无量纲参数ε=Hβ1/(2.625aβ4)。其中,2.625为基础长与隧道直径的比值,ε=0代表刚性的剪力墙,ε越大代表剪力墙刚度越小。SV波作用下剪力墙固有频率为

ωβ4=(2j-1)πβ4/2H(j=1,2,3)

(15)

当剪力墙结构ε=1(β4=840 m/s)时,无量纲固有频率ηβ4= 0.025、0.075、0.125…;ε=2(β4=420 m/s)时ηβ4=0.05、0.15、0.25…;ε=4(β4=210 m/s)时ηβ4=0.1、0.3、0.5…。

图6和图7分别给出了不同角度SV波入射时工况1、工况2和工况3中基础位移和剪力墙相对位移在频域中的图像。从图6、图7中可以看出,SV波入射时,基础水平位移值通常在剪力墙无量纲固有频率ηβ4处出现局部最小值。而剪力墙水平相对位移则在该频率附近存在局部最大值。

图7 不同入射角下剪力墙顶部相对位移响应频谱

对于平面SV波入射,基础动力响应与波的入射角度密切相关,这尤其体现在图6(b)工况1、工况3左侧基础的位移上。在SV波斜入射时,左侧基础的位移在高频情况下迅速增大,在SV波水平入射时达到最大,此时当η从1增大到2时基础水平位移增大了约13.4倍。入射角度的变化对剪力墙动力响应的影响则和基础类似。

观察图6(b)、图6(c)以及图7(b)、图7(c)可以发现隧道对较远建筑物的动力响应影响较小。工况1和工况3中两侧建筑物基础与剪力墙的各向位移差别不大,约在4%以下。而由图6(a)、图7(a)可知,两侧建筑物的存在会削弱中间建筑物基础与剪力墙的动力响应,且在SV波垂直入射时隧道的存在会对中间建筑物基础和剪力墙的动力响应产生屏蔽作用。当SV波以不同角度入射时,工况2基础与剪力墙各向位移峰值均大于其他两种工况;而当SV波垂直入射时,工况3基础与剪力墙各向位移峰值又大于工况1的位移峰值。

图8是SV波垂直入射时,剪力墙顶部相对位移随剪力墙刚度ε变化(取ε=0,1,2,4)的图像。当ε增大时,剪力墙水平位移和竖向位移峰值向低频移动,且最大峰值位移通常位于剪力墙自身固有频率的附近。这说明在整个体系中,剪力墙自身的特性在其位移过程中占主导地位。此外随着ε的增大,工况1和工况3两侧剪力墙的位移峰值呈现减小的趋势。这也是由于柔性结构具有更强地“吸收”地震作用的能力,产生较小的位移和应变。

图8 不同ε值下剪力墙顶部相对位移响应频谱

5 结 论

本文采用一种高精度间接边界元方法,对SV波作用下地上建筑群-地铁隧道群的动力相互作用问题进行研究。依托IBEM在求解复杂模型方面具有降低计算维度、计算效率高等显著优势,通过建立二维地上建筑群-地铁隧道群模型对该问题进行了系统的分析,研究结果表明:

(1) 入射波特性,隧道和建筑物的数量等因素是影响地上建筑群与地铁隧道群地震相互作用的关键因素。

(2) 在不同工况中,SV波垂直入射时隧道应力均远大于水平入射时,且垂直入射时近距离建筑物的存在使得隧道应力幅值波动较大,最大波动数值约为37.5%。

(3) 当SV波垂直入射时,ε=1时建筑顶部位移在第一、第三固有频率分别下降29.4%,66.7%,因此隧道会对其上方的建筑产生较大的屏蔽作用,并且对高频波的屏蔽作用更为明显。

(4) 建筑群的存在会使得单体建筑的动力响应减小。在波斜入射时,位移来波一侧的基础与剪力墙的位移会在高频波作用下会迅速增大,最多可增大13.4倍。建筑物刚度减小,则会使剪力墙位移峰值降低并向低频迁移,且峰值位移主要由剪力墙自身动力特性决定。

(5) 本文结果为于下穿隧道建筑物周围新建筑物时的动力响应提供了理论指导。

基于上述结论,笔者建议,在建筑群-地铁隧道群抗震设计中,应充分考虑其动力相互作用对其抗震性能的不利影响。