社区尺度斜入射波场下场地-建筑群耦合作用模拟方法

巴振宁, 付继赛, 王方博, 梁建文, 牛嘉琪

(1. 天津大学 建筑工程学院,天津 300354;2. 天津大学 滨海土木工程结构与安全教育部重点实验室,天津 300350;3. 天津大学 中国地震局地震工程综合模拟与城乡抗震韧性重点实验室,天津 300350)

土-结构相互作用(soil structure interaction,SSI)的存在会显著改变建筑周围的地震波场[1],进而导致临近建筑的响应产生彼此交互的影响[2]。已有研究证明,场地上存在多个建筑(2个及以上)时有必要考虑多建筑间的结构-土-结构相互作用(structure-soil-structure interaction,SSSI)[3-6]。近年来,随着世界经济的快速发展,城镇建筑愈发集中,尤其在城市区域已形成规模庞大的建筑群,地震波场在建筑(群)间反复反射,导致地震波场更为复杂,可能出现地震波幅值的异常放大和长周期地震动的形成等现象,且这一现象已于1985年墨西哥米却肯州地震震害调查中得到印证[7]。因此,为更准确地考虑地震波场分布及建筑反应,有必要对场地-城市相互作用(site-city interaction,SCI)进行系统的研究。

然而,由于涉及多尺度问题且计算量庞大,无法采用传统精细建模的方式对建筑进行模拟,因此如何对建筑进行简化并考虑建筑群与场地之间的耦合作用成为研究SCI效应的关键问题,现已有学者进行一些有益探索。

在二维方面,Wirgin等[8-9]将建筑简化为均匀弹性实体块,首次采用数值方法求解在SH波作用下二维理想建筑群-场地的耦合响应,在此基础上Kham等[10-13]采用二维边界元法研究了城市建筑群对场地地震动的影响;Gueguen等[14]将建筑物简化为三自由度弹性振子,利用格林函数将建筑基底反力施加在场地表面,并应用于墨西哥城罗马北区,但未考虑建筑与建筑之间的耦合影响;Boutin等[15]将建筑简化为单自由度振子,并进一步考虑了建筑之间的耦合;Ghergu等[16]将建筑和基础简化为由弹簧连接的两个集中质量点,将基底反力简化为均布荷载实现了建筑群与场地之间的耦合;刘铁林等[17-18]将建筑假定为集中质量简化模型,并基于被研究块体的概念,给出一种研究SCI效应影响的波动数值方法,实现了波场在建筑和场地之间的双向传播;Chen等[19]基于有限元方法实现了二维场地和线性多自由度(multi-degree of freedom,MDOF)建筑模型的耦合。

由于二维方法无法反映真实的建筑特性及分布情况,模型灵活性受限,且多数限于弹性和平面外(SH波)的情况,因此,亦有学者提出了用于模拟SCI效应的三维方法:Clouteau等[20-21]采用边界元法模拟了三维SCI效应;Fernández-Ares等[22-24]采用有限元方法模拟场地,并分别采用梁单元、实体单元和单质点振子(single degree of freedom,SDOF)模拟建筑反应;Sahar等[25-26]分别采用有限差分法(finite difference method,FDM)和谱元(spectral element,SE)法,将建筑假设为实体单元,建立了场地和建筑群耦合谱元模型。然而,以上方法大多采用实体块或单质点振子模拟建筑,且对建筑的模拟均处于弹性阶段,无法考虑建筑非线性和频谱特性。Lu等[27-28]采用谱元模型模拟场地,并采用由Lu等[29-30]发展的非线性MDOF模拟建筑,将建筑基底反力和荷载施加点的地表加速度作为交互对象,实现了基于SE方法和MDOF模型的耦合,该方法将SCI效应的研究扩展到了非线性,可较为真实地反映建筑非线性地震响应,然而,仅考虑了垂直入射剪切波(S波)作用下的结果,未能考虑入射角度和波型的影响。

上述现状表明,关于SCI效应的研究方法已取得一定发展,但目前仍处于探索阶段。本文发挥SE方法可快速高效求解三维地震波场传播和MDOF模型计算量小且可反映建筑非线性和频谱特性的优势,改进了SE模型与MDOF模型的耦合机制,同时,以频率波数域(frequency-wave number analysis,FK)方法求解斜入射波场,并结合FK-SE混合方法将波场输入,建立了FK-SE-MDOF耦合方法,实现了SE-MDOF耦合模型中多种波型的斜入射输入。

本文主要架构如下:首先,对SE-MDOF耦合方法原理进行介绍;然后,对FK-SE斜入射输入方法实现原理进行介绍;在验证方法正确性的基础上,以理想城市相互作用耦合模型为例进行计算分析,探讨了入射角度及波型对场地地震波场和建筑反应的影响。

1 SE-MDOF耦合方法

1.1 MDOF模型简介

MDOF模型将建筑每层的质量集中于一点,相邻两层之间采用弹簧阻尼器单元连接,如图1所示。考虑结构的非线性反应特性时,结构的动力平衡方程式为

图1 建筑MDOF简化模型

(1)

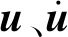
显然,层间恢复力模型是确定MDOF模型非线性反应的重要部分,目前学者大多采用三线性骨架模型对层间恢复力进行模拟,如图2所示。已有研究表明,该模拟方法计算结果与精细有限元模拟结果及试验结果吻合良好[31-32],因此,在现阶段计算机发展水平下,该方法为SCI效应研究中建筑群的动力时程分析提供了有效手段。本文层间恢复力模型参数的确定原则参考吴开来等研究中的方法。

图2 三线性骨架模型

1.2 SEM方法简介

SEM最早由Patera[33]应用于流体力学之中,20世纪末被应用于地震波场模拟领域,其求解弹性波传播问题的控制方程[34]如式(2)所示

(2)

式中:ρ为质量密度;s为位移;T为应力;f为体力; 下标t为时间; ∇为梯度算符; ∂为偏导算符。

SEM结合了有限元法建模灵活和谱方法精度高、收敛快的特性,阶数为4时每波长仅需1个网格即可达到较高精度,可极大降低计算存储和计算量。Komatitsch等基于SEM理论,采用Fortran语言开发了Specfem 3D软件,并获2003年Gordon Bel奖,该软件为开源软件,对相关学者进行二次开发等工作十分友好,现已被广泛应用。因此,本文选用该方法对场地地震波场进行模拟,并以Specfem 3D软件包为基础进行二次开发,实现场地与地表建筑的耦合。

1.3 SE-MDOF耦合方法原理

Lu等提出将本时刻求得的基底反力施加于下一时刻的场地表面,并基于开源SEM程序SPEED实现SE模型与MDOF模型的耦合计算。本文参考Lu等研究中场地-建筑群的耦合流程,进一步改进了耦合机理,避免了直接采用基底反力在场地加载点处的加速度数据与MDOF模型进行交互而可能存在的数值奇异问题,如图3所示,其具体步骤如下:

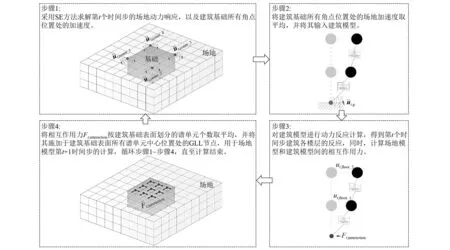
图3 SE-MDOF耦合方法流程

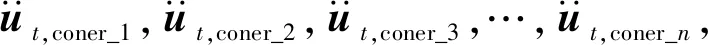
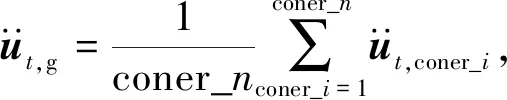
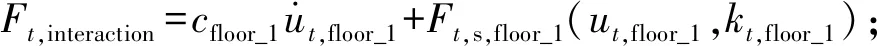
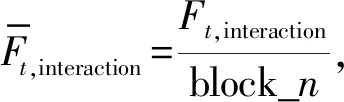
需要说明的是,本耦合流程对于建筑的模拟主要关注水平向破坏,暂未考虑竖向地震动对建筑的影响。

1.4 正确性验证

Schwan等[35]于2016年采用聚氨酯泡沫模拟场地,采用周期分布的通长铝板模拟上部结构,开展了场地-城市相互作用的缩尺振动台试验研究。本节采用SE-MDOF耦合方法建立Schwan振动台试验中2种布局(场地与1个和5个上部结构耦合)的数值模型,以检验该耦合方法的正确性。所建立的场地及上部结构模型如图4所示,其中场地尺寸为2.13 m×1.76 m×0.76 m,单元尺寸为0.07 m,P波波速vp=48.97 m/s,S波波速vS=33.50 m/s,密度ρ=49.00 kg/m3,场地阻尼比ξs=0.049;上部结构高18.70 cm,采用20个等间距集中质量点模拟上部结构,单个质点质量m0=13.30 g,一阶频率f1=8.45 Hz,上部结构阻尼比ξb=0.04;模型侧面以及顶面为自由边界,且顶面四周边线竖向固定;底面沿x方向输入加速度,y和z方向固定,加速度时程为主频8.00 Hz的Ricker波,峰值为0.26g。本方法与文献[35]Schwan振动台试验中建筑和场地反应的对比,如图5所示。对比结果表明,该方法与试验结果基本一致,验证了该SE-MDOF耦合方法在处理建筑-场地耦合及建筑群-场地耦合问题时的可靠性和正确性。

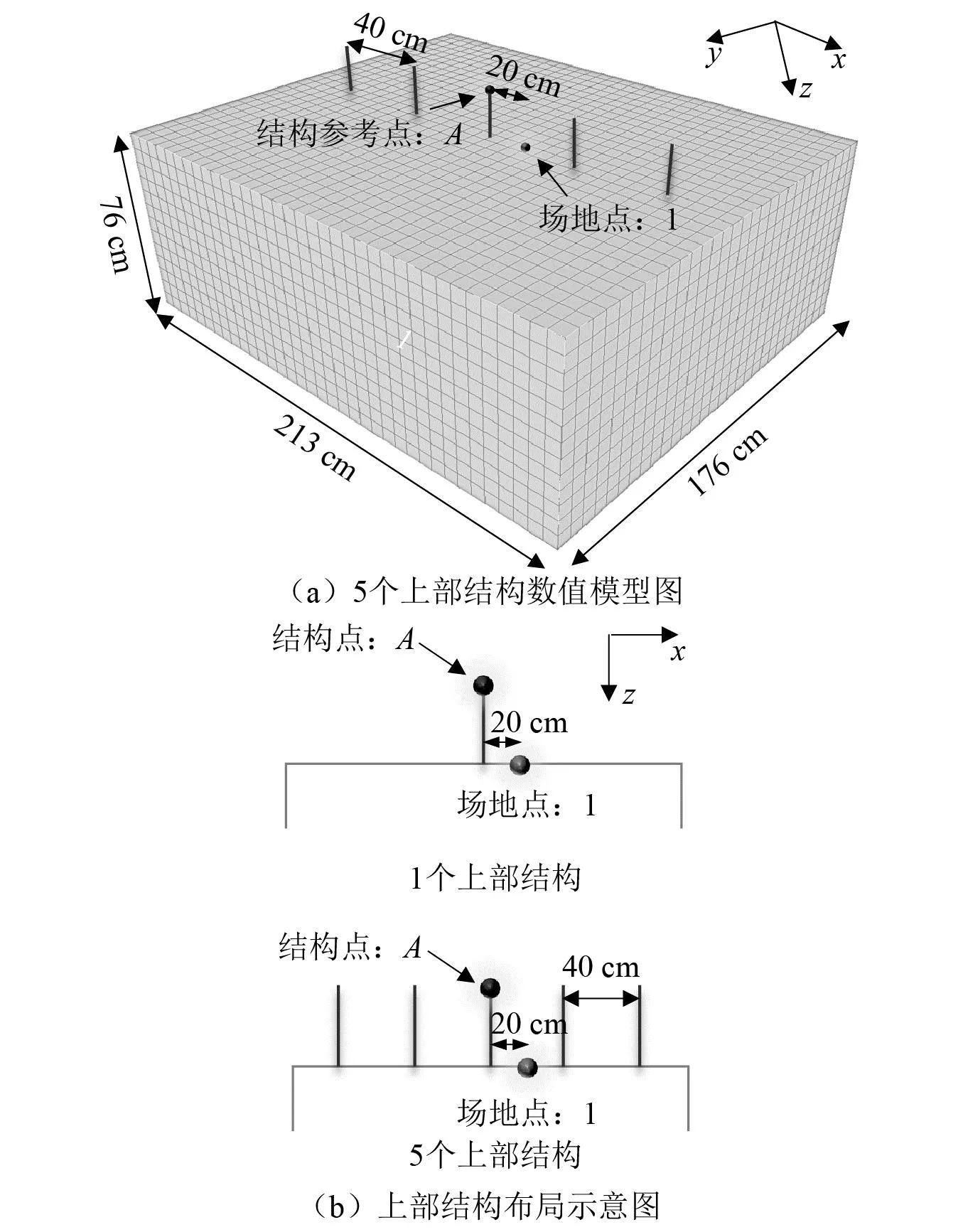
图4 振动台数值模型

图5 数值模拟与文献[35]中振动台试验中结果对比

2 场地地震波三维输入FK-SE混合方法

2.1 地震波场斜入射输入原理

斜入射的实现主要包括地震波场的输入和斜入射自由波场的计算,以下就本文中这两方面所采用的实现方法进行简要介绍。

在地震波场输入方面,刘晶波等[36]基于黏弹性人工边界提出了将地震波场转化为人工边界上的等效输入载荷的波动输入方法,并给出了一维模型等效荷载计算公式,如式(3)所示。该方法具有较高精度,近年来已被诸多学者采用[37],依据式(3)及黏弹性边界条件理论,进一步可推导三维模型等效荷载计算公式,如式(4)所示

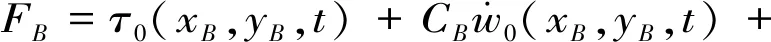
(3)

(4)

在自由波场计算方面,FK方法作为一种半解析方法,首先在频域中计算,然后利用傅里叶变换即可得到时域结果,具有无需划分网格、精度高、计算快的特点[39-40],因此,本文采用FK方法计算自由场。

在SE模型建立后,采用FK方法求得SE模型边界所有GLL节点位置处的位移、速度和应力后,由式(4)即可将地震波场转化为GLL节点处的等效输入载荷,进而实现斜入射情况下的场地-建筑群耦合模拟。

2.2 正确性验证

作者已将上述输入方法(下文简述FK-SE输入方法)开发至Specfem 3D程序,为检验其正确性,本节采用FK方法和FK-SE输入方法计算同一场地在斜入射地震波下的响应,场地参数如下:场地P波波速vp=3 000 m/s,S波波速vS=1 500 m/s,密度ρ=2 000 kg/m3,阻尼比ξ=0.005,SE场地尺寸为600 m×600 m×300 m;平面P波、SV波和SH波均以水平向夹角70°输入,输入地震波时程为主频2.0 Hz、位移峰值为1.0 m的Ricker波,如图6所示;对比点为地表点,坐标为(0,0,0)。分别采用FK和FK-SE输入方法得到的位移响应时程对比结果,显然两种方法完全吻合,验证了该方法及所编写程序的正确性,如图7所示。

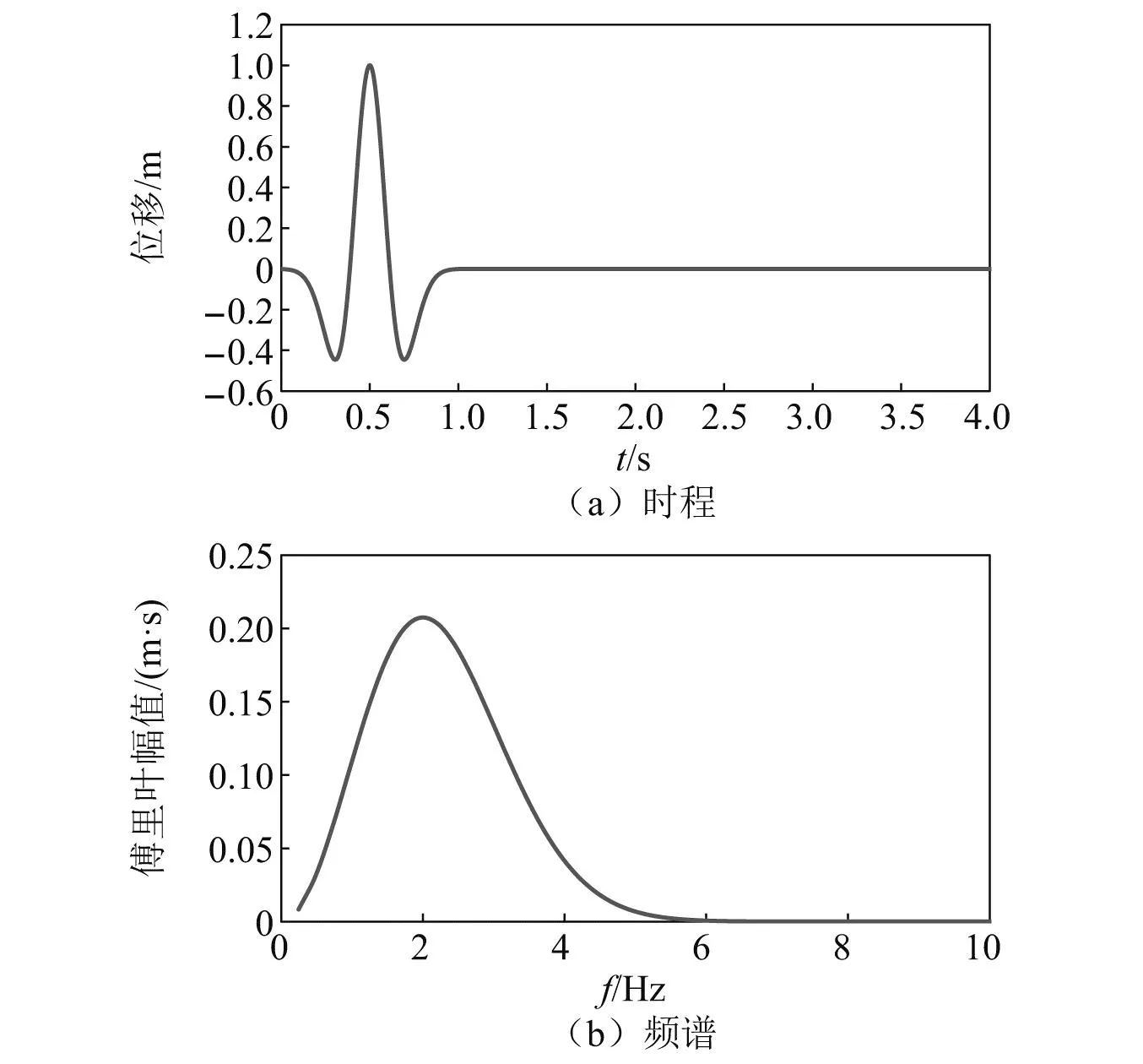
图6 FK-SE混合方法验证输入的Ricker波位移时程及频谱

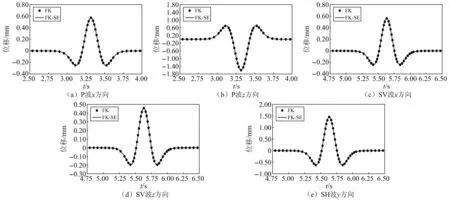
图7 FK-SE混合方法验证结果

3 算例分析

本章采用上述方法建立典型城市建筑群-场地耦合模型,检验了该方法对于社区尺度SCI效应问题研究的适用性,并进一步探讨了入射角度及波型对SCI效应的影响。

3.1 SV波垂直入射算例

对于社区尺度,建筑基础轮廓对地震波场分布及地震动特性存在不可忽视的影响,为检验本文所提出方法对于社区尺度SCI效应分析的适用性,本节以一典型9栋(3×3)建筑群为例进行计算展示,建筑平面布局示意图如图8所示。SE场地模型尺寸为800 m×800 m×100 m;基础尺寸为20 m×20 m×5 m,建筑层数为5层,层高3 m,建筑间净距20 m,根据经验公式取单位建筑面积质量为800 kg/m2,场地及基础材料参数如表1所示,根据GB 50011—2010《建筑结构抗震规范》[41]可知,该场地类别属于Ⅲ类场地,入射方向与水平面夹角为90°,输入波型为SV波,地震波时程选用加速度峰值为0.1g、主频为8.0 Hz的Ricker波,其时程及频谱如图9所示。

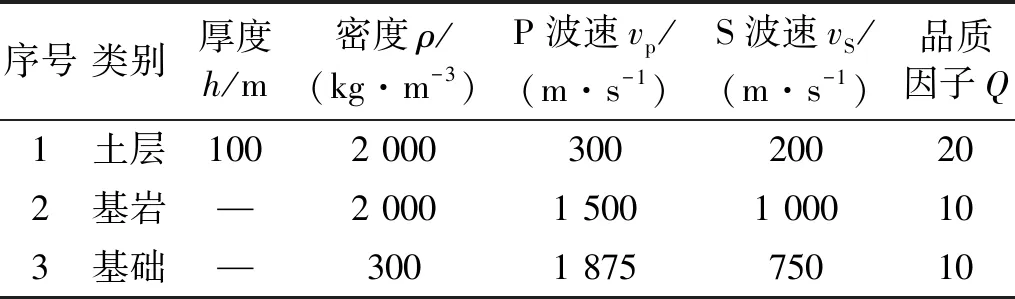
表1 算例材料参数

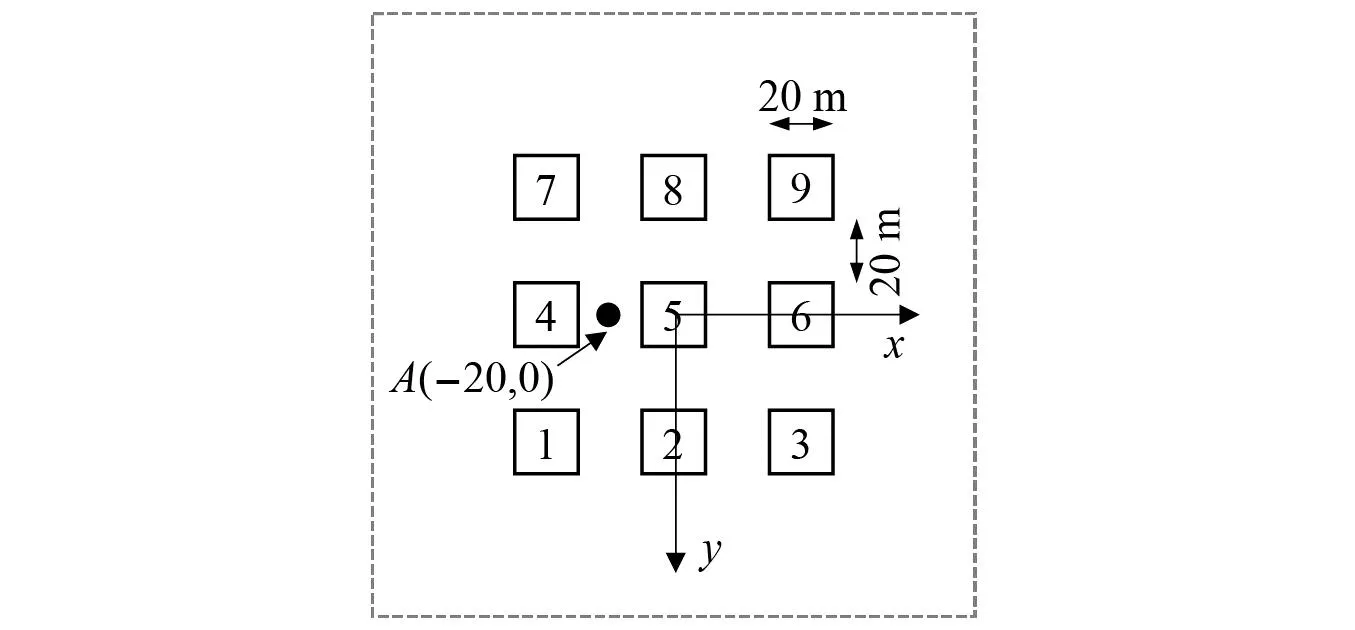
图8 建筑群平面布局示意图

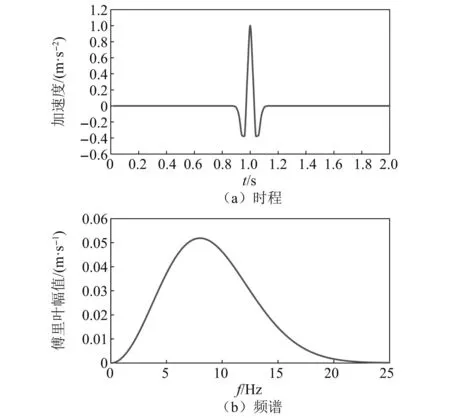
图9 主频8 Hz的Ricker波加速度时程及频谱

在场地方面,该耦合模型在SCI效应影响下场地地表加速度相对于自由场模型的变化率,如图10所示。场地A点处和5号建筑基础中心位置处加速度时程曲线,如图11所示。结合图10和11可知,建筑群的存在显著改变了地表的地震波场分布,具体表现为:在建筑与建筑之间的地表,场地加速度响应被明显放大,最大放大幅度达24%;在建筑基础内部,相对场地明显减小,最大减小幅度为30%;在建筑基础轮廓附近,加速度变化率不大;同时,由图10可知,单个建筑轮廓和建筑群整体对地震波场的辐射影响。另外,由图11可知,建筑群内地表地震动与自由场相比波动性显著加强,该现象应为地震波在建筑之间发生反射所导致。

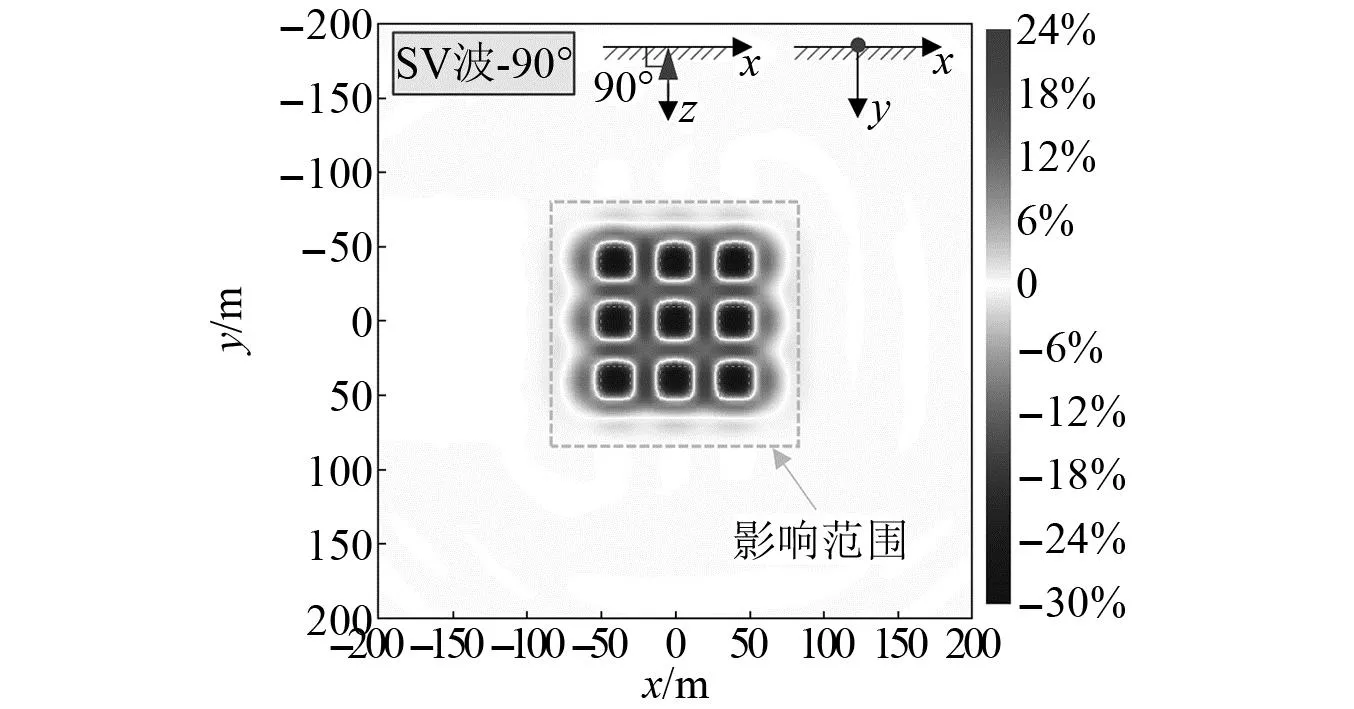
图10 垂直入射SV波作用下场地地表加速度峰值变化率

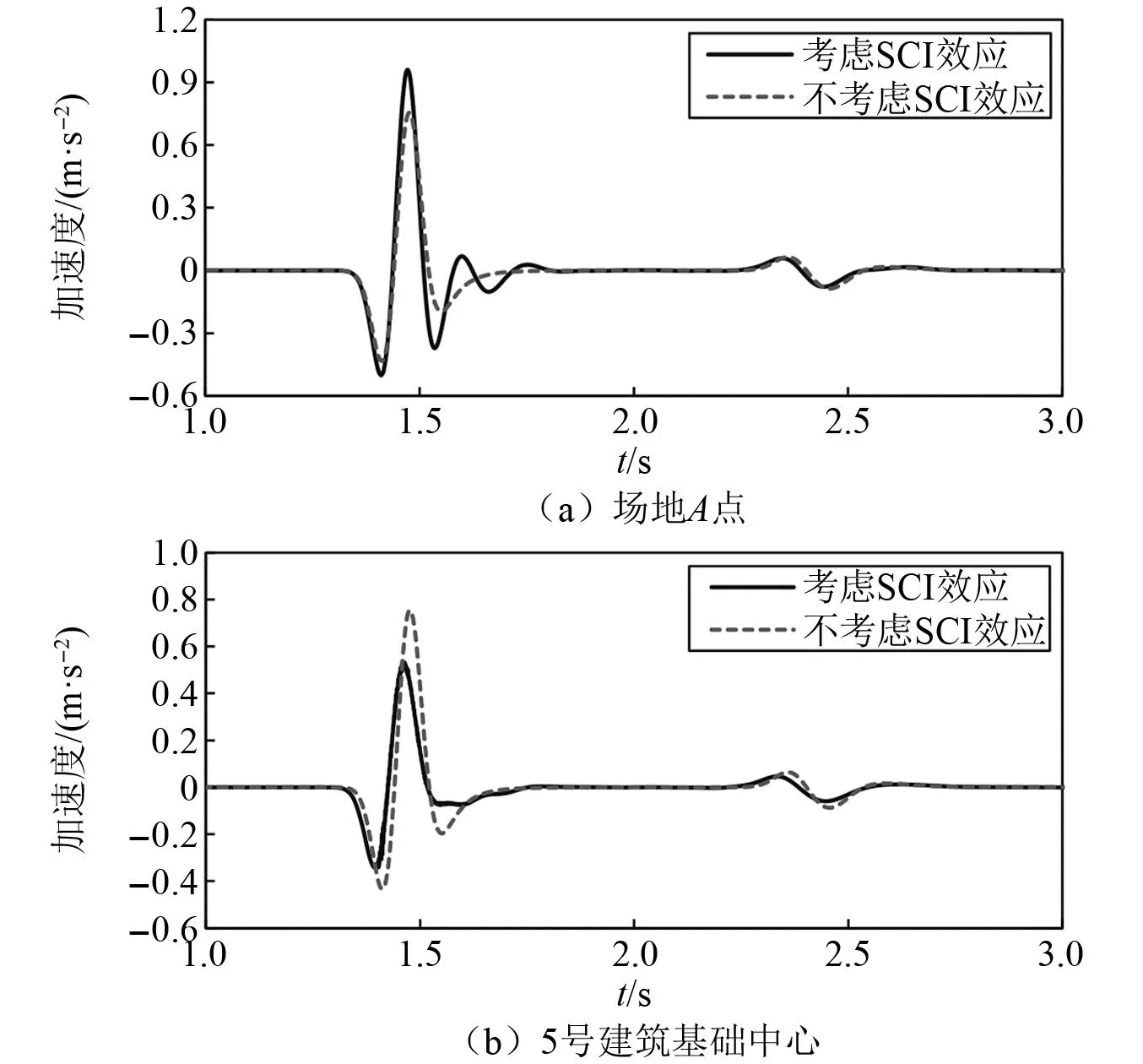
图11 垂直入射SV波作用下考虑和不考虑SCI效应下场地A点及5号建筑基础中心处加速度反应时程对比

在建筑反应方面,考虑和不考虑SCI效应情况下5号建筑底层位置处层间位移角时程对比(注:不考虑SCI效应即直接采用地表自由场地震动作为输入),如图12所示。考虑SCI效应影响下建筑最大层间位移角相对于不考虑SCI效应的变化率,如图13所示。由图12可知,考虑SCI效应后建筑层间位移角明显降低,本算例中降低幅度达18%,对建筑破坏呈有利影响;进一步结合图13可知,本算例中SCI效应对建筑群中不同位置处建筑的最大层间位移角反应的减弱效果差异不大,基本均处于18%左右。

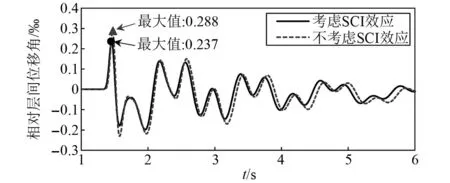
图12 垂直入射SV波作用下考虑和不考虑SCI效应5号建筑底层位置层间位移角时程对比

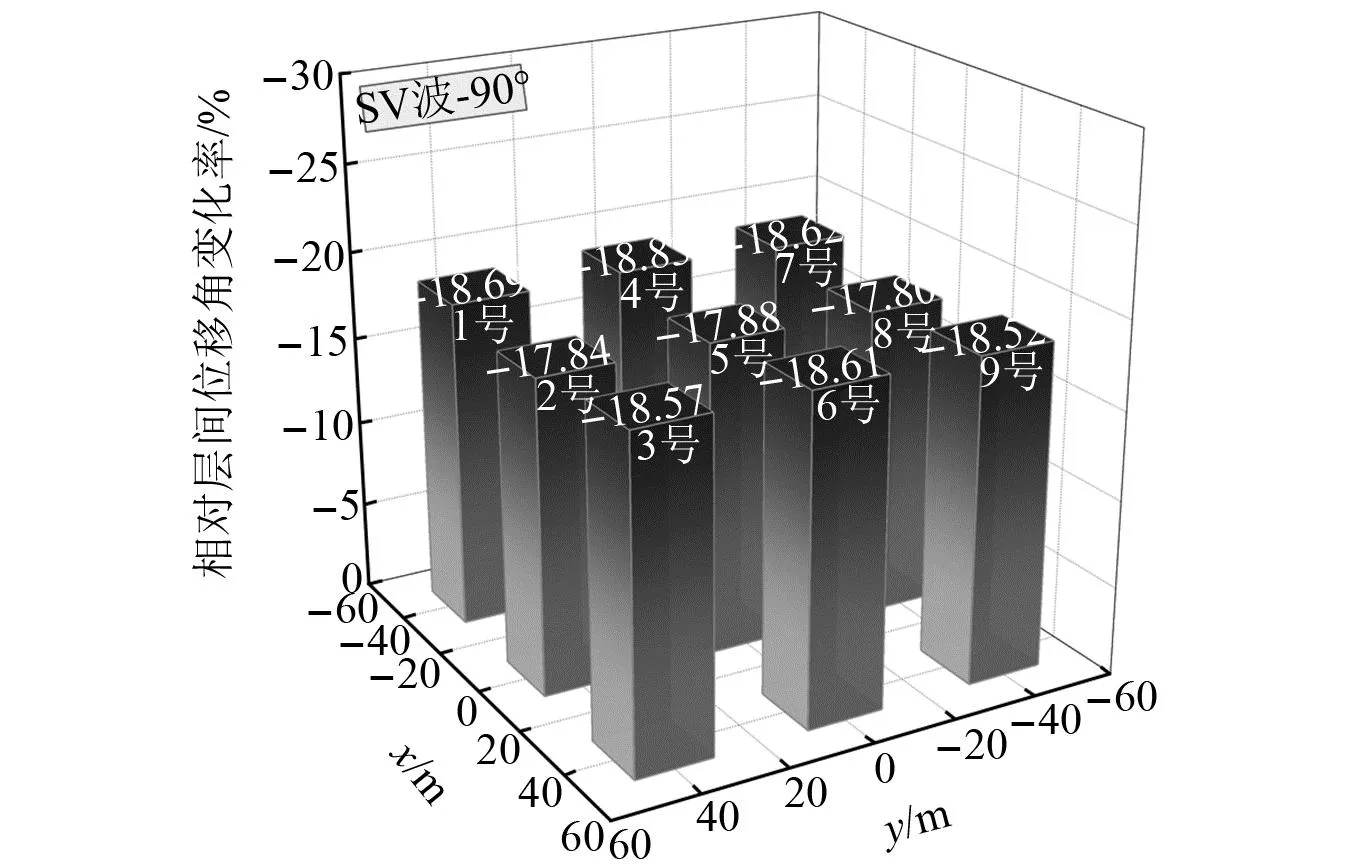
图13 垂直入射SV波作用下考虑与不考虑SCI效应建筑最大层间位移角变化率

以上现象与已有研究一致[42],再次检验了该计算方法的合理性,同时表明该方法可有效地反映建筑轮廓对临近地震波场及地震动特性的影响,可适用于社区尺度SCI效应的研究。

3.2 SV波斜入射算例

实际地震中,地震波场入射方向更多以斜入射为主,为进一步论证地震波入射角度对SCI效应的影响,本节以3.1节模型为基础,将入射波设为30°、45°和60°斜入射的SV波,并结合3.1节垂直入射情况进行对比。

在场地反应方面,SV波斜入射情况下场地-建筑群耦合模型在SCI效应影响下场地地表加速度相对于自由场模型的变化率,如图14所示。场地A点处加速度时程,如图15所示。结合图10、图14和图15可知,斜入射与垂直入射情况下,建筑基础内部加速度均被减小,但与垂直入射不同,斜入射情况下在场地上会同时存在加速度放大区和减小区;同时,在建筑群背波面一侧,建筑群对场地加速度分布的影响范围和程度要大于迎波面一侧,且伴随入射角度的减小,整体影响区域的范围逐渐变大,但值得注意的是建筑群对地表加速度峰值的影响程度并非随入射角度单调变化,其中本算例中45°入射下场地加速度峰值放大率最大,达80%。

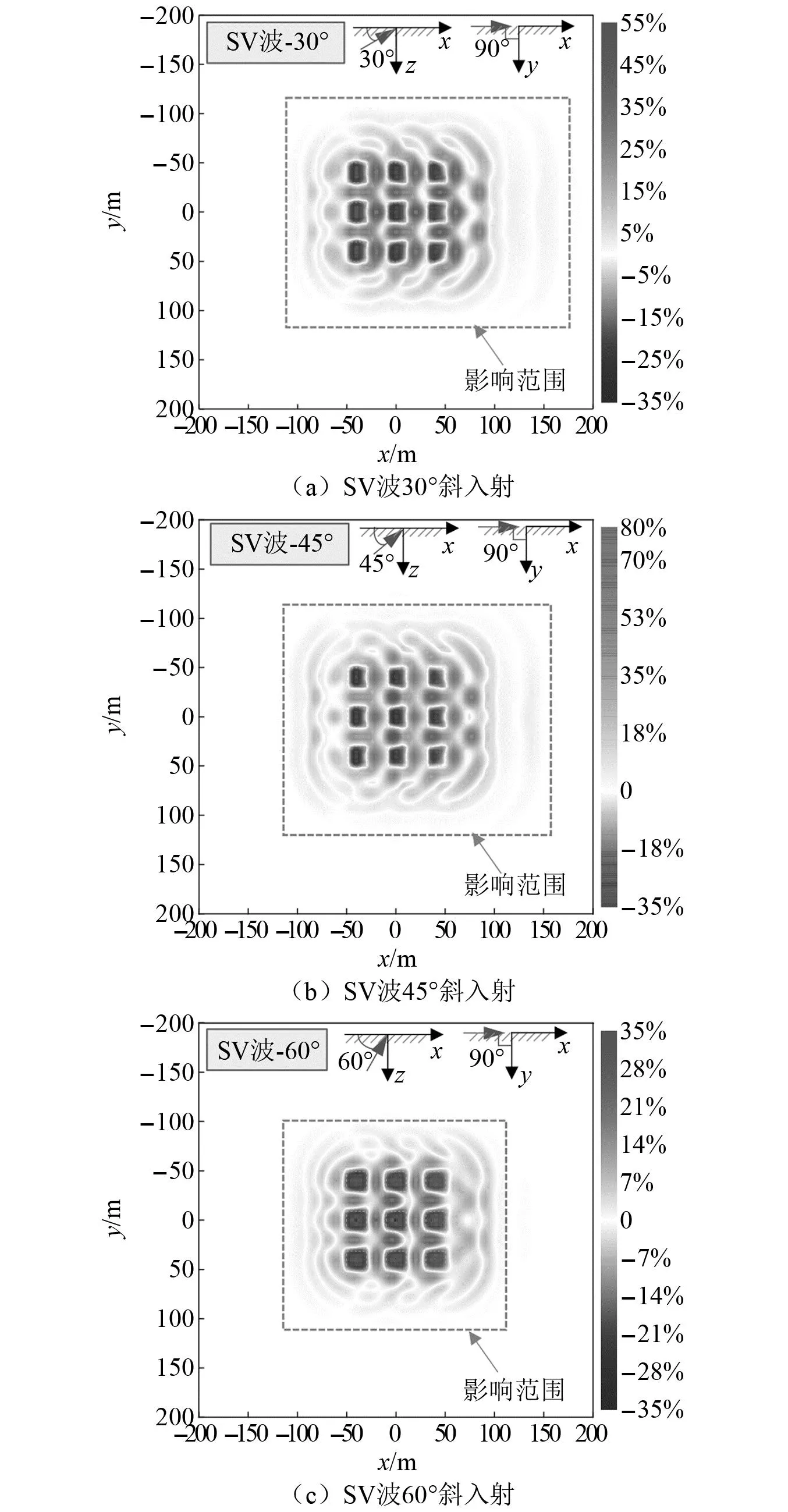
图14 斜入射SV波作用下场地地表加速度峰值变化率

图15 斜入射SV波作用下考虑与不考虑SCI效应场地A点处加速度时程对比

在建筑反应方面,该建筑群在斜入射和垂直入射SV波作用下最大层间位移角对比结果,如图16所示。考虑SCI效应影响下建筑最大层间位移角相对于不考虑SCI效应的变化率,如图17所示。结合图16和17可知,SV波斜入射情况下,建筑层间位移角响应明显小于垂直入射,但该减小效应并非随入射角减小而单调变化(例如:45°与30°入射下建筑最大层间位移角十分接近,且45°入射下2号、5号、8号建筑层间位移角略大于30°入射);另外,由图16可知,与垂直入射相比,斜入射情况下不同位置处的建筑最大相对层间位移角存在一定差异,且60°入射尤为明显;同时,由图17可知,斜入射情况下不同位置处建筑最大层间位移角变化率也明显不同,大体表现为迎波面变化率大于背波面,其中45°入射下5号与7号建筑最大层间位移角变化率差异达13.24%。

图16 斜入射及垂直入射SV波作用下建筑相对层间位移角对比

图17 斜入射SV波作用下考虑与不考虑SCI效应建筑最大层间位移角变化率

另外,为进一步观察斜入射波场传播过程中SCI效应的影响过程,SV波垂直入射和60°斜入射下典型时刻该场地-建筑群耦合模型变形云图,如图18、图19所示。

图18 SV波垂直入射典型时刻建筑群-场地耦合模型位移云图

图19 SV波60°斜入射典型时刻建筑群-场地耦合模型位移云图

由图18可知,垂直入射情况下,地表建筑运动完全同步;而由图19可知,在斜入射情况下,建筑群对地震波场的散射影响以及同一时刻不同位置处建筑的响应差异(1.40 s尤为明显),其差异原因应为垂直入射下地震波同时到达地表各点,而斜入射地表地震波场到时有所差异。该现象进一步有效展示了斜入射地震波场在传播过程中由传播路径和耦合作用影响所导致的波场及建筑响应的时空差异。

整体上看,与垂直入射相比,斜入射SV波情况下建筑群对临近场地地表加速度峰值分布的影响更为剧烈、地表波场分布的时空差异更为复杂,建筑层间位移角响应则有所减弱,但不同位置处建筑响应的差异有所增加,尤其对于斜入射SV波下应更加关注位于背波面位置和中心位置处建筑的破坏。因此,在SCI效应研究中应重视斜入射的影响。

3.3 P波斜入射算例

实际地震波场包含多种波型,而以往研究多以S波入射为主,为探讨波型对SCI效应的影响,本节将入射波设为30°、45°和60°的P波(模型其余参数同3.1节),与3.2节SV波入射结果进行对比。

在场地反应方面,斜入射情况下建筑群-场地耦合模型在SCI效应影响下场地地表加速度相对于自由场模型的变化率,如图20所示。结合图14和图20可知,同一入射角度下,P波与SV波入射下建筑群对地震波场分布的影响明显不同,甚至存在在同一位置处SV波入射下场地加速度为放大区域而P波入射下为减小区域的现象(例如:60°入射下5号与8号建筑之间的场地);另外,与SV波不同,不同入射角度下SCI效应对场地地表加速度的影响范围差别不大,且呈现伴随入射角度的减小,影响程度逐渐减小的趋势。

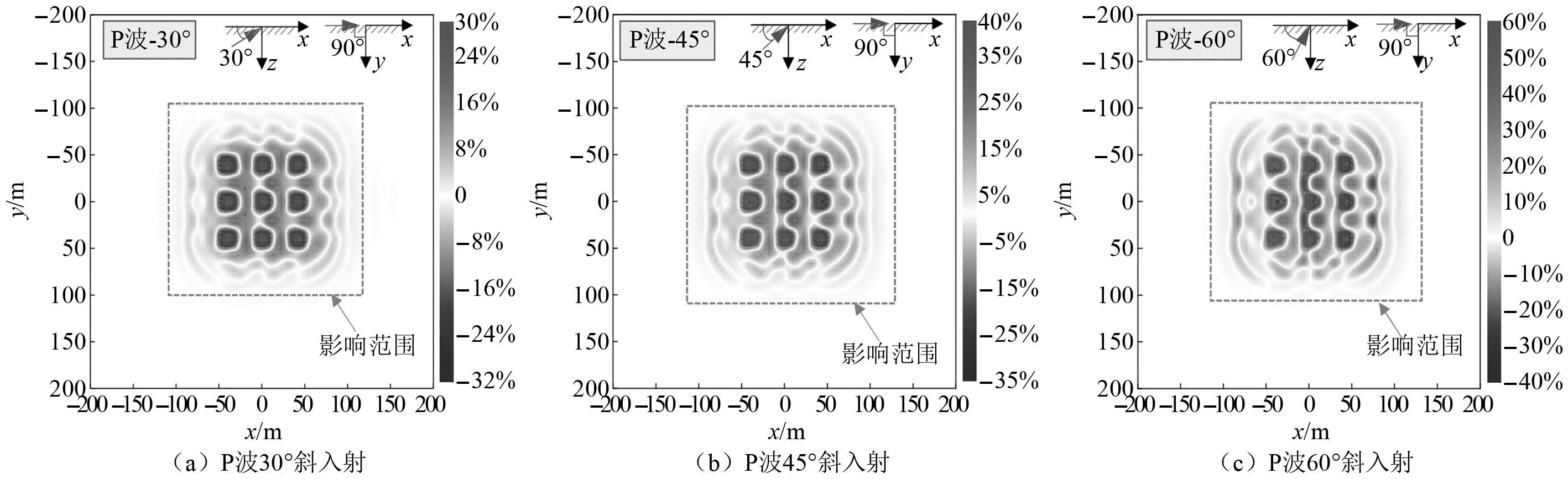
图20 斜入射P波作用下场地地表加速度峰值变化率

在建筑反应方面,该建筑群在斜入射P波作用下最大层间位移角对比结果,如图21所示。考虑SCI效应影响下建筑最大层间位移角相对于不考虑SCI效应的变化率,如图22所示。结合图21和图22可知,与SV波入射情况不同,随着P波入射角度的减小,最大层间位移角逐渐变大,且不同位置处的建筑层间位移角变化率差异不大。

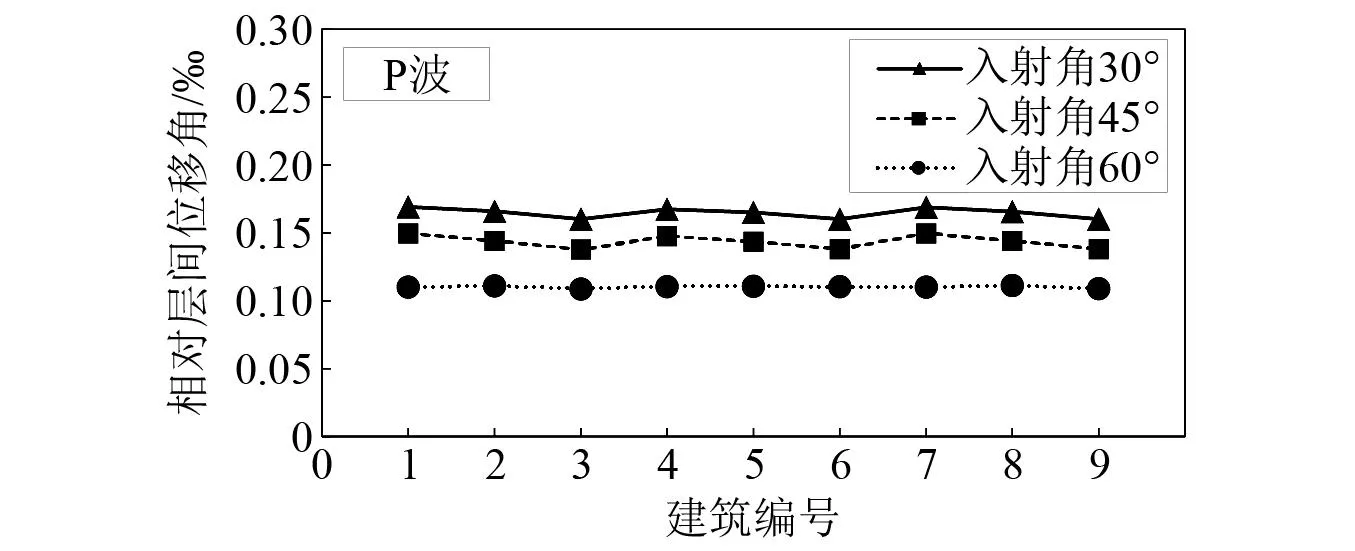
图21 斜入射P波作用下建筑相对层间位移角对比

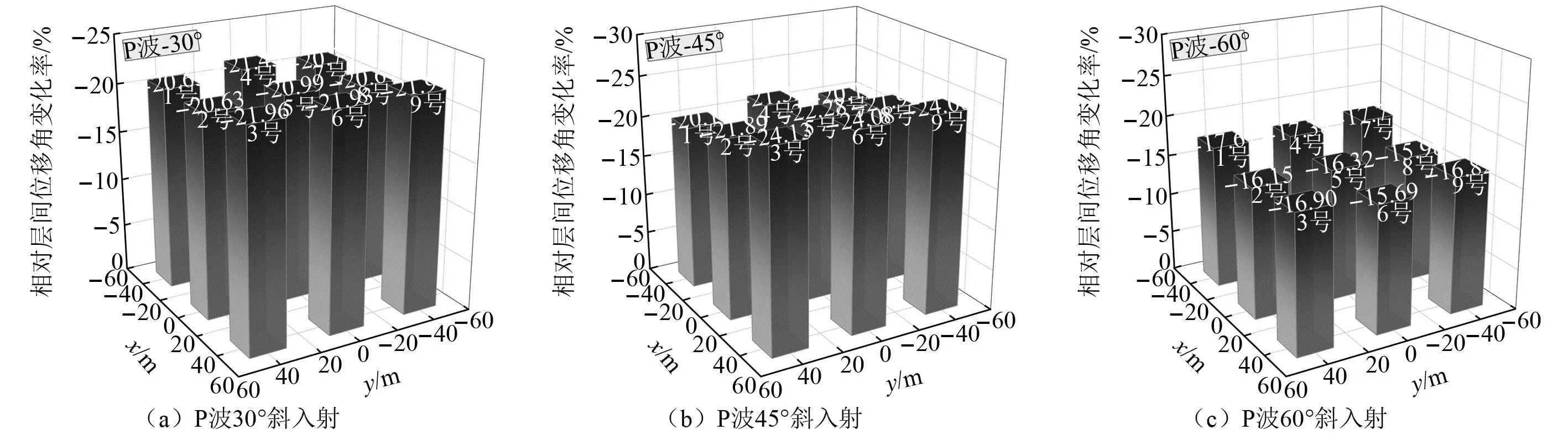
图22 斜入射P波作用下考虑与不考虑SCI效应建筑最大层间位移角变化率

总体上看,与SV波相比,P波入射下,建筑群对地震波场分布的影响明显不同,甚至在场地某些位置存在完全相反的变化规律;同时,入射角度对场地地表加速度峰值变化率范围、建筑层间位移角的影响规律均较为单一。因此,在SCI效应研究中应综合考虑P波和S波的影响。

4 结 论

本文提出了适用于社区尺度SCI效应分析的SE-MDOF耦合方法,并结合FK方法实现了多种波型的斜入射输入,在验证方法正确性的基础上,建立理想场地-城市相互作用耦合模型,论证了该方法的适用性,并探讨了地震波场入射方向和波型对SCI效应的影响,得到以下结论:

(1) 与垂直入射相比,斜入射情况下建筑群对临近场地地表加速度峰值分布的影响及建筑响应明显不同,建筑群响应存在明显时空差异,因此,在SCI效应研究中应重视斜入射的影响。

(2) 不同波型作用下,建筑群对地震波场分布的影响存在明显差异,甚至在场地某些位置存在完全相反的影响规律,因此,在SCI效应研究中应综合考虑P波和S波的影响。

(3) 斜入射下应关注不同位置处建筑响应的差异,尤其对于斜入射SV波入射下应关注位于背波面位置和中心位置处的建筑。

(4) 该方法有效解决了当前三维SCI效应模拟方法中未能同时考虑建筑非线性、频谱特性、地震波波型及入射角度等因素影响的问题,适用于需考虑基础轮廓信息的足尺社区尺度SCI效应研究,可为城市规划、抗震设计、风险评估以及震后救援等工作提供定量参考,对于韧性城市的建设具有重要意义。