少量样本下基于PCA-BNs的多故障诊断
王进花, 马雪花, 岳亮辉, 安永胜, 曹 洁
(1. 兰州理工大学 电气工程与信息工程学院,兰州 730050; 2. 甘肃工业过程先进控制重点实验室,兰州 730050;3.兰州理工大学 电气与控制工程国家实验教学中心,兰州 730050; 4.甘肃华成建筑安装工程有限责任公司,兰州 730070)
近年来,越来越多的故障诊断方法被提出[1-7],特别是基于深度学习的智能故障诊断方法被研究者广泛应用于各种各样的机械设备故障诊断。Wang等[8]针对滚动轴承的自动特征提取和故障识别问题, 提出了一种基于多头注意和卷积神经网络的数据驱动智能故障诊断方法。Chu[9]等提出了一种基于多膨胀率和多注意机制的机械故障多尺度卷积模型(MDRMA-MSCM)。Zhu等[10]提出了一种对称点模式,将转子振动信号转换成二维图像,然后利用这些图像训练卷积网络进行故障诊断。Khan等[11]以电机电流为输入,结合一维CNN和LSTM网络,建立了匝间故障诊断的解析模型。
深度学习的方法由于其强大的非线性特征自适应提取能力和表征能力而受到故障诊断等领域的广泛重视[12-13]。然而,基于深度学习的故障诊断方法需要通过大量的有标签数据进行训练,才能达到较高准确率。例如工作环境在偏远的海上或者山区的设备,很难获取到有标签故障的样本数据,以及诊断对象知识的不精确,使得故障诊断过程中往往不确定性问题占据多数,使得大多故障诊断技术越来越难以满足可靠性要求。在工程领域中,监测数据大多为正常数据仅有少量故障样本数据,在少量样本下的故障诊断已成为故障诊断领域的研究热点[14]。
少量样本问题的实质是信息不足,建模方法的有效性体现在对少量样本数据潜在信息的充分挖掘。一般而言,数据信息挖掘越充分,建立的分类器的分类性能就越好。因此,选择一个在故障标签样本数据少的情况下,能达到高诊断率的方法非常重要。而贝叶斯网络可以将样本数据集以条件概率的形式表示,充分挖掘到数据信息。还可以通过因果关系的发现来构建科学、可靠和易于理解的网络模型,特别是在处理少量样本数据和不确定性知识方面,显示出其独特的优越性[15]。
文献[16]介绍了一种基于贝叶斯网络的核电厂多源传感器节点故障诊断框架,该框架具有易于可视化、参数不确定性表达、能够在数据不完整情况下进行诊断等优点。文献[17]提出了一种改进的贝叶斯网络(Bayesian network,BN)用于故障诊断,在田纳西-伊斯曼过程(Tennessee-Eastman process,TEP)上验证了该方法的有效性。文献[18]提出了一种基于贝叶斯网络的故障隔离方法。使用状态变量或贝叶斯网络中的节点来参数化各种故障和症状。文献[19]提出了一种基于贝叶斯网络的智能故障诊断网络,对某变冷流量空调系统进行了评价,验证了该策略的有效性和高效性。文献[20]提出了一种基于期望最大化算法(expectation maximization algorithm,EM)和贝叶斯网络的FD方法,解决建筑能源系统在数据缺失情况下的故障检测问题。
虽然贝叶斯网络因为它的各种优势,在故障诊断领域得到了大力的发展。但是,通常用贝叶斯网络进行故障诊断,首先需要对数据进行处理,得到离散化特征,然后用各种算法去学习特征与故障类别间的结构关系,使得整个方法的时间大大增加,相对于深度学习等故障诊断方法,用时更长。为了克服这一问题,本文提出了一种融合单故障贝叶斯网络构建多故障贝叶斯网络结构的方法。首先采用主成分分析(principal component analysis,PCA)来对故障数据进行处理。PCA是一种广泛应用于高维数据分析的统计工具,通过降低原始数据集的维数来总结特征[21-23]。采用PCA来对单故障数据进行降维,得到与数据相关性最大的一些故障特征,因为通过PCA降维后得到的特征是相互独立的,另外,得到的这些特征都是与原始数据相关性最大的,因此可以认为每个特征对该故障都是有影响的,这样可以直接得到单故障贝叶斯网络。然后融合单故障贝叶斯网络,得到多故障贝叶斯网络结构。这种贝叶斯网络构建方法不需要用额外的算法学习贝叶斯网络的结构,缩短了诊断时间。另一个限制贝叶斯网络应用的重要原因是,大多文献里在进行网络模型构建时,需要多个传感器的信息或者多个设备部位的信息[24-27],对于数据难以获取的设备,应用受到了很大的限制。
基于以上分析,本文提出一种基于PCA-BNs的故障诊断方法。该方法只通过一个传感器采集到的一维时序信号就可以进行贝叶斯网络的建模,克服数据不足情况下的建模问题。通过PCA对一维时序信号降维,得到与原始信号相关性最大的一些特征,直接构建单故障贝叶斯网络,然后融合单故障贝叶斯网络构建多故障贝叶斯网络结构,减少BN建模过程的时间;为了得到精确的网络参数,通过极大似然估计得到先验概率,用高斯分布和极大似然估计结合的方法得到条件概率;通过对电流信号和振动信号分别在少量数据下进行故障诊断,得到了良好的诊断效果。
1 贝叶斯网络
1.1 贝叶斯分类
在故障分类任务中,令父节点C为目标类别节点,包含r个系统故障类型c1,c2…cn;子节点x1,x2…xn代表n个故障特征[28]。故障诊断模型在故障发生后,需对未知类别的故障数据进行故障类型的判别。基于贝叶斯的故障诊断模型,通过对历史故障数据学习得到的故障信息,对未知类别的故障数据进行预测。其故障分类原理是基于贝叶斯公式推理得出的,具体过程为
当观测信号x={x1,x2…xn}进入诊断系统,n是故障特征个数,根据贝叶斯公式可求得其后验概率如式(1)所示
(1)
当边缘概率P(x)对所有故障类别是相同时,式(1)可简化为式(2)
P(C=ci|x)∝P(x|C=ci)P(C=ci)
(2)
假定在目标类别的条件下子节点间是相互独立的,其联合概率分布的计算可进一步简化为各个子节点乘积的形式,如式(3)所示
(3)
将式(3)代入式(2)中可得分类器的目标函数如式(4)所示
(4)
由目标函数可得,贝叶斯分类器将故障数据归属于最大后验概率的对应类别。在训练过程中,只需对历史数据的学习,计算各个子节点在相应类别条件下出现的概率P(xj|C=ci)和类别变量的先验概率P(C=ci),即可进行后续分类。
1.2 主成分分析技术特征提取
主成分分析技术(principal component analysis,PCA) 是一种常见的数据分析方式,常用于高维数据的降维,可用于提取数据的主要特征分量。设有m条n维数据,PCA的算法步骤为:
步骤1将原始数据按列组成n行m列矩阵X;
步骤2将X的每一行进行零均值化,即减去这一行的均值;
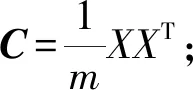
步骤4求出协方差矩阵的特征值及对应的特征向量;
步骤5将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P;
步骤6Y=PX即为降维到k维后的数据。
构建贝叶斯网络,一般都需要离散的特征节点。因此对一维时序信号进行贝叶斯网络建模,首先要对信号进行离散化,提取相应的故障特征。而使用小波变化等常用方法对一维时序信号进行提取特征,离散化后的特征失去了大量的信息,往往导致最后诊断率不高。而PCA在对信号降维后,得到的是与原始信号相关性最大的离散化特征,并且这些特征间相互独立,因此保留了大量的信息,可以克服对一维时序信号进行离散化提取特征后,丢失大量信息的问题。
1.3 改进多故障BN网络构建
从本质意义上讲,贝叶斯网络是一种有向无循环网络,其整体结构是由一个有向无循环图和若干条件概率表构成。它的网络结构由若干个节点构成,每一个节点对应一个变量,节点间相互依赖关系用有向无循环图进行表示,条件概率表用于描述节点依赖关系。在故障诊断领域,网络节点一般包括特征节点和故障类型节点,根据特征节点的状态和条件概率去计算每个类型节点的概率,最后选择概率最大的类型节点为发生的故障。
目前研究者们在进行网络模型构建时,特征节点往往需要多个传感器的信息或者多个设备部位的信息去构建,对于数据难以获取的设备,应用受到了很大的限制。因此,本文提出一种通过一个传感器信号就可以构建贝叶斯网络的方法,去克服此问题。本文构建网络方法的主要思想是首先对单传感器采集的单故障信号进行特征提取,构建单故障的BN结构,然后对单故障BN进行融合构成多故障BN。主要步骤为:
步骤1单故障BN构建
用PCA分别提取每种故障数据的n个特征。由PCA提取特征的特性,可知单故障的每个特征对其都有影响。因此直接可以进行单故障BN结构的构建,如图1所示,其中Fi为特征,Y为故障类别。

图1 单故障BN结构图
步骤2融合BN
每个单故障BN中的特征节点都是由PCA特征提取方法得到的,并且这些特征间相互独立以及与故障数据相关性最大,因此每个特征节点对每个故障类别节点都有影响。在融合两个单故障BN时,特征节点层不变,故障类别节点变为2个,并且每个特征节点与每个故障类别节点间均有关系。当进行一个二故障诊断时,将两个单故障BN融合,可以得到如图2所示的BN结构。
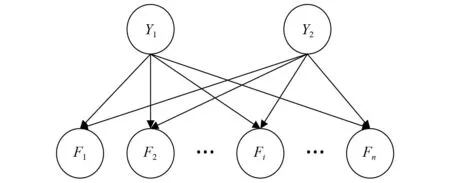
图2 二故障融合BN结构图
以此类推可以得到多故障BN结构图,如图3所示。
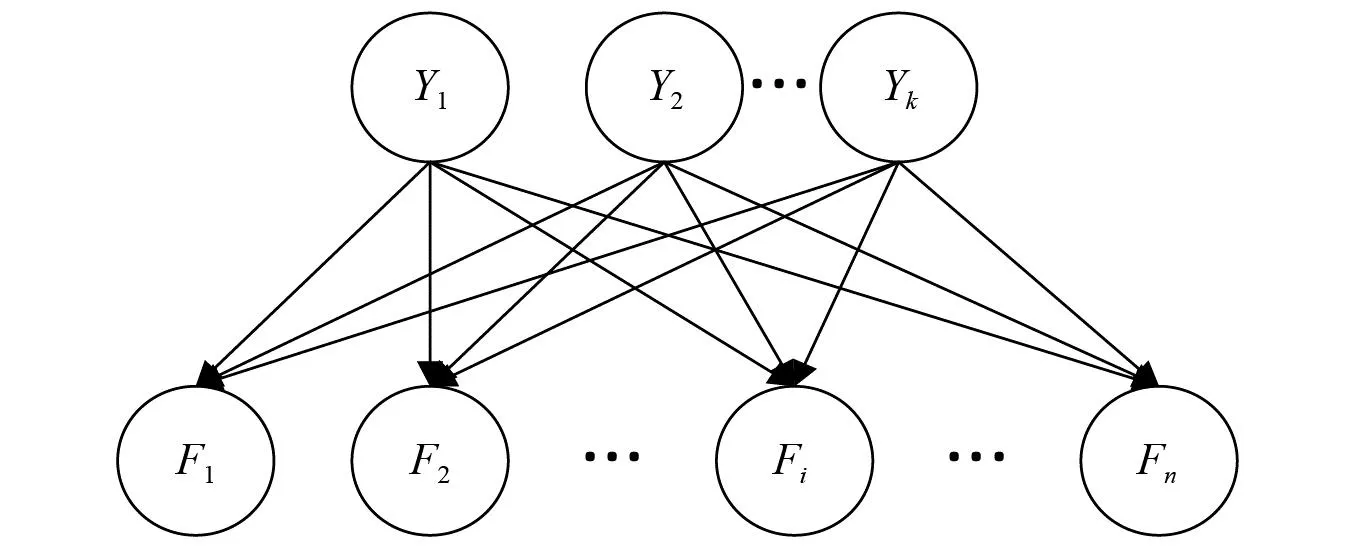
图3 多故障融合BN结构图
这种方法的优势是无需额外的算法去学习节点间的关系,进行网络结构构建,缩短了整个诊断方法的时间。另一个优势是该方法在构建BN时,只需要一个传感器的数据即可,应用范围更广泛,为数据难以获取的设备,提供了一种方法。
2 PCA-BNSs模型的构建
2.1 网络结构
本文试验数据是一维时序信号,把信号划分为2 000个采样点为一个样本。对单故障样本进行PCA降维,得到与信号相关性最大的一些特征。因为得到的特征之间相互独立,并且每个特征对类别都有影响,因此以特征作为节点可以直接得到两层的单故障BN结构。然后融合单故障BN得到最终网络结构。网络构建过程如图4所示,最终的贝叶斯网络,其每个特征对类别都有影响,也就是每个特征和类别间都有一个条件概率。

图4 贝叶斯网络模型
2.2 网络参数
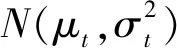
(5)

(6)
此时,当观测信号x={x1,x2…xd}进入诊断系统时,其后验概率如式(7)
∝P(Y=k)P(X=x|Y=k)=
(7)
用贝叶斯网络进行故障诊断的核心是求观测信号x={x1,x2…xd}进入诊断系统时,每个故障类别发生的概率大小。而由式(7)可以看出,实现此目标最重要的是求先验概率P(Y=k)以及μi,k、σi,k这两个参数。
使用极大似然估计去得到先验概率和μi,k、σi,k这两个参数,先验概率P(Y=k)的极大似然估计如式(8)所示
(8)
式中,I(a)是一个指示函数,如果a为真,I(a)结果为1,如果a为假,I(a)=0。用数学语言描述来说,P(Y=k)这个概率等于在N个样本的数据集中,类别为k的样本所占的比例。

所有参数估计完成之后,就可以计算给定样本的条件概率P(X=x|Y=k)以及先验概率P(Y=k)。进而通过公式P(Y=k)P(X=x|Y=k)得到每个类别的后验概率。具体计算如式(9)所示。
(9)
得到最大的P(Y=k|X=x),类别k即为模型分类的结果。贝叶斯网络可以将样本信息以条件概率的形式表示,在数据量较少时,能充分挖掘到数据信息,因此能够提高少量样本情况下的诊断准确性。
2.3 PCA-BNs的故障诊断
本文提出了一种针对一维时序信号构建贝叶斯网络,进行故障诊断的方法,流程图如图5所示。
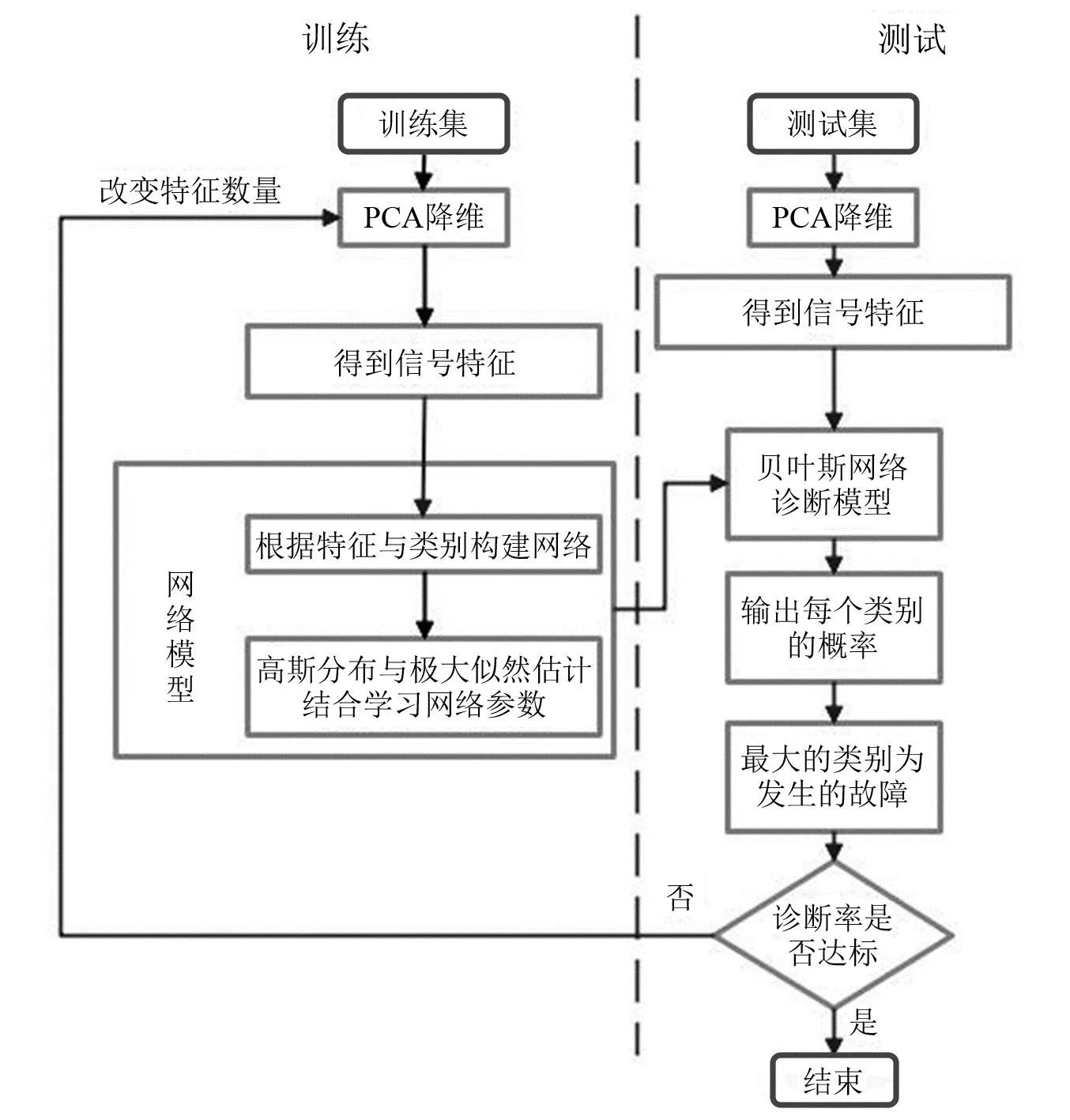
图5 流程图
步骤1选择数据集,划分样本、训练集以及测试集。
步骤2利用PCA对训练集样本进行降维,得到相互立的特征。
步骤3根据特征和类别建立贝叶斯网络结构。
步骤4用高斯分布和极大似然估计方法确定网络参数,得到贝叶斯网络诊断模型。
步骤5使用测试集样本对训练后的贝叶斯网络诊断模型进行测试。
步骤6判断诊断效果是否达到要求,如果达到要求,则结束;没有达到要求,改变PCA降维后得到的特征数量,返回步骤2,重新训练网络,然后测试性能。
3 试验分析
3.1 数据集
试验数据来自德国帕德博恩大学的滚动轴承状态监测的基准数据集,试验台由几个模块组成:①为电动机、②为扭矩测量轴、③为滚动轴承测试模块、④为飞轮和⑤为负载电机,如图6所示。将不同损伤类型的滚珠轴承安装在轴承测试模块中,生成试验数据,包含真实损坏(加速寿命试验)和人为损坏的两种数据,详细介绍见参考文献[29]。

图6 模块化的试验装置
在收集试验数据时同步测量了26种轴承损坏状态和6种未损坏(健康)状态的电机电流和振动信号,两种信号的采样率都为64 kHz。在所有的数据采集试验中,温度保持在45~50℃左右,每个信号都采集了四种工况下的数据,四种工况的运行参数如表1所示。

表1 不同工况的运行参数
3.2 振动信号故障诊断
3.2.1 不同少量样本下诊断结果
试验采用工况1(转速为900 r/min,负载转矩为0.7 Nm,径向力为1 000 N)工况下的真实损伤数据,选取数据集中的振动信号对所提出的PCA-BN模型验证。选择内圈故障点蚀单一损伤2级KI18、外圈故障点蚀单一损伤1级KA22和正常K002的数据进行试验,共两种故障和正常三种类型。
对每种类型下的原始数据采用重叠采样的方式进行划分,以1 500个采样点为重叠部分划分,每个样本有2 000个采样点。采用重叠采样的方法对于得到相同样本的数据集,所用的原始数据更少,相较于无重叠采样,更能体现所用数据少的特性。数据样本按1∶1的比例随机拆成训练集与测试集,用训练集训练模型,测试集来测试训练效果。
通过对原始振动数据采用重叠采样的方式划分得到两个不同样本数量的数据集,两个数据集的样本分布如表2所示。

表2 振动信号少量样本数据集
对数据进行PCA降维得到不同的特征数量后,分别进行试验验证,得到当取28个特征时,模型诊断效果最好,因此本文模型的特征节点为28个。通过对样本用PCA降维,得到28个特征,表示为F1,F2…F28。特征与故障类型间的贝叶斯网络结构图如图7所示。

图7 贝叶斯网络结构图
本文所提模型的条件概率服从高斯分布。在此次试验中,例如用极大似然估计求得μ16,外=0.5、σ16,外=0.2、第20个测试样本的第16个特征F16=1.3,此时在外圈故障下第16个特征F16的条件概率如式(10)所示
P(F16|外圈故障)=
(10)
为了保证准确性,对A、B两个数据集分别进行十次试验,求准确率平均值,试验结果如表3所示。由表3可知,在两个不同的少量样本振动信号数据集下,本文所提出的PCA-BNS模型均能达到较高的诊断效果,可以有效地对时序振动信号进行故障识别。说明在少量样本条件下,使用PCA的方法可以有效提取时序振动信号的故障特征;使用各个特征相互独立的条件可以有效解决针对一维时序信号进行贝叶斯网络建模困难的问题,使用特征相互独立的条件,建立的贝叶斯网络模型在少量样本条件下是有效的;使用极大似然估计得到先验概率以及使用高斯分布与极大似然估计结合去确定条件概率的方法,在针对时序振动信号构建的贝叶斯网络中,可以学习到有效的网络参数;贝叶斯网络在样本数据少的情况下,将样本数据集以条件概率的形式表示,可以充分挖掘到数据信息。
3.2.2 不同方法的诊断结果
用振动信号对几种经典诊断方法进行试验,本文选择了WT-BN、CNN[30]、LSTM[31]、SAE[32]作为对比模型进行试验,四个模型采用和本文方法相同的数据集(C,D)。WT-BN是由小波变换对原始数据进行特征提取,然后通过用评分算法去寻找特征和故障类型间的关系构建贝叶斯网络。堆叠式自编码器(stacked auto encoder,SAE)由三个自编码器堆叠而成,其中间层的神经元数量分别为800、200、50。SAE的超参数lr=0.005,batch_size=128。LSTM的输入维度为(128,2 000,1),得到(128,2 000,32)的时序特征,经过压平,输入到全连接层,得到(128,32)特征,最后经过softmax和全连接层得到分类结果。LSTM的超参数lr=0.01,batch_size=256。CNN模型输入(128,2 000,1)维数据到两层1DCNN中,经过sotfmax激活函数和池化,得到(128,38,16)特征,再通过平铺,drop操作和全连接层得到分类结果。CNN的超参数lr=0.01, batch_size = 128。诊断结果如图8所示。

图8 振动信号不同方法诊断结果
图8中纵坐标表示准确率,1表示诊断效果达到100%。从图8可知,本文所提PCA-BNs方法在A、B、C三个数据集下的诊断效果均优于以上几种诊断模型,说明本文所提方法在少量样本下较几种经典诊断模型,有明显的优势,可以有效解决因故障样本数据少而导致诊断准确率低的问题。
为了更好地展示本文模型的性能,本文使用 t-SNE算法将上述各模型最后一层的输出结果可视化。将模型在A数据集下的测试集上的输出使用t-SNE算法降维,并将结果显示在二维空间中,如图9所示。经过各个模型的特征提取,特征聚集到可以区分的状态。可以看出,本文模型基本实现了各故障状态的分离,而别的模型的并没有完全分离。

图9 各模型最后一层输出的t-SNE可视化分析:依次为PCA-BNS;WT-BN;LSTM;CNN;SAE
3.3 电流信号故障诊断
3.3.1 不同少量样本下诊断结果
为了验证模型的泛化能力,采用同工况下的电流信号对提出的PCA-BNs模型进行测试。选择内圈故障点蚀单一损伤2级KI18、外圈故障凹痕重复损伤1级KA30和正常K001的数据进行试验,共两种故障和正常三种类型。
通过对原始电流数据采用重叠采样的方式划分得到两个不同样本数量的数据集,两个数据集的样本分布如表4所示。

表4 电流数据集样本分布
为了保证准确性,对C、D两个数据集分别进行十次试验,求准确率平均值,试验结果如表5所示。

表5 电流信号准确率
由表5可知,在两个不同的少量样本电流信号数据集下,本文所提出的PCA-BNs模型均能达到较高的诊断效果,可以有效地对时序电流信号进行故障识别。说明在少量样本条件下,本文所提模型的泛化性能较好。
3.3.2 不同方法的诊断结果
用电流信号对几种经典诊断方法进行试验,选择了WT-BN、CNN、LSTM、SAE作为对比模型进行试验,模型结构同振动信号对比试验一致。四个模型采用和本文方法相同的数据集(C,D),诊断结果如图10所示。

图10 电流信号不同方法诊断结果
图10中纵坐标表示准确率,1表示诊断效果达到100%。从图10可知,本文所提PCA-BNs方法在C、D两个数据集下的诊断效果均优于以上几种诊断模型,并且达到较高的诊断率。而其他模型在电流信号下,相对于同样数据量的振动信号的诊断率下降了很多,说明这些模型的泛化性能较差。
为了更好地展示本文模型的在电流信号下的性能,本文使用t-SNE算法将上述各模型最后一层的输出结果可视化。将模型在C数据集下的测试集上的输出使用t-SNE算法降维,并将结果显示在二维空间中,如图11所示。经过各个模型的特征提取,特征聚集到可以区分的状态。可以看出,本文模型基本实现了各故障状态的分离,而其他模型并没有完全分离。
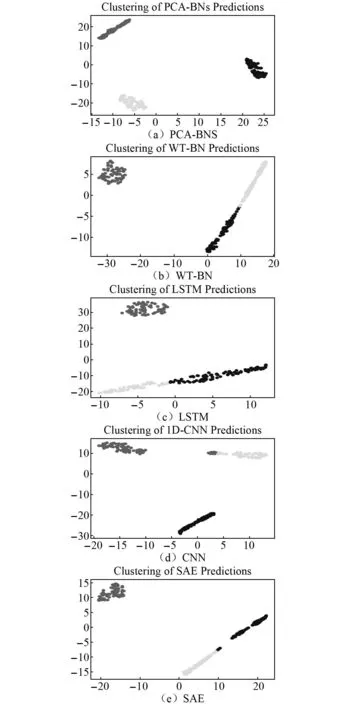
图11 各模型最后一层输出的t-SNE可视化分析:依次为PCA-BNS;WT-BN;LSTM;1D-CNN;SAE
3.4 不同方法的诊断时间
故障诊断不仅需要高的诊断准确率,实时性也是衡量故障诊断方法性能的一个重要指标。 因此对几种方法的时间也进行统计,统计时间为从划分数据开始到诊断出结果所用的时间,取10次运行结果的平均值,具体数值如表6所示。
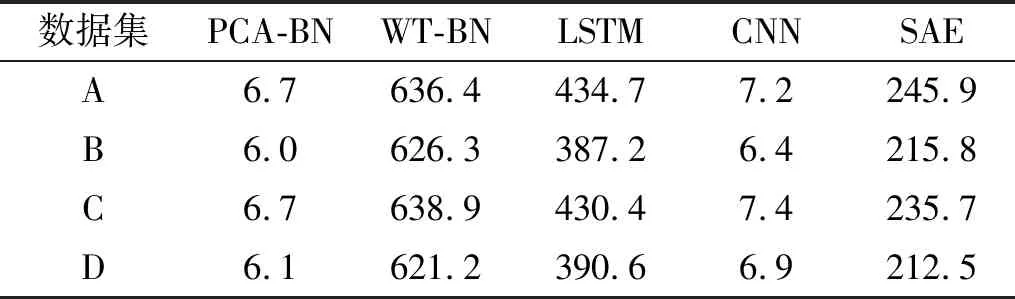
表6 不同方法所用时间
表6中数据是各方法在不同样本数据(A,B,C,D)下的运行时间。由表6可知,本文所提出的PCA-BNs方法用时最短,在故障诊断领域展现出较大的优势。这是因为本文用PCA降维,得到对类别都有影响的相互独立特征,直接可以得到贝叶斯网络结构,克服了传统贝叶斯网络因需要额外的算法构建网络结构而花费大量时间的弊端。
4 结 论
本文提出了一种基于贝叶斯网络的故障诊断方法。用主成分分析法和贝叶斯网络相结合的方法建立一维时序信号的故障诊断模型,旨在解决因有标签故障样本数据少而导致诊断准确率低的问题。在模型建立时,采用主成分分析法对一维时序信号进行降维,利用降维后的相互独立特征和故障类别首先建立单故障贝叶斯网络,然后融合单故障贝叶斯网络构建最终结构,克服BN建模中所需时间长的问题;并结合高斯分布和极大似然估计进行参数学习,得到少量样本下的故障诊断模型。以德国帕德博恩大学的电机数据为依据进行推理验证,并与几种经典的网络模型进行比较。结果表明,在两个振动信号数据集下,本文模型的诊断率均高于其他模型。在两个电流数据集下,其他模型诊断准确率普遍较低,而本文模型在两个数据集下的准确率分别达到0.980和0.943,较其他诊断模型具有明显的优势。并且本文算法的运行时间与其他方法相比得到了大幅缩减,在两个振动数据集下以及两个电流数据集下,从数据划分到诊断出结果仅用不足7秒的时间即可完成。
本文研究对一些工业设备,在普遍面临缺乏故障样本的情况下实现快速准确的故障诊断具有重要意义。但是,文中只进行了单工况条件下的诊断,下一步考虑进行多工况下的贝叶斯网络建模,实现多工况故障诊断。

