月球车与月壤交互作用的离散元-多体动力学耦合建模
徐 鸿, 雷 波, 刘锦阳
(上海交通大学 船舶海洋与建筑工程学院,上海 200240)
颗粒物质广泛存在于大自然中,如沙土、尘埃和稻谷等形状细小且分散的固体物质[1-2]。颗粒物质与人类的生产活动具有密切的关联,研究颗粒材料的介观与宏观性质对指导生产活动具有重要意义。为了描述离散单元之间的相互作用,基于离散元方法(discrete element method, DEM)[3]的数值仿真分析成为主要的研究手段之一,成为研究微观机理和宏观现象的有力工具。
在工程实际中,离散颗粒物质通常与周围环境相互作用,形成复杂的力学系统,呈现出复杂的力学特性,使其成为众多学科研究的热点之一。在机器人领域,适用于极端沙漠环境的仿生机器人已经引起了人们的广泛关注,如浅滩中游泳的蛇形机器人[4]、蜥蜴类仿生机器人[5-6]以及沙漠行走机器人[7-9]等。机器人与颗粒物质的相互作用研究揭示了二者之间的关联,对指导设计机器人机构有着重要指导意义。在航天领域,尤其是深空勘探中,需要研究地外星体的土壤特性,以设计出合理的航天任务计划。研究着陆器[10]、月壤钻取装置、采样车等对象与土壤颗粒之间的相互作用对于顺利开展航天任务有着至关重要的作用。
对于多体系统和颗粒系统之间的相互作用,可以采取工程试验或数值仿真开展研究。在某些情况下,开展工程试验存在困难,建立数值仿真模型是准确模拟这类颗粒物质与机械机构相互作用过程的有效途径。在不同的领域中,已经发展出了不同的耦合建模方法和数值算法,如用于描述多刚体系统与颗粒系统相互作用的多体系统-离散元耦合模型[11-13](multi-body dynamics-discrete element method,MBD-DEM)、模拟变形体与颗粒作用过程的有限元-离散元耦合模型(finite element method-discrete element method, FEM-DEM)以及使用光滑粒子流体动力学(smoothed particle hydrodynamics, SPH)方法模拟颗粒物质与多体系统相互作用的建模方法[14-15]。以DEM为代表的耦合模型具有更加高的精确性;以SPH为代表的建模方法具有更加高的效率。Rakhsha等[16]从多体和流体两个视角阐明了两种方法中颗粒流的参数之间的对应关系,对未来选择何种仿真手段来模拟颗粒介质具有重要的影响。
为了实现多体动力学和离散元的耦合仿真计算,有学者开发出如Adams/EDEM, RecurDyn/EDEM等协同仿真系统。虽然该耦合策略可行,但其跨平台间的数据传输存在一定的效率问题。Radjai等[17-18]通过耦合两个系统之间的动力学方程,采用高斯-塞德尔方法迭代求解状态变量,从而将两个系统的运动通过相互作用联系起来。这是一种强耦合的建模方法,采用优化算法进行迭代求解,具有较高的精度,但因收敛问题需要进行较长时间的迭代计算,从而导致仿真效率较低。对于大规模颗粒系统和多体系统之间的耦合计算,通常采用一种顺序求解过程,这是一种弱耦合策略。梁绍敏[19]建立了MBD-FEM-DEM的联合仿真模型,给出了有限元与离散元的耦合截面处理方法以及协同仿真的数据传输方式,并对着陆器在月壤的着陆性能进行了研究。Sanborn等[20]使用顺序耦合策略制定了标准颗粒接口(standard particle interface,SPI)将离散元程序与商业软件RecurDyn进行耦合。Wu等[21-22]利用该弱耦合策略对离散元和机械系统进行了耦合计算,并对机械装置的减震效果进行了研究。
总的来说,目前关于颗粒物质与多体系统的耦合研究还不够完善。对于耦合系统的仿真模拟需要依靠多平台协作,而平台之间的数据传输是影响计算效率的瓶颈。此外,耦合系统中物体的形状都比较规则,对于复杂形状的物体的碰撞检测研究开展较少,对于非光滑形状的物体的局部检测效率较低,有必要提出一种提高局部检测效率的方法。
本文的工作重点是建立复杂形状多体系统和颗粒系统耦合动力学模型,提出非光滑形状物体与颗粒之间的高效局部接触检测方法,并搭建多体系统和颗粒系统之间的耦合计算框架,实现同一个计算平台上进行耦合动力学仿真分析的功能。首先给出了颗粒系统的离散元建模方法、含约束多刚体系统笛卡尔建模方法以及耦合系统建模方法。然后用均匀网格进行全局检测,并对基于图的数据结构存储和检索接触信息进行改进,以降低时间和空间复杂度,在此基础上基于Hertz-Mindlin接触模型计算接触力。此外,为了提高非光滑形状物体与颗粒之间的局部检测效率,将非光滑形状物体离散为多个形状规则单元,提出分区域局部检测方法。将本文多体系统和颗粒系统耦合计算结果与试验结果进行对比,验证了耦合模型和算法的准确性。最后对月球车在月壤上行驶过程中的动力学问题进行研究,分析了不同驱动参数下的系统动力学特性以及不同轮胎形状对行驶运动的影响。
1 离散元-多体系统耦合建模
1.1 离散元系统动力学方程
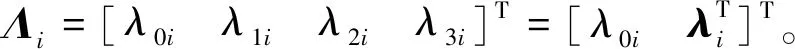
(1)
其中,
(2)
(3)
(4)
(5)

(6)
其中:
(7)
(8)
(9)
(10)

1.2 接触模型
在本文中,离散单元之间的接触力通过Hertz-Mindlin(HM)模型计算。HM模型接触力的表达式为[24-26]
(11)
(12)
(13)
(14)

(15)
(16)
式中,ρi和ρj分别为接触点相对物体Bi和Bj连体基基点的矢径。
1.3 接触检测
在进行大量物体的接触检测时,本文将检测过程分为全局检测和局部检测两个阶段。全局检测阶段将对物体与空间网格进行检测,将它们存入对应的空间网格;局部检测阶段将进行空间网格内的各个物体之间的形状检测。
1.3.1 全局检测
将空间计算域各方向划分成若干个子域,形成空间均匀网格,可以有效降低接触检测的复杂度[27]。如果不划分网格,那么局部检测的复杂度为O(N2);若合理选取网格的尺寸,可以将局部检测阶段的复杂度从O(N2)降低为O(N)。此外,全局检测阶段需要确定各个物体从属的网格编号,该阶段的复杂度为O(N)。
1.3.2 局部检测
针对像轮胎这样具有齿形的不规则形状的局部检测问题,本文提出分区域局部检测方法来缩减检测规模。采取拼接的方法组合成车轮的形状,如图1(a)所示。车轮由一个圆柱形状和八个长方体形状拼接在一起,长方体覆盖了部分圆柱表面,取而代之的是非光滑的长方体表面,剩余部分依旧是圆柱体光滑表面。这样组合成了齿状轮胎的非光滑表面。如图1(b)所示,在进行轮胎与颗粒的局部检测时,只需要对轮胎上的圆柱光滑部分、长方体非光滑部分和颗粒进行检测。采取这种分区域检测方法可以将齿状轮胎的各个子形状分散在不同的空间网格内,能够有效避免颗粒与轮胎其他部分不必要的接触检测,减少局部检测的次数,提高局部检测效率。综上所述,齿状轮胎和颗粒之间的接触检测问题可以分解为球与圆柱的局部检测和球与长方体的局部检测。下面详细介绍球和长方体以及球和圆柱体之间的局部检测。
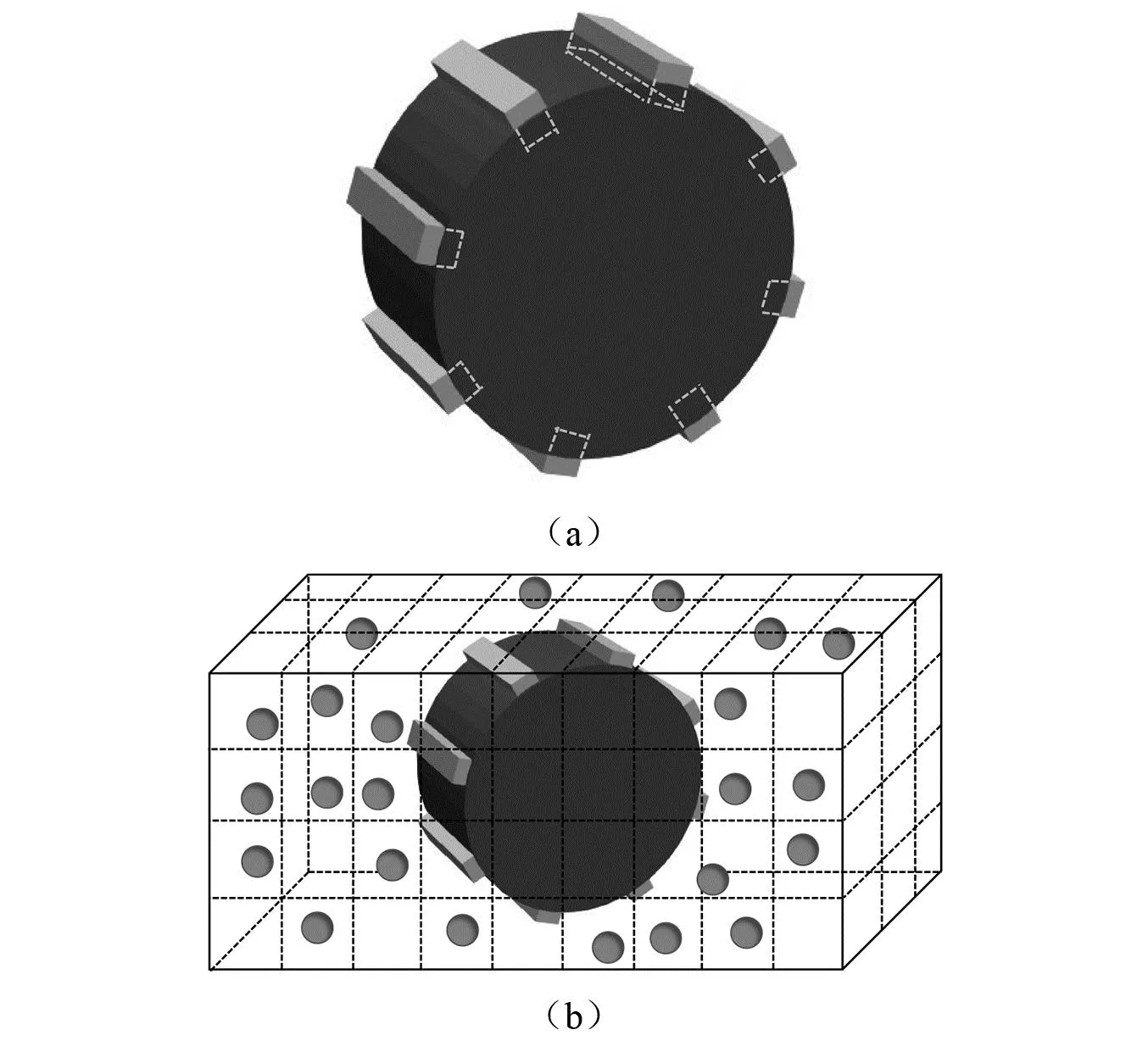
图1 轮胎接触检测示意图
1.3.2.1 球和长方体

图2 球和长方体示意图

图3 球和圆柱体示意图
定义clamp函数为
(17)
(18)
(19)
c2=p2+A2x
(20)
式中,A2为长方体的旋转矩阵,v=c2-p1。
1.3.2.2 球和圆柱体
定义函数Coeff(p,pm,pn)和Dist(p,pm,pn,μ)的计算式分别为
(21)
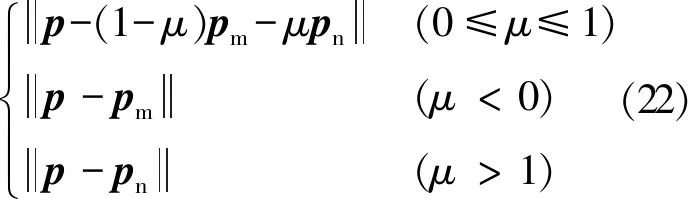

首先计算λ=Coeff(p1,pb,pt),其中,pb,pt为Pb,Pt点的绝对位置坐标阵,λ为球心在中轴线上的投影点的无量纲参数坐标,当λ=1时,投影点与Pt重合;当λ=0时,投影点与Pb重合。在此基础上计算球上的接触点和圆柱体上的接触点的绝对位置坐标。
(1)λ∈[0,1]
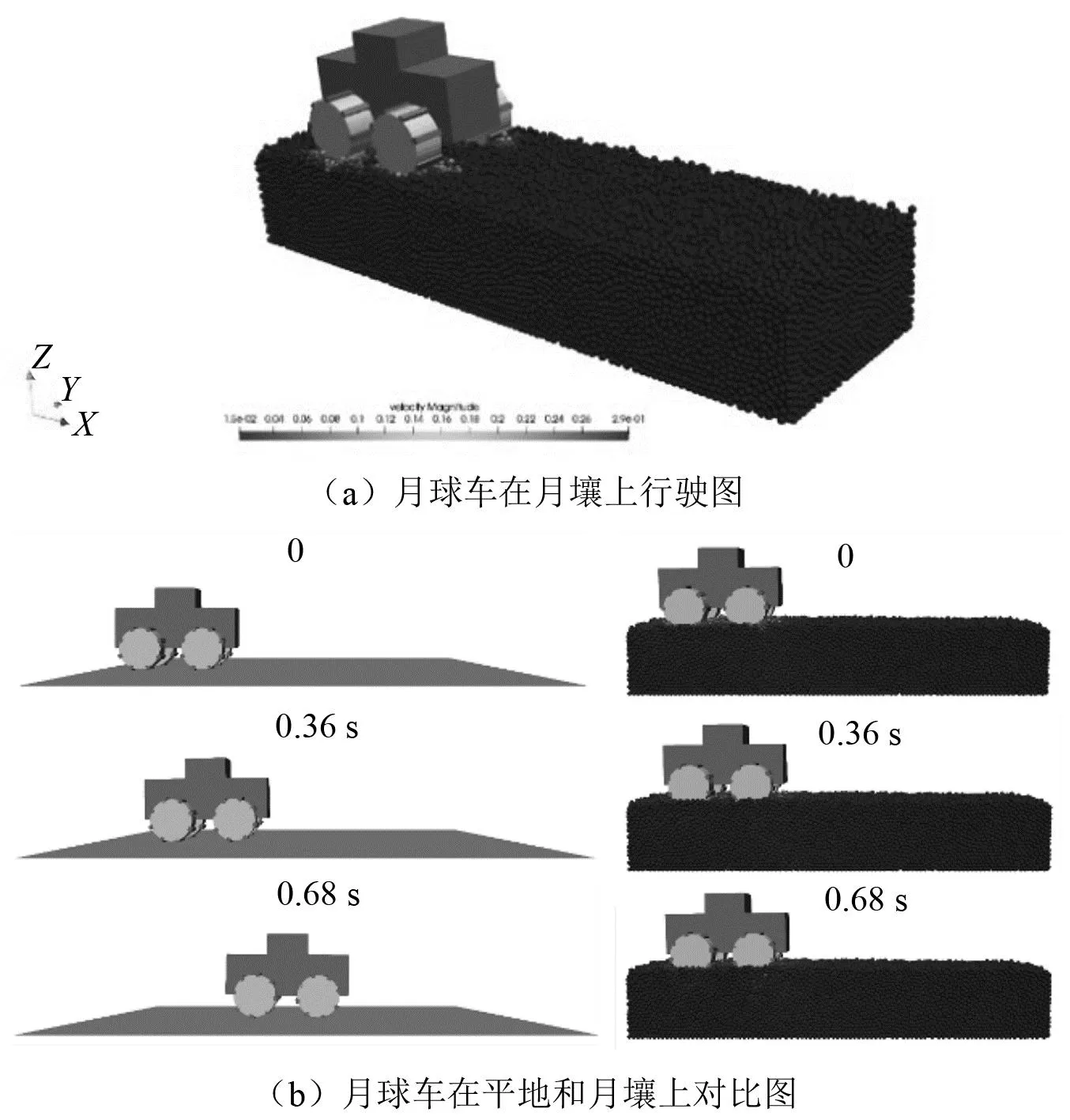
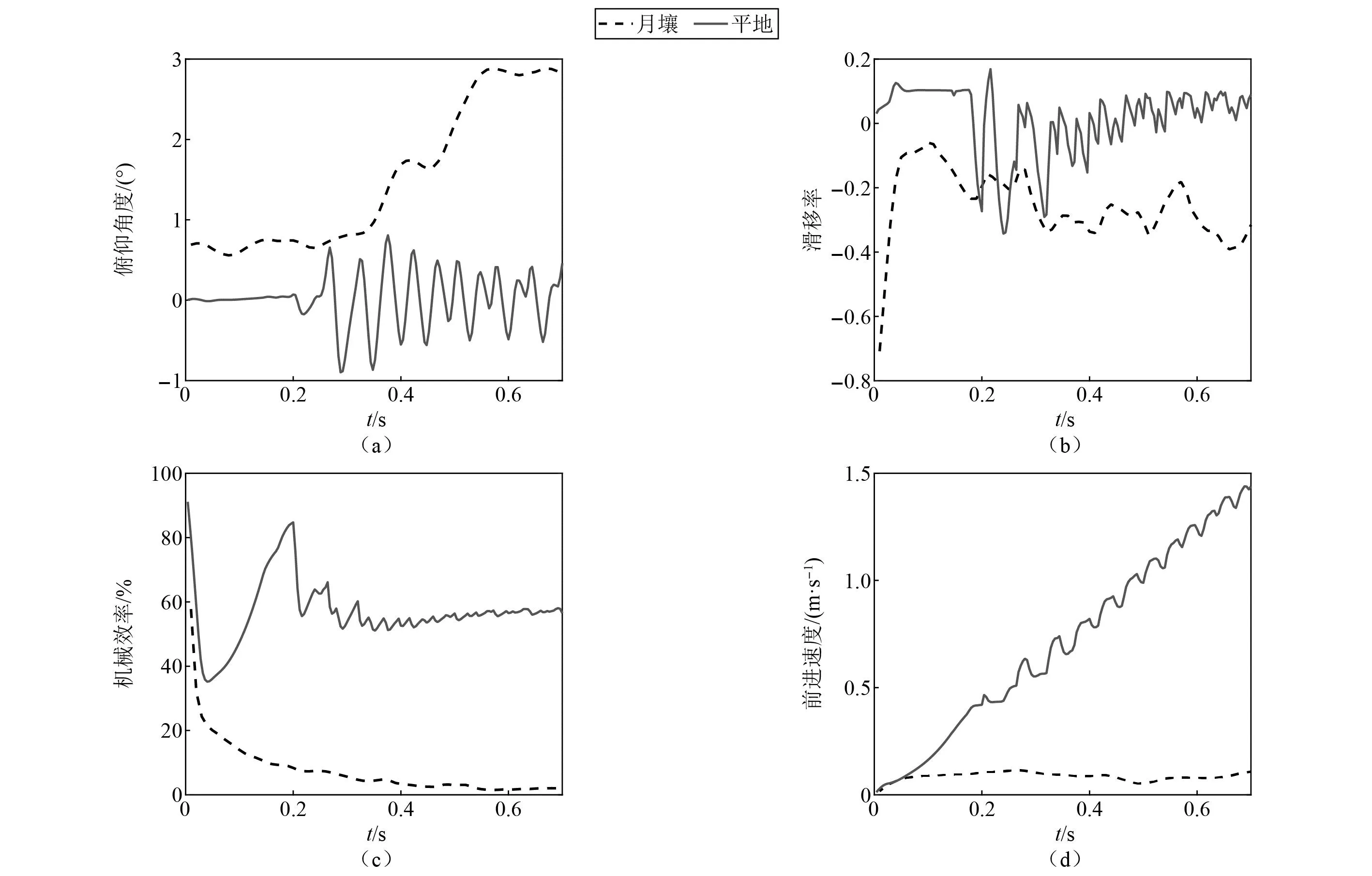
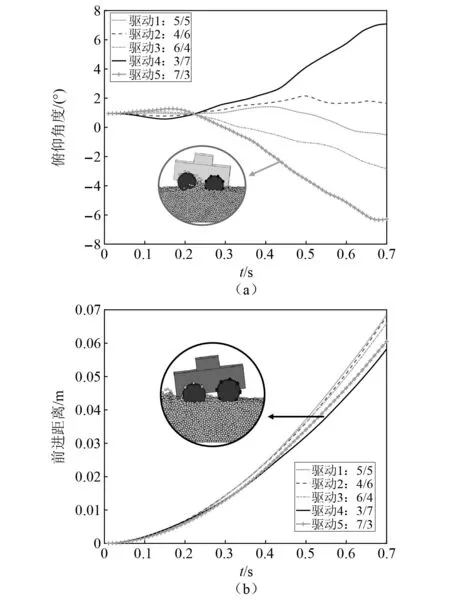
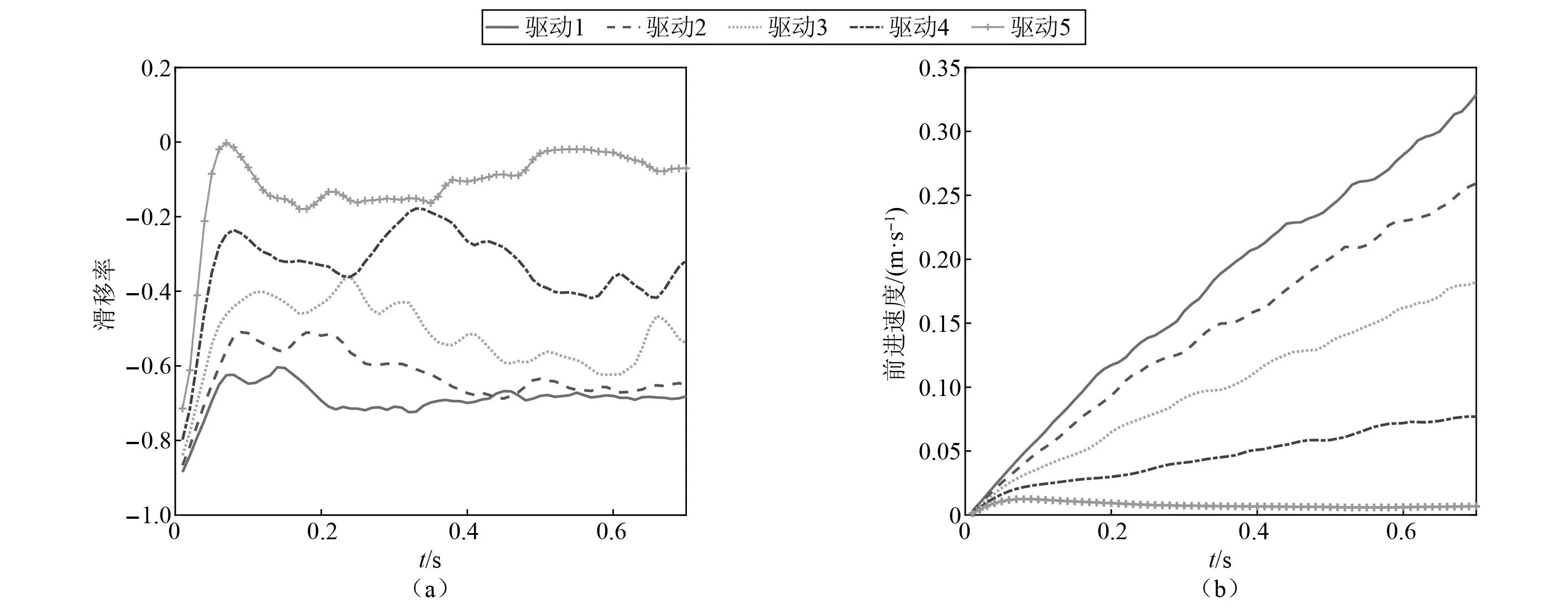
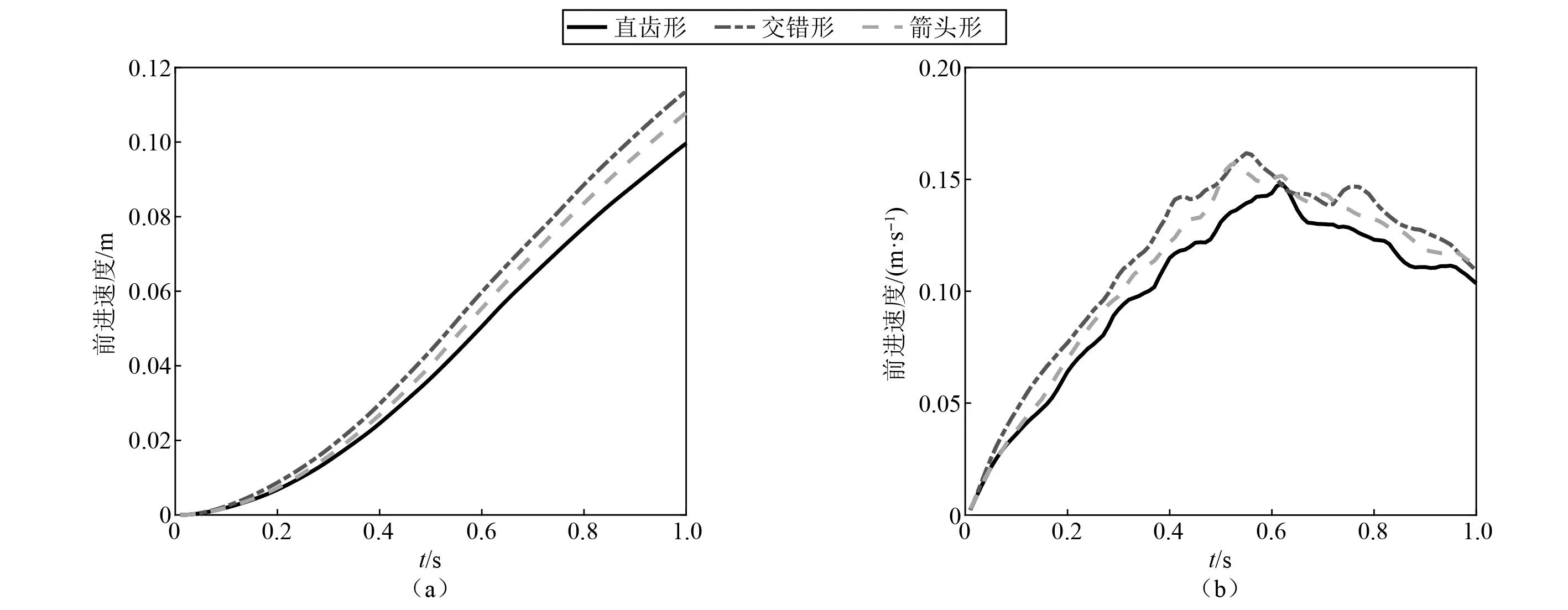
当λ∈[0,1]时,球心在圆柱中轴线上的投影点位于Pt,Pb两点之间,计算球心与投影点的距离d=Dist(p1,pb,pt,λ)。若d≥r1+r2,两个物体不相交,则不发生接触;若d (23) (24) 式中:v=p1-pH;pH=(1-λ)pb+λpt。 (2)λ∈(-∞,0)∪(1,+∞) (25) (26) 式中,v=p1-c2。 在接触力的计算过程中,需要用到上一步的历史接触信息。所以接触信息的检索查找过程是程序效率提升的关键。因为物体之间的接触关系的集合可以用拓扑图来表示,故本文采用改进的基于邻居链表的图数据结构存储物体之间的接触拓扑关系。在该接触图中,将物体作为顶点,接触信息作为边来储存。顶点用数组存储,边用链表结构链接在顶点上。此时查找顶点的位置是O(N)的复杂度,受哈希思想启发,通过在物体的数据字段内引入其所在接触图中顶点的序号,使得顶点的查找降为O(1)。因为空间中一个离散单元i与其他离散单元发生接触的数量是有限的,故查找该离散单元i的接触信息的复杂度为O(1)。该接触拓扑关系图中的接触信息的查找,修改,添加以及删除的复杂度降为O(1)。在基于HM模型计算切向摩擦力时,式(15)中包含切向位移,这是一个历史累积量,需要对历史接触信息进行查找,而在这种数据结构中查找接触信息的效率是O(1),故可以加速计算接触力。 (27) 多体系统的加速度约束方程为 (28) 式中,γ为加速度约束方程右项。 因引入了拉格朗日乘子项,故需联立加速度约束方程构成指标3微分代数混合方程(DAE-3)一起求解 (29) 求解式(31)时,需要对位形坐标阵和速度坐标阵进行违约修正,本文采用广义逆修正方法[28]对多体系统状态变量进行修正。 离散元和多体动力学耦合的方程表示为 (30) 为了兼顾效率和准确性,本文采取串联交错算法(conventional serial staggered,CSS)计算策略进行耦合计算,这是一种传统的顺序过程。该策略的耦合方式是引入一个通信系数n,在仿真计算过程中,每间隔n个离散元时间步长进行一次多体系统和颗粒系统之间的数据传递。具体的耦合过程如图4所示。 图4 多体系统和离散元系统耦合过程图 图5 耦合流程图 为了验证耦合模型以及耦合程序的正确性,对圆柱冲击颗粒算例进行了验证,文献[29]提供了试验数据对照。颗粒堆的材料参数[30]以及圆柱体的各项参数如下:颗粒半径rg=1 mm,密度ρg=1 200 kg/m3,弹性模量Eg=300 MPa,泊松比νg=0.7;圆柱体直径Dc=22 mm,高度Hc=22 mm,密度ρc=7 840 kg/m3,弹性模量Ec=205 GPa,泊松比νc=0.25;动摩擦因数μd=0.52,静摩擦因数μs=0.52,滚阻系数μr=0.7,恢复系数e=0.25。 圆柱体冲击颗粒堆的嵌入深度和嵌入速度的时间曲线如图6所示。由图6可知,圆柱体在冲击颗粒堆后速度急剧下滑,经过大约0.05 s后速度接近于0。圆柱体动能的耗散主要集中在前半段时间内,通过与颗粒之间的接触碰撞,一部分机械能转化为了颗粒的机械能,另一部分通过颗粒与物体以及颗粒之间的接触摩擦力耗散。从图6中可以看出,试验和仿真结果基本吻合,验证了离散元与多体系统耦合理论和耦合算法的准确性和有效性,为研究月球车在月壤表面行驶的动力学仿真奠定了基础。图7展示了圆柱体在冲击颗粒堆之后的动画过程。在圆柱体冲击颗粒堆的瞬时(t=0.01 s),表面颗粒产生了较大的向四周散开的速度,此时,处于下层的颗粒的速度较表面颗粒的速度较小,处于底部的颗粒速度几乎为零。随后,表面颗粒的速度逐步减小,当t=0.1 s时,大部分颗粒回落到颗粒堆表面。 图6 圆柱体冲击颗粒堆仿真与试验对比 图7 圆柱体冲击颗粒动画过程图 随着地外勘探和深空探测工程的发展,研究机械系统和颗粒系统之间的相互作用越来越迫切。对工程中的大量颗粒进行仿真是不现实的,本文采取粗粒化的方法对月壤进行模拟。月球车在月壤表面行驶的过程,表现出复杂的动力学行为,如图8(a)所示。本文以月球车为对象,研究其在月壤表面行驶过程中的动力学特性,给出具有工程参考价值的结论。图8(b)展现了月球车在平地上和月壤上不同的行驶表现,有必要对月球车在月壤上的行驶性能进行研究。 图8 月球车示意图 月球车在平地上行驶与在月壤上行驶呈现出完全不同的动力学特性。本文采用相同的驱动转矩,对月球车在平地上和月壤上行驶过程进行动力学仿真。图9给出了月球车在平地和月壤上行驶过程中的动力学响应的对比曲线。由图9(a)可知,在月壤表面行驶,车身会具有更大的俯仰角,这是因为月壤的表面更加松软,在月球车加速过程中,月壤作用于后轮的接触力较大,导致后轮的沉陷量大于前轮。为了对车轮打滑现象进行分析,定义滑移率为s=v/(ωr)-1,其中,v,ω为轮心的速度和轮子的角速度。图9(b)的滑移率对比可知,在月壤上行驶相较于平地上行驶,轮胎更加容易打滑。将图9(c)中的机械效率定义为η=100%×Ek/(MΔθ),即月球车的动能与输入转矩所做功的比,综合图9(d)对比可知,在平地上行驶的月球车具有较高的机械转化率和较高的前进速度,而在月壤上行驶的月球车,因为受到颗粒间的摩擦,颗粒与轮胎之间的摩擦以及一部分能量转化为颗粒的机械能等因素的影响,其机械效率和前进速度较低。在平地上行驶过程中的高频成分是因为轮齿周期性地与地面碰撞接触所致,而在月壤上行驶时,颗粒介质可作为缓冲消除因轮齿接触诱发的高频振荡。通过对比观察月球车在平地上行驶和月壤上行驶的过程,发现月球车在月壤上行驶的动力学特性与平地上有显著差异,姿态扰动和车轮打滑更加明显,机械效率和前进速度较低,因此,有必要设计具有较高的机械效率车轮,并有效控制姿态扰动。 图9 月球车在平地和月壤上相同驱动下动力学响应对比 月球车在月壤上行驶,前轮与后轮驱动力矩的比例会影响月球车行驶的距离以及姿态,通过调整合适的驱动力矩分配占比可以最大化的提高月球车前进的能力。所以本文对前后轮驱动转矩的不同分配比进行了仿真分析,维持总驱动力矩一致,对前后轮力矩分配比分别为5∶5、4∶6、6∶4、3∶7和7∶3的共五种分配方式进行了仿真模拟,结果如图10所示。 图10 月球车前后轮不同驱动比例对比 图10给出了月球车前后轮驱动配比不一致工况下的车身俯仰角以及前进距离曲线。从图10(a)中对比可以看出,在前后轮驱动比例相差过大的情况下,会出现轮胎陷入月壤过深的现象,导致车身的俯仰角过大。当前后轮驱动比例相差过大的时候,主驱动轮更加容易陷入月壤中,从而导致月球车前进困难。从图10(b)中对比可以看出,前后轮比例越接近的工况,月球车行驶的距离越远,这就意味着月球车受到的向前行驶阻力越小。对于月壤上行驶的月球车,由驱动转矩获得的机械能会因为颗粒与颗粒间、轮胎与颗粒间的接触摩擦而耗散,前后轮驱动比例相差越小,俯仰角越小,月球车向前行驶的阻力越小。综合考虑车身的平稳性以及前进的效率,本文选取前后轮驱动比例为4.5∶5.5作为文章后续的算例驱动分配参数。 当驱动力矩的大小发生变化时,月球车在月壤上行驶的动力学特性也会发生变化。所以本文对不同驱动力矩作用下的月球车行驶过程进行了仿真分析,采取五组不同的驱动,驱动1~5分别为作用在月球车前后轮上的力矩,驱动参数如表1所示,仿真结果如图11所示。 表1 五组驱动前后轮力矩分配参数 图11 月球车不同驱动转矩对比 图11给出了月球车不同驱动转矩大小下的轮胎滑移率以及前进速度对比。从图11(a)中可以看出,五种驱动情况下,在启动阶段轮胎的滑移率迅速上升,在经过一段时间之后,滑移率逐步下降并趋于稳定。驱动力矩越大,轮胎打滑的程度更严重。在驱动5情况下,当月球车具备一定速度时,其滑移率接近于零。从图11(b)中可见,更大的驱动转矩意味着增长更快的前进速度,驱动5的加速度接近于零,即驱动5的力矩大小恰好能够克服在该月壤上缓慢前进时的阻力,这意味着使该月球车在月壤上能够顺利启动的驱动转矩应该比驱动5的转矩大。由于其他四组驱动的转矩均大于驱动5,在四组工况下,月球车均以一定的加速度前进。对照图11(a)来看,驱动越大,前进加速度越大,但是轮胎打滑越严重,而打滑程度高意味着轮胎陷入月壤的概率更高,所以在月球车启动的时候,既要选择足够大小力矩的驱动使其能够启动,也要选择合适的驱动大小使得其具备一定的加速度且控制滑移率在一定范围之内,这样才能避免启动时轮胎深陷月壤导致任务失败。 轮齿的形状也是影响月球车前进的重要因素之一。故本文对三种不同形状的轮齿的月球车进行了数值仿真分析。根据上一小节的分析,为避免轮胎过度打滑,需要及时降低转矩,故采用的驱动模式为:当t≤0.5 s,施加驱动3的转矩分配,当t>0.5 s施加驱动4的转矩分配。三种不同形状的轮齿如图12所示,仿真结果如图13所示。 图12 三种不同形状轮胎 图13 月球车不同形状轮齿对比 图13给出了三种不同形状轮胎下月球车前进距离和速度的对比。观察对比图13(a)中月球车前进的位移曲线可知,对于轮胎形状为交错齿的情况,月球车在相同的驱动转矩作用下能够行驶最远的距离,这是因为交错齿形状相较于另外两种轮齿形状具有复杂的表面,从而能够提升月球车的抓地力,降低滑移率,使得月球车的前进效率更高。观察图13(b)可知,在经历了0.5 s的启动加速后,交错形齿状轮胎提速效果最好,在0.5~1.0 s的时间段内,随着驱动转矩减小,月球车的速度降低。 对比上一节驱动力的分析可知,采用驱动5的力矩大小是刚好能够使月球车在月壤上启动,而在此节的仿真结果中0.5~1.0 s的时间段内月球车速度降低而不是匀速,这就意味着维持月球车匀速前进的力矩大小与前进速度有关,并且前进速度越快,行驶遇到的阻力越大。总体来说,在相同驱动转矩作用下,交错形齿状轮胎的平均速度最大,行驶距离最长。 随着我国航天事业的不断发展,未来深空探测与地外星体勘探的任务越来越重要。本文以月球车为对象,用离散元方法对颗粒系统进行建模,基于Hertz-Mindlin接触模型计算颗粒与颗粒之间的法向接触力和切向摩擦力,并设计出一种改进的基于邻居链表的图数据结构来存储物体之间的接触信息,更节省空间和时间。采用多刚体笛卡尔动力学方法对月球车进行建模。针对齿状轮胎这种非光滑形状物体与颗粒之间的局部检测问题,将非光滑形状物体离散为多个形状规则单元,将轮胎形状的各个子形状分散在不同的空间网格内进行分区域检测,可以有效避免颗粒与轮胎其他部分不必要的接触检测,减小了局部检测的规模,从而化繁为简,提高了局部检测的效率。采用顺序耦合策略对颗粒系统和多体系统进行耦合动力学建模,在保证精度的同时缩减了计算规模。 首先对圆柱体冲击颗粒堆进行数值仿真,通过比较试验与仿真的结果,验证了本文构建的模型和耦合计算程序的正确性。在此基础上对月球车在月壤上行驶过程进行数值模拟和动力学响应分析。对比了月球车在平地上的动力学响应,说明了研究月球车在月壤上行驶的必要性。对于四驱的月球车,本文研究了前后轮驱动的配比对月球车在月壤上行驶过程中的影响,研究发现,前后轮驱动比例差距过大的情况下会导致月球车的轮胎更加容易陷入月壤中,车身的俯仰角会更加大,故选择前后轮驱动比例较小的驱动有利于提升行驶过程中的稳定性。在此基础上,本文还研究了不同驱动力矩大小情况下的月球车行驶动力学特性,给出了使月球车能够启动前进的最小力矩,并指出月球车启动时应对力矩进行适当控制以避免轮胎打滑。最后,对不同形状的轮胎花纹,采取相同的驱动力矩模式,研究轮胎花纹与月球车前进速度的关系。仿真结果表明,具有交错齿形的轮胎前进速度最快。 本文搭建了颗粒系统和多体系统的耦合仿真计算框架,实现了多刚体系统和颗粒系统之间的耦合计算,未来可研究柔性多体系统和颗粒系统之间的接触建模以及接触检测。在大规模颗粒系统的计算层面,本文采取了空间均匀网格来进行全局检测,使用改进的图数据结构进行接触存储以及CPU并行计算等数据结构和技术来提升计算效率,未来可使用GPU进行颗粒系统的大规模并行计算。对于月球车,可考虑增加悬挂和控制系统来进一步调节月球车在月壤上行驶的平稳性。目前,月球车在月壤表面行驶的过程尚无试验数据进行对比,月壤参数不明确,颗粒形状及尺寸尚未标定,故仿真结果仅供参考。1.4 接触存储
2 含约束多体系统动力学建模
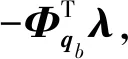
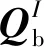
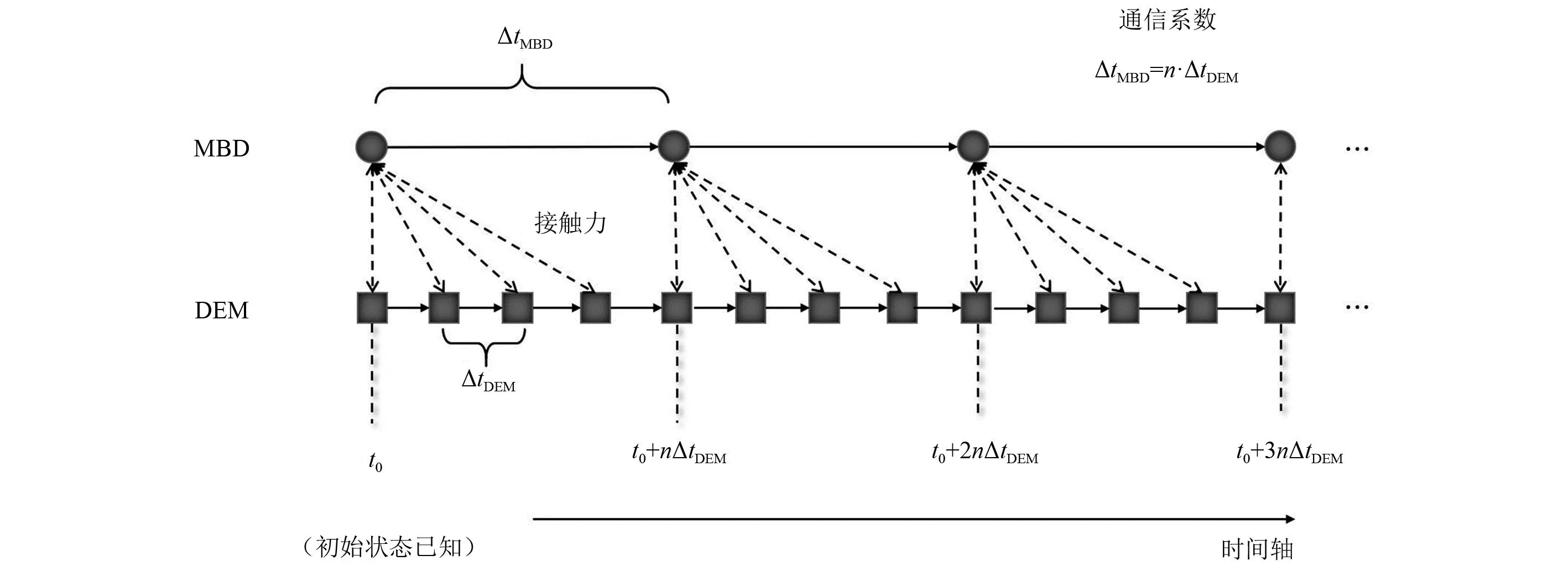
3 离散元-多体系统耦合算法
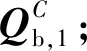

4 验证算例


5 月球车在月壤表面行驶的动力学仿真
5.1 月壤和平地上行驶动力学响应对比
5.2 驱动力矩分配的影响分析
5.3 驱动力矩大小的影响分析

5.4 轮齿形状的影响分析

6 结 论

