基于全局敏感性的自适应模型更新混合模拟方法
陈再现, 王纪伟,2, 钟炜彭, 刘 铖, 李明刚
(1.哈尔滨工业大学(威海) 海洋工程学院, 山东 威海 264209; 2.中建三局第一建设工程有限责任公司,湖北 武汉 430040)
混合模拟把计算机难以精确模拟的复杂非线性部分作为物理子结构进行真实的物理加载,其余部分作为数值子结构在计算机中建模计算,在20世纪70年代初由日本学者Hakuno等[1]提出,并在20世纪70年代中期由日本学者Takanashi等[2]第一次实现。混合模拟减少了试验成本和试验场地及设备的要求,并且也较为真实地反映了非线性较强构件的受力情况。因此被普遍认为是一种经济高效且极具有发展前景的新型抗震试验技术。
数值子结构的精确程度是影响混合模拟结果的重要因素。模型更新依据试验子结构反馈数据不断修正数值子结构,因此能较好地提升数值子结构的模型精度。近年来,模型更新备受众多学者关注。Yang等[3]首次将模型更新引入到混合模拟,利用神经网络对数值结构建模,通过试验子结构反馈数据不断修正神经网络,并在二层剪切模型中通过数值模拟和真实试验进行了验证。Elanwar等[4-5]以数值子结构和物理子结构的应力差值作为目标函数,对材料本构参数进行识别,数值模拟结果表明,基于材料本构模型参数的更新方法能提高混合模拟的精度。Yang等[6-7]分别开展了钢框架和钢筋混凝土桥墩的混合模拟工作,从材料本构模型层面对参数进行更新并验证了其对混合模拟精度的提升。Zhong等[8]提出采用均匀设计的方法对钢结构和钢筋混凝土结构材料参数进行识别,该方法极大地降低了样本数量,提高了识别效率,该方法在二层框架中以数值模拟的方式得到了验证。王涛等[9-10]提出统计容积卡尔曼滤波器的模型更新方法,并引入多尺度模型更新概念,通过二层带有自复位摩擦耗能支撑框架结构的数值模拟分析验证了方法的可行性。
模型更新首先依据寻优方法创造样本空间,然后利用试验子结构反馈数据确定最优样本点,最后更新至数值结构。从模型更新的过程来看,它是求解逆问题,根据试验子结构反馈数据识别多参数,样本空间的选取不当直接影响参数识别的效果。陈再现等[11-12]提出基于全局敏感性(global sensitivity, GS)的混合模拟试验方法,通过参数敏感度系数确定参数的搜索范围即样本空间能使参数更容易收敛到有效值。然而,在多参数识别过程中,仅通过固定的灵敏度系数去指导模型更新易导致参数陷入局部最优,从而降低模型更新的精度。基于此,将动量和自适应步长的概念引入模型更新中,提出基于全局敏感性的自适应(global sensitivity adaptive, GS-A)混合模拟试验方法在一定程度上弥补了仅用敏感度系数确定样本空间的缺陷,提升了参数收敛的速度和模型更新的精度。下文通过介绍所提出方法的基本原理、用以验证该方法的数值模型和更新参数的选择以及数值模拟方案,通过33个数值模拟算例验证本文方法的有效性。
1 GS-A混合模拟模型更新方法基本原理及流程
1.1 基本原理
陈再现等推出的GS模型更新混合模拟方法使用均匀设计选择样本空间时,以上一步最优参数为搜索中心,各参数搜索步长与对应的敏感性系数成正比,利用相应的均匀设计表[13]生成验算子结构样本空间。
然而在参数识别过程中,若固定中心点(上一步最优参数组合),创建样本空间,对当前步最优参数进行搜索,会出现与参考模型差异较大的参数不能迅速被识别,设置落入局部最优点,因此基于全局敏感性的自适应(GS-A)模型更新混合模拟方法引入动量概念,即参考历史参数变化,引导参数朝着最优值更快收敛,动量表达式为
(1)
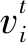
在参数识别的最初阶段,参数组合距离目标函数的最优解距离很远,但是随着参数识别的次数变大,参数组合会越来越接近最优解,因此本文提出对搜索步长进行自适应处理,依据每个参数的变化量大小来调整各个参数的步长,使参数组合在接近最优解时,步长将适当缩小,使参数组合更加趋近于最优解。自适应步长计算公式见式(2)~式(3)
(2)
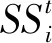
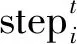
(3)
式中,ε为维持数值稳定性所添加的常数,本文取为10-8。
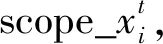
(4)

(5)
式中,TSi为t时刻,第i个参数的总阶灵敏度系数。
1.2 基本流程
数值模拟所采用的数值模型[14]由全结构数值模型、物理子结构和验算子结构三部分组成,如图1所示上部三个部分。将地震激励输入到全结构数值模型,通过时程分析获取当前步的内力和位移,并输入到物理子结构和验算子结构中,获得恢复力,不同的是,物理子结构的恢复力为参考目标,验算子结构是物理子结构的数值模拟空间(通过优化算法选择),两者除更新参数外均相同,依据目标函数选取与物理子结构恢复力误差最小的验算子结构,将其参数更新到计算全结构中,从而进行下一地震步的计算。如图1所示模型更新基本流程,具体步骤如下:

图1 模型更新流程图
步骤1利用动力时程分析求出数值全结构结构响应,提取出子结构划分界面处的位移及内力(界面位移yps,轴力Nps和弯矩Mps),并发送到物理子结构和验算子结构。
步骤2物理子结构和验算子结构接收到位移与内力,完成加载后得到各自的恢复力,并根据误差判断规则,选择是否启动更新程序,目标函数选取与物理子结构恢复力误差最小的验算子结构,如式(6)所示,如果启动,进入步骤3,如果不启动,返回步骤1进行下一步动力时程分析。
步骤3依据式(4)所确定的参数搜索范围,利用均匀设计得到验算子结构样本空间,识别程序比较样本空间中多个验算子结构与物理子结构恢复力的相对累积误差,选出误差最小的验算子结构,将其参数组合作为更优参数组合发送到全结构数值模型进行参数更新,并进行下一步动力时程分析。
步骤4直到地震动记录结束,终止程序,否则,重复步骤1~步骤4。
(6)
式中:Rps(i)为物理子结构恢复力,作为参考值;Rys(i)为验算子结构恢复力。
2 数值模拟方案
2.1 基本模型构建
选用一榀二层一跨的钢框架框结构,一层和二层高度分别为3 600 mm和3 000 mm,跨度6 000 mm,框架几何尺寸、质量及荷载分布如图2所示,质量及荷载分布参照GB 50011—2010《建筑抗震设计规范》与GB 50009—2012《建筑结构荷载规范》计算所得,截面信息分别如图2和图3所示。
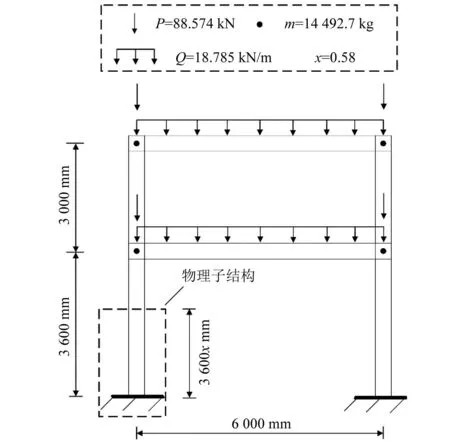
图2 框架模型
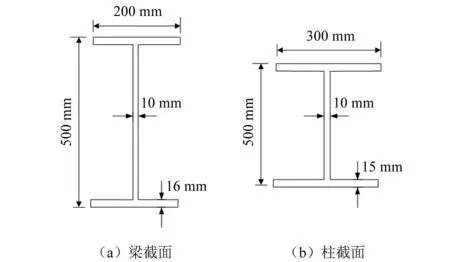
图3 钢框架截面
物理子结构与数值子结构的界面设置在弹性反弯点处[15],由D值法计算得到钢框架的反弯点分别为底柱长度的0.58倍处,如图2所示。采用OpenSees有限元软件进行数值建模,钢材本构模型采用双线性模型(Steel01),模型假定基础与地基刚性连接,框架结构采用基于力的非线性梁柱单元(nonlinear beam-column element),每个单元选取5个Gauss-Lobatto,截面为纤维截面。
2.2 更新参数确定及模拟方案
选用双线性钢材本构模型(Steel01),更新参数为8个:弹性模量Es,屈服强度fys以及硬化系数bs,尺寸参数为高度h、宽度d、腹板厚度t1和翼缘厚度t2,以及柱长ls。参数的参考值设置如表1所示,将各个参数比例化,设定参数的参考值为1,模型的材料误差参数浮动范围设为(0.7~1.3),尺寸误差参数浮动范围设为(0.98~1.02)。
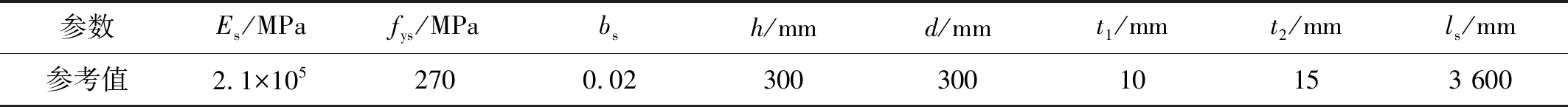
表1 钢结构参数参考值

表2 初始参数组
为验证GS-A方法模型更新效果,把不更新混合模拟(hybrid simulation,HS)和GS模型更新方法作为对照组。HS用于反映传统混合模拟中各参数是带有误差的统计值的情况并且在试验过程中参数不被更新。GS方法和GS-A方法分别为在混合模拟中采用基于全局敏感性的模型更新方法和基于全局敏感性的自适应模型更新方法,在试验过程中参数不断地被更新。数值模拟方案如表3所示。

表3 数值模拟方案
3 数值模拟结果
各参数对一层位移相对累计误差的敏感性在地震的各个时间段是不断变化的,因此对试验模型参数进行分阶段敏感性分析,并以此结果作为模型更新验算子结构样本空间选择的依据,敏感性分析方法采用Sobol法[16]。设置地震峰值加速度( peak ground acceleration,PGA)为510 gal的El Centro波作为地震激励,取持续6 s的地面运动记录,积分步长取0.01 s。地震分阶段灵敏度系数变化如图4所示。根据Sobol分析结果,在结构处于弹性阶段时(2 s之前),参数弹性模量和翼缘宽度的敏感度系数最大,在结构经历塑性阶段时(2 s之后),参数屈服强度敏感度系数开始增大,屈服强度、弹性模量和翼缘厚度的敏感性排名前三。
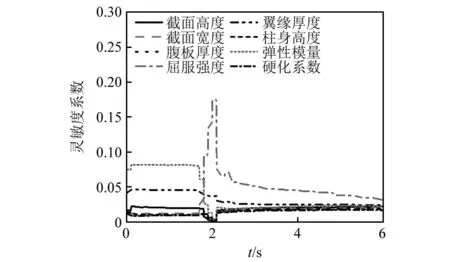
图4 地震分阶段钢框架模型参数灵敏度系数变化图
参考解(Ref)是模型参数为参考值时的时程分析结果。对照组分别为参数不更新时混合模拟(HS)的结果和采用基于全局敏感性(GS)的模型更新方法进行模型更新的结果。采用物理子结构位移相对累积误差和峰值位移相对误差作为模拟结果精度的评价指标,分别如式(7)和式(8)。
(7)
式中:yref(i)为物理子结构位移参考值,由时程分析得出;yps(i)为物理子结构位移。
(8)
式中:y_maxref为物理子结构峰值位移参考值,由时程分析得出;y_maxps为物理子结构峰值位移。
钢框架模型更新效果如图5所示,在11个初始误差参数组中,相对于HS,使用GS-A方法和GS方法更新完成后模型的物理子结构处位移时程与参考位移时程的相对累积误差均有所降低,并且,两种模型更新方法对峰值位移相对误差均有所改善,但是GS-A更新效果明显优于GS,GS-A物理子结构处位移的相对累积和峰值位移相对误差均在5.7%和2.7%以内,而GS在案例7中甚至达到了52.9%和28.4%;11个初始误差参数组中,GS-A方法和GS方法的物理子结构处位移的相对累积误差和峰值位移相对误差的均值和提升效果如表4所示,GS-A方法物理子结构处位移的相对累积和峰值位移相对误差的均值为2.3%和1.3%,均优于GS方法的17.8%和9.4%,相对于HS,分别提升了97.1%和96.6%,提升效果均优于GS方法的78.3%和74.5%。

表4 模型更新提升效果
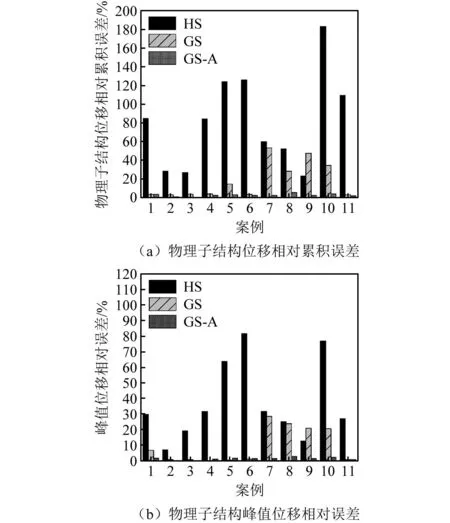
图5 钢框架(steel01本构模型)更新效果图
GS方法和GS-A方法对11个初始误差参数组的参数识别结果的平均误差如表5所示,表中按参数敏感性由大到小排序。可见,GS-A方法的参数识别误差相对于GS方法有所降低,值得注意的是,对于敏感性最小的硬化系数bs,GS-A方法能有效识别,且平均误差仅有1.3%,GS方法则识别失效,平均误差达到27.9%。

表5 模型更新后参数平均误差
GS方法和GS-A方法在模型更新后段(4~6 s)中各参数的平均相对误差和标准差如表6所示,表中按参数敏感性由大到小排序。GS-A方法参数平均相对误差均小于2.3%,而GS方法对敏感性较大的参数弹性模量的识别平均误差达到4.9%,对于敏感性较小的硬化系数平均误差达到27.9%。对于参数识别过程的标准差,GS-A方法均小于GS方法,因此GS-A方法的稳定性明显优于GS方法。

表6 模型更新(4~6 s)参数平均误差和标准差
在11个案例中,案例9所对应的GS方法的位移的相对累积误差和峰值相对误差均比HS大,以此选取案例9的参数识别过程、位移时程与滞回曲线对比示例。
案例9的参数识别过程对比如图6所示,GS方法和GS-A方法在模型更新后段(4~6 s)中各参数的标准差如表7所示,GS-A方法的标准差均低于GS方法,因此GS-A方法的参数识别的稳定性优于GS方法。值得注意的是,在GS方法中,各参数在识别过程中不断上下波动,说明参数陷入局部最优值,从而来回震荡,反观GS-A方法,动量使样本空间中心向参数变化方向移动,参数更快地收敛,自适应系数调整样本空间的范围,防止参数组合陷入局部最优。GS方法和GS-A方法参数最终识别值与参考值的比值如表8所示。由表8可知,GS-A方法的参数识别误差相对于GS方法均有所降低,提升了模型更新精度。

表7 模型更新(4~6 s)参数标准差(案例9)

表8 参数最终识别值与参考值比值(案例9)
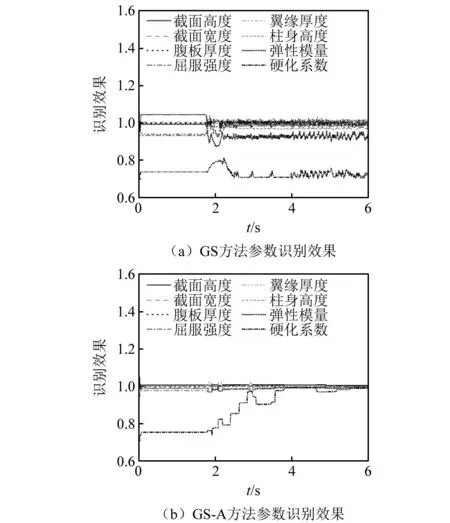
图6 参数更新效果图(案例9)
案例9的物理子结构位移时程和滞回曲线对比见图7和图8,GS-A方法的位移时程曲线和滞回曲线相对HS和GS方法更贴近于参考解(Ref)。GS-A方法的物理子结构位移与参考解的相对累积误差为2.27%,远小于HS的23.05%和GS方法的47.16%,因此GS-A方法显著地提升了模型更新效果。
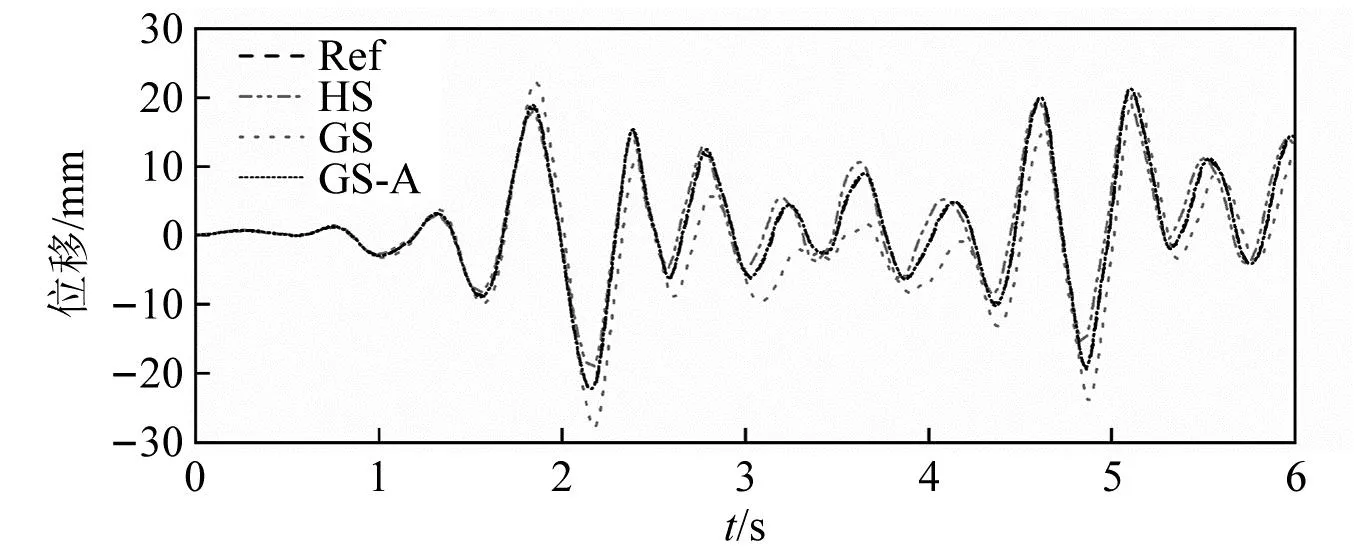
图7 位移曲线对比图(案例9)

图8 滞回曲线对比图(案例9)
4 结 论
(1)提出了GS-A模型更新混合模拟方法,在钢框架中进行了11种不同初值参数误差组的数值模拟用以验证该方法的适用性,验证了动量和自适应策略的可行性。模拟结果显示,GS-A方法的相对累积误差和物理子结构峰值位移相对误差的均值分别为2.3%和1.3%,相对于GS方法的17.8%和9.4%有显著提升,改善了模型更新效果。
(2)在参数识别精度方面,在GS方法中敏感性较大的参数弹性模量的平均相对误差达到了6.0%,敏感性较小的参数硬化系数识别效果欠佳,平均相对误差达到了27.1%,而GS-A方法各参数的平均相对误差均在1.4%以内,GS-A方法相对于GS方法有效地提升了参数识别的精度。
(3)在参数识别后段(4~6 s),GS-A方法中的各参数标准差平均值均小于GS方法,因此GS-A方法提升了参数识别的稳定性。
(4)案例9中,GS方法参数组合陷入局部最优解,因此导致模型更新效果比不更新还差。GS-A方法解决了参数陷入局部最优解的问题,参数识别效果的精度和稳定性均优于GS方法,且位移时程和滞回曲线相对于HS和GS方法均更贴近于参考解,物理子结构位移相对累积误差仅有2.3%,显著地提升了模型更新效果。

