基于精细传递矩阵法的气囊隔振器横向刚度特性分析

成玉强, 蔡存光, 高 华, 帅长庚

(1. 海军工程大学 振动噪声研究所,武汉 430033;2. 船舶振动噪声重点实验室, 武汉 430033)

气囊隔振器,具有低固频、大承载、无蠕变、气压可调、性能可控等优点,其作为一种性能优异的隔振元件已经广泛应用于车辆以及船舶隔振领域中[1-3]。受限于舰船舱室内部狭小有限的安装空间以及浮筏隔振装置高达上百吨的支撑质量,舰用气囊隔振器的工作压力通常较高,一般为同规格车用气囊隔振器的3倍以上[4]。为保证舰用气囊隔振器在较高工作压力条件下的可靠性,其一般采用稳定性更强的单腔室结构设计且囊体结构大大增强。

刚度特性是气囊隔振器的基本力学特性,可依据气囊隔振器的受力方向分为垂向刚度特性和横向刚度特性。垂向是气囊隔振器的承载方向,一般认为垂向刚度特性是由内部压缩气体在垂向变形过程中产生的反向作用力决定,囊体自身产生的作用力对垂向刚度特性的影响较小,在气囊隔振器垂向刚度特性的简化计算模型中通常可以忽略囊体作用力的影响[5-6]。气囊隔振器的水平方向并非承载方向,其囊体在横向变形过程中自身产生的反作用力较大而无法忽略[7-8],且在舰用气囊隔振器囊体结构强度大大增强的条件下,囊体刚度在横向刚度特性中将占据主导位置,因此为分析气囊隔振器的横向刚度特性,必须构建并求解气囊隔振器的囊体力学模型。

气囊隔振器橡胶囊体一般由内、外橡胶层和中间纤维骨架层组成,是一种纤维增强橡胶基复合材料,具有典型的各向异性特征,其力学模型构建及求解十分复杂[9]。当前关于气囊隔振器刚度特性的理论研究主要集中于内部气体模型上[10-12],对于囊体力学模型的构建,则多采用等效简化、数值仿真或系数拟合等方式进行,如Erin等[13]以线性弹簧、阻尼器以及迟滞阻尼器并联的方式等效模拟了具备非线性力学特征的囊体力学模型,求解并分析了气囊隔振器的刚度特性;Chen等[14]提出了一种包含结构参数预测模型和橡胶囊体模型的气囊隔振器刚度模型,其中橡胶囊体模型是由分数式开尔文-沃格特模型和平滑摩擦模型组成的非线性等效简化模型;Zhu等[15]建立了一种通用的气囊隔振器力学模型,不仅考虑了内部气体热力学的贡献,也考虑了囊体橡胶的摩擦和黏弹性效应,该模型的特点是在保持Berg光滑摩擦模型的基础上,通过统计方法得到了位移激励标准偏差,并以此确定了摩擦模型参数,求解了气囊隔振器的刚度特性;Qi等[16]基于气体热力学方程推导了气囊隔振器气体刚度特性的参数表达式,关于囊体刚度计算则采用对数值仿真结果进行曲线拟合的方法开展,最后通过样机试验验证了所建立刚度模型的有效性;袁春元等[17]利用Yeon模型以及Rebar单元构建了纤维增强橡胶囊体的仿真模型,并基于流固耦合边界条件设定了橡胶囊体与内部气体之间的分界面,通过对比数值仿真计算结果与气囊隔振器力学特性的一般规律,验证了构建模型的有效性。

综上,现有关于气囊隔振器刚度特性的理论研究一般是基于气体的热力学方程,以等效简化、数值仿真或系数拟合等方式构建起囊体力学模型,再结合几何结构参数变化方程开展的计算分析研究,尚未完全构建起横向刚度特性的参数化计算模型。

本文基于壳体理论建立了预载条件下的气囊隔振器的囊体力学模型,通过精细传递矩阵法求解得到了囊体状态向量,采用迭代法解析了向量参数间的耦合关系,结合理想气体理论模型,完成了气囊隔振器横向刚度特性的参数化求解与分析。

1 横向刚度特性理论模型建立及求解

气囊隔振器横向刚度特性可由气体刚度以及囊体刚度组成,刚度表达式为

K=KQ+KN

(1)

式中,KQ、KN分别为气体刚度和囊体刚度。目前大量学者针对气体刚度的理论模型已经开展了深入且细致的研究,建立了较为准确的气体刚度参数化计算模型,横向气体刚度的参数表达式为

(2)

式中:Re、P分别为气囊隔振器的有效半径和内部气压;α为导向角度。

为保证舰用气囊隔振器在高内压作用下的可靠性,囊体选用具有较高弹性模量的纤维材料,且纤维缠绕层厚度也随之提高,因此舰用气囊隔振器囊体在横向变形过程中,其自身产生的反作用力大大提高,囊体刚度特性也随之明显提升,已经成为气囊隔振器横向刚度特性中的主导因素。因此,为完成气囊隔振器横向刚度特性的参数化求解,必须建立囊体刚度特性的参数化计算模型。

1.1 囊体力学模型建立

气囊隔振器结构如图1所示,主要由上安装板、下安装板、导向座、橡胶囊体以及约束套筒组成,其中约束套筒与橡胶囊体直线段接触。气囊隔振器在工作过程中,内部压缩气体需达到较高压力P来承担设备荷载F,此时囊体直线段在高压状态下与约束套筒贴合,囊体圆弧段沿导向座发生卷曲变形。因此,气囊隔振器的囊体刚度主要取决于囊体圆弧段在变形过程中的力学状态,囊体直线段在刚度求解过程中可忽略。

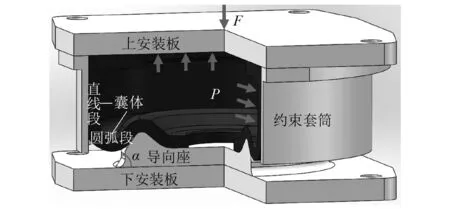
图1 气囊隔振器结构示意图

现忽略囊体直线段作用,并将圆弧段囊体简化为一旋转壳结构,该旋转壳是由一平面曲线绕与此曲线共面的一轴线旋转而成,如图2(a)所示。取旋转壳上一单元,如图2(b)所示,壳体上任意点均可用曲面坐标(φ,θ)表示,φ为经线方向,θ为纬线方向,相应的主曲率半径分别用Rφ和Rθ表示,纬线面相应的曲率半径用R0表示,则旋转壳的拉梅系数为R0和Rφ,由几何结构关系可得

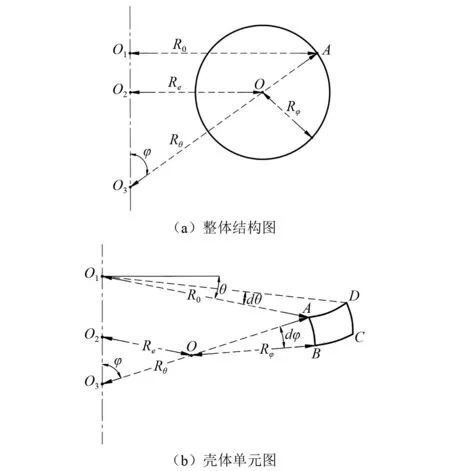
图2 旋转壳几何结构示意图

(3)

平衡状态下气囊隔振器的外部预载力F与内部压力P之间的函数关系可简化表示为[18]

(4)

假设预载条件下气囊隔振器囊体经线和纬线方向上单位长度截面上的预应力分别为Nφ0和Nθ0,根据式(4)以及薄壳理论进行分析,可得到囊体预应力的简化表达式为[19]

(5)

囊体的力学状态可由几何方程、物理方程以及平衡方程确定。现将u、v、w作为位移分量;εφ、εθ和εφθ作为位移应变分量;χφ、χθ和χφθ作为弯曲应变分量;κφ、κθ作为曲率分量;Nφ、Nθ和Nφθ作为内力分量;Mφ、Mθ和Mφθ作为弯矩分量;Qφ和Qθ作为剪力分量。则囊体的几何方程为[20]

(6)

气囊隔振器囊体本质上是一种橡胶基纤维增强复合材料,由橡胶和纤维交替铺层缠绕形成,可根据复合材料理论得到囊体的物理方程为[21]

(7)

式中:Aij为拉压刚度;Dij为弯曲刚度,拉弯刚度系数的表达式为

(8)

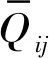
(9)

式中:δ为纤维缠绕角度;Qij为材料主方向的刚度系数。Qij的表达式为

(10)

式中,E1、E2为纤维增强复合材料1,2主方向上的弹性模量,υ12和υ21为纤维增强复合材料1-2方向和2-1方向上的泊松比,G12为纤维增强复合材料剪切模量。材料主方向1为沿纤维轴向方向,材料主方向2为沿纤维横向方向。

如图3所示,气囊隔振器囊体的成型过程分为芯模纤维缠绕阶段和囊体挤压成型阶段,其内部的纤维缠绕轨迹线型也由上述两阶段决定:在图3(a)所示的芯模纤维缠绕阶段中,纤维通过非测地线缠绕方式缠绕至囊体成型芯模上,形成纤维缠绕轨迹初次分布线型;在图3(b)所示的囊体挤压成型阶段中,囊体锥形段受力挤压形成囊体圆弧段,纤维缠绕轨迹初次分布线型发生缠绕轨迹微变化,形成最终的纤维缠绕轨迹线型。前期作者依据非测地线缠绕理论以及纤维交叉稳定假设构建起囊体不同位置处的变缠绕轨迹方程[23],将变缠绕轨迹方程代入式(9)中,并结合式(7)、式(8)以及式(10)即可得到具备变缠绕轨迹特征的物理方程。

图3 纤维一体化缠绕增强囊体主要成型阶段

由于气囊隔振器的工作过程一般在内部压力以及外部预载的共同作用下进行,为求解囊体刚度特性,在构建囊体平衡方程时,应考虑预载作用下气囊隔振器囊体中的预应力。通过分析引入囊体预应力后气囊隔振器平衡方程中应力、应变的变化关系,在忽略三阶微量以及两阶扰动量的条件下,基于Flügge理论[24]推导预载条件下的囊体平衡方程为

(11)

1.2 囊体状态向量传递矩阵推导

假设气囊隔振器的囊体状态向量为Z(φ),由囊体位移及内力状态量组成,表达式为

Z(φ)=[uvwκφNφSφVφMφ]T

(12)

式中,Sφ和Vφ分别为Kelvin-Kirchhoff面内及横向剪力,对应幅值为

(13)

由于纤维复合材料囊体力学模型求解十分复杂,现引入位移中间向量ξ(φ),位移中间向量由囊体位移量及对应偏导量组成,表达式如下

(14)

依据平衡方程式(11),结合囊体几何方程式(6)与物理方程式(7),即可得到囊体状态向量与位移中间向量的关系式以及位移中间向量的一阶常微分矩阵方程

Z(φ)=Q(φ)ξ(φ)

(15)

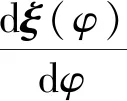
(16)

式中:Q(φ)为八阶关联矩阵;B(φ)为八阶系数矩阵,矩阵中各元素详见附录A。现将囊体切割为N个节点,结合精细积分法[25]即可求解得到位移中间向量在不同节点间的传递关系为

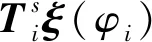
(17)

式中,Ts为位移中间向量间的传递矩阵。将式(15)代入到式(17)中,可得囊体不同节点处状态向量间的传递关系为

(18)

式中,T为囊体状态向量间的传递矩阵。

1.3 囊体刚度特性求解

为求解囊体的全部状态向量,需要明确囊体的边界条件。在气囊隔振器的实际工作过程中,气囊隔振器上安装板连接设备,用于支撑设备质量,并随设备的运动而变形,因此囊体首端为自由边界条件;囊体变形期间,囊体末端始终固定于底座上,因此囊体末端为固定边界条件。假设上安装板随设备的总变形量为,则当囊体发生横向变形时囊体的边界条件为

(19)

依据囊体边界条件式(19),由式(18)可求解得到气囊隔振器囊体各节点处的状态向量。对气囊隔振器囊体首端进行受力分析,得到囊体在变形条件下产生的横向反作用力表达式为

(20)

由于气囊隔振器在变形过程中囊体的状态向量、内部气压以及结构参数之间存在耦合变化关系,现将气囊隔振器的总变形过程分解为n个小变形的叠加,假设气囊隔振器每个小变形过程遵循以下假设:①变形过程中圆弧段囊体始终保持圆弧形;②变形过程中内部气压变化遵从绝热方程;③单个小变形过程中内部气压值P以及结构参数Re和Rφ保持不变。

当气囊隔振器在第个小变形过程中,囊体首端的位移值由yi-1变为yi,依据假设①、②以及③可得到在第个小变形过程中,气囊隔振器结构参数P、Re以及内部气压值Pi的参数表达式为

(21)

式中:Pi-1,Vi-1为气囊隔振器在位移yi-1下的气压值和容积值;Pi,Vi为气囊隔振器在位移yi下的气压值和容积值;ARe、ARφ为横向几何变形系数;ι为热力学多变系数。

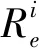
(22)

2 横向刚度特性试验验证

选取8T型、15T型以及30T型气囊隔振器各两个开展横向刚度特性测试。为验证气囊隔振器刚度理论模型的正确性,分别开展空载以及额载工况下气囊隔振器的刚度特性测试。空载工况下气囊隔振器的内部压力为零,额载工况下气囊隔振器的内部压力为额定工作压力,三型气囊隔振器的样机结构参数以及额定工作压力如表1所示,囊体材料参数值如表2所示。

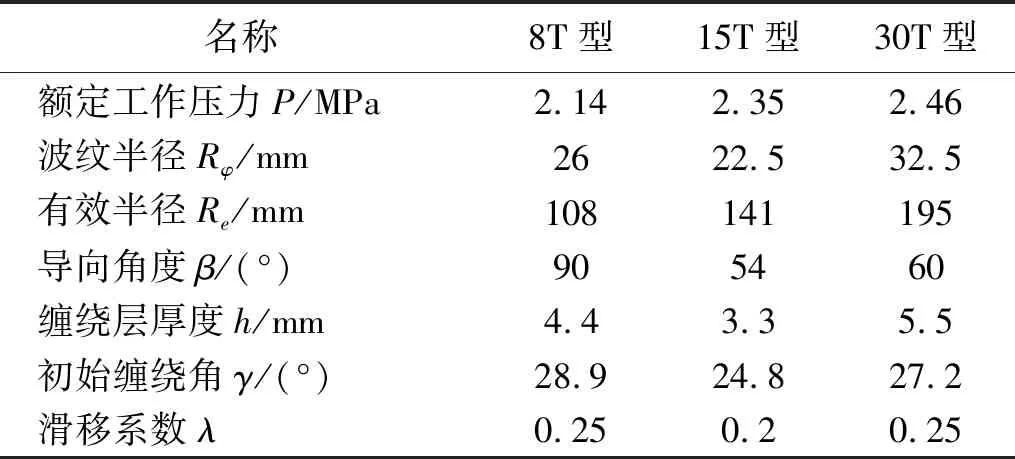
表1 三型气囊隔振器主要设计参数值

表2 囊体材料参数值

参照HJB 590—2014《舰船用气囊隔振器通用规范》开展气囊隔振器横向刚度特性测试试验,测试装置组成及试验情况如图4所示。试验过程中,将两组气囊隔振器以额定高度组合安装至试验机上,待气囊隔振器充气达到指定压力后,以初始平衡状态作为位移原点,按照0.1 mm/s的位移速率,±0.5 mm的位移峰值往复移动试验机上接头(负号表示压缩方向,正号表示拉伸方向),由上接头中的力和位移传感器采集数据并由计算机输出测试值。以15T型气囊隔振器为例,绘制额载工况下气囊隔振器的横向力-位移试验曲线如图5所示,由于橡胶囊体存在黏弹性,因此该曲线存在迟滞效应。为确定气囊隔振器的横向刚度值,一般采用三次多项式对试验曲线进行拟合,再以拟合方程计算得到±0.5 mm位移处的横向力,最终将横向力的变化值作为气囊隔振器的横向刚度试验值。

图4 横向刚度特性测试装置组成及试验情况

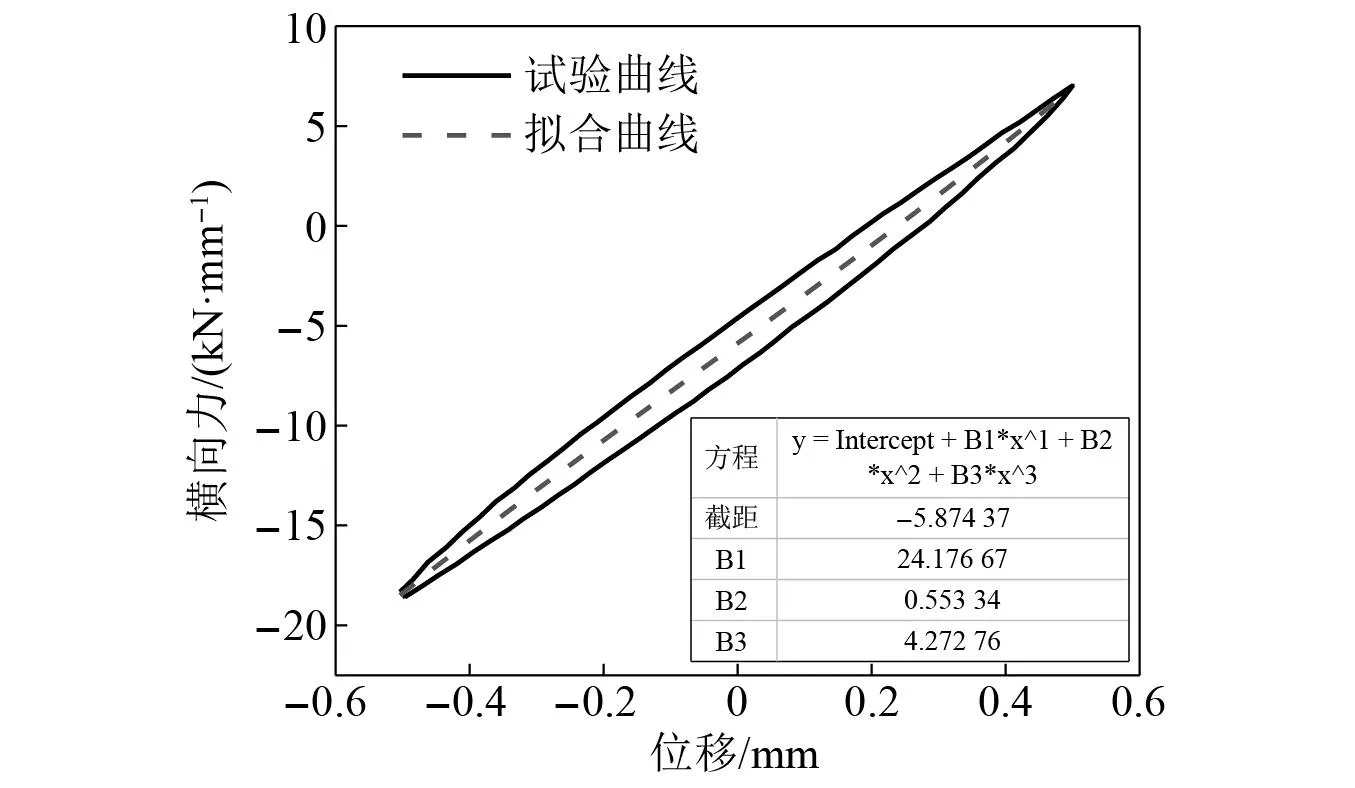
图5 额载工况下15T型气囊隔振器力-位移试验曲线

空载工况下气囊隔振器的内部气压为零,气体刚度理论计算值为零,此时总刚度特性的理论计算值及试验测试值可认为是囊体刚度值,由此验证囊体刚度理论模型的正确性。气囊隔振器横向刚度特性的理论计算结果以及试验结果如表3所示,空载条件下三型气囊隔振器横向刚度特性的理论计算误差均小于10%,可以验证囊体刚度理论计算模型的有效性。

表3 空载条件下横向刚度特性理论计算及试验结果

额载工况下气囊隔振器的内部压力为额定工作压力,此时气体刚度的理论计算值不为零,气囊隔振器横向刚度由气体刚度以及囊体刚度共同组成。额载工况下气囊隔振器横向刚度特性的理论计算结果以及试验结果如表4所示,三型气囊隔振器横向刚度特性的理论计算误差同样小于10%,可以验证气囊隔振器横向刚度特性理论计算模型的正确性。

对表3以及表4中的数据进一步分析可得,在囊体结构大大加强的条件下,舰用气囊隔振器的囊体刚度已明显提高,横向气体刚度已经远低于横向囊体刚度,横向气体刚度在三型气囊隔振器横向总刚度中的最大占比仅为11.4%。因此舰用气囊隔振器的横向刚度值将主要取决于囊体刚度值,基本不受气体刚度的影响。

3 刚度特性影响因素分析

气囊隔振器横向刚度特性的设计参数主要分为三个方面:①几何结构参数,主要为有效半径Rφ,波纹半径Re以及导向角度α;②材料特性参数,主要为纤维复合材料弹性模量E以及纤维缠绕层厚度h;③纤维缠绕参数,纤维缠绕参数为纤维缠绕初始角度γ和滑移系数λ,这两者决定了囊体中各节点处的实际缠绕角度值。

现以15T型气囊为例,通过改变某一设计参数值分析各设计参数对横向刚度特性的影响,为进一步简化刚度特性的分析过程,突出刚度特性的主导影响因素,对气囊刚度特性及其部分设计参数进行归一化处理,归一化处理后的参数表达式为

(23)

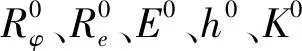
现改变几何结构参数、材料特性参数以及纤维缠绕参数值,计算不同参数下气囊隔振器横向刚度特性,计算结果如图6和图7所示。

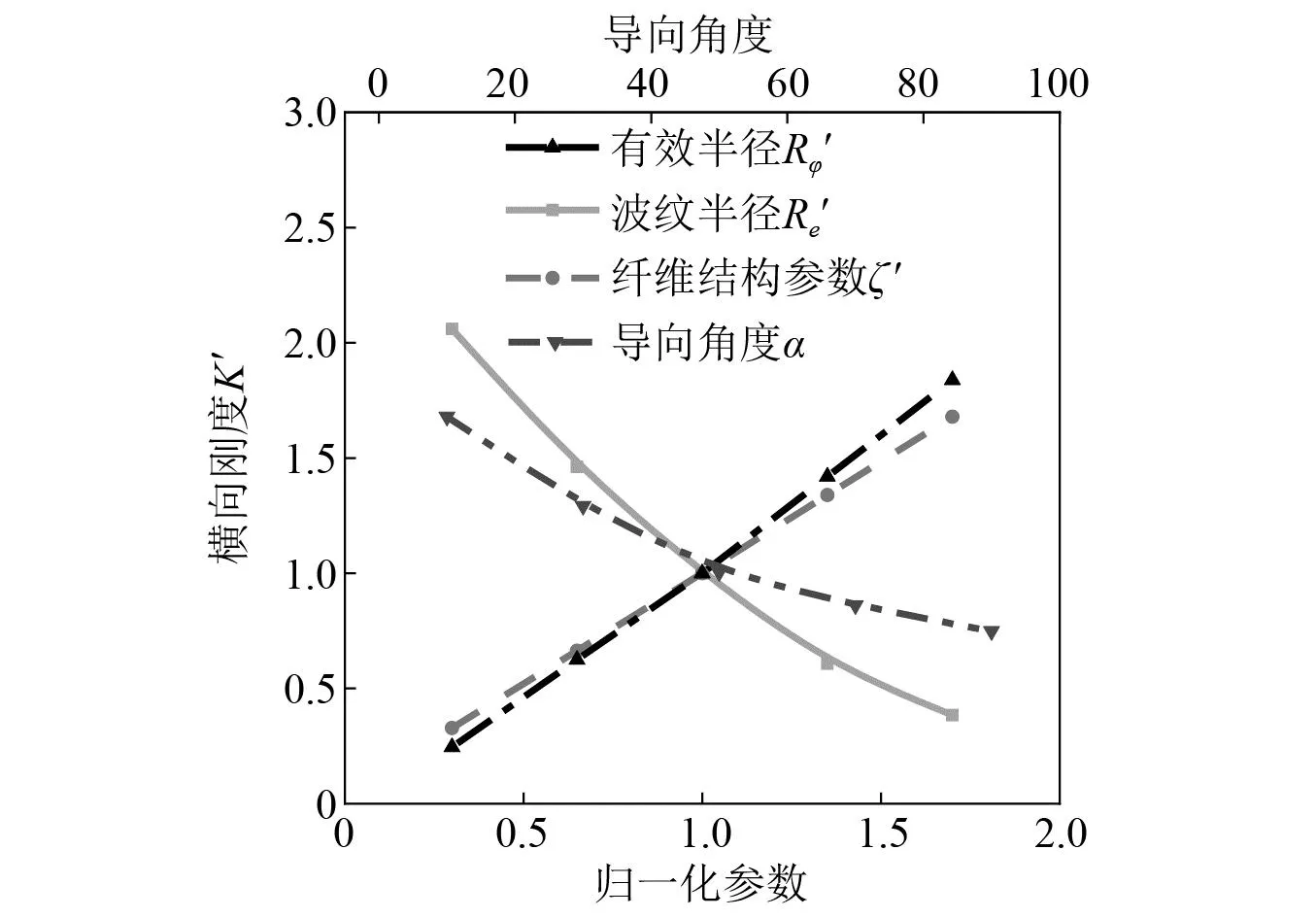
图6 刚度特性随几何结构参数以及材料特性参数的变化曲线图

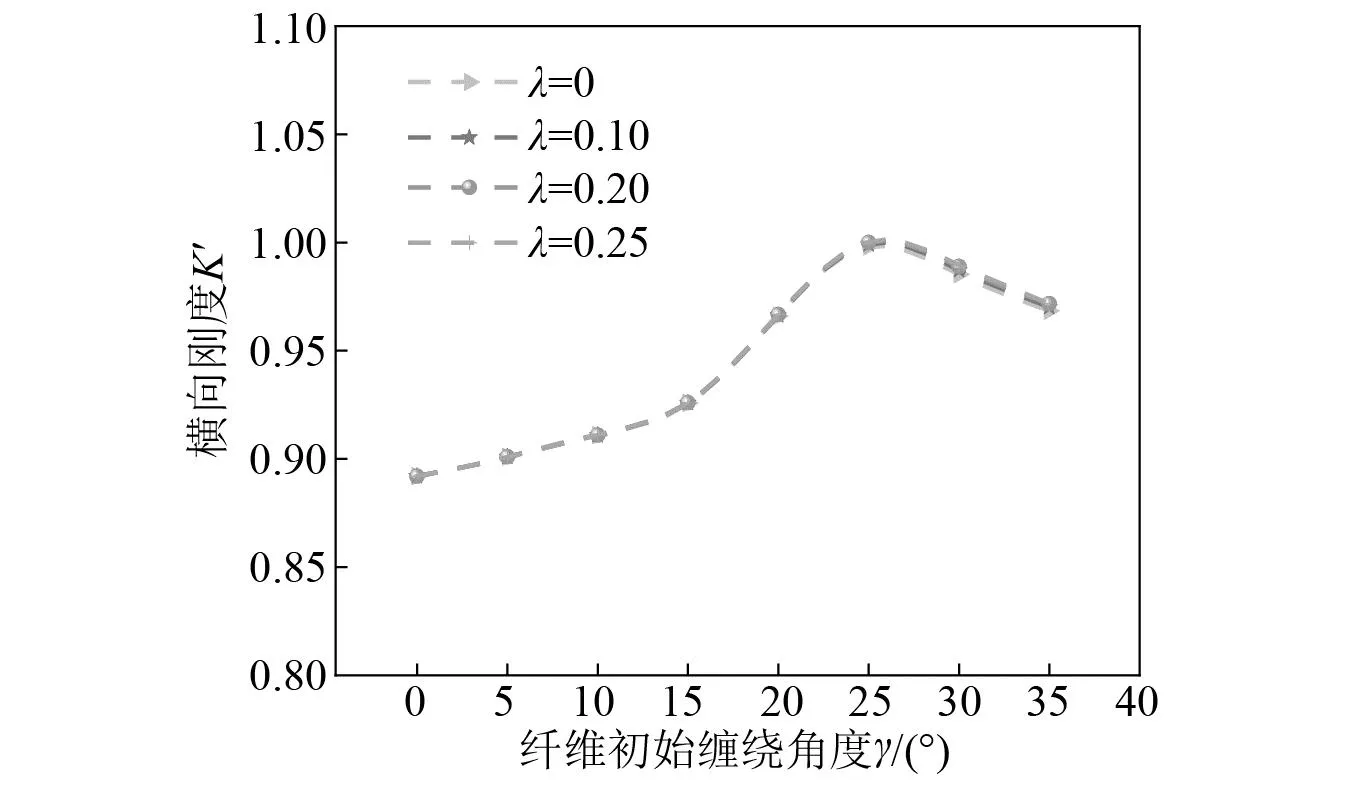
图7 刚度特性随纤维缠绕参数的变化曲线图

由图6可知,几何结构以及材料特性参数对横向刚度特性的影响。在参数变化过程中,气囊隔振器的横向刚度特性随有效半径、纤维结构参数的提高而提高,随波纹半径、导向角度的提高而降低。其中,横向刚度随导向角度以及波纹半径之间的变化关系近似呈二次关系,随纤维结构参数以及有效半径之间的变化关系近似呈线性关系。此外,在整个参数变化区间中,横向刚度特性总变化率从高到低对应的设计参数依次为波纹半径(167.6%)、有效半径(159.3%)、纤维弹性模量同缠绕层厚度(135.1%)、导向角度(93.0%)。刚度特性总变化率反映了各设计参数对刚度特性的影响程度,其中波纹半径对横向刚度的影响作用最强,导向角度对横向刚度的影响作用最小。

由图7可知,纤维缠绕参数对横向刚度特性的影响。纤维缠绕参数中滑移系数对横向刚度基本无影响,纤维初始缠绕角度对横向刚度特性有一定影响:随着初始缠绕角度的增加,横向刚度值先提高后降低,存在最大值,当初始缠绕角度约25°时,横向刚度值接近最大值。从整体上来看,在纤维缠绕参数变化的整个过程中,横向刚度值最大变化仅占变化初值的11.2%,对比图6,纤维缠绕参数对刚度特性的影响要远小于几何结构参数以及材料特性参数对刚度特性的影响。

4 结 论

(1) 构建了预载条件下的气囊隔振器的囊体力学模型,并基于精细传递矩阵法以及迭代法求解了囊体横向刚度,结合理想气体刚度模型完成了气囊隔振器的横向刚度特性计算。经试验测试,空载以及额载工况下三型气囊隔振器的横向刚度特性理论计算误差均小于10%,验证了横向刚度特性计算方法的有效性。

(2) 气囊隔振器的横向刚度随有效半径、材料结构参数的提高而提高,随波纹半径、导向角度的提高而降低。其中,横向刚度随导向角度以及波纹半径之间的变化关系近似呈二次关系,随纤维结构参数以及有效半径之间的变化关系近似呈线性关系。

(3) 纤维缠绕参数对刚度特性的影响远小于几何结构参数以及材料特性参数对刚度特性的影响,基本可忽略。几何结构参数以及材料特性参数中的波纹半径、有效半径、纤维弹性模量同缠绕层厚度以及导向角度对横向刚度的影响作用依次降低。

附录A

关联矩阵Q(φ)中的元素

系数矩阵B(φ)中的元素