列车荷载作用下压实花岗岩残积土累积变形特性试验研究
尹 松, 刘鹏飞, 孙玉周, 李新明, 闫 盼, 王志留
(1. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室,武汉 430071;2. 中原工学院 建筑工程学院,郑州 450007)
花岗岩残积土属区域性特殊土,广泛分布于我国东南部省份[1]。随着华南地区基础设施的不断完善和交通运输行业的迅猛发展,花岗岩残积土富集带路基填筑工程量巨大[2]。该类土虽具有较优的力学特性,但因液塑限高、孔隙比大,且遇水易湿化崩解[3-4],工程应用往往受限。压实花岗岩残积土工程载体易受环境气候条件影响,其作为路用材料工程应用时,需重点关注其变形特性及稳定性[5]。结合压实花岗岩残积土的荷载形式、应力状态及物理条件,研究多条件耦合下压实花岗岩残积土在列车循环振动作用下的变形特性,对于深入认识花岗岩残积土的动力特性及其工程敏感性具有重要意义。
在过去,动三轴被广泛用于研究循环荷载作用下土的长期永久变形。研究内容包括永久应变随振动循环次数的发展规律、永久变形与微观结构的联系、不同振动条件对土体应变累积特性的影响等方面[6-7]。残积土因其非均质性和区域差异性,难以对不同地域残积土的动力变形特性一概而论[8]。因此,研究者开始通过进行类似的动三轴试验,探究花岗岩残积土的累积塑性变形特性。祝方才等[9]研究发现在吸力一定的情况下,衡阳非饱和花岗岩残积土的动应力应变骨干曲线呈双曲线型,且随着净围压增大向上移动;刘新宇等[10-11]评价了振幅和频率对残积土的动力损伤和变形影响;陈志波等通过动三轴试验研究了振次对福州原状花岗岩残积土动应变的影响,并将其应变曲线分为三种典型类型。证实了花岗岩残积土的动力特征与软黏土、红黏土等类别土具有一定的相似规律,但其外部加载条件差异所导致的变形特性存在差异,对其动力特性研究应结合堆填物的赋存条件进行针对性分析。
但值得商榷的是,由于设备局限性,动三轴设备不能模拟主应力轴旋转效应。众所周知,路基土体单元应力分量大小和方向会随着列车荷载的作用时间而不断变化[12-13],导致作用在土单元体上的主应力轴连续旋转,从而形成“心型”应力路径[14-15]。而主应力轴旋转效应会加剧土体的永久累积变形[16-17]。以动三轴设备模拟列车荷载必然会导致残积土的累积塑性应变偏低,影响工程安全,这一点在相关研究文献中也得到了报道[18-20]。因此,有必要使用更高级的空心圆柱扭剪系统来模拟实际列车荷载引起的花岗岩残积土体的复杂应力变化。
综上所述,本文借助GCTS空心圆柱扭剪试验设备实现了心型应力加载路径,最大程度模拟了列车荷载的作用形式。结合花岗岩残积土分布地区的多雨气候特点,研究了列车荷载形式作用下围压、含水率、加载幅值以及应力路径等因素对压实花岗岩残积土累积变形特性的影响,应用理论数学模型对累积变形进行预测,并对模型的适用性进行验证和扩展。研究可为该类土体工程应用提供技术支持。
1 土样性质和试验方法
1.1 土样性质
取样场地位于广东省台山市,参考TB 10102—2023《铁路工程土工试验规程》[21],对台山花岗岩残积土进行基本物性试验,详细指标如表1和图1所示。由表1和图1可知,该类土自由膨胀率较小,天然含水率和液塑限较高;最优含水率w=19.5%,最大干密度ρ=1.70 g/cm3。土体类别属含砂高液限黏土。残积土颗粒分布存在间断级配现象,不均匀系数Cu>10,曲率系数Cc<1。土样主要成分为黏土矿物(高岭石)和石英,含少量黄铁矿。
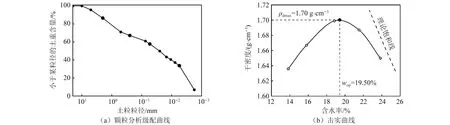
图1 花岗岩残积土颗粒级配和击实曲线

表1 花岗岩残积土的物理特性指标
1.2 试验仪器
试验仪器为GCTS-动态空心圆柱扭剪仪。相较传统动三轴设备,其可以施加独立变化的内、外围压、反压以及轴向、扭剪循环动荷载;可以设置多种加载波形,如正弦波、矩形波以及自定义波形,能够模拟交通、海浪等复杂的应力路径,体现主应力轴旋转效应。
1.3 制样方法与应力条件
重塑试样尺寸为200 mm×100 mm×50 mm(50 mm为内径),该尺寸可使试样端部约束导致的应力不均匀性处于可控水平[22];为贴近工程实际,试样以最优含水率为基准,并设置过干或过湿含水率以模拟极端状况。不同含水率试样的制样方法参考文献[18],试样的平均应力状态和应力水平如图2所示[23]。
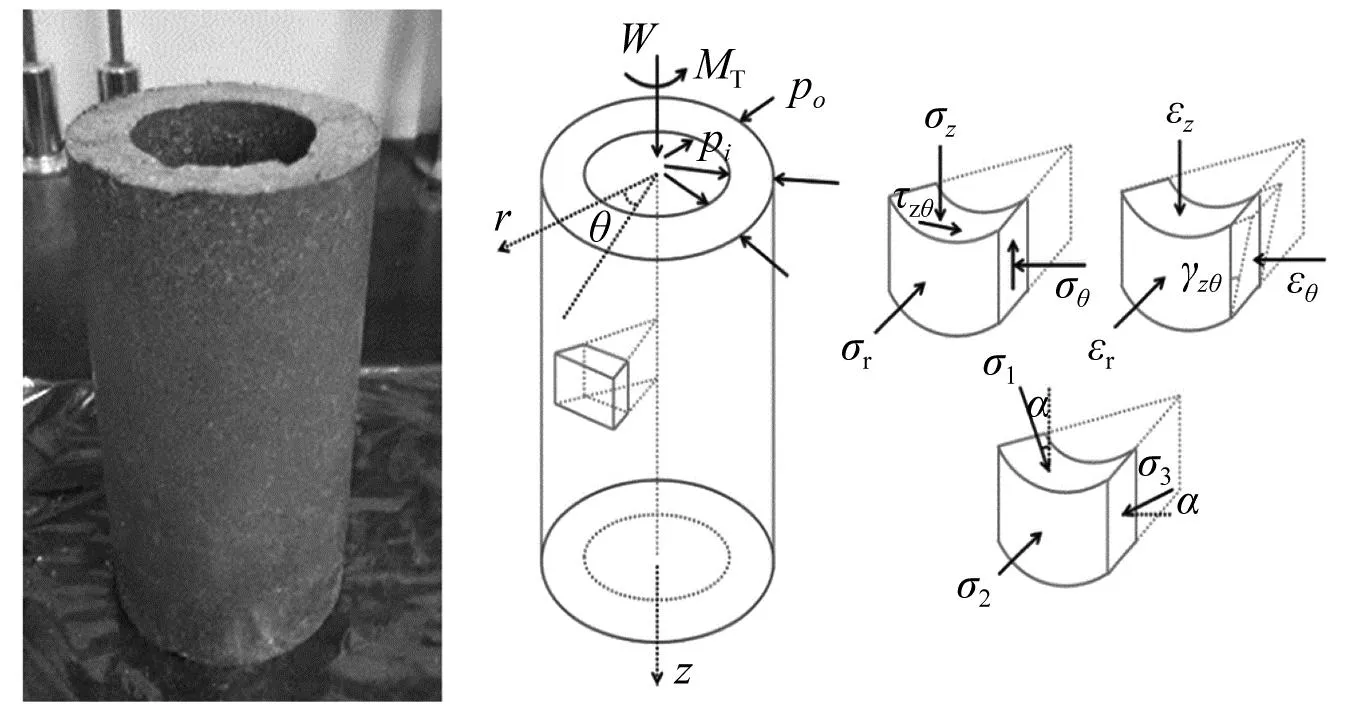
图2 空心试样及其应力应变状态
1.4 试验方法
为模拟工程中铁路路基的真实排水条件,获得路基土体最大可能变形,试验在排水排气条件下进行[24]。分别对不同含水率试样在30 kPa、50 kPa、100 kPa三种围压下进行稳压固结,稳压固结期间内外围压保持恒定,其中饱和试样应先在设备上完成饱和再固结。
待试样变形稳定或固结完成后(<0.01 mm/min)进行循环扭剪试验,考虑路基实际服役状态,设定累积应变超过5%时试验停止。循环三轴试验作为对比试验,除未设置主应力旋转外(未设置剪应力),其他参数均与循环扭剪试验相同。
通过现场传感器实测动应力和有限元模拟,并考虑列车荷载影响深度、路基基床形式以及车速等因素影响[25-26],本文设置如表2所示的扭剪动应力荷载组合以模拟“心型”应力路径。加载频率f根据实际列车时速200 km/h计算取为2 Hz,具体加载波形和动应力荷载组合方案如图3和表2所示。
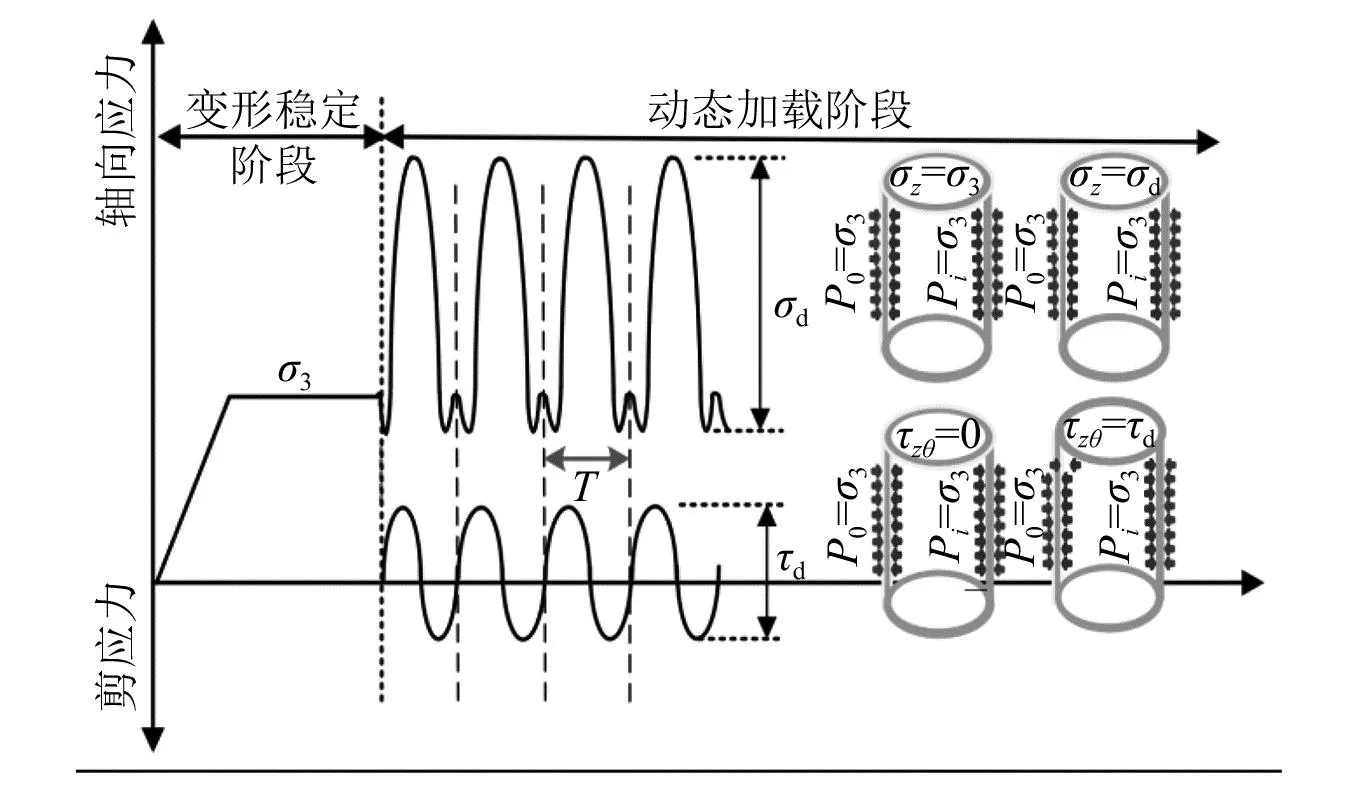
图3 加载波形

表2 路基土体单元动应力组合
2 试验结果与分析
正式进行动力加载试验前对输出波形进行检验,确保其与输入波形一致。输出时程曲线及心型应力路径如图4所示。可见,输出时程曲线的σzd和τdzθ值均与设计值相符。输出的应力路径与设计应力路径虽有偏差,但整体处于可控范围。表明通过空心扭剪仪双向振动实现“心型”应力路径是切实可行的,能够模拟列车荷载下路基土体实际应力状态。
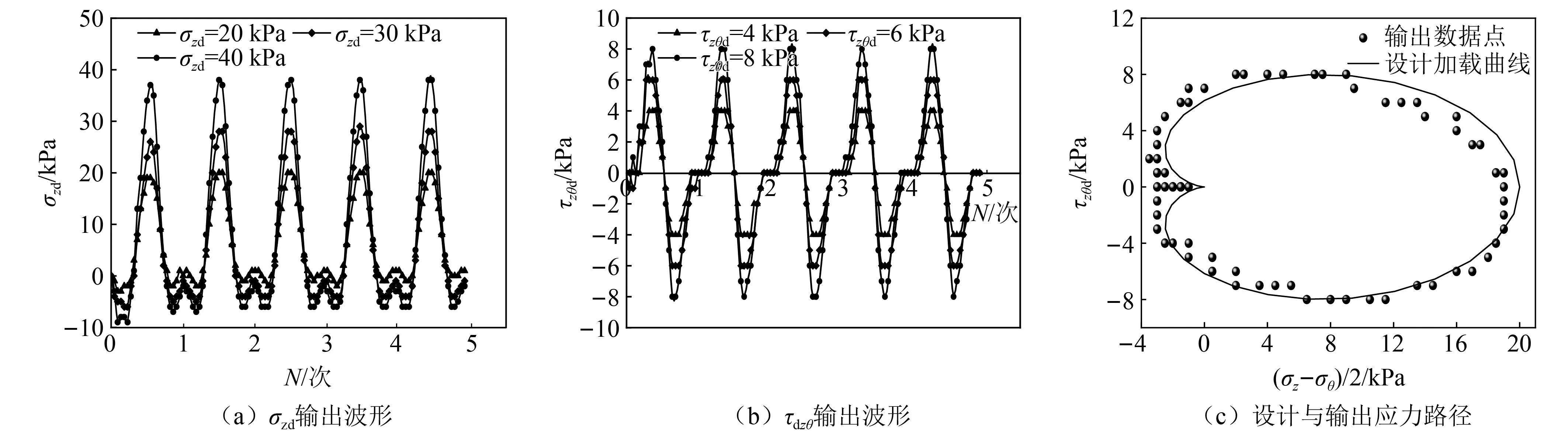
图4 输出时程曲线及心型应力路径
2.1 动应力应变关系
选取典型动力加载条件下(σc=30 kPa,σzd=30 kPa)试样滞回曲线进行分析,如图5所示。由图5可知,滞回曲线表现出明显滞后性和应变累积性。随着循环加载次数增加,滞回曲线之间的距离和包围面积逐渐减小,曲线中轴线斜率逐渐变大,表明加载过程中花岗岩残积土的塑性应变逐步减小,刚度逐渐增大。
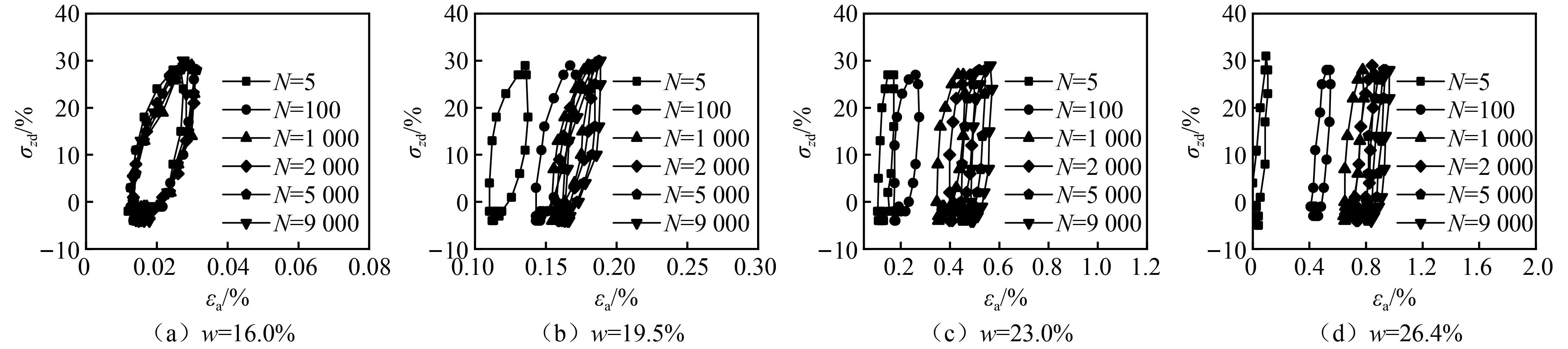
图5 循环扭剪条件下土体动应力应变关系
此外,由于残积土的水敏性,含水率对土样应力应变关系影响较大。低含水率试样(w=16.0%)的滞回曲线随N的增加并未发生明显的变化;初始含水率试样(w=19.5%)的滞回曲线在N>100后接近重合,2 000次循环加载后滞回曲线集中堆积,表明土样的应变发展趋于稳定。随着试样含水率达到23.0%和饱和状态时,滞回曲线在N<2 000时不断向右移动,塑性应变发展较快,且在N>2 000后仍在持续右移并逐渐堆积,发展趋势不易稳定。
2.2 围压对累积变形特性的影响
由于w=16.0%~26.4%含水率条件下,不同轴向应力幅值试样累积塑性应变随围压的发展规律较为相近,选取σzd=30 kPa时不同围压下土体累积塑性应变随荷载作用次数的发展规律进行分析,如图6所示。
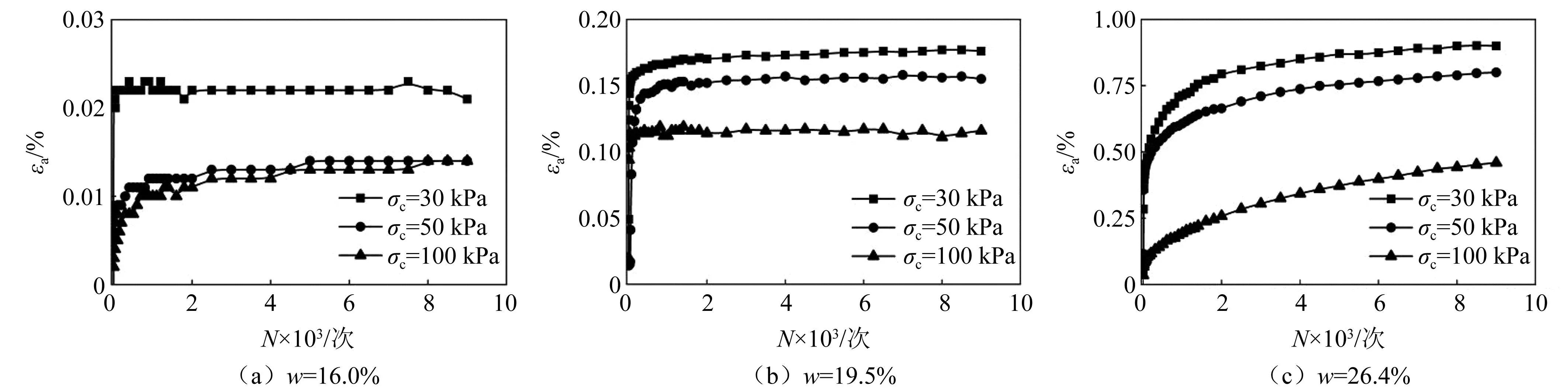
图6 不同围压下的累积塑性应变
对比发现,随着围压的增大,试样累积塑性应变值εa呈减小趋势,前期应变发展随围压的增大不断减慢,且达到相对稳定状态所对应的N值增大。此外,围压的影响程度随含水率的增加越发明显,例如w=19.5%时,试样在50 kPa和100 kPa围压下的极限累积应变差值仅为0.03%,w=26.4%时,两种围压下的极限累积应变差值可达0.40%,且尚未出现稳态发展。这主要是含水率的增加导致土体颗粒间水膜增厚,粒间黏聚力降低,润滑作用增强,围压的改变对颗粒间的嵌挤作用影响明显所致。
2.3 加载幅值对累积变形特性的影响
选取围压σc=50 kPa条件下,含水率分别为w=19.5%、23.0%条件下的试验数据,分析动应力幅值对试样累积应变特性的影响,如图7所示。
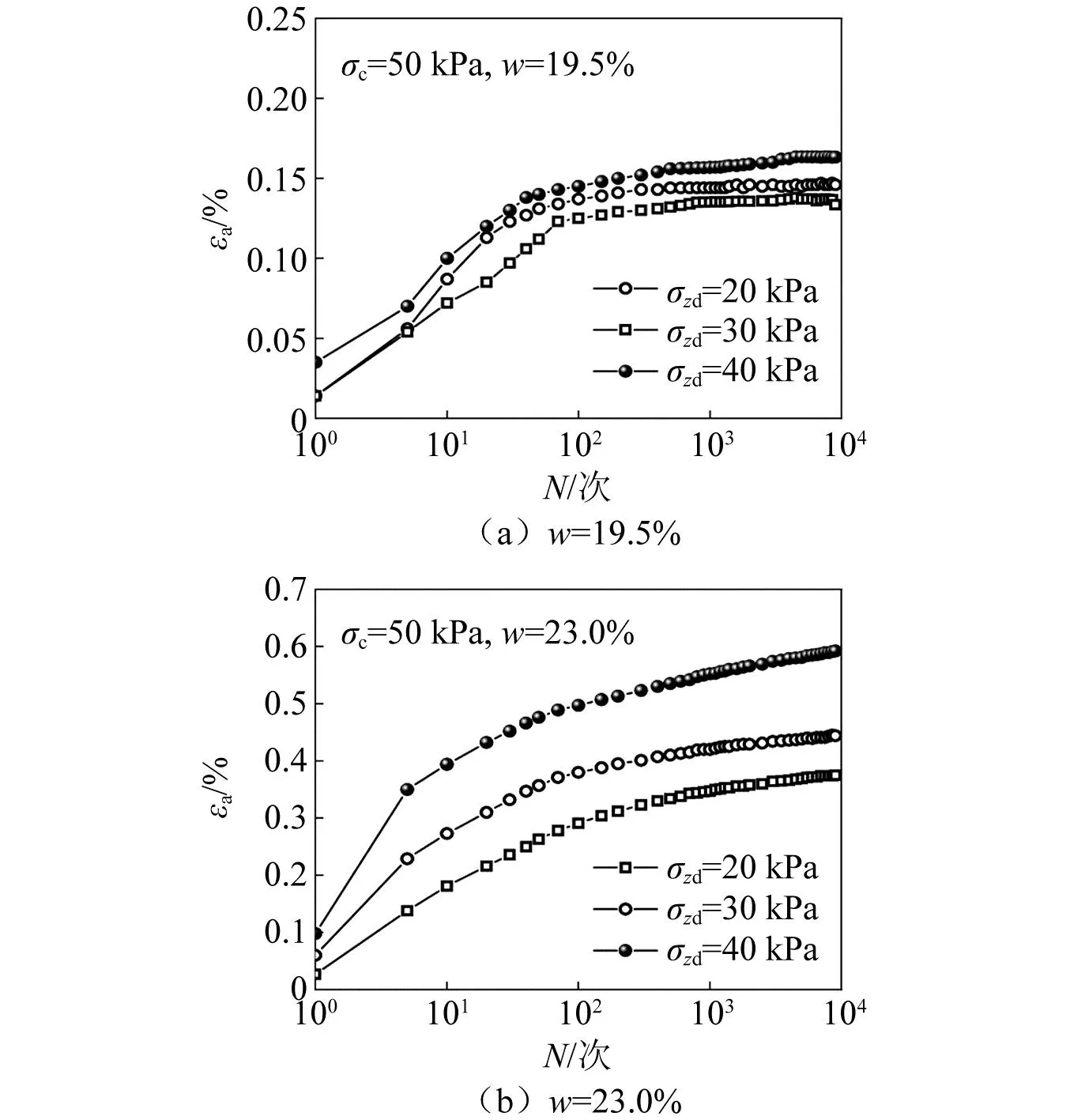
图7 不同动应力幅值下土体累积塑性应变
由图7可知,经过相同循环加载次数的试样,动应力幅值越大,其累积应变越大。应力幅值不同,累积应变随荷载作用次数的发展速度也不同。随着加载次数的增加,应变发展速率由于应力幅值的不同,存在不同程度的减缓。
另外对比图7(a)、图7(b)发现,残积土的水敏性导致应力幅值对不同含水率下试样变形影响差异较大。w=19.5%时,随应力幅值增大,累积应变增幅相对较小且随作用次数增加迅速趋于稳定;w=23.0%时,应变随应力幅值增大而增幅明显,随作用次数增加,应变仍有缓慢发展趋势。
2.4 含水率对累积变形特性的影响
残积土多分布于热带及亚热带地区,受风化作用影响,土中矿物成分复杂,水敏性较强。其作为路基填料进行工程应用时需着重注意多雨环境影响。图8给出了σc=50 kPa条件下不同含水率下试样的累积塑性应变发展曲线。

图8 不同含水率土样累积塑性应变及应变稳定值
分析可知,不同轴向加载幅值条件下,εa随含水率增加逐渐增大。含水率过高将导致土体累积塑性应变发展趋势改变,难以达到稳定状态。
σzd=20~40 kPa,τzθ=4~8 kPa条件下,低含水率试样(w=16.0%)在N<100时便已趋于稳定,εa值不超过0.02%,初始含水率(w=19.5%)试样的εa值同样较小,N<1 000时趋于稳定,εa<0.20%。试样增湿至w=23.0%时,累积应变增幅较w=19.5%高达2倍以上。试样增湿至饱和状态时,应变发展趋势已完全不同于前三者,εa值随N的增大不断增大,应变发展趋势由稳定型转化为指数发展型,且加载幅值越大,该趋势越明显。分析认为,这主要是因为加载频率较高导致试样孔隙水无法充分排出,土体空隙内产生一定动水压力,使得土体颗粒组成被破坏,减弱了土体抗变形能力,该压力越大,破坏效应越明显,这也与路基实际工作状态中的加载及排水条件相似。所以路基填筑应充分考虑车辆荷载和水环境耦合作用下材料的水稳性能及变形特性,注意增设防排水设施,保持路基良好的运营状态。
2.5 应力路径对累积变形特性的影响
图9给出了σzd=20 kPa、40 kPa,σzd=50 kPa,w=19.5%及w=26.4%时,三轴及循环扭剪动力加载路径下试样的累积塑性应变发展规律。
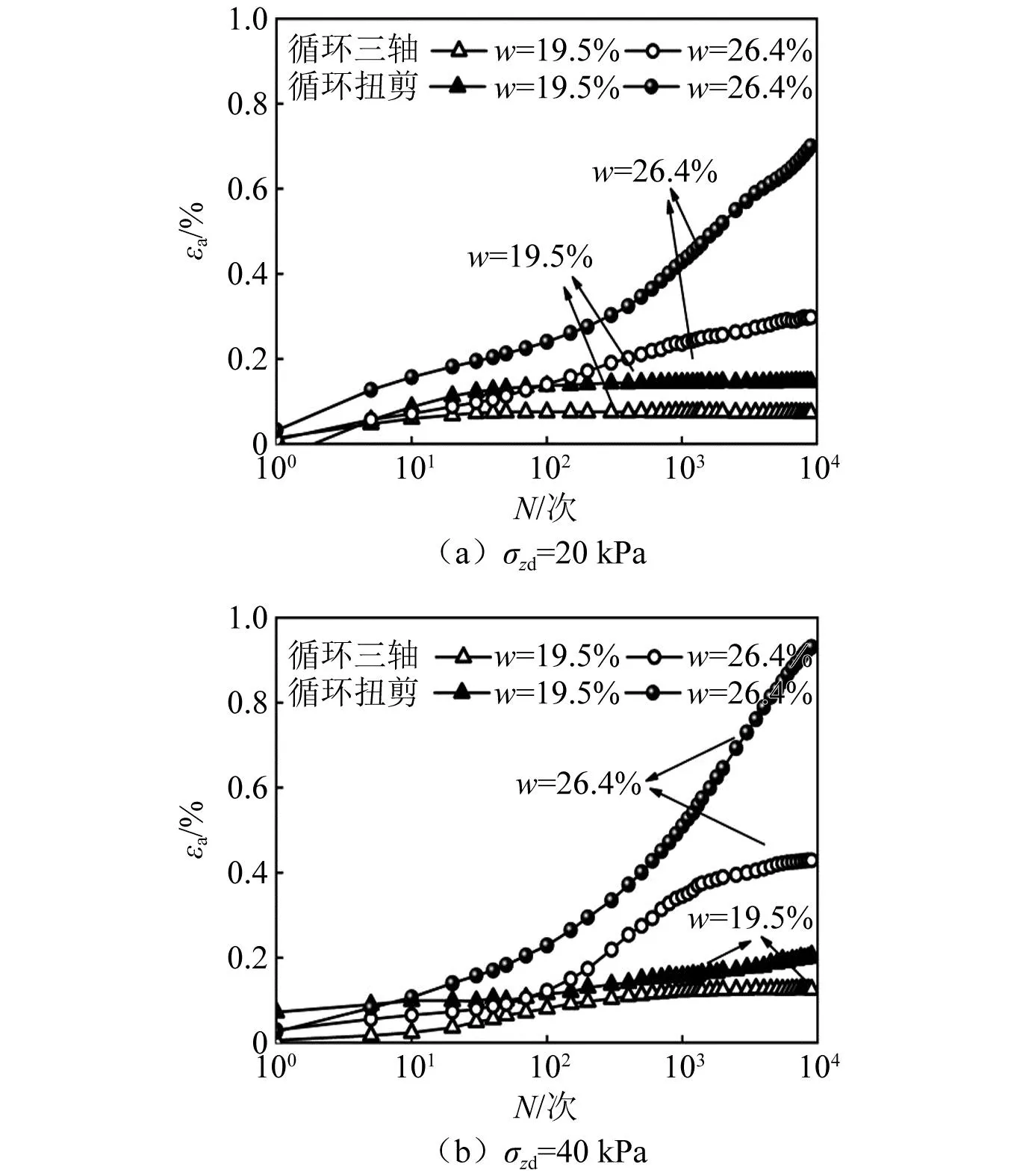
图9 各应力路径下土体累积塑性应变
由图9可知,相同围压、含水率及竖向动应力加载幅值下,两种应力路径试样的累积塑性应变发展规律存在一定差异。“心型”应力路径加载条件下主应力轴旋转效应增加了试样的应变的累积量,甚至改变了累积应变的发展模式。
w=19.5%试样在两种加载路径下应变发展趋势相似,应变差值不超过0.05%且最终均趋于稳定。而随试样含水率增高至w=26.4%时,“心型”应力路径下试样累积应变发展趋势不同于三轴定向动力加载应力路径下的试样累积应变发展规律,其εa值大幅增长,“心型”应力路径下试样累积应变最高可达到定向剪切路径试验结果的2倍以上,且不再存在稳定值,演化为发展型规律曲线。这主要是因为“心型”动力加载应力路径应变增量存在非共轴特性,随着主应力轴的旋转,应力不断被加载、卸载,但塑性应变却在循环加载中逐渐累积,无法完全恢复。此外,当含水率升高,主应力轴连续旋转也会引起孔压升高,试样内部颗粒排列方式被破坏,且程度加剧。所以扭剪耦合动力加载易加剧试样的累积变形发展程度,工程设计及其实验室模拟试验中应予以注意。
2.6 累积塑性应变发展速率变化规律
通过单位振次累积塑性应变表征累积应变发展速率,分析围压、动应力幅值和含水率对应变发展速率的影响,如图10所示。
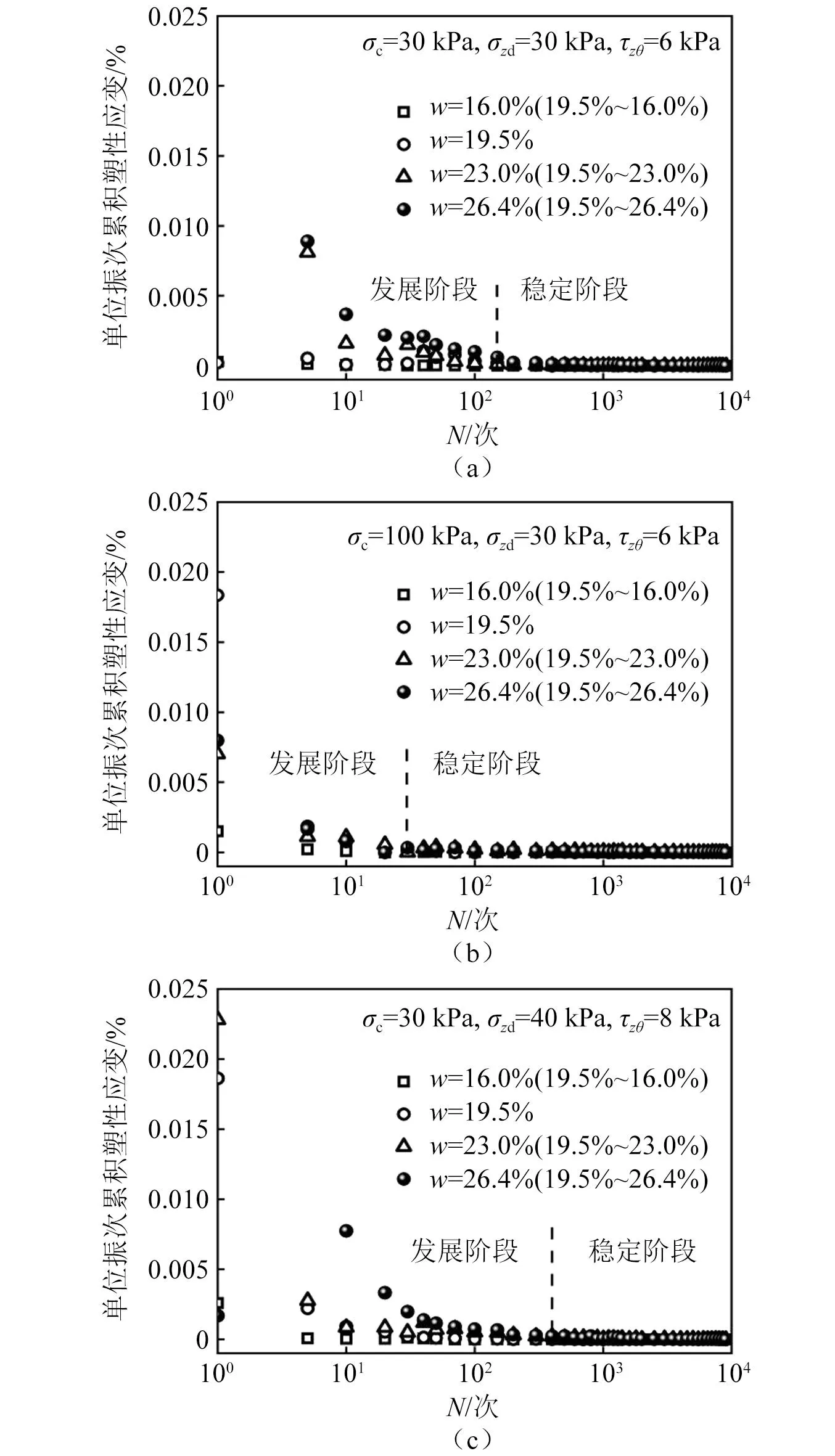
图10 累积塑性应变发展速率变化规律
分析认为,整体上压实花岗岩残积土的累积应变发展速率vεa呈加速度不断衰减的模式,N<100时已完成大幅度衰减,表明土体塑性应变已完成大量累积。围压增大可加快累积应变发展速率vεa的衰减,例如σzd=30 kPa,σc=30 kPa时,试样的vεa在循环加载次数N为170时达到稳定,围压增加至100 kPa时,各含水率试样的应变发展速率在N<20时便完成大幅衰减。反映了相同条件下,深埋土体的变形更加易于稳定。
此外,动应力幅值的增加会延长累积应变发展速率的衰减时间,例如σc=30 kPa条件下,当σzd从30 kPa增加至40 kPa,土体达到稳定状态的循环次数N从170次延后到400次,即轴向动应力幅值越大土体变形更难达到稳定状态。高含水率试样的累积应变发展速率衰减程度明显大于低含水率试样,其土体变形更难达到稳定状态。
图11给出了含水率w=19.5%和w=26.4%的试样在不同动力加载应力路径条件下(循环扭剪和循环三轴),单位振次累积塑性应变与循环次数的双对数关系。对比试样的累积应变发展速率vεa可发现,相同循环加载次数下,循环扭剪试验的累积应变发展速率vεa衰减程度小于循环三轴定向加载试验。随循环次数增加,应变发展速率vεa差异更为明显且含水率越高该规律越明显,进一步说明了动力加载应力路径对于含水率较高的土体的应变发展速率影响较大,应予以重视。通过循环三轴定向加载试验得到的累积变形值和变形速率衰减值过于冒险,对于列车振动所引起的累积塑性变形应充分考虑应力路径及土体物理状态造成的影响。
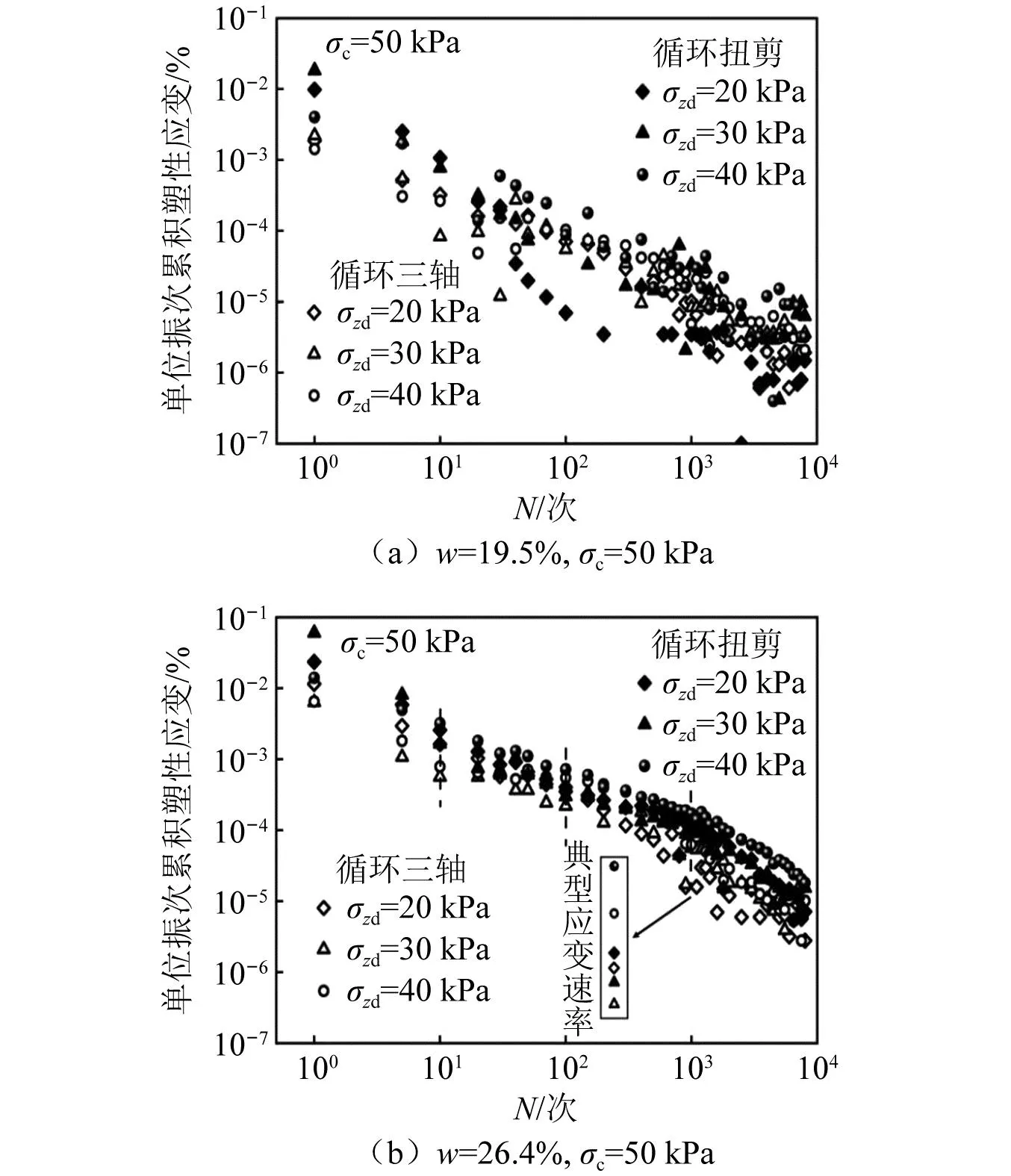
图11 累积塑性应变发展速率变化规律
3 累积应变预测分析
由第2章分析结果可知,通过循环扭剪和循环三轴定向加载试验得到的试样累积塑性应变发展曲线形态可归纳为稳定型和发展型两种。而目前的累积塑性应变预测多为稳定性和发展型单一形态累积应变发展预测。所以本文对张勇[27]所提出的稳定型累积应变预测模型参数进行分类调控,如式(1)所示
(1)
若累积应变发展曲线为稳定型,γ>0。其中N为循环作用次数,α、β、γ为与土的性质和应力条件相关的参数。α代表应变达到稳态的速度;β的大小与含水率成反比;γ反映了应变发展曲线的形态。若累积应变发展曲线为发展型,即γ<0,此时设γ=0,模型可演变为发展型曲线的预测模型,其中,α反映应变曲线发展的速度;β的大小与试样物理状态相关。以围压σc=100 kPa时不同含水率的花岗岩残积土的累积应变发展规律为例进行拟合。拟合结果和参数如图12和表3所示。

图12 累积塑性应变拟合曲线
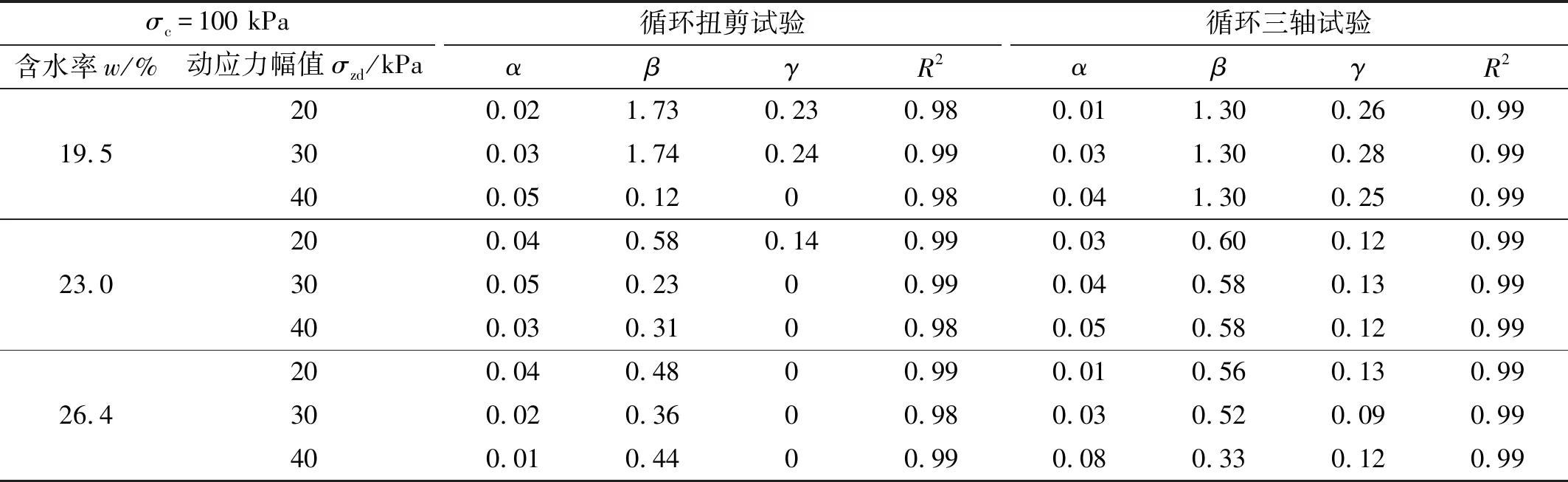
表3 模型拟合参数
由图12和表3可知,模型能够较好地拟合循环扭剪和三轴试验结果,相关系数较高,具有良好适用性。其用于预测列车荷载作用下土体累积应变随加载次数的发展规律效果较好。
分析发现,循环三轴加载试验中,残积土试样的累积塑性应变发展曲线全部为稳定型发展趋势;而循环扭剪加载的试样中,部分试样随着含水率的升高,动应力幅值较高的试样累积塑性应变由稳定型向发展型转化,饱和试样累积塑性应变发展曲线全部为发展型。
分析拟合参数发现,稳定性发展曲线中(γ>0),α值代表应变达到稳态的速度,α值越小,应变越早达到稳态。不同加载条件,α值差异明显,整体而言,相比于循环三轴定向加载条件,循环扭剪加载条件下的α值较高,试样含水率和β值呈反比,含水率越高,β值越小,相对应的εa值越大;对于发展型曲线(γ=0),α值则反映了曲线发展的速度,α值越小,应变发展越快,越难以稳定,整体而言,相比于循环三轴定向加载条件,循环扭剪加载条件下的α值较小;β值随含水率的升高而增大,说明εa迅速增加并产生破坏。
整体而言,该预测函数能够考虑列车循环振动作用下花岗岩残积土塑性变形的类型,可对土体的长期累积塑性应变进行预测。
4 结 论
(1) 残积土的滞回曲线在加载过程中呈现明显滞后性和应变累积性。高含水率试样变形难达到稳定状态。围压对于高含水率试样的累积塑性应变发展具有明显抑制作用。
(2) 残积土的水敏性导致应力幅值对不同含水率下试样变形影响差异较大。随着试样含水率的增大,累积应变随应力幅值增大而增幅明显。高含水率土体的累积应变发展难以达到稳定状态。路基施工和维护应注意控制含水率变化。
(3) 相同竖向加载应力条件下,心型应力路径下的主应力轴旋转效应增加了试样的应变累积量,甚至改变了高含水率试样累积应变的发展模式。作为铁路路基土应充分考虑主应力轴旋转产生的影响。
花岗岩残积土的累积应变发展速率在N<100时已完成大幅度衰减,高围压有利于发展速率衰减,动应力幅值增加会延长发展速率的衰减时间。心型应力路径下试样的累积应变发展速率显著高于循环三轴定向加载路径。
累积应变预测模型可较好地对两种应力路径下稳定型和发展型的累积应变曲线进行拟合和预测。拟合参数能够反映加载条件、物理状态等因素对于土体变形特性的影响。

