智能约束层阻尼结构动力学建模及振动主动控制研究

黄志诚, 黄 帆, 王兴国, 褚福磊

(1. 景德镇陶瓷大学 机电学院,江西 景德镇 333403;2. 清华大学 机械工程系,北京 100084)

近年来,智能约束层阻尼(intelligent constrained layer damped,ICLD)结构是在传统被动约束层阻尼基础上结合压电材料的机电转换特性以及控制理论发展起来的。部分覆盖压电层和黏弹性层ICLD悬臂梁结构如图1所示。结构发生振动时,压电传感层自动拾取结构振动信号并通过反馈控制使压电约束层发生相应形变以主动调节黏弹性材料的剪切变形,实现结构振动的智能控制[1-5]。ICLD因结构简单,附加质量低、可控频带宽、控制效果好等优点,广泛应用于车辆、航空航天等领域[6-8]。

传统被动约束层阻尼通过加剧黏弹性材料剪切变形的方式增加振动能量的耗散以达到抑制结构振动的目的。Baz等[9]、Lesieutre等[10]、Shi等[11]分别使用不同物理模型表征黏弹性材料阻尼特性。王攀等[12]的研究表明:被动约束层阻尼仅对结构的高频振动有较好抑制效果,但对结构低频振动的控制效果不理想。之后,学者陆续投入到对结构低频振动控制效果较好的主动约束层阻尼技术研究中,Swigert等[13]最先将压电材料引入到振动控制系统中,率先实现了结构振动主动控制。众多学者的研究证明:主动约束层阻尼能够在较宽频率范围内抑制结构的振动,但是目前主动约束层阻尼结构的建模方法会引起结构模型的自由度过高,不利于后续结构控制器的设计。因此结构模型需要降阶处理,一方面物理空间模型降阶方法虽然能保留结构模型所有的物理信息,但是在物理空间降阶后的结构模型自由度仍然过高且该方法并不能改变结构模型的可控制性和可观测性[14-15];另一方面,状态空间降阶方法虽然能改变结构模型的可控制性和可观测性,但是结构模型的物理意义不明确。联合降阶是目前处理高维系统的主要手段[16],即先将高维ICLD结构在物理空间降阶,然后在状态空间进行降阶处理,此方法既可以保留高维模型的低阶物理信息,又可以改变系统的控制性和观测性。

基于以上问题,本文提出不同的ICLD结构建模策略,即先采用有限元法对ICLD悬臂梁结构划分的单元进行组集,然后再结合描述黏弹性材料阻尼特性的GHM模型推导出ICLD悬臂梁结构的动力学模型,此方法可以在保证结构模型正确的基础上初步降低系统自由度。其次对高维系统进行联合降阶,即先在物理空间缩聚结构模型的物理自由度,然后在状态空间构造相应的模态空间,实现ICLD结构非比例阻尼的解耦和模态截断工作。然后,比较分析压电片铺设位置对ICLD结构振动控制效果和控制成本的影响。最后,以含有噪声的激励信号为输入再次验证简化结构模型的普遍适用性。基于以上几点得到了一些对悬臂梁振动控制研究有一定借鉴意义的结论。

1 有限元法建模

1.1 压电材料特性分析

压电材料因其同时具有弹性体和介电体的双重属性,所以压电材料既具有弹性特征还具有压电特征。当压电材料表面受到外力作用时,压电材料两端因外力作用而产生电位差的现象称为正向压电效应,因此压电材料可以作为传感器使用;当压电材料两端受到电压作用时,压电材料因电压作用而产生形变的现象称为逆向压电效应,因此压电材料也可以作为作动器使用。

压电材料在外力和电场作用下的压电方程为[17]

(1)

式中: 方程分别为压电材料的逆向压电效应和正向压电效应;ε,σ,D,E,d分别为应变、应力、电位移、电场和压电应变常数。

1.2 基本假设

图1中:①为基梁和压电层均满足Euler-Bernoulli梁理论; ②为基梁、黏弹性层和压电层有相同的横向位移;③为各层转动惯量的影响忽略不计;④为仅考虑黏弹性层剪切变形提供的结构阻尼;⑤为各层之间是理想粘贴,层间无相对滑动;⑥为各层均符合线性理论。

1.3 单元运动耦合关系

ICLD悬臂梁变形前后的位移关系图,如图2所示。

图2 ICLD悬臂梁变形位移关系

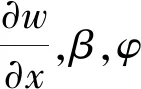
结合ICLD悬臂梁几何变形关系以及一阶剪切变形原理[18],推导出压电传感层、黏弹性层x方向位移和黏弹性层剪切应变的表达式为

(2)

(3)

(4)

在前述假设基础上建立的ICLD梁单元模型,如图3所示。

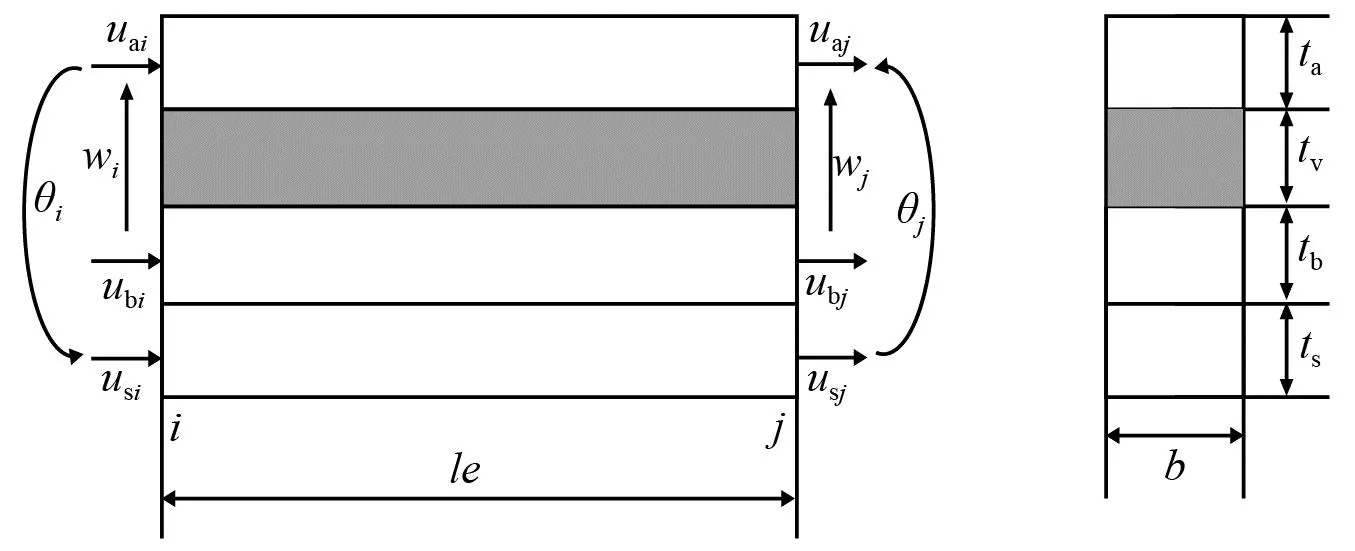
图3 ICLD梁单元

该一维两节点ICLD梁单元的长为le。每个节点有四个自由度:梁单元的横向位移、梁单元节点的转角、基梁和压电约束层的横向位移,则8自由度ICLD梁单元的位移矢量表示为

{Δe}={wi,θi,ubi,uai,wj,θj,ubj,uaj}T

(5)

单元内任意一点的位移可以由单元8自由度位移形函数通过插值唯一确定。

(6)

式中,形函数矩阵N具体由梁单元横向位移Nw、梁单元节点转角Ne、基梁Nb和压电约束层横向位移Np组成。悬臂梁单元位移分量可用形函数表示为

w=[Nw]{Δe},θ=[Nθ]{Δe}

(7)

ub=Nb{Δe},ua=Na{Δe}

(8)

于是式(2)中传感层纵向位移、黏弹性层纵向位移和剪切应变表示为

us=Ns{Δe},uv=Nv{Δe},β=Nβ{Δe}

(9)

式中,Ns,Nv,Nβ的形函数插值向量分别为

(10)

(11)

(12)

1.4 能量表达式

ICLD梁单元的能量分为动能和势能,单元各层因纵向拉伸和横向弯曲变形产生的总动能为

(13)

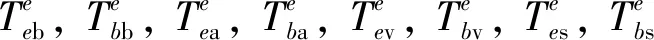
(14)

单元各层因纵向拉伸和横向弯曲变形产生的总势能为

(15)

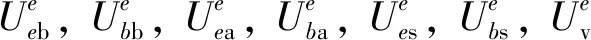
(16)

1.5 ICLD梁动力学方程

结合Hamilton变分原理推导出ICLD悬臂梁单元的动力学方程

(17)

按照常规有限元组集方法将单元质量矩阵、单元剪切刚度矩阵和单元弹性刚度矩阵组装并考虑边界约束条件得到ICLD悬臂梁结构的总动力学方程

(18)

1.6 引入GHM模型的ICLD悬臂梁动力学方程

本文采用GHM模型表征黏弹性材料的频变阻尼特性。GHM模型采用一系列微振子项的代数和来描述黏弹性材料的复剪切模量函数。微振子项通过引入耗散坐标与空间坐标耦合的方式模拟黏弹性材料应力应变行为。在拉普拉斯域中,黏弹性材料的复剪切模量函数表示为[19]

(19)

式中:G∞为正实数,表示松弛函数的稳态值;ai,ξi,ωi分别为第i阶微振子的参数,它们决定了复剪切模量函数在拉普拉斯域中形状,即能够拟合黏弹性材料复剪切模量函数曲线。

将式(18)ICLD结构动力学方程等效为一个整体单元,结合GHM模型在拉氏作用域进行拉式变换整理得到

(20)

引入耗散坐标与系统空间坐标耦合得到

(21)

结合式(20)和式(21)并对其在拉式作用域进行拉式反变换,整理得到ICLD悬臂梁结构在时域的总动力学方程

(22)

系统引入GHM模型后ICLD悬臂梁结构的总质量矩阵、阻尼矩阵、刚度矩阵、压电控制力、外部扰动力以及位移矢量分别为M,D,K,Fc,Fd,X。式中Λv,Rv分别为结构总剪切刚度矩阵正特征值组成的对角矩阵以及特征值对应的正交特征向量所组成的列向量。

2 模型降阶

本文因引入GHM模型表征黏弹性材料阻尼特性不可避免导致结构模型耦合和自由度过高,因此结构模型需要降阶处理。对于高维系统,物理空间模型降阶方法可以保留系统物理自由度,物理意义明确;状态空间模型降阶方法能够构造相应的模态空间实现非比例阻尼解耦和模态截断。因此该部分采用联合降阶法。

2.1 物理空间下自由度缩聚

本文选取的主自由度为系统的物理坐标,副自由度为系统的耗散坐标,并将式(22)中系统动力学方程改写为

(23)

本文选取的动力缩聚矩阵和迭代初值分别为

(24)

其中第i次迭代的具体值和系统动力学方程分别为

(25)

式(25)中动力学方程迭代求解出的质量矩阵、阻尼矩阵和刚度矩阵以及压电控制力矩阵具体表达为

(26)

2.2 复模态解耦与截断

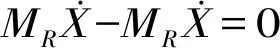
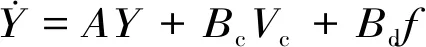
(27)

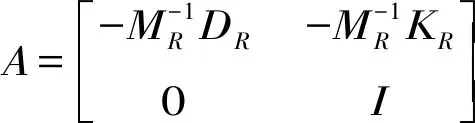
(28)

由于模态振型矩阵的振型向量之间线性无关且正交,因此式(28)中模态振型向量Y=Φξ可以作为基向量来表示物理坐标下的状态向量[20],并将式(27)改写为

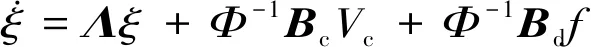
(29)

状态空间方程经模态变换后,原2n维系统动力学方程转化为n个相互独立的二维系统,实现了非比例阻尼系统解耦。由于本文主要研究ICLD悬臂梁结构的低频振动,因此只截断保留对系统特性贡献较大的低阶模态[21-22]。虽然截断后的系统维数很低,但是转换到模态空间的各矩阵都为复数,加大了控制器设计难度[23-24]。因此引入变换矩阵T将结构模型从复数空间转化到实数空间,转化后结构模型在实数空间表示为

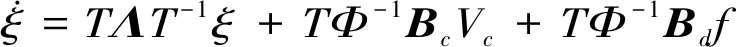
(30)

3 控制率

本部分以简化模型为对象设计了适用于线性时不变系统的最优输出反馈控制器

Vc=-GVs

(31)

式中,G为系统待确定的输出反馈增益矩阵。待确定的输出反馈增益矩阵具体由控制器的代价函数确定

(32)

式中:Q为半正定加权矩阵,表征系统的控制性能;R为正定加权矩阵,表征系统的控制成本。代价函数的目的是寻找能够有效平衡系统控制效果和控制成本的最优控制参数,即控制器的设计可以归结为寻找使代价函数最小的反馈增益矩阵G对应的加权矩阵Q和R,其中反馈增益矩阵满足Ricatti方程,系统的闭环系统方程为

(33)

4 模型验证与仿真

该部分共完成了4点工作: ①对ICLD悬臂梁结构建模并与文献[8]的结果对比,验证本文有限元建模方法的正确性; ②对结构模型进行联合降阶处理,即先在物理空间用动力缩聚方法高精度保留系统的动态特性,再在状态空间构造相应的模态空间对非比例阻尼系统进行解耦并保留系统的少数低阶模态; ③根据图1将长为0.261 6 m的悬臂梁划分为6个单元,分别在1和2单元(结构1)、3和4单元(结构2)处粘贴黏弹性材料和压电片,对比分析结构1和结构2的控制效果和控制成本; ④以结构1为研究对象,研究系统在不同激励信号下的响应以及控制效果。其中各层材料的参数如下:

基梁:总长度为0.261 6 m、宽度为0.012 7 m、厚度为0.002 286 m、弹性模量为7.1×1010Pa、密度为2 700 kg/m3。

压电层:宽度为0.012 7 m、厚度为0.000 762 m、弹性模量为7.4×1010Pa、密度为7 600 kg/m3、压电应变常数为-1.75×10-10;

首先,本文对ICLD悬臂梁结构进行有限元建模。ICLD悬臂梁结构前三阶自振频率,如表1所示。表1中:本文建模方法计算出的结构自振频率与参考文献的结果误差极小,验证了本文有限元建模方法的正确性。然后以Matlab为平台分别计算了结构1和结构2的自振频率,可以看出黏弹性层和压电层的铺设位置对悬臂梁结构自振频率有较大影响。因结构1与参考文献结构相差不大,所以结构1的自振频率与参考文献误差较小。结构2因压电片和黏弹性材料铺设位置逐渐靠近悬臂梁尖端,尖端附加质量变大导致结构的自振频率也随之变大。

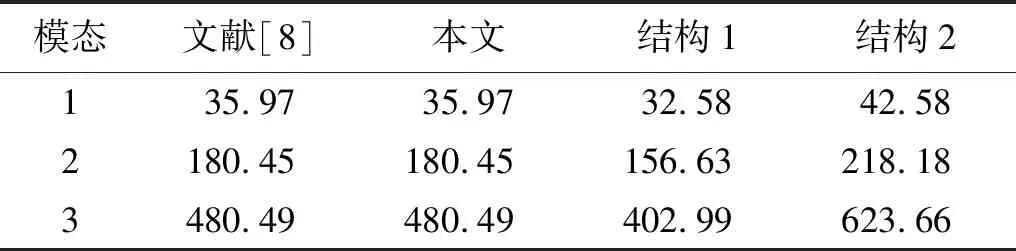
表1 ICLD悬臂梁自振频率

在本文建模方法正确的基础上,该部分以结构1为研究对象从频域角度出发验证结构模型联合降阶方法的正确性。图4为结构1模型简化前后的Bode图,横坐标以lgw为单位,纵坐标以20lg|G(jw)|为单位,代表系统状态方程的幅频特性。由图4可知,物理空间降阶法很好地保留了结构1的动态特性;模态空间截断法也较高精度地还原了结构1的低阶动态特性。结合表1的数值结果和图4的频域特性,可以验证本文ICLD悬臂梁建模方法和联合降阶方法的正确性。

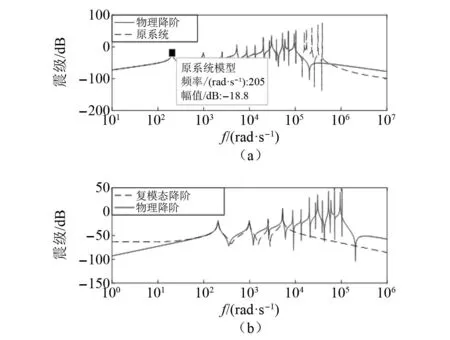
图4 结构1模型降阶

由表1可知,黏弹性层和压电层的铺设位置对结构自振频率有较大影响,因此该部分继续研究了压电片和黏弹性层的铺设位置对系统控制行为的影响。在保持控制器加权参数相同的条件下对比研究了结构1和结构2的控制行为和控制成本。

结构1和结构2在单位脉冲载荷解除后结构的响应示意图,如图5所示。

图5 结构1和结构2位移响应图

由图5可知,结构1和结构2的自由振动位移响应收敛行为和振幅没有太大的差异,但结构2的振动幅值大于结构1的振动幅值;这是由于结构1和结构2的材料参数具有一致性,并且结构2压电片和黏弹性材料的铺设位置更加接近自由端,导致结构2尖端的附加质量大,所以结构2振幅略大于结构1。在相同控制参数下,结构1和结构2响应的控制行为分别如图6和图7所示。

图6 结构1响应图

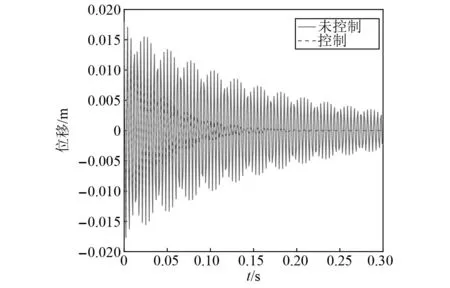
图7 结构2响应图

由图6可知,在上述控制条件下,结构1快速收敛的时间约0.15 s。

由图7可知,结构2也迅速收敛,而结构2直到0.2 s左右才收敛。另外本文还考虑了结构振动的电压控制成本,图8为结构1和结构2的控制电压对比图。

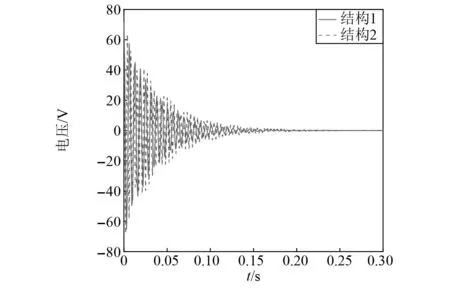
图8 结构1和结构2电压对比图

由图8可知,结构1的总控制电压小于结构2。结合图5和表1,在控制器控制参数相同的情况下,压电片层和黏弹性层的铺设位置越靠近固定端,系统控制效果越好。

除上述工作外,本文还以其他激励信号为输入再次验证简化结构模型的普遍适用性。结构1在高斯白噪声下的速度响应曲线,如图9所示。具体以结构1的第一阶模态控制高斯白噪声的振动响应,并观察控制系统的效果。由图9可知,虽然高斯白噪声属于宽频率范围激励,在随机干扰下会影响系统控制效果,但是系统响应曲线的幅度显著降低。再次验证简化结构模型的普遍适用性。

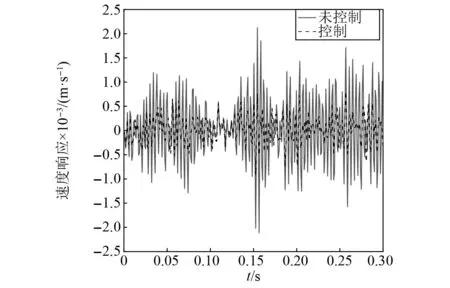
图9 高斯白噪声下系统的速度响应

5 结 论

本文主要针对ICLD悬臂梁结构的动力学建模方法、结构模型联合简化方法、压电片和黏弹性材料的位置优化以及简化模型的普遍适用性做了细致研究,得到一些有意义的结论:

(1) 在总体动力学方程的基础上引入GHM模型表征黏弹性材料的阻尼特性。不仅保证了建模方法的正确性、单元组集简单、物理意义明确并且结构模型的自由度更低。

(2) 物理空间降阶法通过构造合适的迭代矩阵,可以高精度保留原系统的低频特性,物理意义明确。状态空间降阶法,通过构造状态空间对应的模态空间实现模态解耦,独立控制截断的模态。

(3) 压电片和黏弹性材料铺设的位置对结构的振动控制效果影响较大。铺设位置越靠近自由端,悬臂梁末端附加有效质量越大,自由振动的振幅越大。在相同的控制参数下,悬臂梁末端的振动控制效果最差。相反,压电层和黏弹性层越靠近固定端,控制效果越好。

(4) 解耦后的独立模态可有效跟踪带有噪声的激励信号的响应。

本文的工作可应用于ICLD悬臂梁结构的静态特性分析、高维系统降阶以及悬臂梁结构振动主动控制。为工程上实际压电片和黏弹性层铺设位置提供了一些实际指导意义。