轴向预紧作用下的组合转子轴系模态特性研究

李维博, 王维民,2, 李 铭, 王 威, 张 帅

(1. 北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室,北京 100029;2. 北京化工大学 发动机健康监测及网格化教育部重点实验室,北京 100029;3. 北京航天动力研究所,北京 100076)

航空发动机及液体火箭发动机涡轮泵转子系统广泛采用转动部件轴向预紧装配的组合转子轴系结构[1-2]。其中转子螺纹连接以及轴向预紧力作用下各部件不同接触面间接触状态的变化是影响组合转子轴系动态特性的主要因素之一。现阶段基于有限元理论的动力学分析方法难以准确考虑螺纹连接位置以及不连续接触面之间的非线性连接参数,所以在进行组合转子轴系动力学分析时一般会忽略连接位置接触刚度和阻尼等非线性因素的影响,作为整体结构进行考虑,这不可避免地增加了理想假设下动力学简化模型的计算误差。设计阶段的计算误差需要通过制造试验件进行模态测试得到固有频率来修正初始转子动力学模型,如果制造转子后发现运行转速涉及临界转速裕度,还需要进行结构改动或面临其它昂贵的修改风险。随着我国对大推力航空发动机以及液体火箭发动机的研发,转子系统设计功率和运行转速进一步提高,准确掌握转子系统动力学特性对简化转子设计流程以及发动机整机结构优化设计技术的发展具有重要意义。基于此本文开展组合转子轴系动力学建模方法研究,以实现不同轴向预紧力作用下转子模态特性的精确计算。

组合转子轴系不连续结构包括螺纹连接以及各部件接触面连接等,其中螺纹连接结构的不确定因素主要来源于接触刚度和摩擦阻尼的非线性影响以及可能存在的螺栓松动现象[3]。典型螺栓松动的检测方法包括试验模态测试[4],冲击调制[5]以及超声检测[6]等。其中Mohamed等对不同松紧程度的螺栓试件进行模态测试表明不同张力下螺栓试件横向固有频率表现出非线性和线性特征,由此提出了一种通过横向固有频率判断螺栓紧固的方法;Milanese等[7]对螺栓松动进行研究同样表明不同连接状态下螺栓模态变化呈非线性和线性特征。

而对于转子系统中各部件接触界面连接参数对转子整体动态特性的影响,现阶段多采用等效刚度的方法将计算得到的连接参数代入动力学模型进行分析。其中常用的刚度等效方法有虚拟材料法[8]、刚度修正法[9]、零长单元以及薄层单元等。其中零长单元和薄层单元可以很好地实现接触界面法向和切向刚度阻尼特性的模拟,更加接近真实接触状态,因此得到了众多学者的青睐。零长单元通过在接触面之间施加弹簧刚度阻尼系数或改变接触系数模拟连接参数,现广泛应用于拉杆转子动特性分析中。其中饶柱石等[10]基于Hertz理论和概率统计学分析方法对粗糙平面接触刚度进行了计算,采用均布弹簧等效接触刚度建立了拉杆转子动力学模型并进行了验证;Zhang等[11]在接触面位置引入接触刚度系数,建立了拉杆转子有限元模型,通过对比不同预紧力下转子模态参数确定了接触刚度,并基于真实燃气轮机转子进行了分析验证;Gao等[12]在拉杆转子接触界面施加弹簧和铰链模拟接触界面等效抗弯刚度,并对两种接触状态下的等效刚度进行了计算。而薄层单元最早由Desai等[13]提出,起初用于表征岩石与土壤接触界面。近年来该方法在螺栓连接结构动力学建模方面得到了较多应用[14-15]。在拉杆转子建模方面,Li等[16]对不同预紧力下过盈定位配合的周向螺栓拉杆转子自由模态进行了研究分析,并根据试验结果提出了基于薄层单元进行接触界面刚度和阻尼两步优化的拉杆转子模型修正方法;缪辉等[17]采用薄层单元模拟拉杆转子复杂接触面连接参数,并运用分形模型修正方法建立了拉杆转子动力学模型。综上所述可知现阶段考虑接触界面非线性连接参数的动力学建模理论主要集中在燃气轮机拉杆转子方面,这是由于拉杆转子的整体堆叠式结构造成的,相比之下带有套筒型部件的实心转子所形成的组合转子轴系动力学特性受接触面连接参数影响较小,但该类转子往往具有超高的设计转速以及柔性转子结构,所以对其动力学特性的准确计算就显得十分重要。同时由文献[18]中对接触界面有无定位凸肩情况下接触刚度的变化研究表明组合转子轴系各部件与实心转子间接触状态的影响也不可忽略。

综上所述,本文开展轴向预紧力作用下组合转子轴系螺纹连接状态以及接触面非线性参数对转子模态特性的影响研究。首先根据组合转子轴系结构特点,将薄层单元和零长单元引入建模仿真中模拟转子各部件间接触面连接刚度和摩擦阻尼的影响。设计组合转子轴系并建立初始有限元模型,基于静态结构分析模拟非线性影响因素,采用刚度等效方法建立响应面进行薄层单元材料参数识别;然后采用GW接触模型基于轴向预紧力和各部件接触面形貌统计参数计算得到零长单元接触刚度系数,建立组合转子轴系模型进行分析。最后制造组合转子轴系试件进行模态试验验证,并对不同螺纹预紧状态以及轴向预紧力作用下的组合转子轴系模态特性进行了研究。

1 组合转子轴系结构及计算模型

1.1 组合转子轴系结构

某液体火箭发动机氢涡轮泵组合转子轴系结构示意图[19],如图1所示。该转子系统主要包括主轴、诱导轮、一级叶轮、二级叶轮、涡轮、轴承以及轴套等转动部件,各部件通过两侧压紧大螺母轴向预紧装配实现轴系整体的紧固。其中两级叶轮以及涡轮与主轴之间为中部花键传扭(粗实线)、两侧定位圆(细实线)过盈配合结构,其余轴套以及轴承等转动部件与主轴之间(虚线)均为小间隙配合结构。由图1可知组合转子轴系整体为具有多个接触界面的单主轴多部件组合结构。

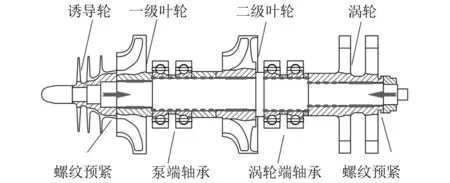
图1 某型号涡轮泵转子结构示意图

本文研究主体为轴向预紧力作用下螺纹预紧状态以及接触面连接参数对转子模态特性的影响。为确保研究主体,忽略花键配合以及过盈参数的影响,根据图1涡轮泵转子结构尺寸设计图2组合转子轴系进行研究。设计转子包括中心轴、驱动端压紧螺母、悬臂端压紧螺母、叶轮轴套、轴套1、轴套2、轴套3以及轴套4。其中中心轴中间轮盘为整体结构以考虑叶轮和涡轮过盈配合对转子的加强作用,轴承支承位置以及其它结构尺寸与涡轮泵主轴基本一致。各轴套尺寸根据涡轮泵轴套以及叶轮和涡轮轮毂等部件结构尺寸进行设计,与中心轴之间均采用小间隙定位配合,其中轴套4表示轴系支承轴承内圈。压紧螺母螺纹尺寸(M22)与涡轮泵转子一致。多个轴套套装于中心轴上通过两端压紧螺母轴向预紧实现轴系紧固。转子材料选择与涡轮泵转子一致,中心轴材料为GH4169,轴套4为45号钢,其余部件均为钛合金TC4。

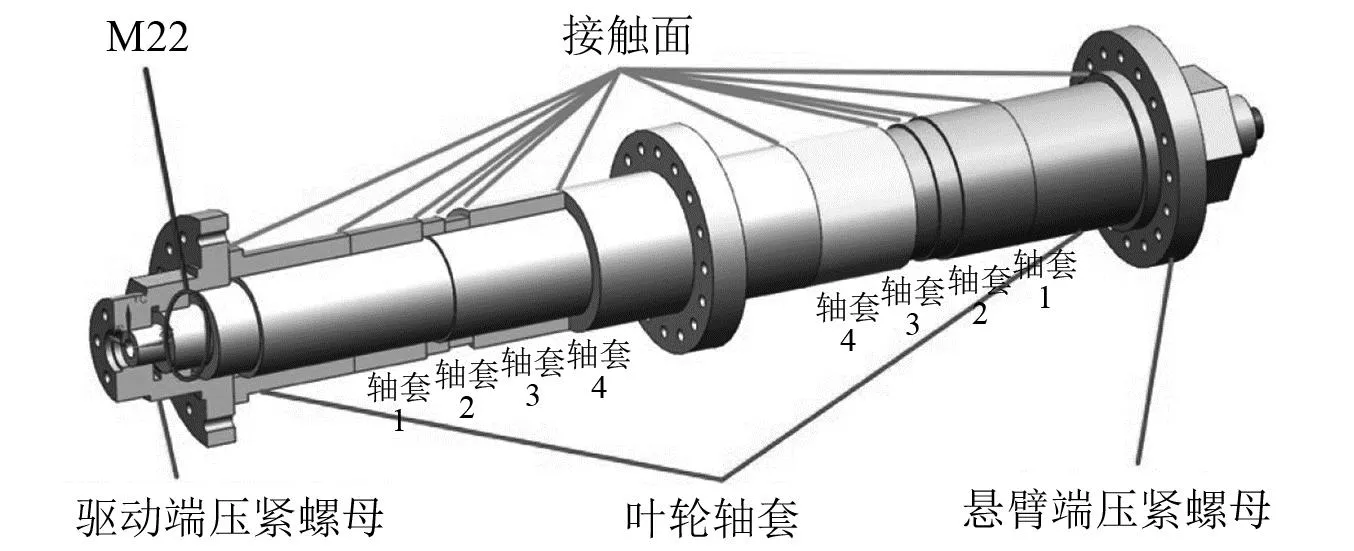
图2 组合转子轴系三维结构图

1.2 组合转子轴系有限元模型

现阶段对组合转子轴系动力学特性分析普遍采用两种建模方法:第一种是忽略转子轴套和叶轮轮毂等部件对转子整体刚度的加强作用,将各转动部件以集中质量的形式施加于转子模型进行分析,这样会降低转子的有效刚度,使得计算得到的模态频率偏小;第二种是将转子轴套和叶轮轮毂等部件与中心轴作为整体进行分析,由于忽略了接触界面对转子有效刚度的削弱作用,因此计算得到的模态频率偏大。图3所示为组合转子轴系整体结构初始有限元模型网格单元划分图,所有单元均采用8节点实体单元,网格单元总数141 232个。模型材料均选择线弹性材料,材料属性如表1所示。基于该初始有限元模型采用两种方法对组合转子轴系自由模态进行分析得到转子前两阶模态频率如表2所示,对比可知整体转子结构相对于集中质量结构前两阶模态频率仿真值误差值分别为36.8%和47.2%,差距明显,无法实现转子真实动特性的预测。

表1 组合转子轴系有限元模型材料属性

表2 两种方法下组合转子轴系前两阶自由模态频率

图3 组合转子轴系有限元模型网格划分图

为获得最大程度反映组合转子轴系真实特性的有限元模型,并得到不同轴向预紧力作用下组合转子轴系的建模方法,需要考虑转子接触面位置连接刚度和摩擦阻尼等因素的影响,对转子有限元模型进行分析和更新修正。针对组合转子轴系结构特点,区分各轴套和中心轴间接触界面以及轴向预紧力作用下压紧螺母和轴套间接触界面连接参数的影响,采用基于薄层单元和零长单元两步修正的方法进行模型优化,并通过试验进行验证。整体分析流程如图4所示。

图4 轴向预紧力作用下组合转子轴系模型优化流程图

2 模型优化理论

2.1 薄层单元基本理论

薄层单元仿真法即为在组合结构接触面之间定义虚拟材料层来模拟接触面之间力学特征的方法,为使用宏观结构表征微观接触行为,虚拟材料层采用厚度很小的薄层单元。组合转子轴系各轴套与中心轴之间始终保持接触,接触界面刚度和摩擦阻尼等产生的作用力可表现为薄层单元上切向和法向的载荷,通过在接触表面引入线性本构关系的薄层单元可将接触面的复杂接触关系进行线性等效。

结构上薄层单元厚度远小于其长度和宽度,假设总体坐标系内薄层单元尺寸为l1×l2×t,由虚位移原理得到虚功方程

δW=∭V{σ}T{δε}dV=δ{u}TK{u}

(1)

式中:V为薄层单元体积;σ为单元应力;ε为单元应变; {u}为单元节点位移;K为薄层单元刚度矩阵。则刚度矩阵K可表示为

(2)

式中:B为变换矩阵;D为材料本构矩阵;通过等参变换将薄层单元坐标系由总体坐标系转换为局部坐标系进行表示,此时单元刚度矩阵K表示为

(3)

式中:ξ、η、ζ为局部坐标系符号;J为单元雅可比矩阵,表示总体坐标与局部坐标间的偏微分关系,数值积分求解简化为

(4)

将式(4)代入式(3),采用高斯积分公式进行计算[20]可得到薄层单元刚度矩阵K表达式为

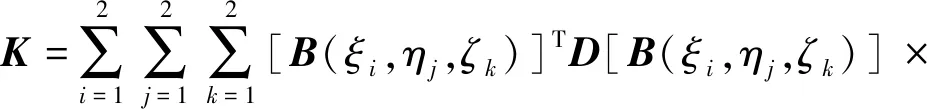
(5)

式中,wξ,i、wη,j、wζ,k为高斯积分权函数。

在有限元计算中,采用各向同性材料模拟薄层单元,其本构方程可表达为

(6)

式中:λ为拉梅常数;G为材料剪切模量。

(7)

(8)

式中:E为材料弹性模量;μ为泊松比。

对于薄层单元,其厚度远小于其他两个方向的特征尺寸。由文献[13]可知,当材料泊松比为0时,薄层单元的法向刚度和切向刚度将会解耦,此时可忽略薄层单元两个特征尺寸方向的内应变分量(εx、εy、γxy)。假设连接界面法向和切向接触性能相互独立,且两切向接触性能相同,则薄层单元材料本构方程表达为

(9)

由式(7)和式(9)可知各向同性材料中仅有两个可变参数:材料弹性模量E和材料剪切模量G。这两个参数共同决定接触界面连接参数。

根据薄层单元假设理论,需要确定合理的单元厚度,厚度过大会使得材料本构矩阵D出现耦合项,产生各个方向的耦合刚度,无法准确模拟接触面力学特征,厚度接近0会使雅可比矩阵J趋于0,使得求逆困难,无法求解变换矩阵B。对于材料为线性本构关系的薄层单元,其厚度可采用单元网格尺寸比例系数ρ进行选择,比例系数ρ表达为

(10)

研究表明薄层单元尺寸比例系数在10～100内具有较好的效果,本文通过控制组合转子轴系径向接触面薄层单元网格划分尺寸将单元尺寸比例系数控制在该范围内。

2.2 接触刚度理论

实际中零部件的表面并不是理想的光滑平面,而是具有一定的表面误差,包括形位误差、波纹度以及粗糙度。组合转子轴系零部件为精加工结构,表面误差主要为粗糙度,各轴套接触面可看作光滑平面上分布有一系列微凸体的粗糙表面。轴向预紧力作用下各轴套间的接触过程实际为两粗糙表面微凸体相互挤压发生形变的过程。

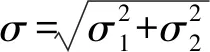
(11)

式中:r1和r2分别为两粗糙表面微凸体平均曲率半径;E1和E2、μ1和μ2分别为两粗糙表面弹性模量和泊松比。

取粗糙表面微凸体高度分布均值线作为基准线,光滑刚性表面到基准线距离为d,粗糙表面微凸体顶点到基准线距离为z。粗糙表面微凸体概率密度函数为φ(z)。假设名义接触面积A0(宏观接触表面)中有N个微凸体顶点,则在光滑刚性表面位置接触的微凸体顶点数为

(12)

由Hertz接触理论可知每个微凸体接触面积为a=πr(z-d),则实际接触面积A和法向总载荷W为

(13)

(14)

将上式中变量d和z通过h=d/σ和s=z/σ进行标准化为

A=πNrσF1(h)

(15)

(16)

其中,

(17)

设n=N/A0为单位名义接触面积上的微凸体数,由于接触发生在名义接触面积A0内,由式(16)可得单位名义接触面积压力p为

(18)

由式(18)可知,在两接触表面特征参数一定时,单位接触面积压力p与两接触表面标准化距离h呈非线性函数关系,当h在某一特定值附近做小幅度变动时,两者可近似表现为通过某一刚度系数进行表征的线性函数关系,在有限元分析当中该刚度值可采用法向接触刚度系数来表示。对式(18)两端取接触面距离d的微分,可得

dp=-2Enr1/2σ1/2F1/2(h)d(d)

(19)

由式(19)可知单位名义接触面积法向接触刚度系数k可表示为

k=2Enr1/2σ1/2F1/2(h)

(20)

基于以上理论可求得轴向预紧作用下组合转子轴系压紧螺母和各轴套间的接触刚度。

3 组合转子轴系模型建立

3.1 基于静态结构分析的薄层单元参数识别

在组合转子轴系动力学分析中,材料弹性模量和剪切模量会对转子模态刚度产生影响,密度会对转子模态质量产生影响。由于模态分析无法定义非线性因素,且组合转子轴系各轴套和中心轴之间的接触状态难以准确估计,因此采用静态结构分析方法表征接触界面非线性影响,将薄层单元弹性模量作为设计优化变量,通过提取初始组合转子轴系有限元模型两侧悬臂端弯曲刚度,对薄层单元材料参数进行识别,实现组合转子轴系等效模化。

采用多步准静态分析对初始组合转子轴系有限元模型进行分析。将转子轴向各轴套接触位置节点直接融合看作整体结构。由于转子径向各轴套与中心轴之间为小间隙配合,存在微动摩擦现象,根据转子0.8～1.6的加工粗糙度并考虑装配磨损,各轴套与中心轴之间接触状态采用有摩擦接触,摩擦因数设置为0.15。转子中间轮盘位置施加固定约束。在两侧压紧螺母径向施加500 N集中载荷,提取转子两侧悬臂端弯曲刚度。图5所示为集中载荷作用下初始组合转子轴系有限元模型形变云图。由图5可知组合转子轴系两侧悬臂端等效弯曲刚度约为2.16×107N/m。

图5 集中载荷下初始组合转子轴系模型形变云图

在组合转子轴系各轴套与中心轴接触面位置建立薄层单元。根据组合转子轴系结构特点,叶轮轴套和轴套1与中心轴对应接触位置薄层厚度选择0.5 mm,轴套2、轴套3和轴套4与中心轴对应接触位置薄层厚度选择0.25 mm。为保证有限元计算的准确性,除薄层单元以外的模型网格划分尺寸与初始组合转子轴系有限元模型一致,网格尺寸控制在1.5 mm左右,薄层单元厚度方向分别设置为五层网格和三层网格,此时叶轮轴套和轴套1与中心轴之间薄层单元厚度0.1 mm,单元尺寸比例系数为15;轴套2、轴套3和轴套4与中心轴之间薄层单元厚度0.083 mm,单元尺寸比例系数为18,满足薄层单元理论要求。包含薄层单元的组合转子轴系有限元模型如图6所示,网格单元总数为179 008个,所有接触均为绑定接触。

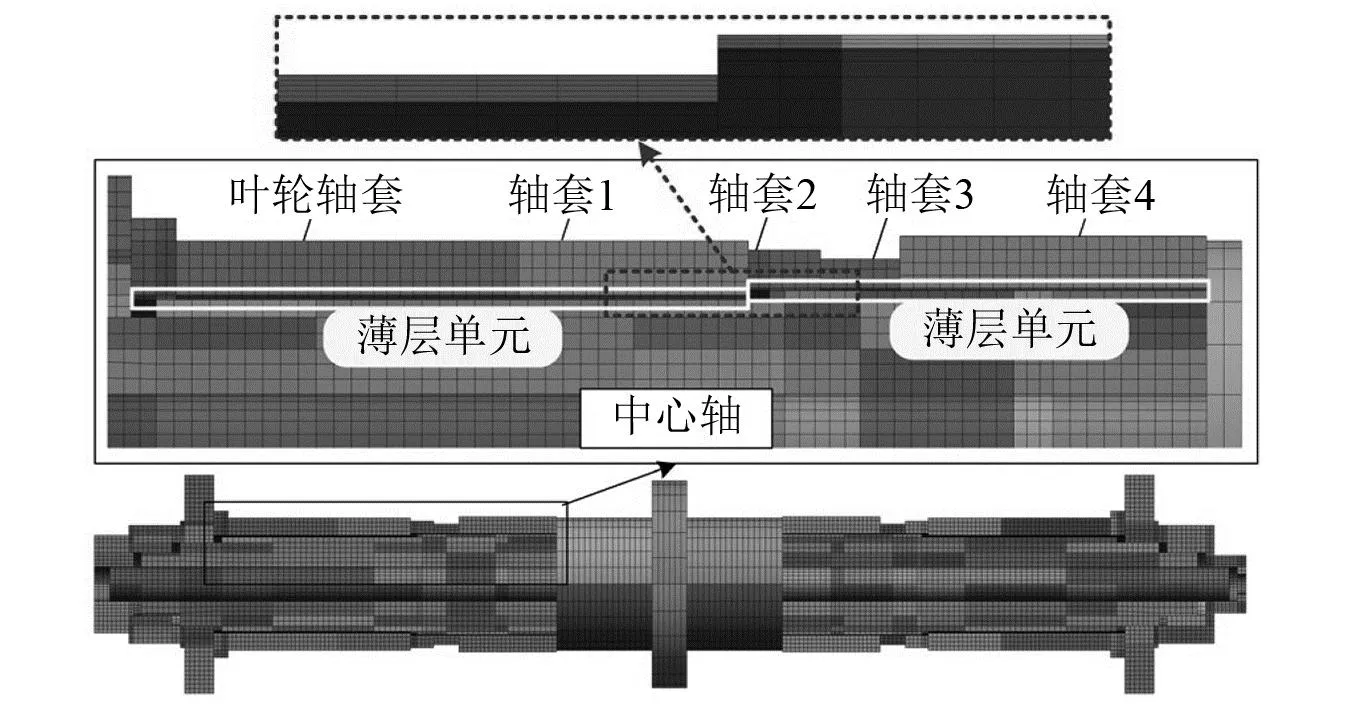
图6 采用薄层单元的组合转子轴系模型

薄层单元材料采用线弹性材料,初始材料参数与各轴套材料一致。根据静态结构分析结果基于响应面优化方法对薄层单元材料参数进行识别,识别得到叶轮轴套、轴套1、轴套2和轴套3位置所对应薄层单元等效弹性模量为28.73 MPa,轴套4位置所对应薄层单元材料等效弹性模量为1.63 MPa。由所得薄层单元材料参数建立组合转子轴系有限元模型,根据不同轴向预紧力作用下组合转子轴系各轴套接触状态的变化,考虑两种极限状态进行模态计算,低轴向预紧力作用下各轴套接触面可看作不连续状态,高轴向预紧力作用下各轴套可看作整体结构。对两极限状态下的薄层单元组合转子轴系有限元模型自由模态进行分析得到前两阶固有频率如表3所示。对比可知两种状态下转子模态特性差异明显,说明转子轴向各部件接触面连接参数对转子模态特性具有很大影响。

表3 不同工况薄层单元组合转子轴系仿真与试验结果

3.2 部件轴向接触面刚度参数

根据接触刚度理论,为得到轴向预紧力作用下组合转子轴系轴向各部件接触刚度系数,需要得到不同拧紧力矩下压紧螺母产生的轴向预紧力以及各部件接触面的表面形貌统计参数。

本文采用扭矩法进行压紧螺母轴向预紧力测试,工程上螺栓拧紧力矩和轴向预紧力之间的关系可近似采用“扭矩系数”来表示,两者关系可近似表达为

Tin=KbDFp

(21)

式中:Tin为螺栓拧紧力矩;Fp为轴向预紧力;D为螺栓名义直径;Kb为扭矩系数,该系数与螺纹尺寸、形状以及摩擦因数等因素有关。

为验证式(21)的合理性并得到准确的扭矩系数,设计如图7(a)所示的组合转子轴系轴向预紧力测试装置,采用数显力矩扳手(17～340 N/m,精度2%)和环形测力传感器(0～10 t,精度0.05%)对不同拧紧力矩下压紧螺母所产生的轴向预紧力进行测试。得到不同拧紧力矩(20～200 N/m)下压紧螺母产生的轴向预紧力大小如表4所示。对数据进行拟合可知组合转子轴系M22压紧螺母拧紧力矩和轴向预紧力之间的关系可采用扭矩系数法进行表示,扭矩系数Kb近似等于0.35。

表4 压紧螺母不同拧紧力矩下的轴向预紧力大小

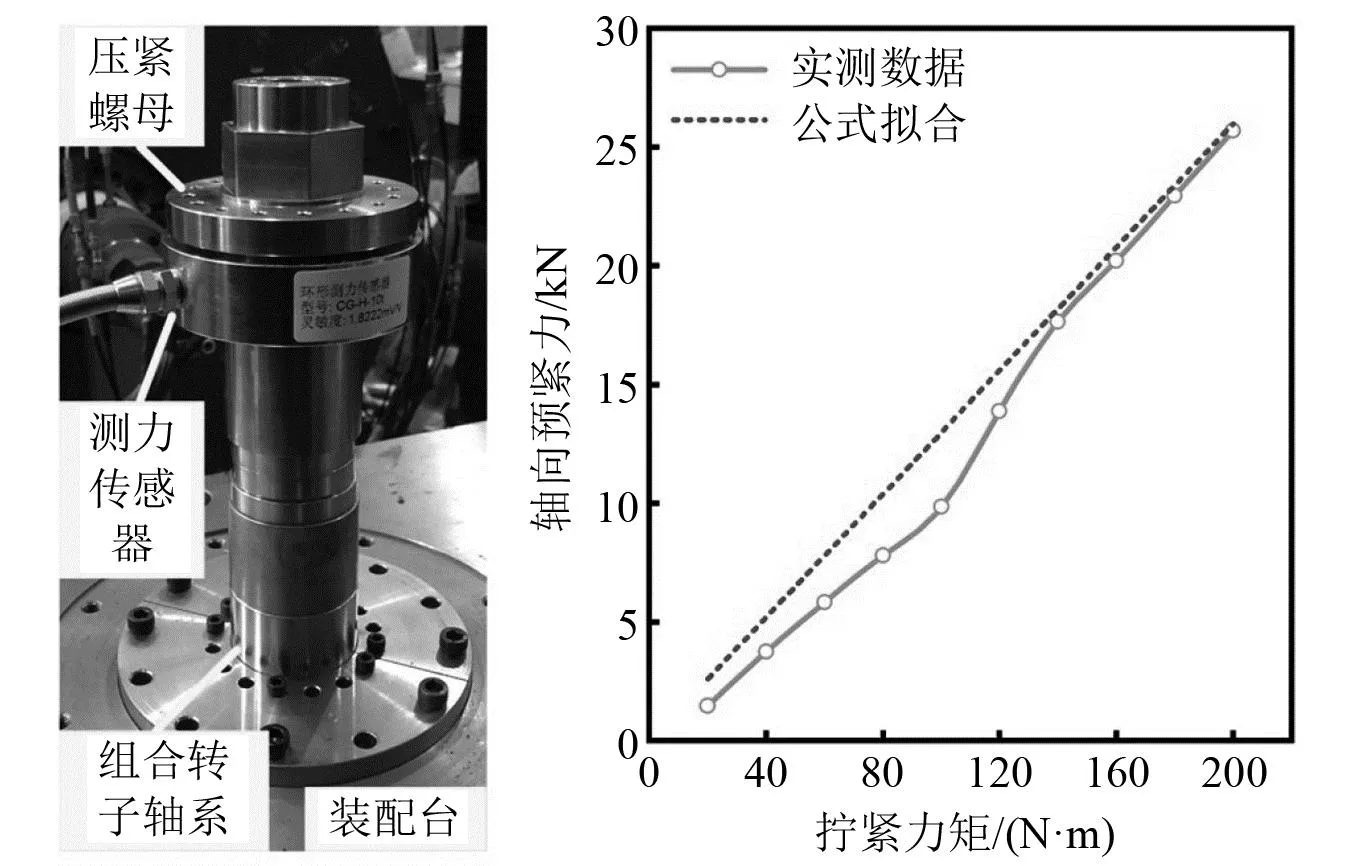
图7 轴向预紧力测试装置及测试数据

根据组合转子轴系实际结构特点,转子各部件轴向接触面设计粗糙度Ra为0.8 μm,试件加工过程严格按照设计要求进行加工。文献[23]中对不同机加工方式下所得标准样块的表面轮廓数据进行了测量,得到了不同粗糙度下的金属表面形貌统计参数,由于本文转子试件加工结构较为简单,相同机加工方式下可认为试件轴向接触表面形貌统计参数与标准样块一致,因此可得到转子各部件轴向接触表面形貌统计参数如表5所示。基于接触刚度理论,根据表4和表5数据计算得到不同拧紧力矩下组合转子轴系各接触面接触刚度如图8所示。

表5 各轴套接触面表面形貌统计参数

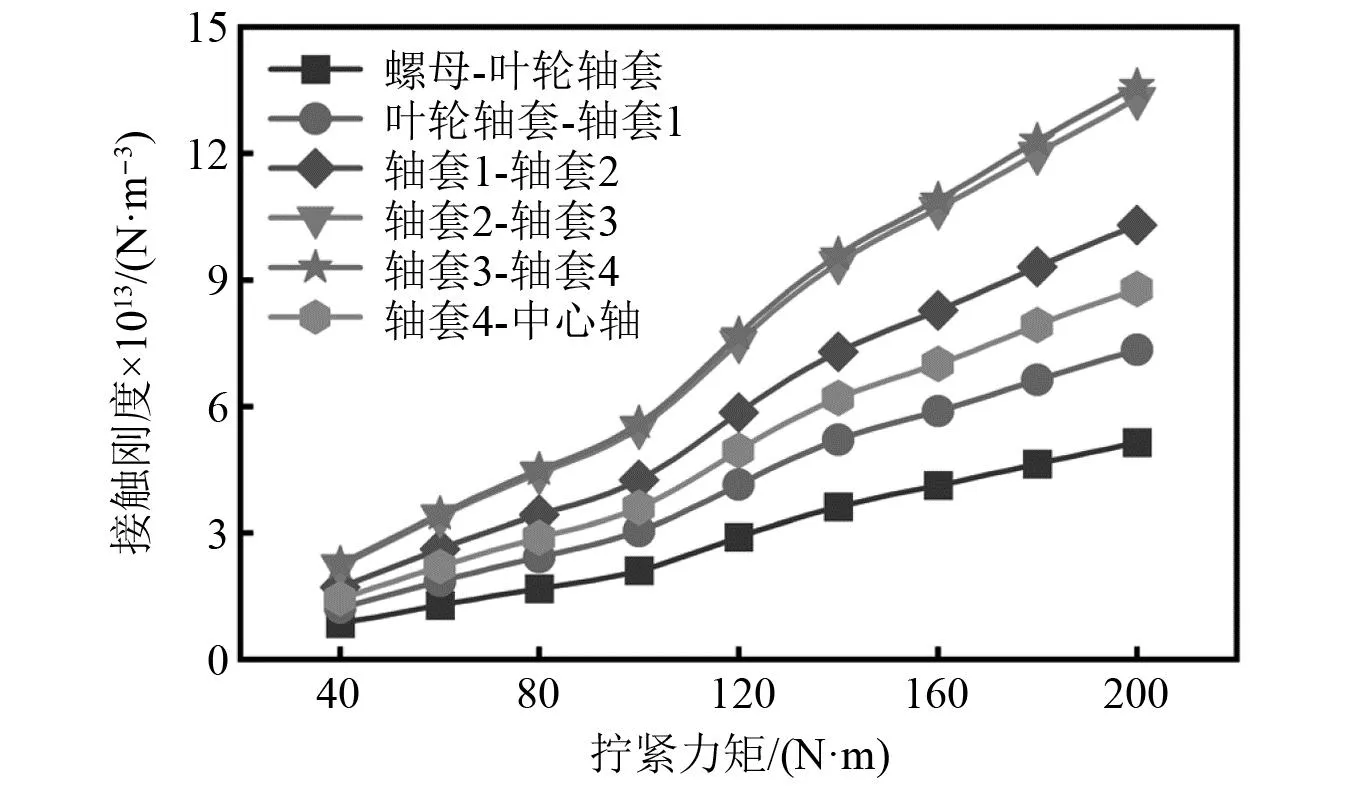
图8 不同拧紧力矩下组合转子轴系各接触面接触刚度

3.3 组合转子轴系优化模型

将计算所得不同拧紧力矩下组合转子轴系轴向各接触刚度通过法向接触刚度系数的形式施加于采用薄层单元优化的组合转子轴系有限元模型各部件轴向接触界面,不同接触界面刚度系数施加位置如图9所示。

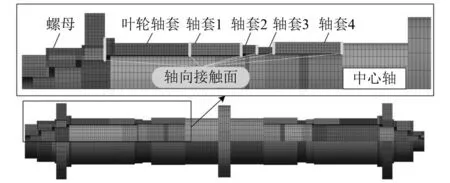
图9 组合转子轴系轴向接触刚度施加位置

对不同拧紧力矩下组合转子轴系自由模态进行计算得到前两阶固有频率如图10所示。由图可知组合转子轴系前两阶固有频率随拧紧力矩的增加而非线性地增大,整体分别增大5.92%和7.58%,说明轴向预紧作用下组合转子轴系各部件接触面连接状态对转子二阶固有频率影响较大。此外,由于模态分析中假设的阻尼模型很难反应真实的阻尼情况,因此采用试验测试方式来研究轴向预紧作用对组合转子轴系阻尼的影响情况。

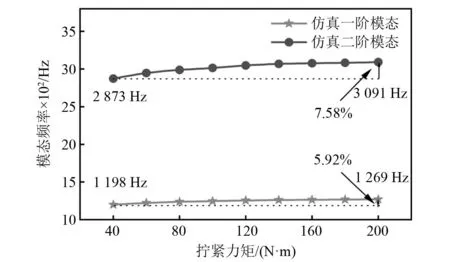
图10 不同拧紧力矩下组合转子轴系优化模型前两阶模态频率

4 试验模态研究

4.1 试验装置

为验证上述模型优化理论的正确性,进行轴向预紧力作用下的组合转子轴系自由模态试验研究。考虑到实际边界条件以及转子试件材质不均等带来的不确定因素以及螺纹连接结构产生的非线性影响因素。采用中心轴试件、螺纹连接转子试件以及组合转子轴系试件三种情况分别进行模态测试,不同转子试件结构如图11所示。

图11 三种情况转子试件结构图

试验过程中测试转子采用弹性绳悬挂以模拟自由边界条件,悬挂位置为组合转子轴系实际支承位置(轴套4相应位置)。利用LMS数据采集设备采用单点激振,多点拾取的方式进行测试,频率范围选择0～4 096 Hz,分辨率0.5 Hz。为避免传感器附加质量对模态参数的影响,并充分反映测试转子模态信息,选用3个加速度传感器,根据转子结构特点轴向选取15个敲击点,加速度传感器安装位置尽可能避开转子节点位置。试验测试装置以及测试转子测点分布位置如图12所示。三种情况下对转子试件每个敲击点均进行五次敲击,得到激振力作用下各响应点的频响函数(frequency response function, FRF),通过分析得到测试转子固有频率、模态阻尼比和振型。

图12 试验转子自由模态测试图

4.2 中心轴试件模态试验

中心轴作为组合转子轴系主体部分,不含非线性影响因素,对其自由模态进行测试分析得到激振力作用下各响应点的FRF和函数曲线如图13所示。FRF和函数能合理识别测试范围内转子各阶模态,响应峰值采用db形式可使得各阶模态特征更加明显。由结果可知0～4 096 Hz范围内FRF和函数曲线具有两个关于共振峰基本对称的明显峰值,说明FRF和函数具有很好的线性特征。两峰值对应的横向振型为弯曲振型,说明该带宽范围内中心轴试件具有两阶弯曲模态,无刚性振型。其中一阶模态频率为1 358 Hz,阻尼比0.13%。二阶模态频率为3 034 Hz,阻尼比0.56%。基于初始组合转子轴系有限元模型对中心轴进行分析得到其前两阶固有频率如表6所示,对比试验数据可知,中心轴转子前两阶固有频率相比试验值误差分别为1.25%和0.03%,误差很小,表明了材料属性以及有限元模型的合理性。

表6 中心轴转子前两阶自由模态试验与仿真结果

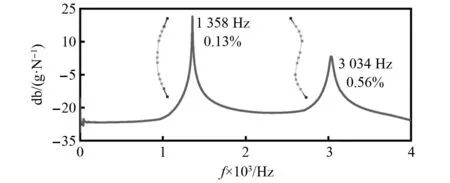
图13 自由边界条件下中心轴试件FRF和函数曲线

4.3 螺纹连接转子试件模态试验

组合转子轴系采用压紧螺母轴向预紧的方式实现整体结构的紧固,其中螺纹连接位置由于内外螺纹相对转动磨损以及接触面塑性变形、表面嵌入和蠕变等不确定因素产生的接触区域刚度和阻尼的非线性变化会对转子模态特性产生一定影响。为剔除螺纹预紧状态对组合转子轴系自由模态的影响,将两侧压紧螺母安装于中心轴作为螺纹连接转子试件,对两侧压紧螺母分别施加40～200 N/m(间隔40 N/m)拧紧力矩后进行模态测试,得到自由边界条件下不同拧紧力矩作用的转子试件前两阶模态特性。图14示出了拧紧力矩分别为40 N/m、120 N/m和200 N/m下的螺纹连接转子试件模态频响函数。由图14可知,拧紧力矩为40 N/m时转子试件FRF和函数两共振峰右侧会出现较明显侧峰,随着拧紧力矩的上升,侧峰逐渐减小,当拧紧力矩为200 N/m时侧峰基本消失,两峰值关于共振峰基本对称,说明频响函数共振峰的不对称性为螺纹松连接状态下的非线性影响所导致的,且螺纹紧连接状态会很大程度上降低该非线性对转子试件模态特性的影响,使得螺纹连接转子趋近于动力学连续转子。

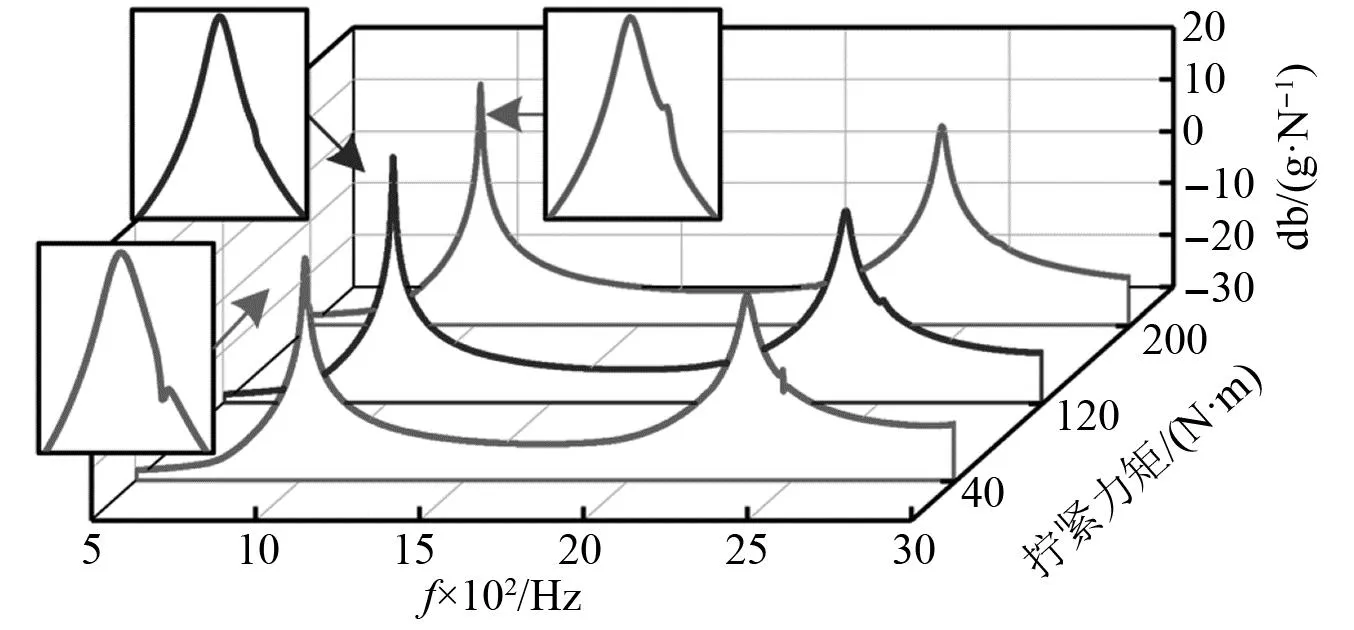
图14 不同拧紧力矩下螺纹连接转子试件FRF和函数曲线

图15和图16分别反映了拧紧力矩为40～200 N/m范围内螺纹连接转子试件前两阶固有频率和模态阻尼比的变化情况。由图15可知,自由边界条件下随着拧紧力矩的增大,转子试件一阶固有频率基本不发生变化,二阶固有频率有2.7%的小幅度上升。且当拧紧力矩大于80 N/m时转子试件一阶固有频率稳定在1 020 Hz,此时一阶模态共振峰基本对称;当拧紧力矩大于160 N/m时转子试件二阶固有频率趋于稳定,二阶模态共振峰基本对称。说明螺纹连接状态变化引起的非线性因素对转子试件二阶固有频率影响较为明显,当拧紧力矩大于160 N/m时,螺纹连接结构产生的非线性影响可基本忽略。此外,由图16可知,转子试件前两阶模态阻尼比相较固有频率对拧紧力矩表现出更为敏感的特性,随着拧紧力矩的增大而减小,但变化趋势与固有频率一致,一阶阻尼比在拧紧力矩80 N/m后趋于稳定,二阶阻尼比在拧紧力矩160 N/m后趋于稳定,这证实了模态测试结果的可靠性。同时模态阻尼比的降低是由于螺纹连接表面由微滑移状态过渡为黏滞状态使得转子试件内部摩擦阻尼降低而引起的。

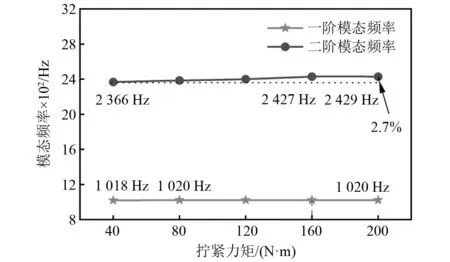
图15 不同拧紧力矩下螺纹连接转子试件前两阶模态频率

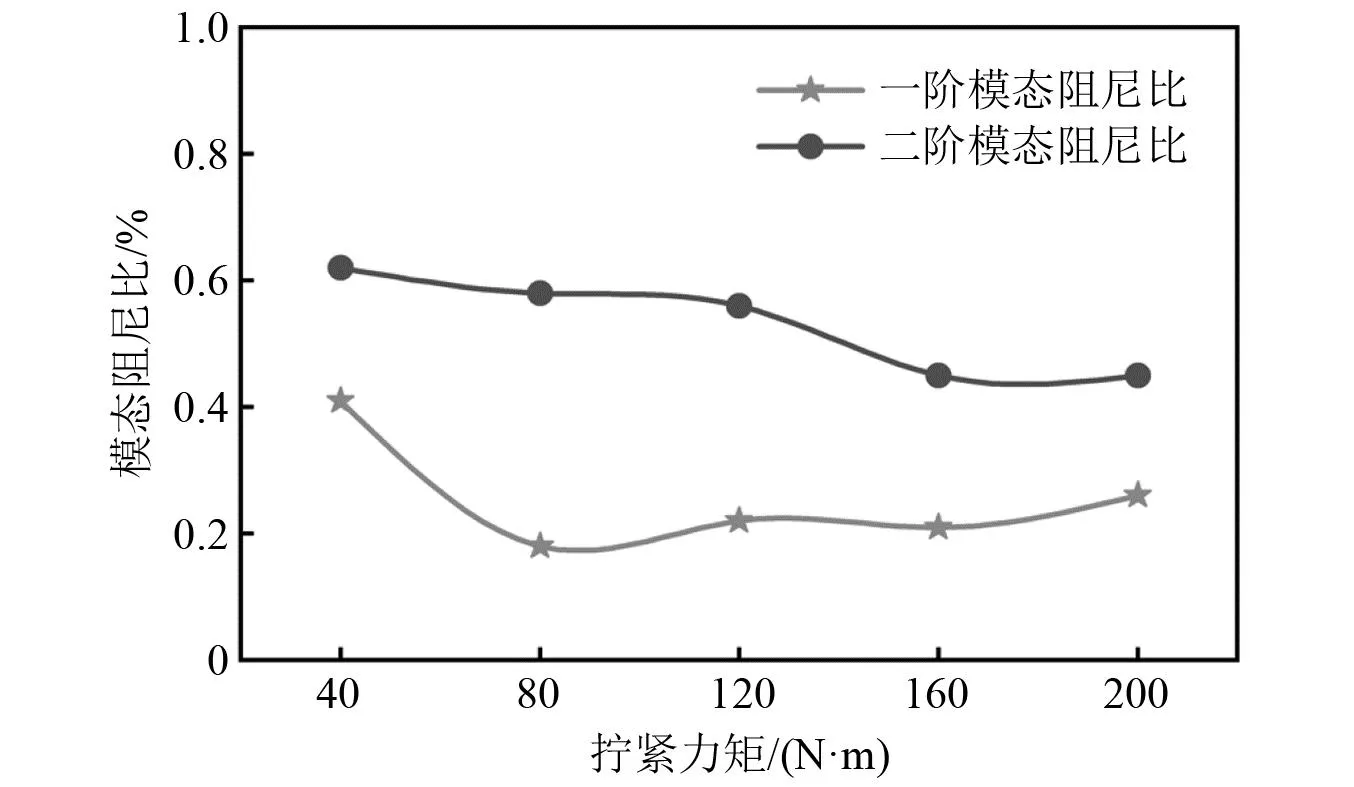
图16 不同拧紧力矩下螺纹连接转子试件前两阶模态阻尼比

基于初始组合转子轴系有限元模型采用动力学整体结构对螺纹连接转子进行分析得到其前两阶固有频率如表7所示,相应模态振型如图17所示。选择拧紧力矩为200 N/m时的螺纹连接转子试件前两阶模态参数进行对比,可知固有频率仿真值与试验值误差为0.29%和1.28%,模态振型基本一致,误差很小,说明该组合转子轴系螺纹连接结构对转子整体刚度削弱作用较小。同时由模态试验可知该组合转子结构中螺纹连接状态对转子模态特性影响较小,因此在组合转子轴系建模时可忽略螺纹连接结构的影响,作为整体结构进行分析。

表7 螺纹连接转子前两阶自由模态试验与仿真结果

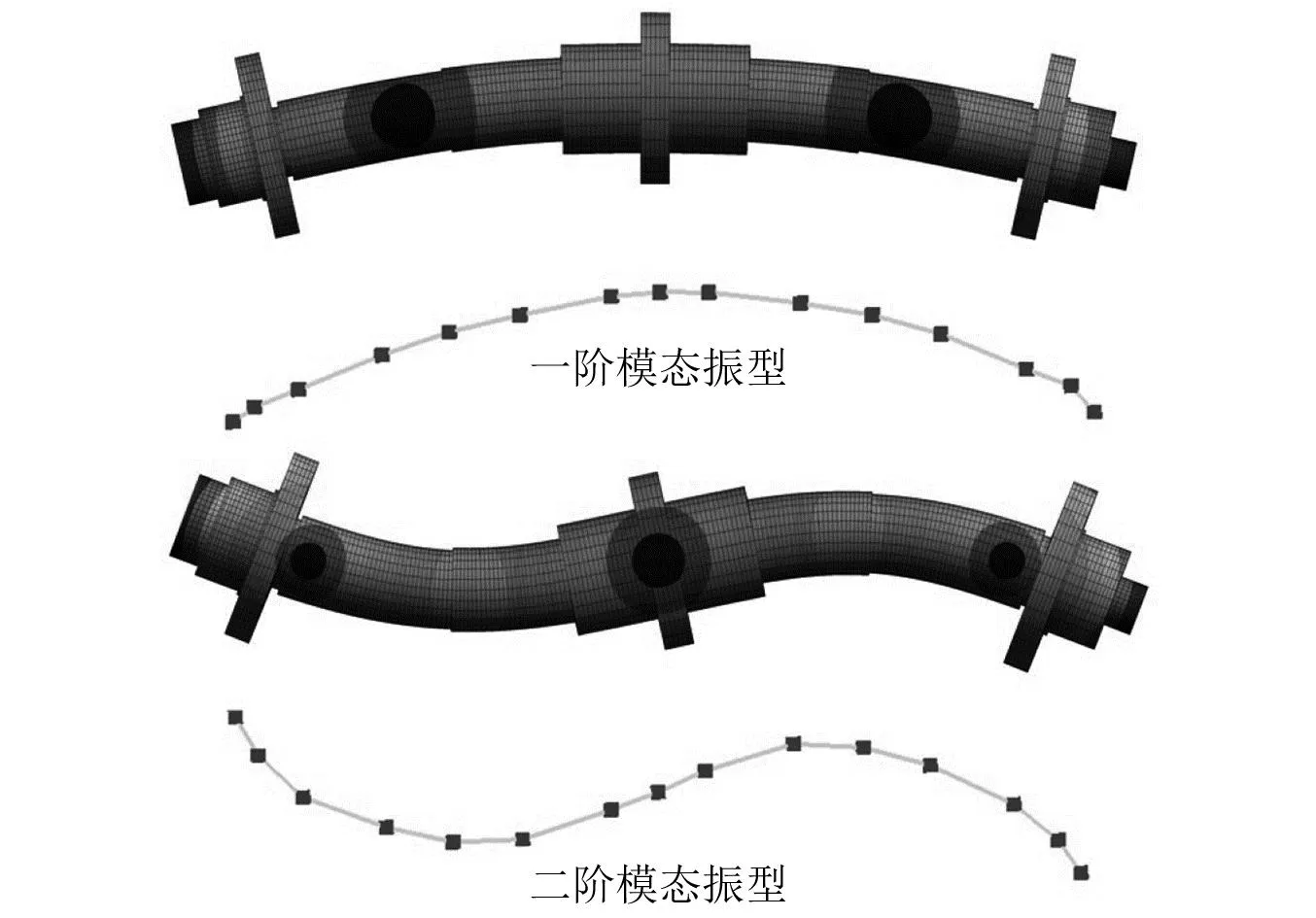
图17 大拧紧力矩下螺纹连接转子前两阶模态振型仿真结果及试验结果

4.4 组合转子轴系模态试验

对组合转子轴系试件两侧压紧螺母分别施加40～200 N/m(间隔20 N/m)拧紧力矩,测试自由边界条件下组合转子轴系试件前两阶模态特性。图18所示为拧紧力矩分别为40 N/m、120 N/m和200 N/m下的组合转子轴系试件模态频响函数。由图18可知,拧紧力矩为40 N/m时转子试件FRF和函数一阶模态共振峰右侧出现较明显侧峰,二阶模态共振峰右侧出现轻微侧峰;拧紧力矩为120 N/m和200 N/m时两峰值关于共振峰具有较好对称性。对比图14螺纹连接转子试件频响函数曲线可知螺纹连接非线性对组合转子轴系试件模态特性影响较小,只有在松螺纹连接状态下频响函数曲线才会表现出一定的非线性影响特征。说明轴向预紧作用下的组合转子轴系试件模态特性受部件接触面连接参数影响较大,而螺纹连接状态的影响可忽略。

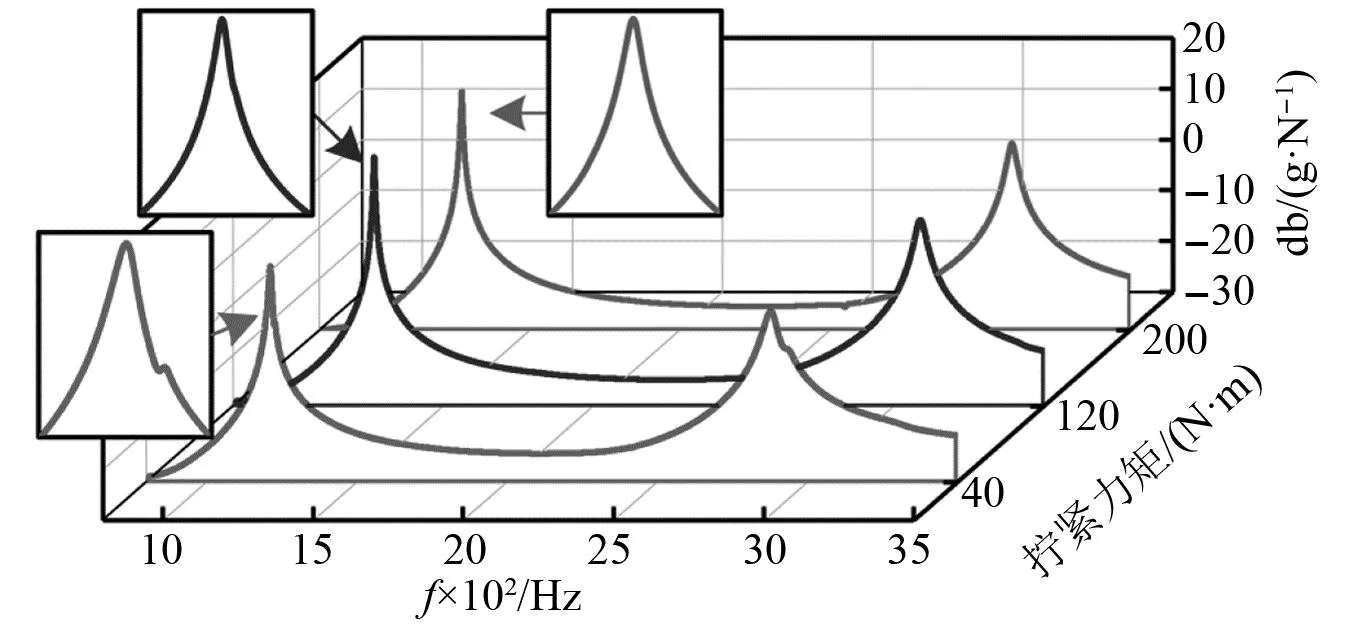
图18 不同拧紧力矩下组合转子轴系试件FRF和函数曲线

图19和图20分别为拧紧力矩40～200 N/m组合转子轴系试件前两阶固有频率和模态阻尼比的变化情况。由图19可知,自由边界条件下转子试件前两阶固有频率随拧紧力矩的增加而非线性地增大,整体分别增大5.19%和8.03%。通过变化规律可近似分为三个线性变化阶段:拧紧力矩40～80 N/m两阶固有频率较快增大;80～160 N/m增大较慢;高于160 N/m后基本稳定不变。同时部件接触面连接状态对转子试件二阶固有频率影响较大。当拧紧力矩大于160 N/m时,接触面连接参数产生的非线性影响可基本忽略。此外,由图20可知组合转子轴系试件前两阶模态阻尼比随着拧紧力矩的增大而减小,同样在160 N/m后趋于稳定。其中二阶模态阻尼比对拧紧力矩变化较为敏感,这是由于低拧紧力矩下激起的二阶弯曲振型使得转子各部件轴向接触面间相互摩擦使得阻尼增大而产生的,随着拧紧力矩增大摩擦状态过渡为黏滞状态,阻尼减小。

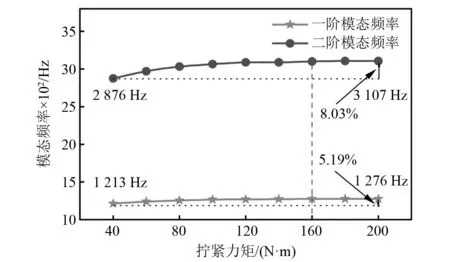
图19 不同拧紧力矩下组合转子轴系试件前两阶模态频率

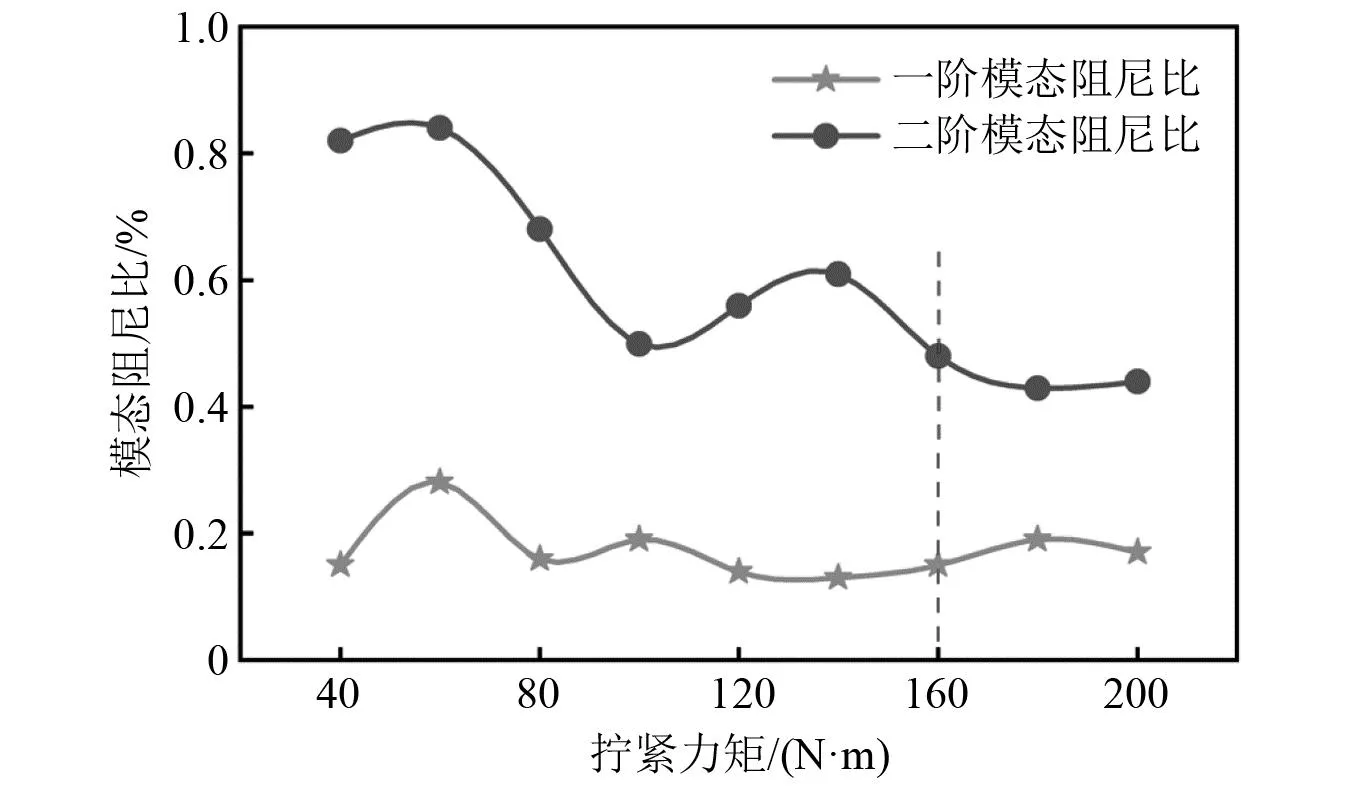
图20 不同拧紧力矩下组合转子轴系试件前两阶模态阻尼比

表8为不同拧紧力矩下组合转子轴系前两阶自由模态固有频率试验值以及本文优化模型分析所得到的仿真值,图21为拧紧力矩200 N/m时组合转子轴系前两阶模态振型仿真及试验结果对比图,对比可知该方法可以很好地反映出不同轴向预紧力作用下组合转子轴系模态参数。图22为固有频率仿真结果相比试验结果的误差值,可知不同拧紧力矩下仿真结果误差均在2%以内,并且在组合转子轴系拧紧力矩高于160 N/m的模态参数线性变化范围内仿真结果误差在1%以内,具有较高的精确性,表明了该建模方法的正确性和有效性。

表8 不同拧紧力矩组合转子轴系前两阶自由模态试验与仿真结果

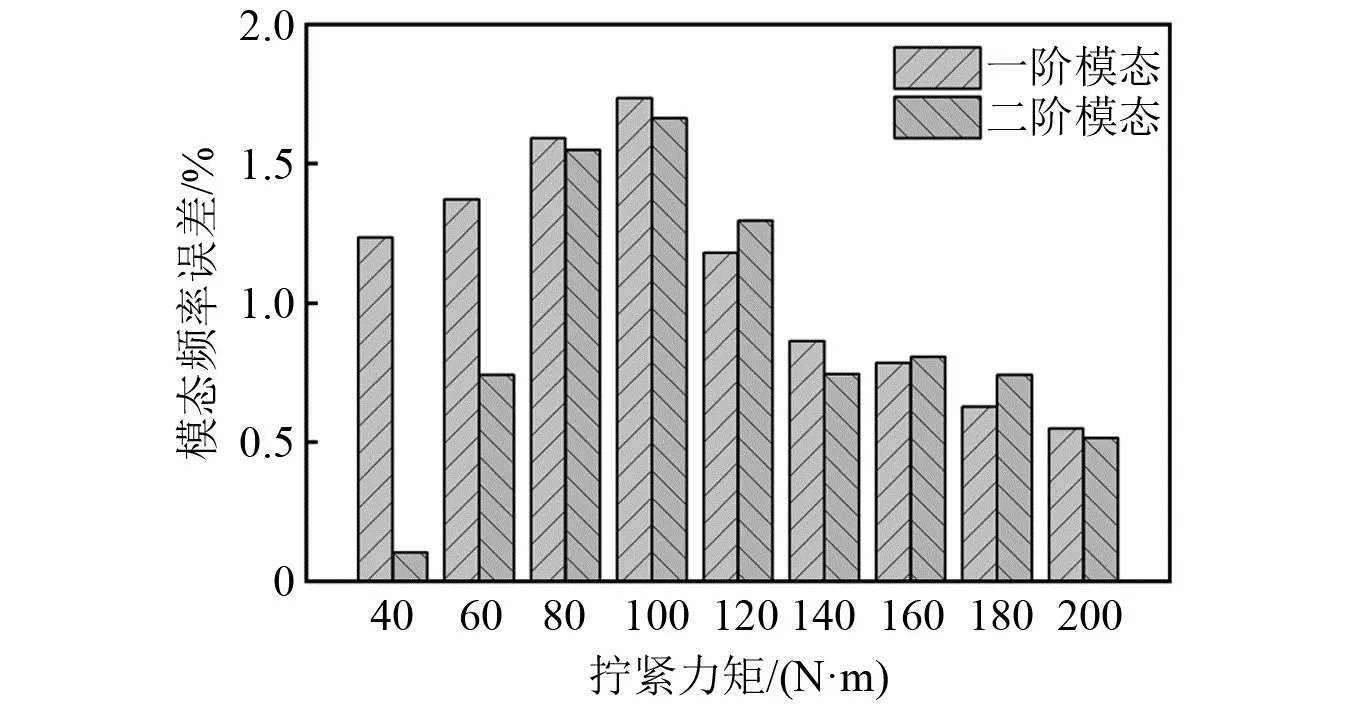
图22 不同拧紧力矩下组合转子轴系模型前两阶模态频率仿真值误差

5 结 论

本文进行轴向预紧力作用下的组合转子轴系螺纹连接状态以及接触面非线性参数对转子模态特性的影响研究,得到以下结论:

(1) 建立了基于薄层单元和零长单元两步修正的组合转子轴系动力学建模方法,仿真结果表明该方法可很好地反映出不同轴向预紧力作用下组合转子轴系模态参数变化趋势,对比试验结果可知不同拧紧力矩下仿真结果误差均在2%以内,在拧紧力矩高于160 N/m的模态参数线性变化范围内仿真结果误差小于1%。

(2) 所研究组合转子轴系螺纹连接结构对转子整体模态特性影响较小,随着螺纹紧固二阶模态频率有小幅度增加,模态阻尼比较为敏感,整体呈下降趋势。同时螺纹松连接状态会引入非线性影响因素,使得转子频响函数共振峰出现不对称性。

(3) 组合转子轴系模态特性受各部件接触面连接参数影响较大,螺纹连接影响可忽略。转子前两阶模态频率随着轴向预紧力的增加而非线性地增大,模态阻尼比呈下降趋势,其中二阶模态较为敏感。

(4) 组合转子轴系压紧螺母装配拧紧力矩需大于160 N/m,使得转子模态特性趋于稳定。