双体小行星系统平衡态与稳定性研究
杜燕茹,李翔宇,韩宏伟,乔 栋
(1.北京理工大学宇航学院,北京 100081;2.深空自主导航与控制工信部重点实验室,北京 100081)
引 言
作为小行星的重要存在形式,双体小行星在近地小行星、主带小行星与特洛伊小行星中都已被观测到[1]。在近地小行星中,双体小行星的数量约占到其总数的15±4%[2-3]。由于双体小行星系统中天体间所具有的独特运动特性可为研究行星系统的演化提供重要线索,因而成为目前小行星探测的热点目标。双体小行星模型的不确定性及其附近复杂多变的动力学环境对双体小行星探测任务的设计提出了挑战。
近年来双体小行星的稳定特性及其附近复杂的轨道动力学问题引起了学者们的广泛关注。Scheeres[4]基于全二体模型在双体小行星能量与角动量守恒条件下,研究了双体小行星系统旋转运动与平移运动中能量与角动量的转换关系,并给出了双体小行星系统Hill稳定性准则和发生碰撞的条件。基于球和椭球构成的双体小行星系统,Scheeres提出了评估平衡状态下能量稳定性与谱稳定性的方法[5]。Bellerose 等基于椭球-球构成的全二体问题[6-7],研究了相对平衡状态与稳定性问题,推导了稳定性的解析判据,并针对不同构型下的双体小行星系统求解出了稳定区域,研究发现:与限制性三体问题中的稳定区域相比,椭球体-球体系统的稳定范围更小[8]。
本文在前人研究的基础上,通过将椭球体与球体模型拓展至双椭球体模型构成的全二体问题,研究了双体小行星系统的平衡态及稳定性,并分析了不同物理参数对双体小行星平衡态稳定性的影响,将为未来小行星探测提供理论基础。
1 双体小行星动力学与运动方程
1.1 全二体问题
全二体问题研究两个主天体在考虑形状因素以及质量分布的情况下,受相互引力作用而进行的运动,且运动被限制在一个平面内,如图1所示。其中,O点为系统的质心,P1和P2为构成双体小行星系统的两个形状任意、质量分别为M1与M2的主天体。在该双体小行星系统中,分别引入惯性坐标系OXYZ与旋转坐标系Oxyz。惯性坐标系OXYZ的坐标原点为双体小行星系统质心O,X轴指向惯性空间的固定方向,Z轴指向主天体轨道运动的角动量方向,X、Y、Z轴构成右手坐标系。旋转坐标系Oxyz的坐标原点为系统质心O,x轴由主天体P1质心指向主天体P2质心,z轴指向主天体轨道运动的角动量方向,x、y、z构成右手坐标系。此外,分别以小行星的质心为原点建立小行星本体坐标系,选取本体系的xi、yi和zi(i=1,2)轴与小行星主轴方向一致,其中zi轴垂直于轨道面[9]。假设双体小行星系统质心O的运动相对于小行星间的相对运动可忽略,且小行星仅围绕惯性主轴进行自旋,因此,双体小行星间的相对运动可简化为用参数r,ϕi(i=1,2),θ表示的四自由度问题,其中r为两小行星质心间的距离,ϕi(i=1,2)为小行星本体系xi(i=1,2)轴与小行星质心连线的夹角,θ为质心连线相对于惯性系的旋转角度。
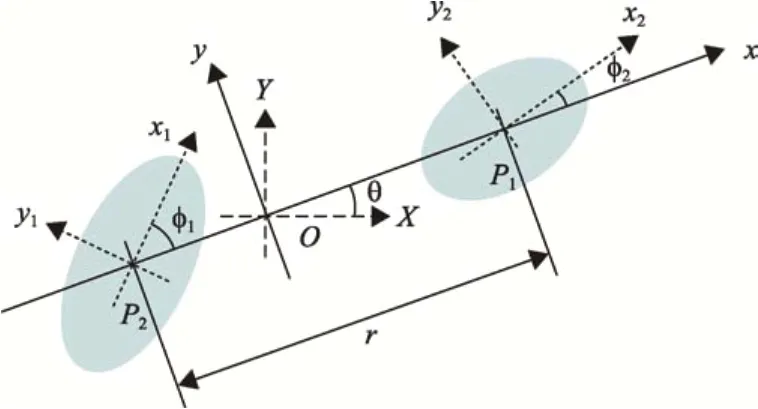
图1 平面全二体问题示意图Fig.1 Planar full two-body problem
1.2 双体小行星系统势能与动能
对于空间全二体问题,惯性系中双体小行星系统的势能为[5]
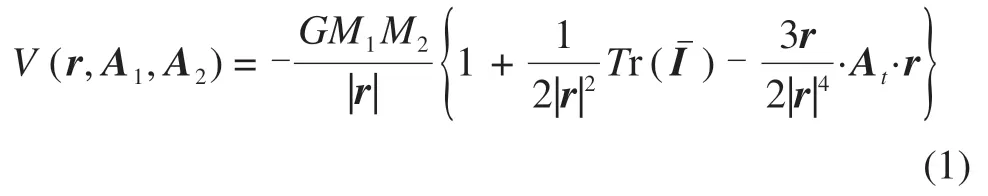
方程(1)给出了将惯性矩阵展开至二阶形式的系统势能。其中:Tr 表示矩阵的迹;为两个小天体质心在惯性系中的相对位置矢量;1,2)为单位化后的惯性矩阵,Mi(i=1,2)为两个小天体的质量;Ai(i=1,2)为由惯性坐标系转换至小天体本体系的旋转矩阵。对于椭球体模型,假设质量均匀分布且椭球体的半长轴分别为αi>βi>γi(i=1,2),则绕主轴的惯性矩可以表示为
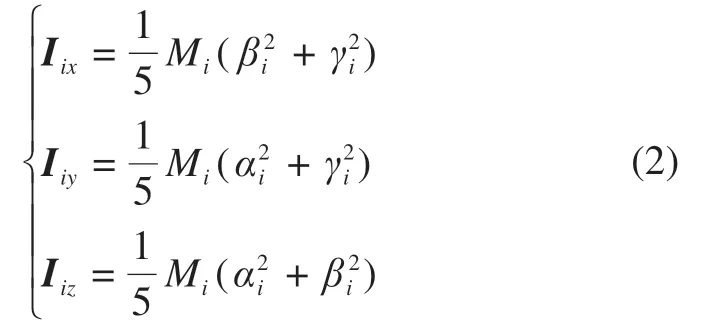
根据系统动能的一般性表达形式,在惯性系OXYZ中可以推导得到双体小行星系统的动能,在假设主天体的旋转仅围绕主惯性矩发生的前提下,系统动能在旋转坐标系下的表达式为

系统的能量可以表示为E=T+V。
1.3 双体小行星系统运动方程
对于双体小行星系统等经典物理系统,定义拉格朗日量L为系统动能与系统势能之差,即

选取两主天体质心间的相对距离r、双体小行星系统角速度以及主天体相对于旋转坐标系的旋转角度ϕi用于表示平面全二体问题中的运动方程。
对于q=[r,θ,ϕ1,ϕ2],根据拉格朗日方程∂L/∂qi=可得双体小行星系统的运动方程为

2 双椭球体系统平衡态与稳定性分析
2.1 双椭球体系统平衡态的状态约束
在求解双体小行星系统平衡态对应的约束方程时,角动量是其中的一个关键参数。分析式(1)与式(3)中的双体小行星系统动能表达式与势能表达式可发现,系统势能与动能的值与双体小行星系统旋转角度θ无关,即双体小行星系统角动量守恒,角动量K的表达式为
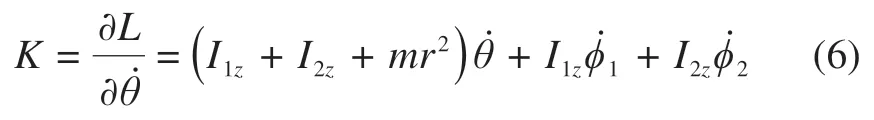
求解双体小行星系统的平衡状态通常将全二体问题运动学方程中关于时间求导数的变量设为零,可求解平衡状态所满足的约束。因此双体小行星系统处于平衡状态的条件为,系统能量E=T+V需满足对各变量求偏导的值均为零。
由于式(1)的势能表达式仅适用于平面全二体问题,因此系统的能量表达式仅适用于平面全二体问题。平面全二体问题的平衡态需满足的约束为
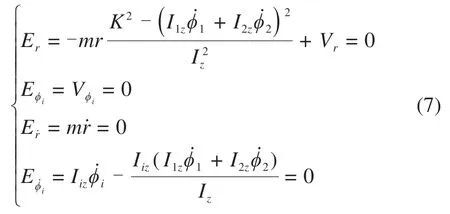
通过式(6)中的4个约束可以确定双体小行星系统平衡状态应满足的3个约束方程为
条件③:Er=0。
本文仅考虑ϕ1=ϕ2=0 的条件下,双体小行星系统的相对运动情况。此时相对平衡态下对应的双体小行星系统角动量平方的值K02与系统能量的大小E0可以分别从式(6)计算得出。
2.2 双椭球体系统平衡态稳定性的分析
在进行双体小行星系统平衡态稳定性分析之前,首先需要引入系统零速度状态的概念,也即两天体相对运动为零时状态变量构成的等式约束。将相对平衡状态r0处的双体小行星系统能量E0与角动量的平方K02带入零速度状态公式,且将平衡状态对应的距离r0作为参数,可以获得双体小行星系统运动可达范围的控制方程。由零速度状态公式推导得到的控制方程为
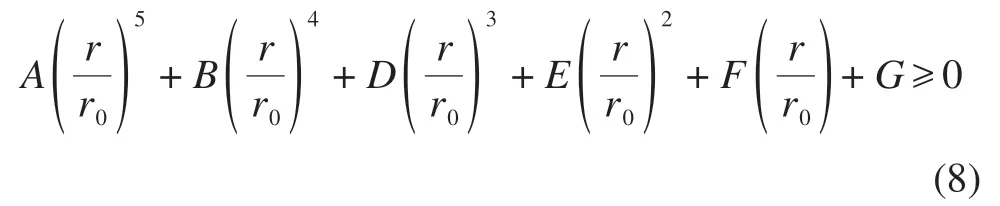
其中,A~G为该五次方程的各阶系数,受小行星质量分布以及平衡状态时两小行星的距离r0的影响。计算验证式(7)的五次方程有二重根r=r0,故可因式分解得到简化的控制方程为
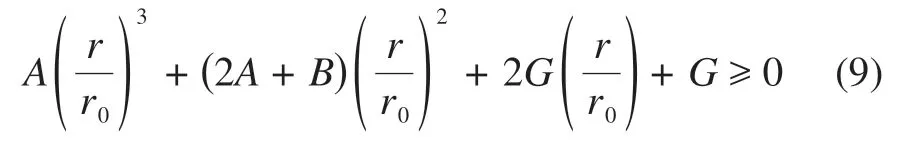
利用劳斯-赫尔维茨判据可得结论:当式(8)中A> 0 时,该方程的根均分布在复平面的左半平面;当A<0 时该方程在复平面的右半平面有一个根,即存在一个正实根。对该三次不等式进行讨论研究,可获得双体小行星系统平衡态稳定性的3种情况:①运动可达范围无上界的不稳定平衡态;②运动可达范围有上界的不稳定平衡态;③稳定的平衡态。
由于平衡态的稳定性本质上关注的是能量稳定性与Hill 稳定性。能量稳定性为一类基础的稳定性类型,决定了系统能否通过能量耗散的方式达到能量较低的状态。双体小行星系统具有能量稳定性意味着该双体小行星系统已达到在给定角动量下能量最低的构型状态。Hill稳定性描述双体小行星系统在相互引力作用下是否具有发生逃逸能力的稳定性,与能量稳定性相比,Hill稳定性研究对象不是平衡状态附近的运动,而是关注双体小行星系统运动的绝对界限。所以以上3 种平衡态稳定性根据其参数特性又可归结为:①Hill 不稳定平衡态;②Hill 稳定、能量不稳定平衡态;③能量稳定平衡态。下面对这3类稳定平衡态分别进行分析。
1)Hill不稳定平衡态
A>0 时,不等式的根均分布于复平面的左半平面,则式(8)中控制方程始终成立,即r的取值范围没有约束,r的取值范围无上界,对应的双体小行星系统在受扰动的情况下可发生逃逸,且r0处对应的自由能始终为正。
A=0时,若2A+B≠0,通过推导分析可知简化后控制不等式始终成立。若2A+B=0,则三次不等式可以简化为2Gr/r0+G≥0,显然控制不等式同样恒成立。
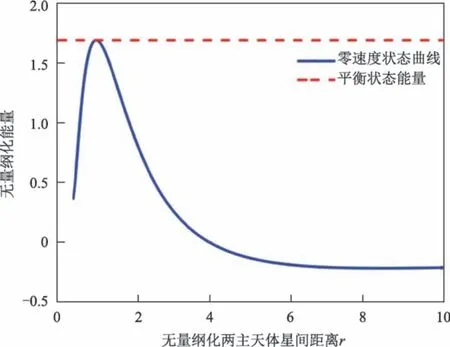
图2 运动可达范围无上界的不稳定平衡态Fig.2 Unstable equilibrium,the motion is allowable on all parts of the curve beneath the equilibrium energy
由以上分析可知,当A>0与A=0时相应的控制方程始终成立,即对应的双体小行星系统在受扰动的情况下可发生逃逸,运动范围r无上界,该情况为运动可达范围无上界的不稳定平衡态。图2所示为系统能量与相对距离的关系,平衡状态位于r/r0=1,运动可达区域为位于平衡状态能量E0之下且零能量曲面之上对应的r的取值范围。
2)Hill稳定、能量不稳定平衡态
在A<0 的情况下,控制方程有一实数根均分布于复平面的右半平面,其余两根分布在复平面的左半平面。假设控制方程的正实根为X,若X> 1 即r >r0,此时r有上界M,且上界M=Xr0应满足M>r0。如果对平衡态r/r0=1处的双体小行星系统施加扰动,则运动可达区域可能达到上界M,即双体小行星系统内两个主天体的相对距离的值可能在r0和M之间变动,运动可达区域为位于平衡状态能量之下的曲线部分对应的距离。在该情况下,r/r0=1处的双体小行星系统的系统总能量为负值,但为不稳定状态。双体小行星系统能量与相对距离的关系如图3所示。
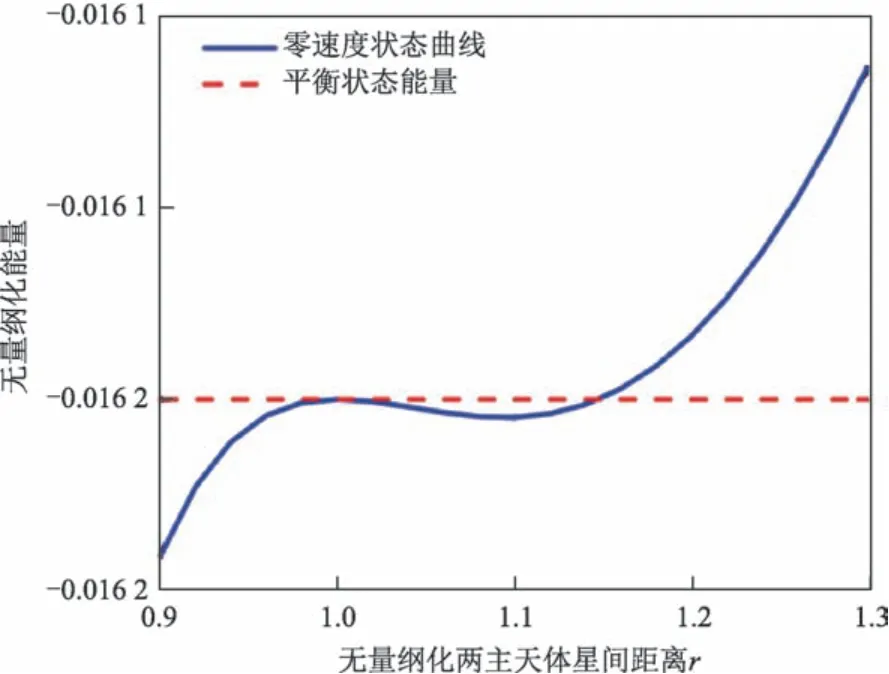
图3 双椭球体系统下运动受限的平衡态Fig.3 Equilibrium with limited movement in the double ellipsoid system
3)能量稳定平衡态
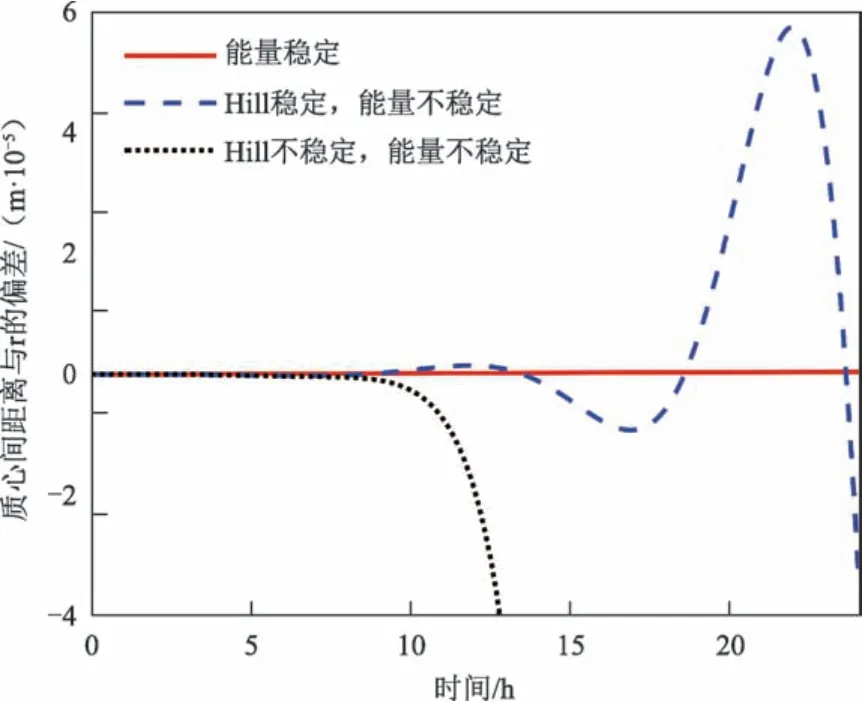
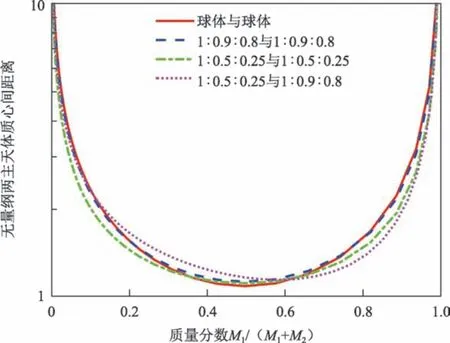
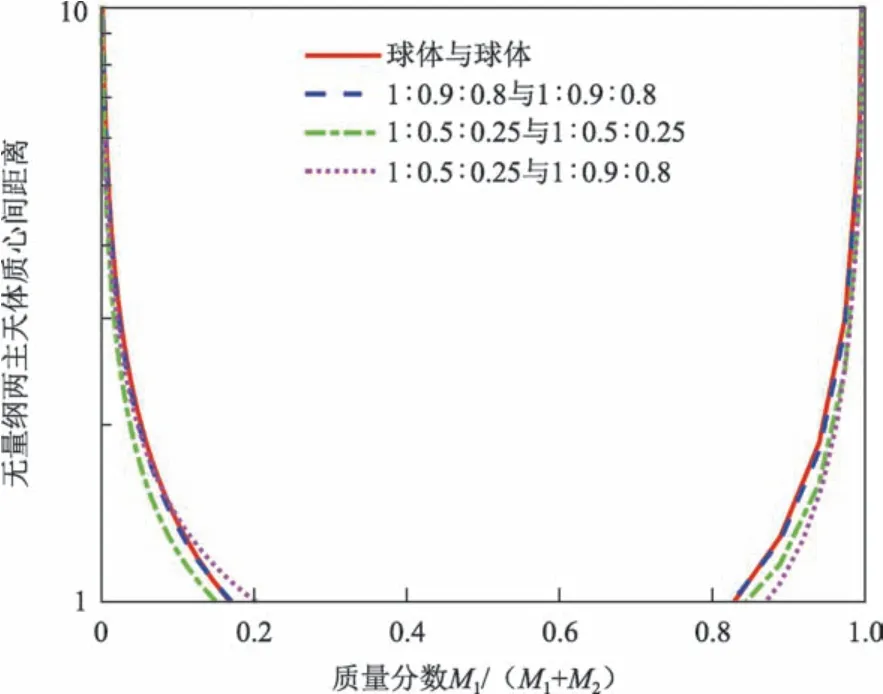
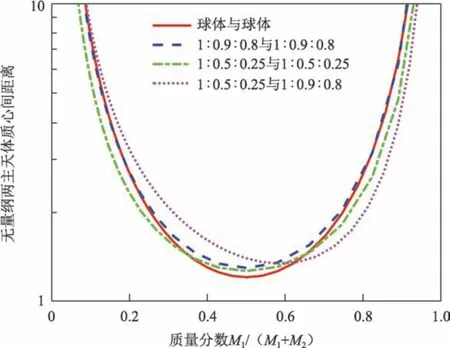
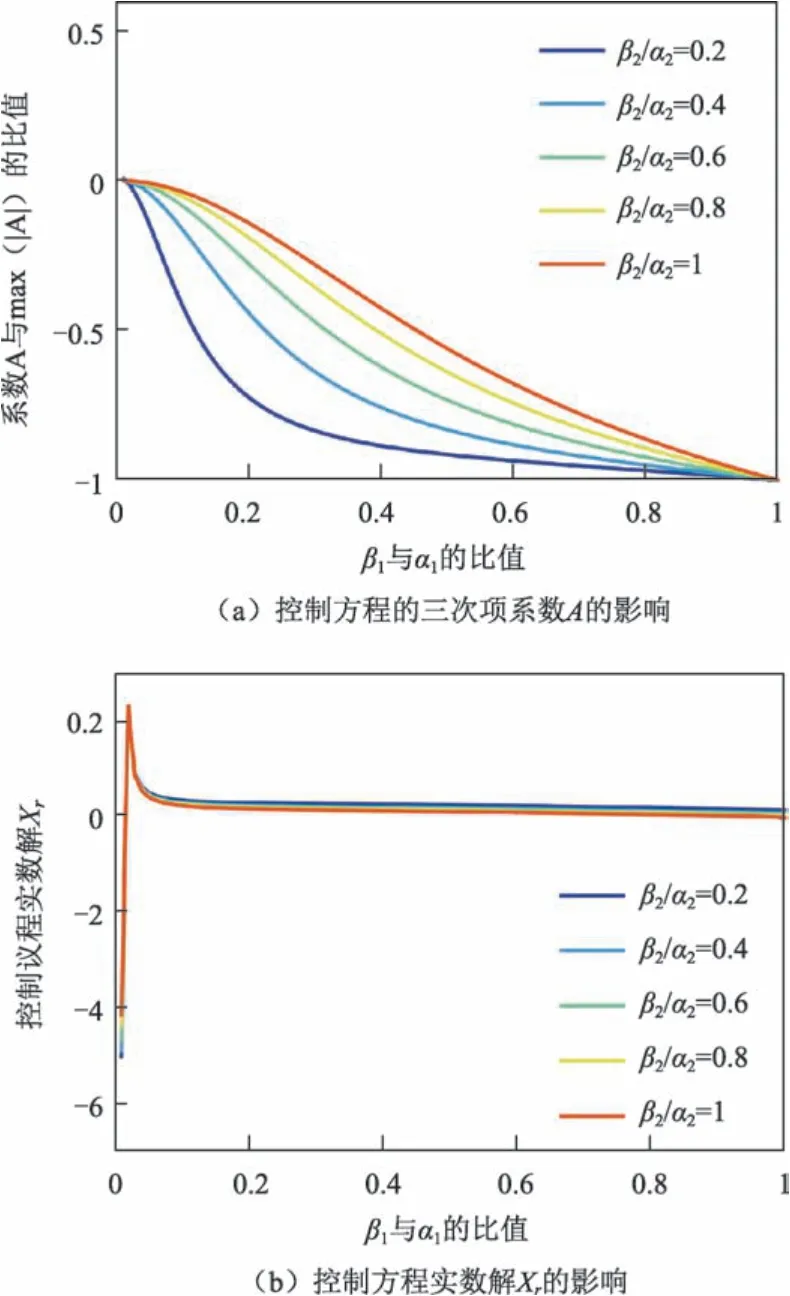
在A< 0 且X≤ 1 即r 图4 双椭球体系统能量最小的平衡态Fig.4 Minimal energy equilibrium in the double ellipsoid system 基于上述关于双体小行星系统平衡态稳定性的结论,研究双体小行星系统平衡态受小行星形状参数、质量分数以及双体小行星系统平衡态时小行星间相对距离等物理参数的影响。 假设小行星Pi为密度均匀一致的双椭球体模型,Pi的椭球体三轴满足αi>βi>γi。根据2.2小节中对双体小行星系统平衡状态稳定性的分类,分别选取形状参数一致的双体小行星系统,并通过调整双体小行星主天体的构型与质心间距离,分别获得3种不同稳定性情况的系统平衡状态。各系统主天体形状参数如表1所示。 表1 3种不同稳定性情况参数选取Table 1 Parameters for three different kinds of equilibrium m 随后对主天体P2质心沿径向施加5 N·s 的冲量,并以施加冲量后的双体小行星系统状态参数为状态初值,依照第2节中提供的双体小行星系统运动方程沿时间正向递推,从而研究双体小行星受到小扰动后的运动变化。递推时长选取为25 h。 图5为分别针对具有能量稳定性、Hill 稳定且能量不稳定性、Hill不稳定性的平衡状态双体小行星系统,施加小扰动力后主天体质心间的运动变化规律。由仿真结果可知,对于处于平衡状态的双体小行星系统受到扰动后主天体质心间的距离变化可依据不同的稳定特性分为3 类。针对能量稳定系统施加小扰动时,双体小行星系统主天体质心间距离具有保持原平衡状态不改变的特性。在平衡状态的双体小行星系统具有Hill稳定的情况中,施加小扰动使得两个主天体质心间的相对距离在一定范围内改变,系统呈现有界的相对运动。对于平衡状态下Hill不稳定的双体小行星系统,施加极其微小的扰动即可使系统主天体质心间的相对距离达到无穷远,即发生逃逸。 图5 能量稳定、Hill稳定但能量不稳定、Hill不稳定双体小行星系统质心距离变化Fig.5 Centroid distance of energy stable,Hill stable but energy unstable,Hill unstable binary asteroid systems 由2.2节中关于能量稳定性与Hill稳定性的结论,绘制质量分数的值在[0,1]之间变化的不同椭球体形状下曲线。图6~8 中的距离长度已相对于两椭球体的半长轴之和α1+α2单位化。将双球体模型的曲线与不同形状参数下双椭球体的曲线结果对比,显示出不同形状对应结果的差异。 图6~8 展示了考虑两天体形状为椭球时,因形状参数的改变而产生的能量稳定极限、Hill稳定极限以及角动量相同时对应的共轭解的变化。由图6~8可知,在改变形状参数的过程中稳定性界限的特性未发生质的改变,比如对于Hill稳定性的极限,存在某一部分使得对于任意天体质心间距离,双体小行星系统均具有Hill稳定性,对于能量稳定性则不存在这种情况;Hill稳定极限对应的两天体间距离始终小于能量稳定极限对应的距离。微小的椭球率可一定程度改变系统的稳定性极限,且两主天体三轴比例不同的情况会使得对应的能量稳定性极限、Hill稳定性极限以及共轭解的曲线不再具有对称性。下面分析小行星形状参数变化对双体小行星系统平衡态稳定性的影响。假设主天体形状参数满足βi=γi,选取小行星归一化后的的长半轴为α1=6,α2=4,两个小行星质心间的初始平衡态距离为r*=10。 图6 不同形状参数天体的能量稳定质心间距离极限随质量分数的变化Fig.6 Centroid distance limit of energy stable system for a range of different shape bodies 图7 不同形状参数天体Hill稳定质心间距离极限随质量分数的变化Fig.7 Centroid distance limit of Hill stable system for a range of different shape bodies 图8 与接触系统具有相同角动量的不同形状天体的共轭解随质量分数的变化Fig.8 Conjugate stable solutions for a range of different shape bodies.The conjugate solution has the same angular momentum as the solution for a touching system 图9给出了控制方程的三次项系数A与控制方程实数解Xr的变化曲线。由图9可知,每一条曲线均具有相似的变化趋势,即当主天体P1短半轴与长半轴的比值β1/α1极小时,控制方程三次项系数A>0,此时双体小行星系统处于可能发生逃逸的不稳定状态;随着β1/α1略微增大,存在小部分区间可满足A<0且Xr>1,该情况下双体小行星系统运动可达范围具有上界M=Xr r*,为能量不稳定的相对平衡状态;主星形状参数β1/α1继续增大,双体小行星系统的结果为A<0且Xr<1,即平衡状态能量稳定。而针对不同取值的β2/α2可发现,主天体P2短半轴与长半轴的比值的增大将使得双体小行星系统达到稳定状态所需的小行星P1的形状参数比例β1/α1更小。 下面分析不同小行星质量分数对双体小行星系统平衡态稳定性的影响。令主天体的三轴比例满足1:0.75:0.5,选取小行星P2的长半轴为α2=1,两个小行星质心间的距离为r*=10,给出控制方程的三次项系数A与控制方程实数解Xr的变化曲线如图10所示。图中变化曲线与图9(b)中变化趋势相近,出现该现象的原因为在假设密度相同的条件下,β1/α1比值的增加将导致质量分数的增大。并且在质量分数极大时,即小行星P1的质量M1远大于M2时,双体小行星平衡状态对应的A与Xr增大,双体小行星系统开始由能量稳定的相对平衡状态向Hill 稳定且能量不稳定状态转变。 图9 β1/α1与β2/α2对控制方程的三次项系数A与控制方程实数解Xr的影响Fig.9 Effect of β1/α1 and β2/α2 on oefficient A and real solution Xr in the control equation 图10 质量分数对双体小行星系统平衡态稳定性的影响Fig.10 Influence of the mass ratio on the stability of equilibrium 最后分析小行星间相对距离变化对双体小行星系统平衡态稳定性的影响。假设两个小行星具有相同的形状参数,选取小行星的长半轴α1=α2=1,为保证两个小行星初始状态不为碰撞状态,质心间的距离取值需r*>α1+α2,即在[2,10]的区间内改变双体小行星系统的质心距离。 控制方程的三次项系数A与控制方程实数解Xr的随r*变化的曲线如图11所示。由图11可知,随着双星间距离的增加,A为负值且持续减小,Xr始终为小于1的正数,即双体小行星系统的相对平衡状态将在r*增大的过程中始终保持稳定状态。 图11 小行星间距离r0对双体小行星系统平衡态稳定性的影响Fig.11 Influence of the centroid distance on the stability of equilibrium 本文研究了双体小行星系统在考虑形状参数与质量分布的情况下,在相互引力作用运动的平衡态与稳定性问题。文中基于双椭球构成的全二体模型从分析双体小行星系统的运动可达范围的角度给出了确定双体小行星系统平衡状态的稳定性的方法。研究发现小行星形状参数β1/α1的增大可使得双体小行星系统由具有逃逸潜能的不稳定平衡态,经历运动范围存在上界的平衡状态,最终转变为稳定的平衡状态;β2/α2增大将使得双体小行星系统最终达到稳定状态对应的β1/α1临界值更小。双体小行星系统质量分数M1/(M1+M2)的增大对稳定性的影响与形状参数产生的影响类似,但在M1>>M2时系统由稳定平衡状态趋近于有上界的不稳定状态。系统平衡态时小行星质心间的距离r0的改变不会对系统的稳定性产生质的影响。这些研究结论对于未来双体小行星附近探测器的运动研究具有重要的理论指导意义。
3 双体小行星系统物理参数对平衡态稳定性影响分析



4 结 论

