碎石堆构造小行星表面地形分析与仿真验证

王亚林，刘 鹏，吴辉阳，黎 衡，赵 巍

（1.哈尔滨工业大学计算机科学与技术学院，哈尔滨 150001；2.中国人民解放军63861部队，白城 137001）

引 言

小行星是太阳系的重要组成部分，对地球环境的演化和人类的生存都有重大影响。一方面，小行星保存了较多太阳系早期的形态、特性，可以用来研究太阳系的形成和演变过程；另一方面，经不懈努力所获得的小天体知识将有助于人类进一步对太阳系深度探索，如天体表面取样用于评估小天体蕴含矿藏的可利用性等。

在过去的20年里，随着航天技术的发展，小行星探测任务从地基、空基望远镜观测逐渐延伸到航天器的近距离观测，比如2000年，NASA 的近地小行星交会（Near Earth Asteroid RendezvoHs，NEAR）探测器成功环绕近地小行星Eros（433），并最终降落在Eros 的表面；2005年日本“隼鸟号”（Hayabusa）成功在近地小行星Itokawa（25143）上进行了一触即走式着陆，采集了小行星表面物质；2012年12月13日，我国的“嫦娥2 号”飞船近距离飞越小行星Toutatis（4179）并获取了清晰的遥感图像。

目前多个国家制定了明确的小行星探测规划，如日本正在进行的“隼鸟2号”任务（2014年12月3日发射），目标为近地小行星1999JU3（162173）；美国正在开展的 OSIRIS-REx 任务 （2016年 9月 8日发射），目标为小行星1999RQ36（101955）；欧洲航天局（European Space Agency，ESA）MarcoPolo-R 任务，目标为近地小行星2008EV5。

深空探测任务既需要充分掌握某潜在目标的轨道、动力学、引力场等特性，也需要对目标小天体的着陆取样返回系列任务提供可靠的技术保障。小天体表面安全着陆是对探测器的着陆导航机构和着陆导航策略的极大考验。2005年11月25日日本的“隼鸟号”子飞船密涅瓦在登陆过程中迷失失联；2014年11月22日ESA“罗塞塔号”的“菲莱”着陆器在登陆彗星67P/Churyumov-Gerasimenko 时反弹并进入了一个光线昏暗的巨石堆/碎石堆区域。

对于尺寸很小（约1 km）的碎石堆小行星而言，其引力场低、逃逸速度低（约10-2~10-1m/s），对此类小天体开展着陆段导航和表面操作（如锚定、取样、返回等）的实时性、安全性和精度有高要求。视觉辅助的地形相对导航可以提高探测器着陆的成功率。因此，需要构建一个高精度的小行星地形模型用于着陆机构安全性可靠性验证和地形相对导航的算法验证。

目前研究人员对行星、小天体表面地形的仿真验证平台的构建方法主要有：Parkes 等人使用PANGU对星体表面进行模拟，着重做较大行星表面仿真[1]；Sánchez等使用软球离散单元法（Soft-Sphere Discrete Element Method，SSDEM）来模拟碎石堆小行星的旋转重塑，重点分析组成小行星的碎石之间的作用力[2]；Van Wal 提出了一种高保真的小天体表面着陆仿真方法，重点在于着陆器与地形之间的碰撞分析[3]。这些方法多是建立较为粗糙的整体地形模型，没有构建出局部高精度地形。

本文根据小天体表面操作执行机构和着陆段导航方法验证需求，选择并仿真生成5 种典型局部地形。在不考虑小行星表面引力、热惯量、自转周期等物理特性的条件下，通过计算机仿真的手段评估仿真参数对地形生成结果的影响以及与真实地形间的相似程度，为机构及方法验证提供数据支持。

1 小行星地形研究

1.1 地形特性

研究表明，小行星是由重力和凝聚力结合在一起的碎石堆[4-5]，其表面覆盖有风化层。风化层主要由厘米级至数米级大小不一的石块构成。Miyamoto等[6]通过研究小行星Itokawa 高分辨率的图像发现这些石块在干燥、真空和微重力的环境下，由于振动引发了整个小行星的颗粒化过程；由于Itokawa的体积较小，这种颗粒化的过程成为了其主要的表面重构过程，这也意味着该过程很有可能会发生在其它小行星上。小行星的体积越小，极低的重力允许相对较大的细颗粒得以逃脱，这些细颗粒可能是由微型陨石或者电离引起的，当这些细颗粒被运输漂散，地表就会腐蚀或“收缩”，由此产生了所谓的“巴西坚果效应”[7]，即体积比较大的颗粒会上升到表层，而较小的颗粒会沉降到底部；并最终在小行星表面形成了，如图1（a）所示的地形[8]。

图1 小行星表面石块图片示例Fig.1 Image illustration of real boulders，cobbles and dust on asteroid surface

较小的碎石通常具有更高的流动性，因为它们有较低的摩擦，移动它们所需的振动的振幅也较小。碎石移动性的不同导致了它们的分离，进而导致了灰尘池塘（光滑地形）的形成，如图1（b）所示，这也是光滑地形和粗糙地形之间的边界如此明显的原因。

1.2 石块特性

对碎石堆小行星表面石块的进一步研究表明：小行星表面的石块尺寸概率密度函数PDFX(d)服从以下幂律分布

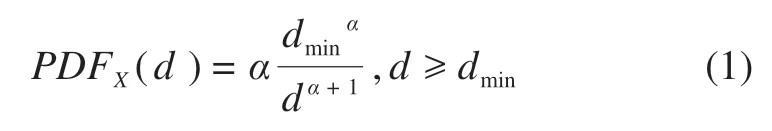
其中：α>0被称作幂指数；dmin是石块的最小尺寸。

显然，对于不同地形区域其幂指数的值是不同的。通过对小行星Itokawa 表面石块数据的研究Michikami 等得出结论[9]，Itokawa 表面的粗糙区域幂指数为2.8±0.1，光滑区域幂指数为3.2±0.1。Mazrouei指出[10]，在Itokawa表面直径小于15 m的石块的幂指数是2.1±0.1，进而在最新的成果[11]中给出修正的幂指数为3.1～3.5，与其他学者的成果给出的2～4的范围相当。

另一方面，选择石块的最小尺寸dmin可以避免出现当dmin趋近于0 时，PDF趋近于1 的畸形情况；同时，为了避免生成超大石块，定义石块的最大尺寸dmax。假设y是[0,1]之间的均匀分布，那么可以由以下公式得出服从幂律分布的d

小行星表面的石块数量服从下述公式

其中：k0是单位面积上半径大于d0的石块数量；k是单位面积上半径大于dmin的石块数量。根据Mazrouei的研究结果[10]，小行星Itokawa 单位面积上半径大于d0=2.5 m的石块数量为k0=2.05×10-3m-2。

在对Itokawa 的石块外形分析中[9]，指出石块的长宽高比例大致为或简记为a∶b∶c=1∶0.7∶0.5。

2 小行星地形模拟生成方法

2.1 地形模型

在给定了数目且服从幂律分布的石块以后，还不能确定这些石块在小行星表面的分布，原因是由公式（3）计算出的单位面积上大于某一尺寸的石块数量是基于整个小行星的平均数据。但是大致的分布趋势可以确定如下[12]：在重力势较高的地方，均为厘米级大小的碎石铺满的“池塘”；而在重力势较低的地方，大多是较大块的石块。为了进一步区分不同引力场位置的局部地形，本文按照地形区域内石块数量及分布情况将地形分为以下5类：

1）灰尘池塘：只含有碎石；

2）石块密布区：含有任意大小的石块；

3）石块区和灰尘池塘的过渡区域；

4）灰尘池塘中散布石块；

5）石块密布区中有小块灰尘池塘。

图2 5种典型地形的真实示例（图片来源于Itokawa小行星，编号依次为st_2563537820、st_2530297837、st_2539423137、st_2563511720、st_2532629277）Fig.2 Image illustration of five typical real terrains from Itokawa asteroid with image label st_2563537820，st_2530297837，st_2539423137，st_2563511720，and st_2532629277

2.2 石块模型

根据石块的尺寸大小，将其分为3 种：碎石（dust）半径0.02～0.05 m；鹅卵石（cobble）半径0.05～0.5 m；巨石（boulder）半径0.5 m以上。

由于石块确切形状既不是立方体也不是球体，或者其它立方体，因此石块的模型必须有足够的复杂性，同时必须有足够的简单性以供大范围的模拟，选择随机形变的二十面体来表征石块。石块按照以下步骤生成：

1）生成一个直径为d的正二十面体Stone=[Point,Face]；

2）对二十面体的12 个顶点进行最大偏差为d/4的随机伸缩Point=Point+StretchMatrix

3）对二十面体进行a∶b∶c=1∶0.7∶0.5 的比例缩放Point=Point⋅ReshapeMatrix

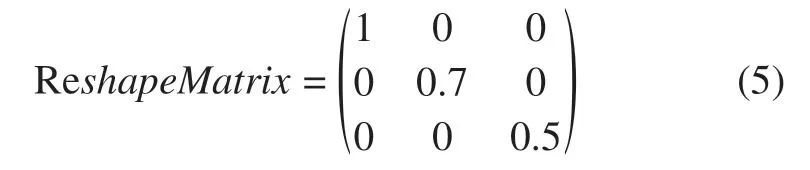
4）在3 个方向上随机选取旋转角度，对石块进行旋Point=Point⋅RotationMatrix

式中α、β、γ是绕X轴、Y轴、Z轴旋转的角度。

图3依次展示了原始、随机形变、比例缩放、随机旋转的石块。

图3 原始、随机形变、比例缩放、随机旋转的石块模型Fig.3 Illustration of regular icosahedron and its random deformation，non-uniform scaling，and random rotating in simulating boulders

2.3 地形生成方法

按照仿真需求，需要生成一个3 m×3 m 大小的仿真着陆区，每像素分辨率为区域边长的千分之一。经计算，一个1 024×1 024像素的图片，每像素分辨率为3 mm 即可满足仿真区域的需求。使用两个1 024×1 024大小的图分别存储每个像素点的高度信息和石块信息。

2.3.1 石块放置方法

仿真地形按照以下步骤生成：

1）在1 024×1 024 的平面上，随机选取位置放置石块并以随机深度下沉，更新高度和石块信息（石块编号），直至平面的铺满度达到某一阈值（例如95%）或者达到石块数目上限；

2）在随机选取位置的过程中，若该位置的石块信息已被更改（初始为0），则再次随机选取位置。此做法能保证石块总是铺在未曾放置石块的位置，直至铺满度达到阈值；

3）石块的详细信息按照编号存储在列表中。

地形I、II、IV 中石块位置的随机选取都服从均匀分布，为了实现地形III中石块到灰尘池塘的过渡，大石块的位置分布不再服从均匀分布，而是服从p(x,y)=a(x+y)-k的概率分布，其中a是归一化因子，k=0.5，即：距离左上角越近，大石块的分布概率越高；而在地形V 中设定了一个均值为d/3、方差为d/6 的圆形的区域，当大石块落入这一区域时，再次随机生成一个位置。

石块放置时，将石块坐标系的原点放置到选定的位置上，并将其随机下沉，最后再将石块的各点坐标由石块本体坐标系o-xyz转到为地形坐标系O-XYZ下，如图4所示。

图4 地形坐标系与石块本体坐标系Fig.4 Relation between terrain coordinate system and boulder’s body-fixed coordinate system

2.3.2 石块高度更新方法

为了更新地面高程信息，需要得到石块每个面上所有的XY坐标值为整数值（代表一个像素点位置）的点(x,y,z)，称为像素点。三维空间的任意平面可以由Kx+My+Lz+N=0 表示，对于一个石块的某一个确定的面，只要确定x,y的值就可以根据平面公式计算出z值，则只需寻找所需的x,y值，寻找一个石块一个面上所有的像素点通过以下步骤完成：

1）将石块的面ABC沿A'B'轴方向投影到XOY平面上得到三角形A'B'C'，三角形A'B'C'边上和内部的所有XY坐标为整值的点即为所求点，如图5（a）；

2）计算三角形A'B'C'的外切矩形，将其中所有XY坐标为整数值的点作为候选点；

3）要得到三角形A'B'C'所有边上的点，因为采用像素的形式，XY坐标只能是离散整数值，例如构成边A'B'的像素点不严格满足其直线方程K'x+M'y+L'=0,故此处采用计算机图形学中的直线扫描转换方法之一：Bresenham 画线算法（Bresenham's line algorithm）来确定构成该条线段的像素点，如图5（b）；

4）要得到三角形内部的点，使用叉乘法判断：平面内一点P在三角形A'B'C'内部当且仅当三组向量方向相同。对所有候选点进行如上检测，如图5（c）；

5）根据所有已经获得的(x,y)，计算出其对应在平面ABC的坐标(x,y,z)，返回所有的(x,y,z)。

2.4 算法流程

总结2.1~2.3 中的小行星地形模拟生成方法，得到算法的流程图，如图6所示。

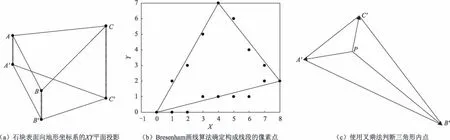
图5 地形高度更新方法示意图Fig.5 Main steps of terrain altitude updating

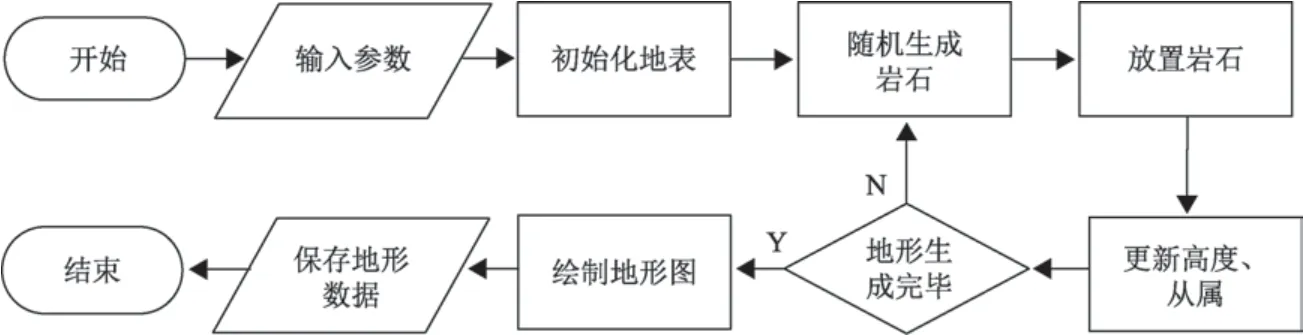
图6 算法流程图Fig.6 Flowchart of asteroids topography generating algorithm

3 实验结果

在windows10 平台下按照第3 部分的仿真方法，利用matlab实现了仿真算法，并对仿真关键参数：幂律指数α进行了研究。由第2 部分小行星地形知识，学者得出的幂律指数范围为2~4，但是结果来源于直径5 m 以上[12]或直径15 m 以下的石块[11]的统计结果，本文的地形仿真中石块尺寸在直径1 m以下，故扩大了幂律指数的取值区间，对幂律指数α按2~5的范围进行仿真验证。其中图7(a)α为 4.8，7(d)α为 4.2，7(b)、7(c)及7(e)的α均为2.8。

由图7(a)(d)(b)可知随着幂律指数α变小，仿真地形上大尺寸的石块随之增多，分别对应着地形I、II、IV。图7(b)(c)(e)中的幂律指数α均为2.8，大尺寸石块数量大体相同，但由于其不同的放置策略得出了地形II、III、V。

由图8可知，石块尺寸分布直方图大致相同，只是其斜率有所区别，由于坐标系为对数坐标，这表明生成的石块尺寸服从幂律分布。

图7 五种地形示例、仿真结果、地形仿真参数及石块尺寸-频率直方图（对数坐标）Fig.7 Five typical terrains，simulation results，terrain parameters and boulder-size-frequency histogram in log coordinates

4 结 论

本文通过对碎石堆小行星地表及石块特性的研究，建立了地形仿真模型及方法。仿真结果表明该方法生成的仿真地形与实际探测得到的小行星表面局部地形相比一致性较好，可以用于着陆器的着陆机构验证和着陆器着陆导航及视景仿真。