含预紧弹簧碰撞系统的两参数动力学
吕小红, 王继培, 张锦涛
(兰州交通大学 机电工程学院,兰州 730070)
近年来,非光滑动力系统以其在日常生活中的普遍性和在实际工程领域的重要性,引起了诸多学者和工程技术人员的关注。碰撞系统作为非光滑动力系统的典型代表,广泛存在于机械工程领域。由于碰撞、黏滞和擦边等因素引起的非线性和奇异性问题使碰撞系统呈现复杂的动力学行为[1-2],并对系统的使用效率和性能等产生重要的影响。因此,碰撞系统的动力学研究具有重要的工程应用价值。
Floquet理论是研究周期运动稳定性的理论基础。Poincaré映射是非光滑动力系统周期运动分岔研究的主要手段。通过构建Poincaré映射,周期运动的求解可转化为Poincaré映射的不动点问题。因此,碰撞系统周期运动稳定性分析的关键是计算Poincaré映射的Jacobi矩阵的特征值,即Floquet乘子。但是,间隙和约束等非光滑力学因素的存在给碰撞系统Floquet乘子的计算增添了较大的难度。金俐等[3]推导了碰撞系统轨线在定相位面与碰撞面之间切换的局部映射的Jacobi矩阵,构建由四类局部映射复合而成的Poincaré映射,得到Floquet乘子计算的解析方法和数值方法。徐慧东等[4]推导了弹性碰撞系统在非光滑界面处的跳跃矩阵, 然后与各子区域的连续基解矩阵合成,得到Poincaré映射的Jacobi矩阵。擦边接触对碰撞系统周期吸引子的演化及常规分岔的产生与中断具有重要的影响。Yin等[5]推导了描述擦边碰撞的局部零时间不连续映射及其和光滑流映射组成的复合Poincaré映射。打靶法是计算周期吸引子(包括稳定和不稳定)的常用方法。基于Floquet理论和Poincaré映射,结合打靶法和延续法能够系统地探究参数大范围变化时,非光滑动力系统周期吸引子的稳定性与分岔[6-8]。
碰撞系统存在大量的多吸引子共存现象,包括多周期、周期与混沌以及混沌与混沌的共存。此时,系统全局动力学的研究显得至关重要。应用胞映射法可揭示非光滑动力系统共存吸引子的吸引域及其演化过程[9]。当混沌吸引子与其它吸引子共存时,激变是一种常见的全局现象[10-12]。
两参数动力学更能揭示碰撞系统的动力学与系统参数的耦合关系。吕小红等[13-14]应用数值仿真方法研究了两自由度碰撞系统的两参数动力学,揭示了碰撞系统周期吸引子模式的多样性和规律特征及两参数发生域,发现在相邻基本周期运动的两参数转迁过程中存在两种特殊转迁域: 迟滞域和亚谐包含域。由于协同仿真方法不能精确计算分岔点信息和不稳定吸引子,以及对共存吸引子的全局动力学以及混沌转迁考虑较少,因此,一些吸引子信息可能被隐藏,迟滞域和亚谐包含域的形成机理及其内部的动力学没有被完全揭示。本文结合Runge-Kutta法、打靶法、延续法和胞映射法研究含预紧弹簧碰撞系统在两参数平面的稳定性与演化规律,试图发现一些易隐藏的由不连续性诱导的分岔行为,讨论不稳定吸引子在相邻吸引子转迁过程中的重要作用,揭示迟滞域和亚谐包含域的形成机理。
1 力学模型

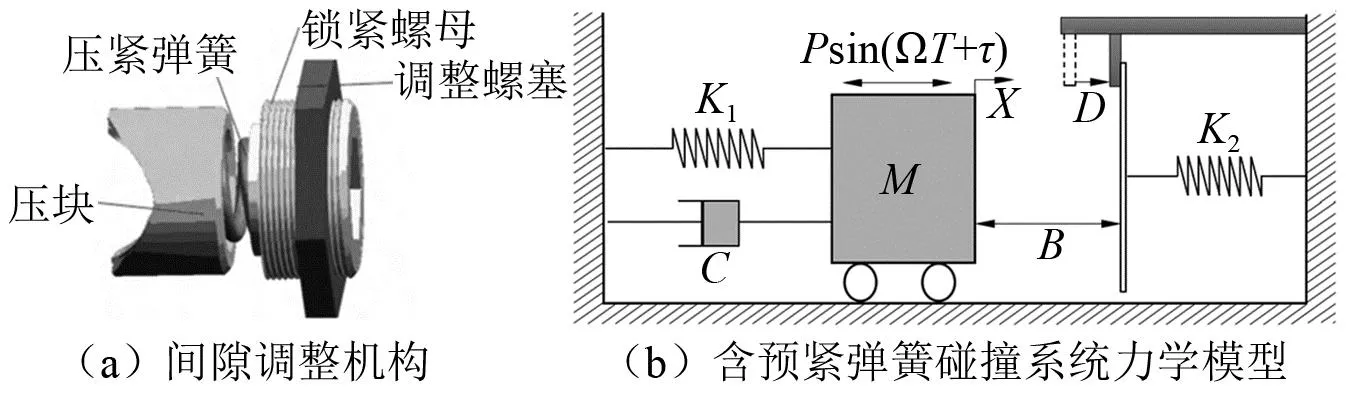
图1 含预紧弹簧机构和力学模型
(1)
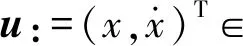
(2)
2 数值方法
碰撞系统周期吸引子分岔分析的常用数值方法有两种:应用Runge-Kutta法直接求解系统运动微分方程的数值仿真,以及Runge-Kutta法、打靶法和延续法结合的数值延拓。数值仿真方法只能得到稳定周期解和混沌解,而不稳定周期吸引子在分岔和混沌转迁中具有很重要的作用。因此,我们借助基于Poincaré映射的打靶法求解系统的不稳定周期吸引子以帮助解释分岔与混沌转迁。
碰撞系统的周期吸引子模式具有多样性和复杂性特征,因此对于预先给定的正整数n, 取Π0={(u,t)∈2×S|mod(t,2nπ/ω)=0}为映射截面构建Poincaré映射P:Π0→Π0。由于式(2)为分段光滑系统,定义系统在各子区域的光滑流映射
Pi:Πi0→Πi1,ui0ui1,i=1,2
(3)
式中:ui为子区域Gi中的状态变量;ui0和ui1分别为光滑流的起点和终点,对应的时刻分别为ti0和ti1。映射Pi的Jacobi矩阵DPi为
(4)
DPi可由矩阵微分式(5)联立式(1)借助Runge-Kutta法从ti0到ti1进行数值积分求∂ui(t)/∂ui0的解。
(5)
在t11和t21时刻,系统轨线经非光滑界面在G1和G2区域之间切换。非光滑分界面的法向量hu=[1,0]T,引入不连续映射及其Jacobi矩阵
P12:Π11→Π20,u11u20
(6)
P21:Π21→Π10,u21u10
(7)
(8)
(9)
用n-m表示稳定周期吸引子模式,其中n和m分别表示一个振动周期内的力周期数和轨线进入G2区域的次数。不稳定的n-m吸引子用Un-m区分。由u10点出发的n-m或Un-m吸引子的Poincaré映射及其Jacobi矩阵分别为
(10)
(11)
周期吸引子的边值条件为
u(0)=u(nT)
(12)
式中,T=2π/ω。应用打靶法求解时,边值条件要求Poincaré截面上的初值u0满足
Q(u0)=u(nT;u0)-u(0;u0)=P(u0)-u0=0
(13)
采用Newton-Raphson法构成迭代式
(14)
式中,i为迭代次数。给定u0,然后根据式(14)进行修正,直到满足Q(u0)=‖P(u0)-u0‖<ε(ε为预先给定的小量)时,便得到一个周期n吸引子,所得u0为映射P的不动点。令z:=(b,0)T,δ(u)=‖u-z‖,在数值求解P(u0)过程中,计数轨线进入G2区域的次数m,并计算δ(u)的最小值δ(u)min。因此,得到u0的同时,根据计数的m值及DP(u0)的特征值便可确定吸引子模式及其稳定性。若δ(u)min<ε,则系统轨线存在擦边碰撞,此时的参数值为擦边分岔点。
设分岔参数为v, 应用打靶法求得v=v0时的周期吸引子u0后,希望能利用该吸引子信息求得v1=v0+Δv时的周期吸引子,进而求得参数v大范围变化的分岔曲线。为此需要应用延续法在Poincaré截面上沿切线方向预估v=v1时的初值向量,然后用打靶法修正。预估值为
(15)
式中,Q(v0,u0)=P(v0,u0)-u0, ∂Q(v0,u0)/∂u=DP(v0,u0)-I。∂Q(v0,u0)/∂v可由式(16)以[u0,0]可由式(16)以为初值积分n个力周期T得到。
(16)
为了研究系统的全局动力学,本文首先选择一个初值考察区域H,并对其进行网格划分;然后以每个网格中心点的值作为初值向量,应用打靶法求解周期吸引子及其稳定性。待所有网格中心点考察完毕,便可得到系统的共存吸引子;最后数值延拓每个共存吸引子的分岔演化,应用胞映射法计算吸引域。
3 两参数分岔分析
为了研究系统周期1吸引子的分岔特征,揭示迟滞域和亚谐包含域的形成机理,取参数(1):k=9,ξ=0.08,d=0.1,数值仿真系统在ω-b参数平面(0.1≤ω≤0.8,0.1≤b≤1.3)的动力学响应如图2(a)所示。图2中,各种类型周期吸引子的参数域标注有相应的符号。在图2(a)所示两参数区域内,系统的主要响应为1-m(m≥0)吸引子。在相邻1-m吸引子的临界线上,可观察到若干系统响应为亚谐周期n(n≥2)吸引子及混沌吸引子、可称为亚谐包含域的参数岛。因此,相邻1-m吸引子的参数域之间存在两类特殊转迁域:迟滞域和亚谐包含域。为了方便分析,1-m与1-(m+1)吸引子之间的亚谐包含域用SIRm表示。需要指出,图2(a)仅识别了1-m(m=1, 2, …, 8)吸引子以及SIRm内的周期2和周期3吸引子,其余1-m(m>8)吸引子统一用深灰色表示,亚谐周期n(n>2)及混沌吸引子用浅灰色表示。可见,分岔参数越小,1-m吸引子的m值越大,对应的ω-b区域越窄。1-m(m≥1)吸引子的两参数下边界线表现为具有下降趋势的波浪线。增大ω,波浪线的波长和波高增大,邻近波峰位置的SIRm面积增加。同时,周期吸引子模式逐渐增多以及混沌吸引子的参数域面积增大使得SIRm(m≥2)形状发生改变,动力学行为更加复杂。我们把位于末次波峰位置的结构严重变形的亚谐包含域称为非标准型,其它的称为标准型。标准型和非标准型亚谐包含域用SIRm-S和SIRm-N区分(SIR0和SIR1只有标准型)。图2(b)~图2(d)描述了SIR0-S和SIR2-N内的详细动力学。可见,SIRm内的亚谐周期吸引子模式具有一定的规律性,主要表现为k-(km+1) (k=2, 3, 4, …)以及2-2(m+1)。但是,在SIR2-N内,2-6和混沌吸引子的参数域面积明显增大,以及2-4、3-8和4-12等模式周期吸引子的出现导致相邻1-2与1-3吸引子经SIR2-N的转迁路径更加多样和复杂。由于相邻1-m吸引子经标准型和非标准型亚谐包含域的转迁路径有明显区别,下面以图2(b)和图2(d)所示SIR0-S和SIR2-N为对象进行单参数延拓分析,揭示相邻1-m吸引子的转迁特征以及两类特殊转迁域的形成机理。图2中标有HD的浅色区域为迟滞域。

图2 两参数动力学
3.1 标准型亚谐包含域内的不连续分岔
为了揭示相邻1-m与1-(m+1)吸引子经迟滞域和标准型亚谐包含域转迁的特征规律,应用数值仿真和数值延拓两种方法计算的单参数分岔图如图3所示。图3中,实线表示稳定周期吸引子,虚线表示不稳定周期吸引子。擦边、周期倍化和鞍结分岔点用圆点表示,并分别标注G、P和S。
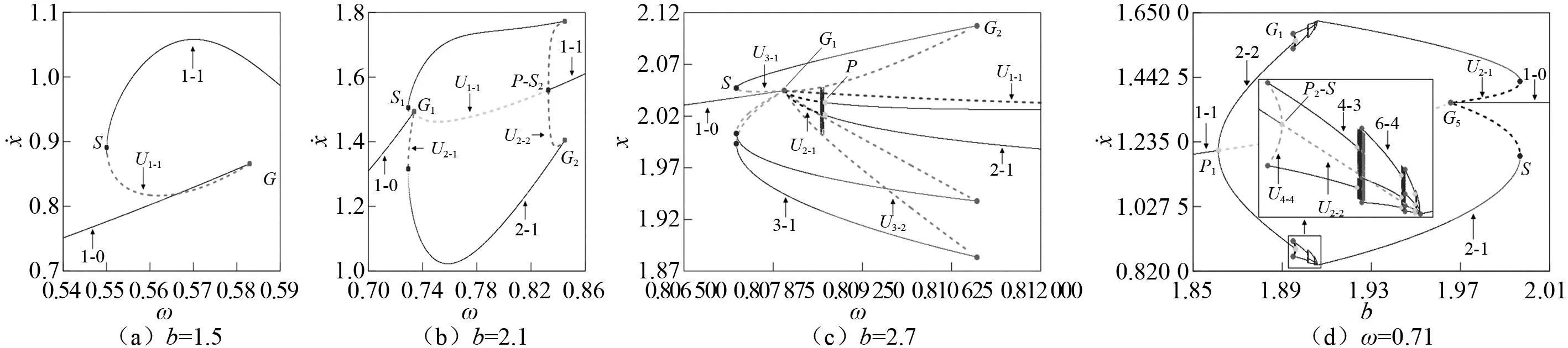
图3 1-0与1-1运动的转迁
图3(a)取b=1.5,描述了1-0与1-1吸引子转迁过程中的不连续擦边分岔和鞍结分岔。U1-1吸引子分支连接两个稳定吸引子分支,形成迟滞区。
在SIR0-S内,2-1吸引子的参数域面积最大,因此,图3(b)用来描述1-0与 1-1吸引子经2-1吸引子转迁的路径。减小ω当ω=0.832 828 37 (P)时,Floquet乘子λ1=-1.000 000和λ2=-0.289 059,系统发生周期倍化分岔导致1-1吸引子跳跃为2-1吸引子,周期倍化分岔表现出亚临界特征。为了详细揭示亚临界周期倍化分岔响应,减小分岔参数ω变化的步长(取Δω=1×10-8),由P点开始数值延拓周期2吸引子的存在性与稳定性。发现在P点,系统产生稳定的2-2吸引子。但是,该2-2吸引子持续的ω长度仅为2×10-7。当ω=0.832 828 35时,Floquet乘子λ1=0.999 996和λ2=0.089 894,2-2吸引子经鞍结分岔失去稳定性,产生向后弯曲的U2-2吸引子分支。此后,增大ω,U2-2吸引子分支与2-1吸引子分支在G2点相遇。可见,在P点的微小邻域内,鞍结分岔S2使系统终态发生跳跃,周期倍化分岔才表现出亚临界特征,我们把这一分岔过程称为鞍结型周期倍化分岔(P-S2)。在G1点,1-0吸引子的不连续擦边分岔产生向前持续的U1-1吸引子分支,同时产生向后弯曲的U2-1吸引子分支。图3(a)和图3(b)中U1-1吸引子的Floquet 乘子分别如图4(a)和图4(b)所示。
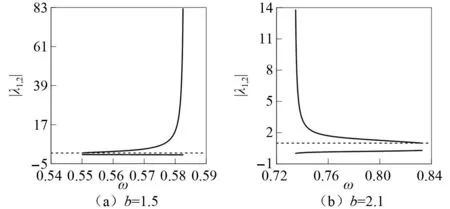
图4 U1-1吸引子的 Floquet 乘子
b=2.7时,1-0与1-1吸引子经SIR0-S的转迁如图3(c)所示。图3(c)中省略的2-1、U1-1吸引子与1-1吸引子之间的分岔与图3(b)相同。图3(c)描述的动力学主要表现在:①在G1点,1-0吸引子的不连续擦边分岔产生四个不稳定吸引子分支,分别是向前持续的U1-1、U2-1和U3-2以及向后弯曲的U3-1。U1-1和U2-1吸引子经周期倍化分岔获得稳定(参见图3(b)和(c)),而U3-1和U3-2吸引子分支分别连接3-1吸引子的边界点S和G2。由于1-0吸引子的擦边分岔可产生Uk-1(k=1, 2, 3,…)吸引子序列,因此,SIR0-S内周期吸引子的主要模式为k-1(k=2, 3,…);②减小b, 2-1吸引子经亚临界周期倍化分岔产生混沌,然后与U3-2吸引子碰撞经边界激变消失;③不连续擦边分岔和鞍结型周期倍化分岔引起的多吸引子共存使1-0与1-1吸引子之间的转迁更加复杂。
图3(d)取ω=0.71,描述了1-0与1-1吸引子转迁过程中的周期吸引子模式多样性以及鞍结型和亚临界周期倍化分岔、擦边分岔和边界激变等不连续分岔行为。4-3、6-4、8-5等2k-(k+1) (k=2, 3, 4, …)模式序列的出现使SIR0-S内的吸引子模式多样性和规律性特征更加明显。1-1吸引子的周期倍化分岔P1是超临界的,2-2吸引子的周期倍化分岔P2为鞍结型(P2-S),2k-(k+1)吸引子的周期倍化分岔是亚临界的。P2-S产生的U4-4吸引子最终与4-3吸引子相遇,导致系统发生擦边分岔G1。图5为6-4和混沌吸引子共存时的吸引域,分别用白色和灰色表示。由于混沌吸引子包含两部分且都很小,图5(a)和图5(b)的右侧图为左侧图中一部分混沌吸引子的放大。增大ω,6-4吸引子的吸引域逐渐增大,吸引域边界及位于边界上的U6-5吸引子向混沌吸引子逐渐靠近,直至碰撞,系统发生边界激变导致混沌吸引子突然消失。而当ω减小时,6-4吸引子终止于擦边分岔。

图5 吸引域
由图3可知,周期吸引子的鞍结型周期倍化分岔使系统响应表现出亚临界特征。为了进一步揭示周期倍化分岔邻域内的动力学随系统参数的演化,并确定SIR0-S下边界线的分岔类型,分别取ω=0.75、078、0.79和0.81,数值延拓1-1与2-1吸引子之间的转迁,结果如图6所示。ω=0.75时,1-1吸引子的周期倍化分岔P是超临界的。2-1与2-2吸引子经不连续擦边分岔G和鞍结分岔S互相转迁。分岔点G和S之间的距离即U2-2吸引子持续的ω长度为0.000 964 78。增大ω,G点逐渐远离S点,但P点向S点迅速靠近,2-2吸引子的区间明显变窄。当ω=0.81时,分岔点G和S之间的距离扩大至0.098 497 91,但是分岔点P和S之间的距离缩短为1×10-8。因此,S演变为P诱导的鞍结分岔,使P表现出亚临界特征。

图6 周期倍化分岔的演化
结合图2(b)、图3和图6可知,标准型亚谐包含域SIRm-S的上边界为1-m吸引子的不连续擦边分岔线,而下边界为1-(m+1)吸引子的超临界和鞍结型周期倍化分岔线。相邻不连续擦边分岔线的节点为退化擦边分岔点。由图2(c)可知,节点‘+’为1-0吸引子的退化擦边分岔点和1-1吸引子的余维二分岔点,连接1-0与1-1吸引子之间以及1-0与2-1吸引子之间由不连续擦边分岔线和鞍结分岔线形成的两个窄迟滞域,以及1-1吸引子的超临界周期倍化分岔线。
3.2 非标准型亚谐包含域内的动力学
图2(d)描述了非标准型亚谐包含域SIR2-N的两参数动力学。与标准型亚谐包含域相比较,由于混沌区域和周期吸引子模式增多,SIR2-N内的动力学更加复杂。在SIRm-S内,系统的主要响应为k-(km+1)吸引子,但是在SIR2-N内,系统的主要响应为2-5、2-6和混沌吸引子。
取ω=0.412,1-2与1-3吸引子经SIR2-N的转迁如图7(a)所示。1-2吸引子的周期倍化分岔P1是超临界的。1-3和2-5吸引子的周期倍化分岔为鞍结型(P-S),由此产生的U2-6和U4-10吸引子分别终止于擦边分岔点G1和G2。此外,不稳定吸引子的擦边分岔G4将U1-2和U1-3吸引子联系起来。如图7(b)所示,增大ω当ω=0.43时,1-3吸引子的周期倍化分岔由鞍结型变为超临界,1-2吸引子的分岔由周期倍化分岔变为不连续擦边分岔产生向前持续的U1-3和向后弯曲的U2-5。U2-5吸引子在S1点获得稳定,同时恢复b减小的变化方向。2-5吸引子在G2点经不连续擦边分岔产生向后弯曲的U4-11,然后在S2点获得稳定。图7(c)描述了1-2吸引子经不连续擦边分岔演化为3-7吸引子的过程。由前面的分析可知,1-m吸引子的不连续擦边分岔可产生Uk-(km+1)吸引子序列,从而在1-m与1-(m+1)吸引子的转迁过程中出现主要响应为k-(km+1)吸引子序列的亚谐包含域。

图7 1-2与1-3吸引子的转迁
取b=0.65,1-2吸引子及SIR2-N内k-(2k+1)吸引子的分岔如图7(d)所示。1-2吸引子的擦边分岔G1使系统终态直接表现为混沌吸引子。特别强调的是,系统在G1点之前发生了擦边诱导的鞍结分岔,并形成迟滞区。因此,迟滞区内的不稳定吸引子为U1-2,而不是U1-3,该分支连接两个不同的1-2吸引子分支。2-5、3-7等k-(2k+1)吸引子的周期倍化分岔是超临界的。k-(2k+1) (k≥3) 吸引子与混沌吸引子在一定参数区间共存。增大ω,混沌吸引子经边界激变消失,而当ω减小时,k-(2k+1)吸引子终止于擦边分岔。
取b=0.56,系统响应经SIR2-N的分岔如图7(e)所示。G1~G3均为不连续擦边分岔,分别产生的U1-3、U2-6和U4-11吸引子经鞍结分岔获得稳定。P1~P4均为超临界周期倍化分岔。减小ω,在G1点,系统终态由1-3直接跳跃为2-6,随后经周期倍化序列通向混沌。增大ω,2-5吸引子的周期倍化序列被不连续擦边分岔G3中断,系统终态最终经4-11吸引子的周期倍化序列通向混沌。
4 预压量对系统动力学的影响
数值结果表明,预压量d对系统的两参数动力学,尤其是迟滞域和亚谐包含域的形成机理有着较大的影响。取d=0.05、0.02和0,其余参数与参数(1)相同,数值仿真系统在ω-b参数平面的动力学响应分别如图8(a)、图8(b)和图8(c)所示。图8(d)为图8(c)的局部放大。对比图2和图8可知,减小d,亚谐包含域的数量和面积以及周期1吸引子模式明显减少。当d=0时,非标准型亚谐包含域消失。SIRm出现在紧邻两参数边界线的1-(m+1)吸引子的参数域内,使得亚谐包含域的形成机理发生改变。亚谐包含域内的周期吸引子模式减少,混沌吸引子消失,动力学变得相对简单。图9为1-2与1-3吸引子之间转迁的单参数分岔图。

图8 两参数动力学

图9 1-2与1-3吸引子的转迁
图9(a)表明,当d=0时,相邻1-m与1-(m+1)吸引子可以经连续擦边分岔互相转迁。图9(b)揭示了迟滞域的形成机理。在擦边分岔G附近,鞍结分岔S1使1-3吸引子失去稳定性,从而使系统终态跳跃为另一个1-3吸引子。U1-3吸引子连接两个鞍结分岔点S1和S2。分岔点G和S1之间的距离为0.000 115 88,因此,S1为G诱导的分岔,使G表现出不连续特征,从而引起迟滞现象。
如图8(d)所示,系统在SIR2内的主要响应为2-5和2-6吸引子。取0.43,1-2与1-3吸引子经SIR2的转迁如图9(c)所示。减小ω,周期1吸引子的分岔过程为:1-2→G1→1-3→P1→U1-3→P2→1-3。产生于擦边分岔G1点的1-3吸引子持续的ω长度仅为0.000 162 01,随后在周期倍化分岔P1点失去稳定性。因此,P1为G1诱导的分岔,使系统响应进入SIR2。U1-3吸引子在P2点恢复稳定,系统响应退出SIR2表现为1-3吸引子。2-5与2-6吸引子之间经连续擦边分岔互相转迁。
当参数d由0.1减小为0时,迟滞域和亚谐包含域的形成机理发生本质的变化。ω-b参数平面内,当d=0.1时,1-m吸引子的不连续擦边分岔可产生Uk-(km+1)吸引子,从而在相邻1-m吸引子的转迁过程中形成特殊转迁域。当k只等于1时形成迟滞域,否则形成亚谐包含域。1-m吸引子的擦边分岔仅在相邻特殊转迁域的连接点是连续的。当d=0时,1-m吸引子的擦边分岔是连续的,但是擦边诱导的鞍结分岔或周期倍化分岔使1-(m+1)吸引子失去稳定性,从而在相邻1-m吸引子的转迁过程中形成迟滞域或亚谐包含域。U1-(m+1)吸引子存在于整个迟滞域和亚谐包含域内。然后,同类型的分岔使U1-(m+1)吸引子获得稳定,1-m吸引子经迟滞域或亚谐包含域转迁为1-(m+1)吸引子。
取b=0.564,图9(d)用来描述SIR2内的稳定周期吸引子模式和分岔。ω减小时的分岔过程为:1-2→G→1-3→P→2-6→SubP→4-11→P→8-22→P→4-11→G→4-10→P→2-5。2-6吸引子的周期倍化分岔是亚临界的,其余周期倍化分岔都是超临界的。当ω=0.445 393 38时,2-6吸引子失去稳定性,同时产生向后弯曲的U4-12吸引子。随后,系统发生不稳定吸引子的擦边分岔产生U4-11吸引子,与4-11吸引子在鞍结分岔点相遇。
减小ξ可使亚谐包含域的面积增大、亚谐周期吸引子模式增多。因此,为了深化揭示d=0时亚谐包含域内的动力学,ξ由0.08减小至0.06时的动力学响应如图10(a)所示。对比图8(c)和图10(a)可知,减小ξ,周期1吸引子的模式增多,亚谐包含域的数量和面积明显增大,且SIRm(m≥2)出现非标准型。但是,需要指出的是,ξ的变化没有改变擦边分岔特征以及SIRm-S的形成机理。由图2和图10(a)可见,在两组参数条件下,系统在SIR2-N内具有相似的动力学行为,但是SIRm-S内的动力学明显不同,主要体现在两个方面:(1) SIRm-S内的亚谐周期吸引子模式改变。图10(a)所示SIRm-S内没有k-(km+1)吸引子序列; (2) SIRm-S的形成机理以及SIRm-S内周期吸引子的分岔发生改变。
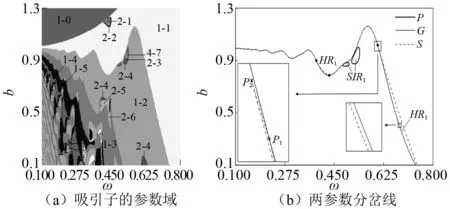
图10 两参数动力学, d=0, ξ=0.06
图10(b)为1-1与1-2吸引子的两参数分岔线,进一步验证了d=0时迟滞域和亚谐包含域的形成机理。图10中,擦边和周期倍化分岔线分别用细实线和粗实线表示,鞍结分岔线用虚线表示。周期倍化和鞍结分岔线都是闭合曲线,分别形成亚谐包含域和迟滞域。部分周期倍化和鞍结分岔线紧贴擦边分岔线,构成擦边诱导的分岔线。在该部分分岔线上,由擦边分岔产生的1-2吸引子失稳,系统响应嵌入特殊转迁域。
5 结 论
本文考虑工程实际中存在的含预紧弹簧机械碰撞系统的简化力学模型,构建由光滑流映射和不连续映射复合的Poincaré映射,给出Floquet乘子计算的数值方法。数值仿真了系统在两参数平面的周期吸引子模式及其参数域,结合Runge-Kutta法、打靶法、延续法和胞映射法研究了周期1吸引子的稳定性与演化规律以及不连续擦边分岔、擦边诱导的分岔、鞍结型和亚临界周期倍化分岔、激变等不连续分岔行为,揭示了迟滞域和亚谐包含域的形成机理。
当d不等于0时,1-m吸引子的不连续擦边分岔可产生Uk-(km+1)吸引子序列,从而在相邻1-m与1-(m+1)吸引子的转迁过程中产生迟滞域和亚谐包含域,亚谐包含域内周期吸引子的主要模式为k-(km+1)。
当d=0时,1-m吸引子的擦边分岔是连续的,但是擦边诱导的鞍结分岔或周期倍化分岔在相邻1-m吸引子的转迁过程中形成迟滞域或亚谐包含域。亚谐包含域SIRm内亚谐周期吸引子的主要模式为2-(2m+1)和2-2(m+1)。
在周期倍化分岔的微小邻域内,鞍结分岔使系统终态发生跳跃,周期倍化分岔表现出亚临界特征,我们把这一分岔过程称为鞍结型周期倍化分岔。不连续擦边分岔、亚临界周期倍化分岔和鞍结型周期倍化分岔在相邻吸引子的转迁中引起多吸引子共存。当周期吸引子与混沌共存时,混沌吸引子经边界激变消失。
本文以新的视角发现了许多复杂的新现象,如擦边和周期倍化诱导的分岔、不稳定吸引子的擦边分岔等。鞍结型周期倍化分岔的发现和定义将进一步丰富非光滑系统的动力学。研究结果能够为工程实际含预紧弹簧机械碰撞系统的参数设计与选择提供参考。通过两参数动力学以及共存吸引子的全局动力学分析可以实现系统的动态优化设计,使系统在更大的参数空间呈现期望的吸引子模式。
——如何培养学生的创新思维

