一类对称约束碰振系统的余维二擦边分岔的存在条件

徐洁琼， 陈慧莹， 伍 帅， 袁 泉

(广西大学 数学与信息科学学院， 南宁 530004)

碰撞振动系统作为一类典型的非光滑系统，除了具有光滑分岔(余维一Hopf分岔和Neimark-Sacker分岔，余维二Hopf-flip分岔、Hopf-Hopf分岔、退化Hopf分岔等[1-2])外，还具有非光滑系统所特有的非光滑分岔现象，(如擦边分岔。余维一非光滑分岔(擦边分岔、滑动分岔以及角点分岔)的理论研究已经比较完善。基于最早由Nordmark[3-4]提出的局部不连续映射方法，建立了在不同非光滑系统中非光滑分岔的规范型[5-6]。关于余维二非光滑分岔的研究目前还没有统一的结论，主要是针对不同的问题分析特定的余维二非光滑分岔现象。Kowalczyk等[7]针对非光滑微分系统的极限环的余维二非光滑分岔提出了一种分类策略。类似光滑系统的余维二分岔的分类方法，余维二擦边分岔被划分为三种类型，分别是：第一种擦边点退化，即，决定擦边点局部向量场性质的解析条件发生退化；第二种退化环擦边(非双曲)，也可以看成是在同一组参数下光滑分岔和非光滑分岔同时发生；以及第三种两个擦边事件同时发生。Yin等[8]对单自由度碰撞振子的退化擦边分岔行为进行分析，利用不连续映射的方法研究碰撞系统擦边动力学行为，并找出单自由度碰撞振子退化分岔条件，推导出碰撞周期运动退化擦边分岔的存在条件。Thota等[9]对单自由度碰撞振子的余维二擦边分岔进行了研究，并通过不连续映射的方法得到擦边分岔的开折图，分析了余维一分岔对余维二分岔点的动力学影响。Zhao等[10]对微机械系统中的余维二和余维三分岔进行研究，提出一种分析方法来预测两个余维二分岔点的邻域的分岔行为。Jiang等[11-12]将刚性碰撞振动系统的不连续性几何概念拓展到弹性碰撞振动系统中，研究了具有单侧弹性约束的碰撞振动系统的擦边分岔机理。并研究了单侧弹性和刚性约束冲击振子中擦边分岔的区别，并对这两种振子的擦边分岔进行分类。Yin等[13]推导了退化擦边碰撞系统的高阶零时间不连续映射，并通过对近擦边碰撞周期运动的存在性分析，对低阶和高阶截断的比较，说明了利用高阶零时间不连续映射分析退化擦边分岔的必要性和可行性。Xu等[14]基于显式临界准则和不连续映射方法，研究了三自由度振动冲击系统周期解的稳定性和分岔问题，解释了在擦边周期运动附近，吸引子不连续跳跃和吸引子共存的原因。

除了单侧约束碰振系统，在许多实际工程问题中也会涉及到具有双侧约束碰撞振动系统，例如齿轮传动系统、连接设备、高速铁路列车轮轨互相作用、核反应堆中的热交换器管道等。 吕小红等[15]对具有双侧约束碰撞振动系统进行研究，得到倍周期分岔和擦边分岔通向混沌的路径，对混沌行为实施了控制。井红岩[16]选取以双侧约束的自带冠叶片作为研究对象，建立了发生双侧碰撞的自带冠叶片振动系统模型,推导了碰撞振动系统的周期解，并对周期运动特性进行了有效分析。Xu等[17]研究了具有对称约束的n自由度碰撞系统的擦边分岔稳定性条件的退化，得出该类系统余维二擦边分岔的显式公式。本文对具有对称约束的二自由度碰撞系统的第二类余维二分岔进行分析，推导了一类余维二擦边分岔的存在条件。文章结构如下：第一章，双擦周期运动的存在条件；第二章，基于不连续映射的复合Poincaré映射；第三章，近擦边动力学分析；第四章，余维二擦边分岔的存在条件；第五章，结论。

1 双擦周期运动的存在条件

1.1 力学模型

本文考虑一个具有对称约束的二自由度刚性碰撞振动系统，如图1所示。该系统由质量为M1和M2的振子组成、振子分别由刚度为K1和K2的线性弹簧以及阻尼系数为C1和C2的线性阻尼器相连接。在简谐激振力Pi(ΩT+τ),(i=1,2)的作用下质块沿水平方向往返运动。振子的位移分别用X1和X2表示，系统具有对称性的约束面A和C，质量M1的质块在约束面A和C之间移动。质量M1的质块位移X1为B或-B时，将与约束面A或C发生碰撞。碰撞恢复系数为R，假设与力的周期相比，刚性碰撞振动系统碰撞持续时间可以忽略不计。

图1 系统模型

其中“″”和“′”分别是对时间t的二阶导数和一阶导数。

假定上述力学模型中的阻尼为Rayleigh型的比例阻尼，令p0=|p1|+|p2|，作如下变换

无碰撞时，系统经过无量纲变化之后的运动方程为

(1)

质块M1的碰撞冲击方程为

设Ψ为碰撞振动系统(1)的正则模态矩阵，ω1和ω2表示质块和约束面无接触情况下系统的固有频率。作坐标变换x=Ψγ，得到系统的运动方程如下

(2)

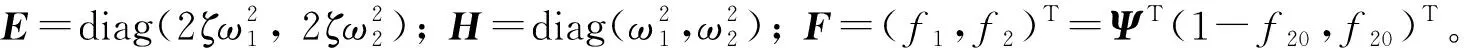
1.2 双擦周期运动的存在条件

利用模态叠加法求解碰撞振动系统(2)可得

bj1sinωdj(t-t0)))+Ajsin(ωt+τ)+

Bjcos(ωt+τ),t0≤t≤t1,(i=1,2)

(3)

bj2sinωdj(t-t1)))+Ajsin(ωt+τ)+

Bjcos(ωt+τ),t1≤t≤t2,(i=1,2)

(4)

(5)

且在约束面A和C擦边点处振子M1的加速度分别小于零和大于零。

2 基于不连续映射的复合Poincaré映射

令θ=ωtmod(2π)表示激励的相位，引入状态变量X=(x1v1x2v2d)T∈R5，则有

(6)

式中：v1和v2分别代表质块M1和M2的速度；a1和a2代表质块M1和M2的加速度。

当振子M1的位移x1满足|x1|=d时，振子M1与约束面A或C发生接触(擦边或者碰撞)，定义不连续面D1，D2，D1=X|hD1(X)=d-x1=0,D2=X|hD2(X)=-d-x1=0。

gi(X)=(x1, -Rv1,x2,v2,d)T

其中i=1,2。

设X*1，X*2为不连续面D1，D2处的擦边点，则：hD1(X*1)=0,hD2(X*2)=0。

为了分析擦边点附近的动力学行为，引进零时间不连续映射。根据不连续映射方法，得到DM1和DM2的不连续映射如下

DM1=

DM2=

(7)

其中β1，β2满足：

β1=

β2=

选择两个固定相位角θ*1，θ*2为截面，其截面满足以下形式

利用光滑流可以定义映P1s:P1→P2和P2s:P2→P1，使得P1s(X*1)=X*2和P2s(X*2)=X*1。选择P1为Poincaré截面，复合光滑映射和不连续映射，得到分析近擦边动力学的复合Poincaré映射：

P=P2s∘DM2∘P1s∘DM1

在X*1邻域展开光滑映射P1s(X)及函数hD1(X)，并舍去高阶项得到：

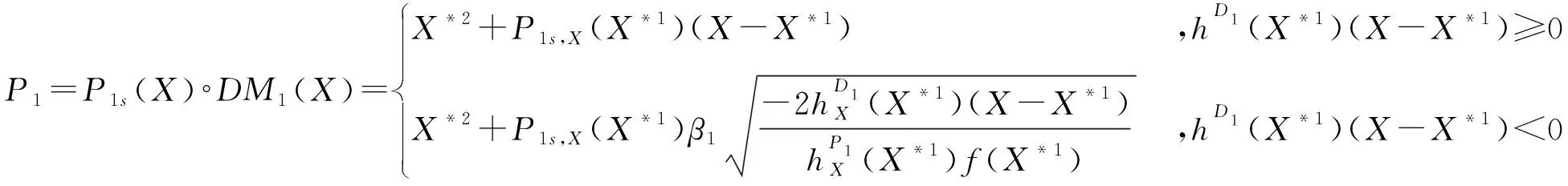
(8)

3 近擦边动力学分析

3.1 存在性条件

考虑碰振系统发生1/1/n周期运动，即：在n个外激励周期，振子在一个周期与不连续面D1、D2先后发生碰撞，在之后的n-1个周期无碰撞现象发生，第n+1个周期时再次与D1、D2发生碰撞的运动现象。

当发生1/1/n碰撞周期运动时，利用复合映射(8)求不动点。

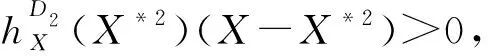
为进行简化计算令

P1s,X[P2s,X∘DM2∘P1s,X∘DM1](X)=X*2+P1s,XP2s,XQ

P2s,XP1s,X[P2s,X∘DM2∘P1s,X∘DM1](X)=

X*1+P2s,XP1s,XP2s,XQ

依此类推

P1s,X(P2s,XP1s,X)n-2[P2s,X∘DM2∘P1s,X∘DM1](X)=X*2+P1s,X(P2s,XP1s,X)n-2P2s,XQ(n≥2)

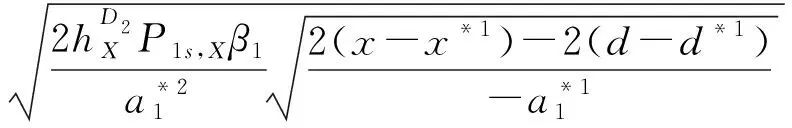
(9)

3.2 分岔条件

分析1/1/n周期运动的分岔条件，先求出复合映射的Jacobian矩阵，利用其特征值找出相应的鞍结分岔线和倍周期分岔线，具体过程如下。

C=(1 0 0 0 0)，

则可以得到如下等式

x-x*1=C(X-X*1)=C(P2s,XP1s,X)n-1·

(10)

(11)

C(P2s,XP1s,X)(n-1)P2s,Xβ2=(1 0 0 0 0)·

(12)

为方便进一步对Y进行求解，先对Y进行平方操作得到等式(13)，并将式(10)～(12)代入式(13)中，得出Y与d-d*1相关的式(14)。

(13)

(14)

利用对n次复合映射Jacobian矩阵的特征值进行求解，进一步找出对应的鞍结分岔和倍周期分岔发生时所满足的条件，有基本分岔理论可知，特征值λ=1时对应鞍结分岔，特征值λ=-1对应倍周期分岔。n次复合映射Jacobian矩阵DPs如下

其中Q满足

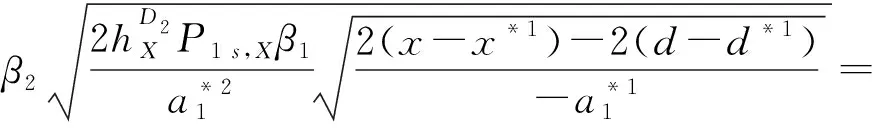
由此容易计算出n次复合映射PS的Jacobian矩阵如下

(15)

化简计算可得

(16)

将λ=1代入式(16)，并联立关于Y的式(14)，得到周期运动发生鞍结分岔的条件

将λ=-1代入式(16)，并联立关于Y的式(14)，得到发生倍周期分岔的条件

令

并使用SN 和PD分别代表鞍结点分岔线和倍周期分岔，分岔条件可以写成如下形式

(17)

4 余维二擦边分岔的存在条件

根据上一节推导出的两类分岔的表达式(17)，得出发生余维二擦边分岔条件的解析表达式，即，以下条件成立时发生余维二擦边分岔

(18)

容易发现，当ζn取值为0，碰撞振动系统发生余维二擦边分岔。对于周期n为1的碰撞周期运动，选定以下参数um=10.0，uk=5.0，uc=5.0，R=0.8，f20=0.0，ζ=0.05，进行数值模拟。根据式(5)和上述余维二擦边分岔条件(式(18))，同时作出鞍结分岔线、倍周期分岔线以及擦边曲线，找出三条曲线的交点，即余维二擦边分岔点，如图2所示。从图中我们可以看到三条不同的曲线，用长虚线表示的曲线对应鞍结分岔曲线，实线对应擦边曲线，用短虚线表示的曲线对应倍周期分岔曲线(图3为图2的局部放大图像)。在图2中可以看出三类曲线在ω∈[0.1,3]范围内具有多个交点，即在 (0.109，1.223)、(0.161，1.251)、(0.218，1.296)、(0.335 5，1.453 2)、(0.611，4.906)和(1.233，2.247)等点处满足余维二擦边分岔条件(18)，发生了余维二擦边分岔。以频率ω作为变化参数，根据擦边分岔条件，即达式(5)，画出随着频率ω变化d的曲线，即擦边分岔曲线。然后找到曲线上满足ξn=0的点，用*号表示，得到碰撞振动系统余维二擦边分岔点的分布情况，如图4所示。图4展现了周期n取值为时，碰撞振动系统余维二擦边分岔点的分布情况，容易看出余维二分岔点主要集中在曲线的左端，即较小的ω值处。

图2 1/1/1碰撞周期运动退化点附近动力学行为

图3 局部放大图像

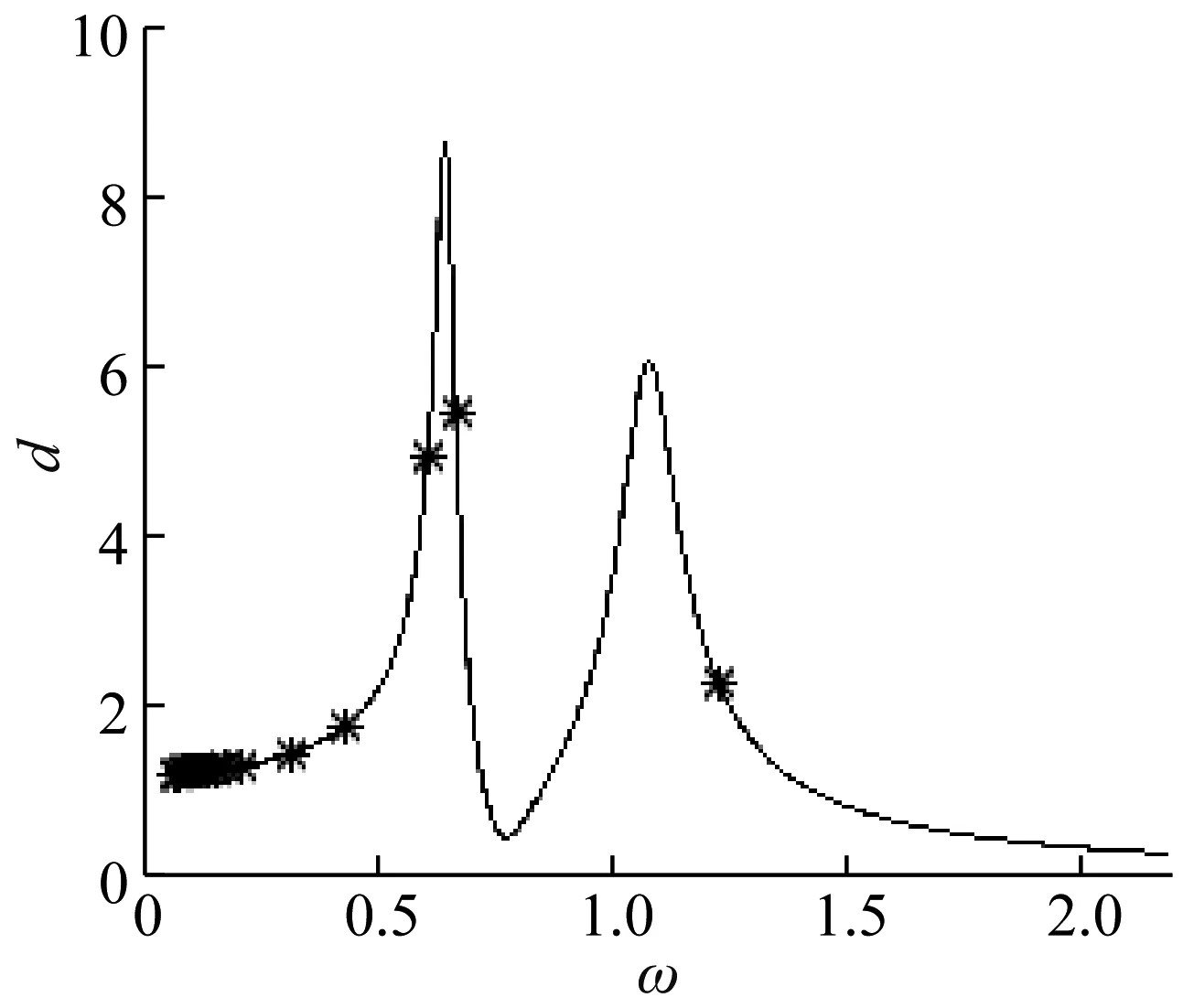
图4 周期n=1运动的退化点

5 结 论

本文针对一个具体的二自由度对称约束的碰撞振动系统，详细讨论了第二种余维二擦边分岔，即，在同一组参数下光滑分岔和非光滑分岔同时发生的存在条件。经过详细推导得到了该类余维二擦边分岔存在条件的解析表达式。余维二擦边分岔被分为三类，但是，在每一类中发生余维二分岔的情况繁多，将进一步对更多的分岔情况进行分析和总结。