基于实时可达域的高速飞行器分组队形优化

李宇航，张 兵，姜 利，王 智，白文露

(1.北京宇航系统工程研究所，北京 100076；2.中国运载火箭技术研究院，北京 100076)

0 引言

随着人工智能技术的快速发展，各国开始对集群协同技术提出智能化的要求[1]，队形优化作为协同智能决策的关键技术备受关注。队形优化是指在飞行器集群完成相关飞行任务的过程中，为其设计合理的编队队形，从而提高集群的安全性、灵活性以及任务执行效率。目前有关队形优化的研究通常是针对某一特定场景设计最优队形[2-5]或针对某一基本队形的队形参数进行优化[6-7]，而没有做到“形状级”的队形设计，同时，研究对象多集中于低速飞行器[8]。

本文在现有研究的基础上，考虑高速飞行器实际控制特点，对飞行器集群的编队队形形状和参数同时进行优化，允许飞行器集群中各成员具有不同的飞行任务，研究分组条件下的飞行器队形优化方法。首先，在建立高速飞行器运动模型的基础上，利用数值计算方法构建不同初始状态下飞行器实时可达域数据库；其次，设计并训练神经网络以实现对实时可达域的快速精确预测；再次，建立适用于高速飞行器集群的编队飞行效能指标体系及适应度函数，建立队形优化模型并利用改进遗传算法求解；最后，对神经网络快速预测实时可达域、不同任务下分组队形优化、集群成员数量变化下的动态队形优化进行仿真分析。

1 高速飞行器实时可达域快速计算

实时可达域是指飞行器在沿预定轨迹飞行过程中，基于当前飞行状态和相关约束，在一定时间后能够到达的空间区域[9]，如图1所示，其与飞行器的初始状态、运动模型和控制能力紧密相关。图中V为飞行器速度大小，θ为飞行器弹道倾角，ψ为飞行器航迹偏角。

图1 飞行器实时可达域示意图Fig.1 Schematic diagram of real-time reachable domain of aircraft

高速飞行器设计编队队形时需要考虑队形的可实现性，因此要对其可能到达的飞行边界进行建模分析和快速计算以确定实时可达域，为编队队形优化提供约束条件。

1.1 飞行器运动模型

建立合理的运动模型是计算实时可达域的基础，高速飞行器是一个复杂动力学系统，为简化模型、提高计算速度，同时不失一般性作如下简化：

1)将飞行器视为理想质点，作用在飞行器上的力矩在每一瞬时都处于平衡状态；

2)符合标准大气模型；

3)忽略地球扁率，假设地球自转角速度恒定；

4)飞行器控制方式采用BTT转弯模式。

定义发射坐标系坐标原点为发射点，x轴指向目的地，y轴在纵向平面内垂直于x轴，z轴与xoy平面垂直并构成右手坐标系。发射坐标系依次绕z轴、y轴旋转θ，ψ可得到弹道坐标系oxHyHzH，如图2所示，图中单位无量纲处理，全文同。在发射坐标系下建立高速飞行器运动方程，见式(1)。

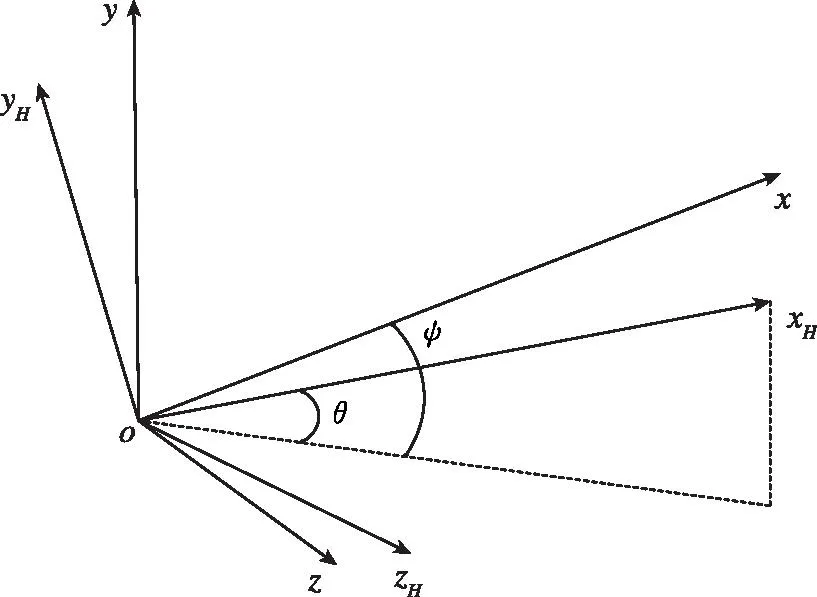
图2 坐标系转换示意图Fig.2 Coordinate system conversion diagram

(1)

1.2 实时可达域快速计算

利用数值积分法求解实时可达域速度慢，难以直接在线进行。为了快速获得飞行器实时可达域数据，通过大量离线仿真，获得飞行器在不同初始状态下的实时可达域计算结果，并建立数据库，采用基于BP神经网络的方法，利用数据库训练神经网络，实现对飞行器实时可达域的快速预测。

1.2.1 实时可达域模型描述

考虑到高速飞行器在航向上控制难度大，队形设计一般在横向和高度向进行，因此实时可达域也在这两个方向计算。实时可达域计算在飞行器发射平移坐标系olxlylzl中进行，其坐标原点位于飞行器质心，各轴方向平行于发射坐标系oxyz。

对于任意给定的飞行器初始状态，按照一定间隔在[0，π]范围内选取若干倾侧角，分别在攻角为最大可用攻角和最小可用攻角的设定下，采用四阶龙格库塔法对飞行器轨迹进行积分，即可得到该状态下飞行器的实时可达域信息，如图3所示。为便于描述，对实时可达域进行简化，将其看作是由相同圆心位置的上下两个半径不同的半圆拼接而成的，同时要求简化模型能被真实实时可达域完全覆盖，其可由圆心位置[zl0，yl0]和半径[R，r]进行描述。

图3 高速飞行器实时可达域及其简化模型Fig.3 Real-time reachable domain and simplified model of high speed aircraft

1.2.2 训练数据库建立

通过对不同初始状态的飞行器进行仿真计算，发现当飞行器的运动模型确定后，其实时可达域主要受初始高度、速度、弹道倾角、航迹偏角以及飞行时间等参数的影响[10]。各参数对实时可达域的影响如图4所示。本文对上述5类参数进行组合，如图5所示。一共针对7×4×10×7×7=13 720组数据进行仿真计算，并根据计算结果构建实时可达域数据库。

(a)不同初始高度下实时可达域

图5 高速飞行器实时可达域数据库的参数组合情况Fig.5 High-speed aircraft real-time reachable domain database parameters combination

1.2.3 神经网络快速预测

图6 神经网络结构示意图Fig.6 Neural network structure

2 编队飞行队形优化

通常，根据所执行任务的不同，高速飞行器集群以不同队形进行编队飞行从而提高飞行效率。该过程涉及编队队形优化技术，其是指依据飞行任务、态势和复杂约束为飞行器集群生成期望的编队队形和相应的队形参数。本节将在设定编队队形参数的基础上，建立高速飞行器编队飞行效能指标体系与适应度函数，并依据改进遗传算法进行求解，得到最优编队飞行队形。

2.1 编队队形参数

高速飞行器由于飞行速度高，对通信和规划决策的实时性要求苛刻，通常采用主-从式控制方案[12]，采用主-从式相对运动模型来描述编队队形。本文在主飞行器的发射平移坐标系下，以从飞行器相对于主飞行器的位置作为待优化的队形参数，如图7所示。

图7 主-从式编队队形及队形参数Fig.7 Master-slave formation and formation parameters

设第i个从飞行器相对主飞行器的位置为rli=[yli，zli]，则整个编队队形可由矢量[yl1，zl1，yl2，zl2，…，yl，n-1，zl，n-1]表示，其中n为飞行器集群成员数量。由此当主飞行器在发射坐标系下的空间位置确定后，整个编队所有成员的期望位置也将唯一确定。

2.2 队形优化模型

2.2.1 编队飞行效能指标体系

高速飞行器编队飞行效能指标体系包括通过项指标、通用项指标和专用项指标，如图8所示。其中通过项指标包括飞行边界和飞行能力，主要衡量所设计编队队形能否实现，是保证飞行器集群的基本要求；通用项指标包括机动互不干扰、通信覆盖范围和能量消耗指标，对任何飞行任务都希望其尽可能最优；专用项指标包括编队避障、探测范围和探测精度等指标，飞行器集群可根据不同飞行任务选择与之相适应的专用项指标，以提高飞行效能。

图8 编队飞行效能指标体系Fig.8 Formation flight efficiency system

2.2.2 适应度函数

依据编队飞行效能指标体系建立适用于高速飞行器队形优化的适应度函数，见式(2)。

(2)

式中，f为加权处理后的适应度函数；f1，f2分别为飞行边界和飞行能力指标的适应度函数；ωi为指标体系中第i个指标的权重；fi为第i个指标的适应度函数；NI为指标个数。

(1)飞行边界

飞行边界是指各从飞行器允许偏离主飞行器位置的最大值，其由无线数据链传输性能以及飞行器机动能力综合确定，是保证各飞行器编队飞行的基本要求。本文以主飞行器为中心，建立矩形包络Ω1，如图9所示，所有从飞行器在该包络内即可满足飞行边界指标要求。

图9 飞行边界示意图Fig.9 Flight boundary diagram

考虑到飞行边界指标的重要性，将其设定为通过项指标。设计适应度函数

(3)

式中，Pj表示第j个飞行器的位置。

(2)飞行能力

飞行能力指标与飞行边界指标类似，是衡量编队队形能否实现的重要指标。不同于低速飞行器，高速飞行器可到达的空间区域受自身能力的限制较强，需利用飞行器实时可达域Ω2表征各飞行器的飞行能力，要求所设计编队队形应使各成员期望编队位置在其实时可达域内。将其设定为通过项指标。设计适应度函数

(4)

(3)机动互不干扰

机动互不干扰指标表征当飞行器集群机动飞行时，各成员间避免发生气动干扰甚至碰撞的能力。显然，在不考虑其他影响时，间距越大，飞行器集群的机动互不干扰能力越强，因此采用相邻编队成员间距离来衡量该项能力。将其设定为通用项指标。设计适应度函数

(5)

式中，f3j为第j个飞行器满足机动互不干扰指标的适应度函数，dis0为飞行器间安全间距，disj为第j个飞行器和第j+1个飞行器之间的距离。

(4)通信覆盖范围

(6)

式中，f4j为第j个飞行器满足通信覆盖范围指标的适应度函数；ξ0为最小离轴角；ξj为第j个飞行器相对主飞行器离轴角；k1为放大因子，通常取1.2～1.5。

能量消耗指标表征各飞行器飞向期望编队位置所消耗的能量多少。本文利用各飞行器期望编队位置与相同时间内其无控飞行到达的位置之差来衡量能量消耗。能量消耗指标是多飞行器集群编队飞行普遍适用的指标，设定其为通用项指标。设计适应度函数

(7)

式中，rzj，ryj分别表示第j个飞行器期望编队位置与无控飞行到达的位置之差在横向和高度向的分量；权重系数k2，k3根据控制能力确定，且满足k2+k3=1；rj为飞行器j实时可达域简化模型中下半圆的半径。

(6)编队避障

编队避障指标表征飞行器集群躲避障碍物减少损毁的能力。通常，根据障碍物距离、形式，为飞行器集群设定合适的期望间距，可有效减少飞行器集群的避障难度。设定其为专用项指标。设计适应度函数

(8)

式中，φ0为避障任务参考角，disMT为编队生成时刻主飞行器和障碍物之间的距离，disj，k为第j和第k行器之间的距离。

(7)探测范围

探测范围衡量飞行器集群能够探测到的空间区域大小，在各飞行器探测能力确定的情况下，希望集群更加分散。探测范围适用于执行探测任务的飞行器集群，设定其为专用项指标。设计适应度函数

术中发现有清亮的脑脊液溢出时，说明硬脊膜已经破损，应积极进行修补［17］。有多种硬脊膜损伤的修补方法，直接缝合法、筋膜或肌瓣包绕或补片式修复法、后侧筋膜严密缝合法［18］、生物蛋白胶-明胶海绵复合物修复法［19］。笔者认为不同的硬脊膜破损的分度应采取不同的治疗措施。

(9)

式中，ymin，ymax分别为集群成员在高度向的最小值和最大值；zmin，zmax分别为集群成员在横向的最小值和最大值；yΩ1，zΩ1分别为由飞行边界确定的高度向和横向范围。

(8)探测精度

探测精度衡量飞行器集群对目标的探测定位精度，在各飞行器探测能力确定的情况下，融合多个来自不同方向的探测数据可有效提高探测精度[13]。设定其为专用项指标。设计适应度函数

f8=1/(q11+q22+q33+q44)

(10)

式中，xjM，yjM，zjM分别为目标相对于第j个飞行器在航向、高度向和横向上的距离；q11，q22，q33，q44分别为矩阵Q的对角线元素。

2.3 队形优化算法

直接利用传统遗传算法求解队形优化问题收敛速度慢且易陷入局部最优，本文为其加入启发式信息和随机因子克服上述问题。在种群生成之初，依据相关指标启发式指导初始种群的生成。初始种群中任意一个个体的生成过程如下。

1)对于第一个飞行器，在其飞行边界Ω1和实时可达域Ω2内，以无控飞行所能到达的位置为期望位置，按照二维正态概率分布随机生成第一架飞行器的初始位置；

2)对于之后的飞行器，在其飞行边界Ω1和实时可达域Ω2内，同时考虑和前一飞行器机动互不干扰的距离要求，以无控飞行所能到达的位置为期望位置，按照二维正态概率分布随机生成初始位置；

3)将第一架飞行器和最后一架飞行器的横向位置之和作为扣除项，将所有飞行器横向位置与之作差，结果作为各成员新的初始位置；

4)对飞行器集群各成员位置进行编码形成个体片段，并将其串联起来作为种群中的一个个体individuali。

将预设数量的初始个体组合得到初始种群后，按照图10改进遗传算法流程进行迭代求解。

图10 改进遗传算法求解编队飞行队形优化流程图Fig.10 Improved genetic algorithm for formation flight formation optimization flow chart

3 仿真验证

3.1 实时可达域快速预测结果

针对图5所示参数组合建立的实时可达域数据库，随机选取训练样本数量13 500，测试样本220，设定学习率为0.002，离线训练次数为1 000次。对图6所示神经网络训练结果见表1、图11和图12。

表1 数值计算与神经网络方法时间对比Tab.1 Time comparison between numerical calculation and neural network method

图11 神经网络预测误差随训练次数变化曲线Fig.11 Neural network prediction error curves with training times

通过表1可以看出利用神经网络可大大提高实时可达域预测速度，从而保证队形的在线优化。从图11和图12可以看到神经网络对实时可达域简化模型4个描述参数的预测误差不大于0.5%。由于实时可达域简化模型被真实实时可达域完全覆盖，在应用神经网络预测结果时，可首先对其进行放缩，保证其在真实实时可达域内，提高队形优化模型输出结果的可靠性。

3.2 高速飞行器分组动态队形优化结果

3.2.1 不同任务下的分组队形优化

将高速飞行器集群分为若干执行不同任务的小组，分别为各组飞行器设置不同的任务，见表2。各项任务均需满足通过项指标及通用项指标，特别地，其中编队避障任务还需满足协同避撞指标，精确到达还需满足探测范围指标，精确探测还需满足探测精度指标。设置飞行时间为16 s，随机设置各飞行器初始状态，归一化优化结果见图13。

表2 飞行器集群各分组任务情况Tab.2 The task of each group of aircraft cluster

(a)实例1情况

3.2.2 分组动态队形优化

在飞行过程中，当部分飞行器发生故障或损耗时，需要动态调整队形。以实例1为例，考虑第3个分组中第1个和第2个飞行器发生故障时，其新队形见图14。可以看到当某个分组只剩1个飞行器后，会并入临近的分组，并配合临近分组执行其任务。

(a)第3个分组中1个飞行器故障

4 结束语

本文提出基于实时可达域的高速飞行器分组动态队形优化方法。仿真结果表明利用神经网络预测实时可达域大大提高了可达域计算速度，同时具有较高预测精度。利用改进遗传算法可对队形形状和参数同时进行优化，同时可以快速解决分组队形优化这一多目标多约束问题，使各个分组更好地执行其各自飞行任务。并入临近分组的原则可有效解决当部分飞行器发生故障或被击毁时的队形重构问题，研究成果具有重要的应用价值。