基于时间最优的机器人位姿同步轨迹规划方法*
曹钰婷,王金涛,刘明敏,樊志伟
(1.中国科学院沈阳自动化研究所机器人学国家重点实验室,沈阳 110016;2.中国科学院机器人与智能制造创新研究院,沈阳 110169;3.中国科学院大学,北京 100049;4.沈阳新松机器人自动化股份有限公司,沈阳 110168)
0 引言
目前,工业机器人被广泛应用于汽车、电子、轻工与航空航天等行业[1-2]。由于生产任务的加重和生产需求不断提高,制造业对工业机器人的性能提出了更高的要求:时间最优、能耗最优或冲击最优[3-4]。其中,时间最优代表效率更高,对于现代企业更有价值,所以优化机器人的运动时间在近年来一直备受广大学者关注。
工业机器人的时间最优轨迹规划是一个高度耦合的非线性问题,一些传统的方法难以直接获取最优结果,例如不等式约束法、经验法等。越来越多的专家学者开始尝试智能优化算法,例如遗传算法、粒子群算法、神经网络和模拟退火算法等。GAO等[5]采用粒子群算法(PSO)对4-3-4多项式插值轨迹规划进行时间优化,该算法参数根据经验设计,方便使用但具有随机性,易于陷入局部最优解。汪婷等[6]采用混合优化遗传算法(GA-DE-SQP)对五次多项式插值轨迹规划进行优化,优化关节空间中的位置-时间序列,该算法收敛速度更快,适应度值更优。连黎明[7]提出一种多变量时间最优轨迹优化方法,以优化机器人各关节运动轨迹达到时间最优,该方法通用性强,能够使机器人运行更加平稳。众多学者在研究机器人时间最优轨迹规划问题时,普遍在关节空间中进行规划,无法可视化机器人的末端位置,且求解效率较低,难以完成对机器人末端路径有明确要求的工作任务,例如弧焊、打磨等。
在此,本文以工业机器人为研究对象,提出了一种基于时间最优的位姿同步轨迹规划方法,该方法分为路径插值和速度规划两个部分。路径点位姿通过六维旋量表示,采用共用节向量的B样条曲线插值方法实现笛卡尔空间中路径点位置和姿态的同步;根据参数化的插值曲线方程,考虑机器人关节的速度与加速度约束,通过线性规划计算得到笛卡尔空间路径参数的相平面图,进而求得最优参数速度。最后利用雅可比矩阵为机器人各关节分配速度,实现时间最优速度规划。
1 路径插值
平滑的路径插值能有效提高工业机器人的工作性能和使用寿命,使机器人在运动过程中免受因路径插值不连续而造成的猛烈冲击和损坏,以免降低机器人的工作效率。工业机器人末端的路径插值又分为位置插值和姿态插值两个部分。
1.1 位置插值
根据机器人的作业任务需求,对于给定的路径点,进行位置插值十分必要。B样条曲线因其插值平滑、便于修改等优良特性被广泛应用于轨迹规划。
B样条曲线的数学定义为[8]:
(1)
式中:di是控制点,Ni,k(u)是基函数,k是基函数的次数,i是序列标签,u是曲线的参数。基函数是构造B样条曲线的基础,定义在一组参数区间上,由Cox-deBoor递归公式给出:
(2)
在众多B样条曲线中,三次均匀B样条曲线计算简便,能构造各种形状,具有高平滑性和C2连续性。所以本文选用三次均匀B样条曲线进行插值:
(3)
式中:D是控制点向量。由式(3)可知,若已知控制点,则可获得样条曲线的表达式。然而,大多数情况下是根据任务需求给定曲线会经过的路径节点。因此需要通过节点反解出控制点,得到曲线方程。
为防止B样条曲线变化剧烈,考虑将曲线起始和终止节点处的曲率设置为零,即令第一个和第二个、倒数第一个和倒数第二个控制点分别重合。则三次均匀B样条曲线的控制点可以通过式(4)求得:
(4)
式中:Pi(i=1,2,…,n)是路径节点。控制点di与节点pi之间的关系如图1所示。
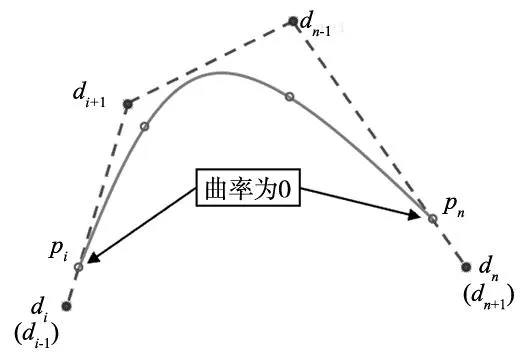
图1 具有自由端点的B样条曲线
此时通过曲线节点反解控制点的公式如下所示:
(5)
将求得的控制点代入式(3),实现用三次均匀B样条曲线在路径节点之间进行位置插值。
1.2 姿态插值
空间刚体姿态的表达方式有旋转矩阵、欧拉角和四元数。其中四元数由于计算复杂度小、不存在万向节锁等优点被广泛应用于姿态插值。其定义为:
Q=q0+q1i+q2j+q3k
(6)
式中:q0、q1、q2和q3是实数,i、j和k是复数的虚轴。写成向量形式为Q=[q0,(q1,q2,q3)]。
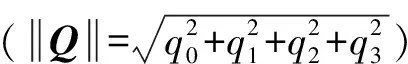
(7)
式中:ω=(u,v,w)是单位旋转轴,θ是旋转角。
根据文献[9],先对四元数取对数,即:
ln(Q)=θω=(x,y,z)=Pori
(8)
式中:(x,y,z)=(θu,θv,θw),Pori是R3空间中的三维点。
此时,可以使用三次均匀B样条曲线插值理论。Pori作为节点P,通过式(5)反解出控制点,再将控制点代入式(3),即可得到每两个节点之间插值点Pori(t)=[x(t),y(t),z(t)],t∈[0,1]。插值点写成旋转角与单位旋转轴相乘的形式:
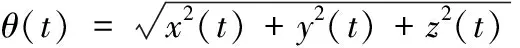
(9)
将式(9)代入式(7),并对方程两边取指数,可得到插值后的单位四元数的实部和复部:
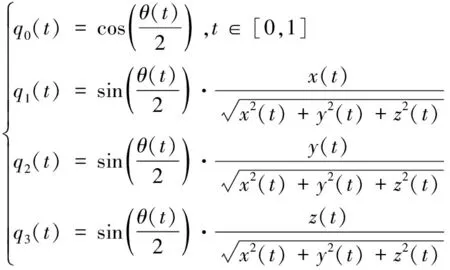
(10)
由式(10)得到一系列路径插值点的姿态,实现对机器人末端的姿态插值,且与位置插值是同步进行的。
2 时间最优速度规划
2.1 路径参数化
针对具有n自由度的机器人系统,其位形空间由n维向量q∈Rn表示[11]。对于在笛卡尔空间中给定的几何路径P,可以表示为函数P(s)。其中,路径参数s∈[0,send],s同时也是关于时间t的单调递增标量函数s:[0,T]→[0,send],因此几何路径可以表示为P(s(t)),t∈[0,1]。因此P的速度和加速度可以表示为:
(11)
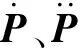
2.2 约束条件
机器人的运动约束是指机器人在运动过程中必须遵守的物理约束。本文考虑机器人的运动学约束,即对机器人关节进行角速度和角加速度的约束:
(12)
关节的导数通过雅可比矩阵映射到笛卡尔空间中[12],如式(13)所示。
(13)
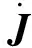
(14)
将式(14)代入式(12)中,对关节角速度和角加速度的约束就转换成了相应的路径参数速度和加速度的约束,即:

(15)
上述式子中,对雅可比矩阵的描述如下:
J=Jp×Jb=
(16)
式中:Jb(q)∈R6×n表示几何雅可比矩阵,r∈R3表示轴角的指数坐标,是关于s的函数。在Jp∈R6×6中,A(r)和Rsb(r)则被表示为:
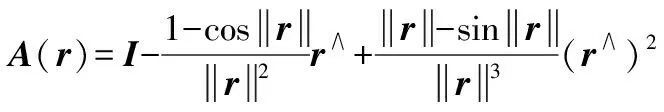
(17)
式中:I是单位矩阵,r∧∈so(3)是向量r相对应的反对称矩阵。
雅可比矩阵J相对于路径参数s的一阶导数为:
(18)
式中:r与s有关,则Jp的一阶路径参数导数表示为:
(19)
式中:Jb是关节值q的函数,Jb(q)的每一列都可以表示为伴随矩阵由式(20)给出:
(20)
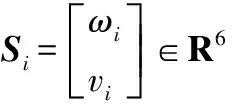
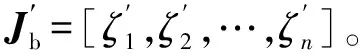
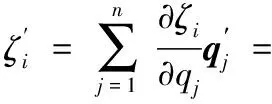
(21)
式中:
2.3 算法实现
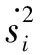
(22)
式中:Δi=si+1-si。
时间最优速度规划算法主要由正向递推和逆向递推两个部分组成。基于控制理论中可达性分析的思想,构建出整个算法的框架如图2所示。
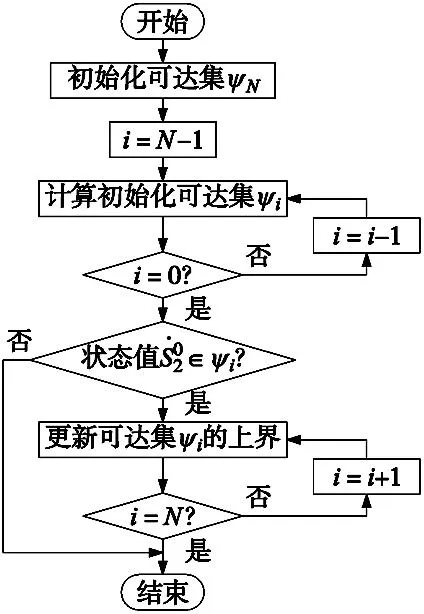
图2 时间最优速度规划方法流程图

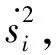
(23)
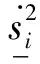
(24)
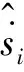
在算法的第一部分逆向迭代过程中,如果出现某一阶段的可达集为0,或者第0阶段的可达集不包含已知期望起始速度,则说明该路径不可时间参数化。第二部分正向迭代在得到可达集的最优状态值后,对控制量进行了重新选择,以“贪婪”的方式更新可达集上界。
3 仿真与实验分析
为验证本文所提出的机器人时间最优轨迹规划算法的可行性。以某公司的6自由度“火弧”机器人为研究对象,采用指数积法(product of exponential,PoE)建立机器人的运动学模型[15]。对“火弧”机器人模型机构简化,当机器人处于零位时进行指数积建模如图3所示。

图3 “火弧”机器人指数积建模
图中:L1=346 mm,L2=600 mm,L3=200 mm,L4=385 mm,L5=925 mm,L6=413 mm。机器人各螺旋轴的参数如表1所示。

表1 “火弧”机器人螺旋轴参数
3.1 路径仿真
对工业机器人末端执行器的位置和姿态插值理论进行验证,设置空间路径节点的位置和姿态信息如表2所示。
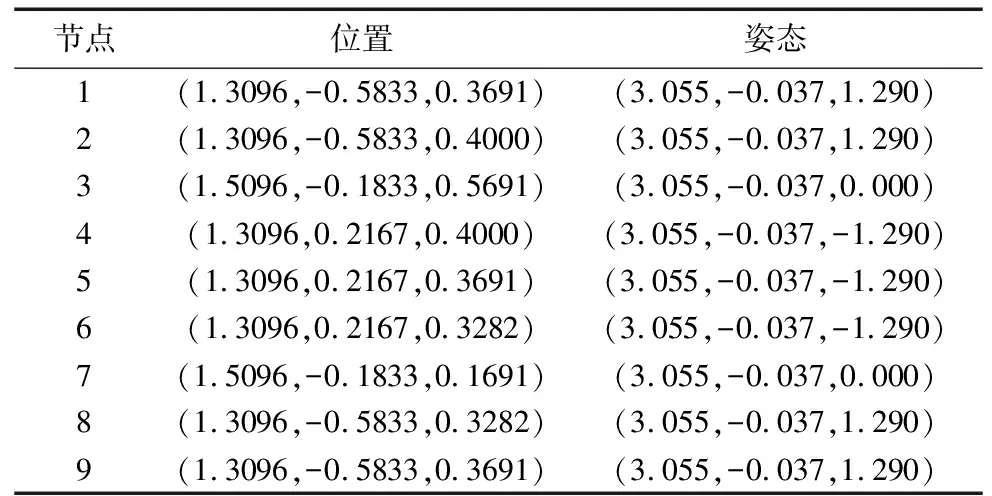
表2 机器人末端执行器路径位姿信息
经过实验,得到插值过程如图4所示,图中稍大的点与长箭头分别表示给定路径节点的位置与姿态,稍小的点表示控制点的位置,连接路径节点的曲线为三次均匀B样条插值曲线,短箭头则表示插值点的姿态。由此实现对机器人末端路径的位姿同步插值。

图4 三次B样条插值过程
3.2 速度规划实验
为验证该算法的可行性,本文基于MATLAB和CoppeliaSim搭建“火弧”机器人联合仿真平台,并对算法进行测试。已知笛卡尔空间的几何路径,对关节信息的约束由表3给出。

表3 运动学约束
通过算法的逆向和正向递推过程,求解出可达集的范围如图5所示。由图可知,更新后的可达集上界在初始可达集范围内,且起始点和终止点均满足约束条件,验证了算法的可行性。

图5 可达集范围
已知路径参数速度和加速度,通过机器人逆运动学以及式(14)可求得机器人运动过程中规划的关节值、关节角速度和关节角加速度曲线,如图6所示。
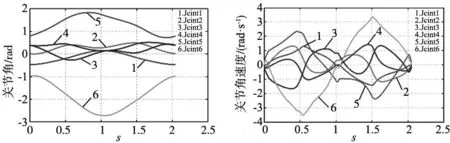
(a) 关节角度 (b) 关节角速度
根据求得的关节信息,在仿真平台上进行测试,运动轨迹如图7所示,由此可见该算法是可行的,并且能够使机器人末端按照给定路径曲线运动,可以完成很多对机器人末端路径有要求的工作任务。

图7 仿真测试运动轨迹
实验结果表明在满足机器人关节运动学约束的条件下,机器人尽可能地选用了最大关节速度或关节加速度,实现了运动的时间最优,提高了机器人的运行效率。
4 结论
针对当前工业机器人时间最优轨迹规划算法的不足之处,提出了一种机器人末端在笛卡尔空间实现位姿同步的时间最优轨迹规划方法。采用B样条曲线和对数四元数插值机器人末端路径点的位置和姿态,基于路径曲线和机器人关节约束,以逆、正向递推求解的方式实现机器人末端路径的时间最优速度规划。搭建基于MATLAB和CoppeliaSim的机器人联合仿真平台进行实验,结果表明机器人可以高效且平滑的经过给定路径节点,达到运行时间最优,实验证明了该方法在工业机器人上应用的有效性。

