阀后管道突扩对控制阀门流阻特性的影响

王 蛟，胡亚安，陈 亮，王召兵

（1.重庆交通大学 西南水利水运工程科学研究院，重庆 400074；2.南京水利科学研究院，南京 210029）

0 引言

在输水调压管道系统中，控制阀门在高压差、大流量条件下很容易诱生空化［1-3］。强烈的空化现象不仅会侵蚀阀体及其管道内壁，还会引发高频振动、声振等不利水力现象并降低阀门的过流性能，显著影响系统的运行效率和维护成本。

基于控流精确、便于电气化控制等要求，一般输水调压系统常采用工业阀门作为控制阀门［4］，一般采用优化阀体内部结构来抑制空化［5］。例如优化球阀阀座型式［6］，在锥形阀阀口设置环形阻止片［7］或优化阀门型式［8］，在活塞阀阀口增加出流套筒［9］等，均能明显提升阀门的抗空化性能，针对特定阀型进行的结构优化普适性较差且制造维护成本较高。在水工阀门领域，常采用突扩廊道体型来改善阀门的抗空化性能［10］。景洪水力式升船机借鉴了水工阀门突扩体防空化技术［11］，研究成果表明，增设突扩体后，阀门的空化强度得到了明显控制，阀后管壁的压力脉动显著降低，但会一定程度地降低阀门的过流能力。对工业阀门流阻特性的研究，与防空化技术研究类似，由于关注重点在阀体内部且受测量手段限制，常采用数值模拟的研究方法［12］，研究阀体自身结构下的流动特性［13-15］，考虑压差［16］、阀内壁面粗糙度［17］、多级套筒［18］等影响因素，进而优化阀座［19］、阀口型式和阀芯结构［20］等来优化阀门的流阻特性［21］，而针对阀后管道突扩对阀门流阻特性影响的研究较少。

已有圆形突扩管道流阻特性的相关研究，多基于理论分析和低流速条件，尚未获取流阻系数与突扩比的定量关系［22］。基于突扩体入流、出流条件为最简单的均匀流情况，JTJ 306—2001《船闸输水系统设计规范》中列出了突扩体突扩段与突缩段的流阻系数半经验计算公式。但一般阀门出流都不是均匀流，采用规范公式计算阀后管道突扩后的流阻系数存在一定误差，为了更加准确地估算阀后管道突扩后的流阻系数，有必要研究阀门实际出流条件下（非均匀入流、出流条件下）的突扩体流阻特性，更加准确地分析突扩体对阀门过流能力的影响规律，寻找突扩体增加阀门抗空化性能与降低过流能力之间的平衡点。基于此，本研究针对适用于高压差、大流量工况的活塞式调流阀与固定式锥形阀，进行阀后圆形突扩管道对阀门流阻特性影响的研究。

1 物理模型设计与验证

1.1 物理模型设计

物理模型设计如图1 所示，主要包括供水供压系统、电气集成控制系统、阀前稳压段、试验阀门、透明观察段、阀后稳压段以及回水系统。试验过程中，通过离心泵和循环水库提供试验水流条件，稳压段主要用于稳定试验段的环境压力；透明观察段采用高强度有机玻璃制造，用于观察阀后水流流态，同时还布置有高精度水压力传感器和水听器，用于分析阀门出流状态以及流场结构；流量通过电磁流量计监测；试验段稳定压力由电子压力表监测。传感器参数特性见表1，传感器测量范围及精度均满足试验要求。

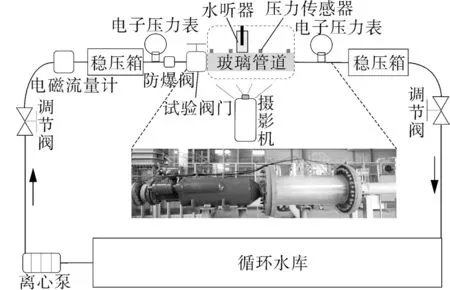
图1 物理模型Fig.1 Physical model

表1 传感器参数特性Tab.1 Sensor parameter characteristics

本研究中试验阀门有两种：一是德国某公司生产的活塞阀，套筒型式为SZ20-30%，与景洪水力式升船机控制阀门主阀的阀型相同；二是武汉某公司生产的固定式锥形阀，管中型（带导流罩）。两类阀门的通径（DN）均为150 mm，如图2所示。

图2 试验阀门Fig.2 Test valves

本研究定制了3 种不同突扩比的圆形突扩管道，采用有机玻璃制作，便于观察阀后水流流态。试验工况见表2，突扩比R 的定义为：

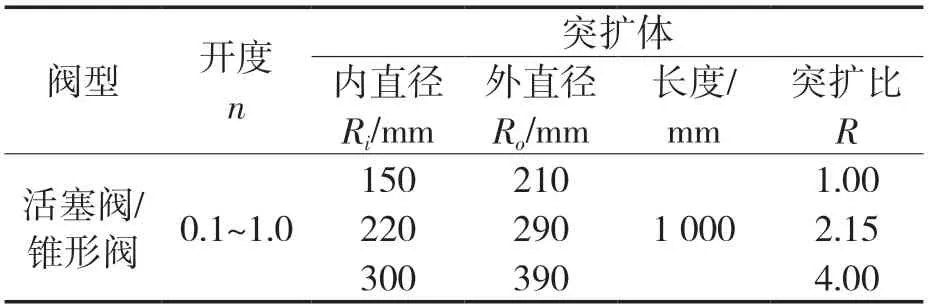
表2 试验工况Tab.2 Test conditions

式中，Ae为突扩管道断面面积；A 为阀门出口断面面积。

1.2 模型验证

王浩等［23］曾对景洪水力式升船机整体缩尺模型进行了物理模型试验，过程中测定了DN150活塞阀的流量系数，本研究以此数据进行模型验证，试验数据与文献数据对比结果如图3 所示，两者吻合较好，说明物理模型试验装置测量结果准确，数据可靠。

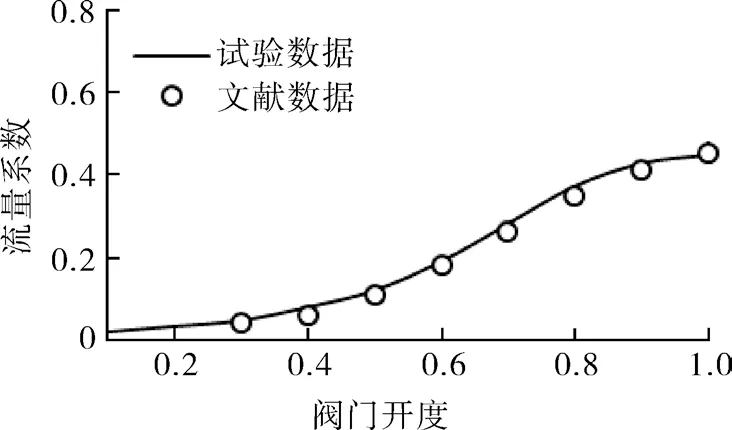
图3 活塞阀流量系数Fig.3 Flow coefficient of plunger valve

2 阀后流态

阀门发生较强空化（空化噪声处于同一量级）、阀后管道采用不同突扩比时，阀后典型流态如图4 所示。活塞阀出流存在一股扭绳型涡带，涡带围绕管道中心旋转，沿水流方向形态基本保持稳定。除涡带外，活塞阀出流水体中还分布着雾状空化，该类空化泡细碎，初生于套筒出流侧孔。水体流经活塞阀壳体与阀芯间层后于套筒处汇聚成束，由于水体分流再汇聚过程的不均匀性以及重力作用，汇聚后的水流呈现漩涡流态，水体中的空化泡受水流流态影响，沿管轴汇聚成扭绳型空化涡带。活塞阀后管道采用不同突扩比时，空化涡带沿水流方向的形态较稳定，但涡带与管壁的间距不断增大。锥形阀出流较为均匀，阀门空化后于水体中可观察到类似于活塞阀的雾状空化，因为锥形阀在阀芯附近也存在与套筒类似的导流孔板，雾状空化正是初生于这些导流孔板的支孔边界处。当突扩比R=1.00 时，可见雾状空化云布满全管，空泡溃灭时直接作用于管壁，容易空蚀管壁并引发振动等不利现象。当突扩比R=2.15时，空化云基本充满全管，但在空泡射流与管壁间会形成不稳定的无空泡水垫层。当突扩比R=4.00时，空泡云与管壁间已形成稳定的水垫层，空化云基本受限于水体内部，空泡溃灭对管壁的冲击可以得到缓冲。阀后突扩管道可以明显减小阀后管壁的压力脉动及振动现象，主要原因之一是水垫层效应。综上可知，锥形阀阀后流态较活塞阀更简单稳定，阀后管道突扩可以限制空化泡的溃灭范围，有利于降低空化引起的管道振动与空蚀破坏。

图4 不同突扩比下的阀后水流流态Fig.4 Flow patterns behind valves with different sudden expansion ratios

3 突扩体对阀门段流量系数的影响

阀后管道突扩可以增强阀门的抗空化性能，但同时也会一定程度地降低阀门的过流能力。对于突扩管道的节流作用，已有半理论半经验公式，但均未考虑阀型、流态等影响因素，仅能作为设计参考，有待进一步优化。本研究针对两类典型工业控制阀门进行了不同阀后管道突扩体试验，考虑了阀型、流态以及水流缩脉等因素的具体影响，通过理论分析得到了阀后管道突扩比与阀门流量系数的关系式。由于分析思路一致，为节约篇幅，下文以活塞阀为例进行分析说明。

不同突扩比下，活塞阀各开度下的流量系数如图5 所示。

图5 不同突扩比下活塞阀流量系数对比Fig.5 Comparison of plunger valve flow coefficient under different sudden expansion ratios

其中，流量系数取值为发生空化前的稳定流量系数。n=0.1～0.5 时，3 种突扩比下流量系数十分接近。表明小开度时，在管道系统中，阀门是输水系统泄流能力的控制性因素，阀门流阻远大于管道突扩的节流作用，阀后采用突扩管道所增加的流阻很有限，对阀门的泄流能力影响很小。n=0.6～1.0 时，随着开度的增加，突扩体型下阀门的流量系数逐渐下降，当n=1.0，R=4.00 时降幅最大，流量系数由0.445 降至0.380，降幅达到14.6%。这是因为在大开度下，阀门流阻明显下降，突扩管道的节流作用相对而言有所增强。

当突扩比由1.00 增加至2.15 时，流量系数最大降幅为12.4%；当突扩比由1.00 增加至4.00 时，流量系数最大降幅为14.6%。说明突扩管道对阀门泄流能力的影响与突扩比有关，随着突扩比的增大，其影响程度在下降。针对阀门段阻力系数可进行理论分析，研究突扩比与阀门段阻力系数的关系，进而可得突扩比与流量系数的关系。

4 流态对突扩段流量系数的影响

流量系数 μ 定义为：

式中，μ为流量系数；Q 为流量；A 为参考断面面积；Pu为阀前稳定压力；Pd为阀后稳定压力；ρ为密度；Σζ为阀门段阻力系数。

从式（2）可知，流动损失是流量系数改变的主要原因［24］。本文试验系统阻力主要由阀门阻力ζv和突扩管道阻力ζe组成。其中，突扩管道阻力主要由突扩段阻力ζex，沿程阻力ζλ和突缩段阻力ζc组成。

由于突扩管道l/d 的比值较大，突扩管道较短，其沿程阻力可以忽略不计，因此：

针对图6 中的1-1，2-2 断面，不考虑位能影响的充分紊动工况，突扩段局部的能量方程为：

图6 突扩管道阻力系数理论分析Fig.6 Theoretical analysis of resistance coefficient of sudden expansion pipeline

式中，v，P 分别为相应断面的流速和平均压力；g为重力加速度。

取两断面作为控制面进行动量分析，控制体所受的外力有：

（1）A1断面的总压力P1A1；

（2）A2断面的总压力P2A2；

（3）突扩管道环面对控制体的作用力P=P1（A2-A1）；

（4）由于未考虑位能，因此重力沿水流方向的分力为0，同时管壁所受的剪力由于与其他力相比很小，因此也忽略。

因此可以列出水流方向的动量方程为：

化简可得：

代入能量方程可得：

利用连续方程及突扩比的定义：

进一步化简，可得突扩段阻力系数与突扩比的关系式为：

以上分析基于均匀出流过程，未考虑阀后流态的影响。本文试验结果表明，阀后流态对突扩管道的阻力系数有影响，阀后水流存在漩涡流等水流结构时，会放大突扩管道的阻尼作用。因此引入一个流态系数m，对上式进行修正，可得：

5 流态对突缩段流量系数的影响

突缩段存在一个缩脉过程，包括一个局部突缩（3-3 与4-4）和一个局部突扩过程（4-4 与5-5）。其中局部突缩过程由于不能得到动量方程，因此无法得到该段阻力系数的解析式，但有相应的经验公式。对于局部突扩过程的分析与前文突扩段相同，本文中突扩段前后管径相等。该段中需定义收缩系数为：

局部突缩的阻力系数经验式为：

参考突扩段的阻力系数解析式，考虑缩脉的影响［26］，则可得出突缩段阻力系数与突扩比的关系式为：

本文突扩管道长度约为阀门通径的6 倍，约等于圆形紊动射流初始段的长度，对叠加效应的影响不大。突扩管道突扩与突缩段的阻尼如何叠加主要取决于水流流态。活塞阀阀后流场结构较复杂，对突扩管道的阻尼作用有放大作用，试验成果表明两段阻尼可以通过线性叠加以增大阻尼：

而锥形阀阀后流场结构简单，近似于等断面出流，两段阻尼可以按下式进行非线性叠加以弱化缩脉现象的影响：

进一步考虑阀门阻力，由流量系数的定义可得整个阀门段的流量系数与突扩比的关系式。

（1）活塞阀：

（2）锥形阀：

基于上式可计算不同突扩比下试验阀门各开度的流量系数理论值，以R=4.00 为例，按规范公式及优化公式计算的流量系数与试验值的对比情况如图7 所示。可见，随着开度的增大，规范计算值与试验值的差异越来越大，最大差异约为8%。优化公式计算值与试验值则吻合较好，最大差异约为1%，说明理论分析是合理的。其中，对于活塞阀：m=1.3，Cc=0.6；对于锥形阀：m=1.0，Cc=0.8。可见，由于活塞阀后流态较为复杂，流态对突扩节流阻尼有放大作用，在突缩段的收缩程度也更大，将放大缩脉现象的影响。

图7 阀门流量系数理论值与试验值对比Fig.7 Comparison of theoretical value and test value of flow coefficient

6 结论

（1）阀后管道突扩能在空化泡与管壁间形成水垫层，将大部分空化溃灭限制在水体内部，从而降低空化引起的管壁振动与空蚀破坏。试验条件下，突扩比为4.00 时，水垫层已较为稳定。

（2）阀后管道突扩会一定程度地降低阀门的过流能力，通过理论分析可以得到管道突扩比与阀门流量系数的关系式。试验结果表明，阀型、阀后流态与水流缩脉均对阀门流量系数有显著影响，并可通过管道突扩比实现量化。拟合关系式中的突扩段流态修正系数m 和突缩段收缩系数Cc均与阀门类型密切相关。规范计算值与试验值的最大差异约为8%，优化公式计算值与试验值最大差异约为1%，说明改进后的突扩体流阻系数公式的计算精度较规范公式有所提高。

本文的研究结果对高压差、大流量调流调压管路的设计具有较强的指导意义和参考价值。