DN100 型物联网流量型平衡阀性能试验研究

黄永琪，王福乔，白 烨，姚国鹏，王保民，彭 烁

（中国华能集团清洁能源技术研究院有限公司，北京 102209）

0 引言

我国的供热系统庞大，极易造成二网不平衡或者冷热不均的问题［1-2］，平衡阀是调节二网平衡的关键设备。国外对平衡阀的研究较早。Taylor 等［2-4］阐述了空调水系统中平衡阀的正确选择的重要性、基本原理及几种典型系统中的平衡阀的选型方法。我国平衡阀的研究较国外稍晚。康金松［5］从理论上明确了平衡阀的选择原则，总结了安装平衡阀后，达到的节能和增效的效果。沈新荣等［6-8］结合CFD 对平衡阀进行数值模拟，根据数值模拟结果，改进了现有平衡阀初步设计的结构参数。目前供热二网普遍采用基于温度传感反馈的温度型平衡阀进行调控，该阀门在实际应用中仍存在不足，主要表现为阀门开度的变化与温度反馈的滞后，导致二网平衡调整周期长，易出现温度来回波动。本文提出一种基于流量反馈的流量型平衡阀，采用流量作为直接的平衡依据，具有即时性、直观性、高分辨的特点［9-11］。

以口径为DN100，压力范围为0.3～0.8 MPa，介质温度范围为-5～120 ℃的物联网流量型平衡阀作为研究对象，采用CFD 进行流场计算，对物联网流量型平衡阀的3 类阀芯形状（W 型，V 型，O 型）进行数值模拟，得到不同阀芯的阀门开度-流量模拟结果，研究不同阀芯对应的压力场轴向变化，根据数值计算结果确定适合该口径平衡阀的阀芯形状及取压点位置。

图1 3 种形状阀芯（W 型，V 型，O 型）Fig.1 Three types of valve core（W，V，O）

根据确定好的阀芯形状和取压点位置制造物联网流量型平衡阀样机，利用试验平台对该阀门进行流量标定，试验得出阀门开度、阀门进出口压力与流量之间的函数关系，形成一组特性曲线，并对数值计算和试验结果进行比对分析，根据对比分析结果，论证该阀门在供热二网平衡中的适用性。

1 结构及调节原理

物联网流量型平衡阀的主要部件如图2 所示，主要由阀体、阀芯、阀杆、阀座、阀座弹簧、阀杆轴套、取压孔、电动执行机构、电路板及电子部分等组成。

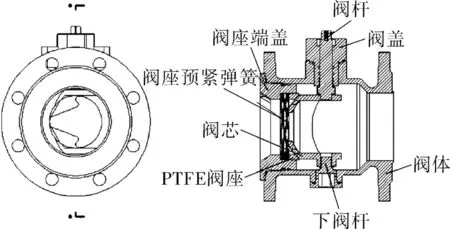
图2 物联网流量型平衡阀结构Fig.2 Structural diagram of IoT flow balance valve

物联网流量型平衡阀的调节原理是通过在阀体进出口安装压力传感器测量进出口压差，根据阀门开度对应的流量系数利用伯努利方程式即可计算出当前流量，通过流量的变化及时进行二网调节，即可实现二网平衡。

2 数值方法验证

2.1 计算模型

本文采用Realizable k-ε 湍流模型［12］，该模型在CFD 界被普遍使用，其湍动能k 和湍动耗散率ε对应的输运方程分别为：

该模型使用不同的涡流黏度公式，基于湍流雷诺应力的几个可实现性质做约束，这意味着涡流黏度系数Cμ是局部流动参数的函数，而不是Standard k-ε 模型中的常数。该模型在ε 方程中引入了时均应变率Eij，且另外增加了时均转动速度张量，确保模型在雷诺压力中有数学约束和湍流的连续性［13］。此外，该模型还显著改善了圆形射流的预测扩散速率。

2.2 计算流道及网格划分

为获得较好的计算结果，对球阀的结构做了适当简化，在保证流道尽量不受影响的同时，减少复杂形状对计算收敛性的干扰。

CFD 模拟前对三维模型流道进行设置，如图3所示。为保证计算结果合理性，根据管道流量测量的一般要求，对阀前、阀后设置直管段，阀前取当量直径的6 倍（即-0.6 m），阀后取当量直径的10 倍（即1 m）。

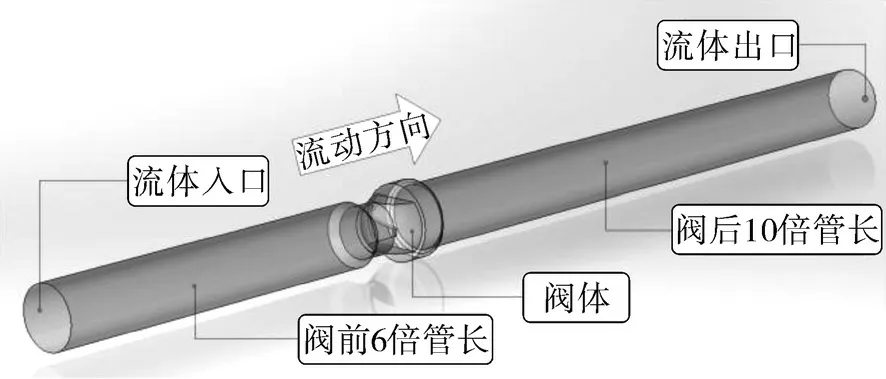
图3 直管段示意Fig.3 Schematic diagram of straight pipe section

为简化计算，将XZ 平面作为对称平面，以减少网格数量；采用正六面体结构网格（Structured mesh）对模拟区域进行划分。为提高计算精度，在阀门主体部分，进行网格加密。从管道入口到阀门的入口法兰的网格放大系数为0.97，阀门出口法兰到管道出口的网格放大系数为1.03。

对项目特征进行提取后，分别在不同网格密度时，模拟W 型阀门65%开度，流量为45 t/h 的典型试验工况。对各网格密度的管道出入口压差做统计，进行网格无关性检验［14］见表1。

表1 网格无关性检验tab.1 Grid independence test

方案1 为初始方案，后续方案均为在初始方案的基础上进一步加密网格得到。从表1 可见，在方案4 之后，进一步加密网格所得到的结果变化值始终在5%以内波动，因此从保证计算效率和结果可靠性的角度出发，认为方案4，总网格数量为70 万时，结果相对稳定，网格无关性较好。取方案4 的网格密度作为后续试验的基础，即本项目的模拟网格数量共70 万个。

2.3 计算边界

本文模拟计算中采用Realizable k-ε 湍流模型，壁面边界，壁面粗糙度为0.005 m，管径为0.1 m；入口压力为0.8 MPa，入口直管段长度为6 倍管径；出口压力为0.7 MPa，出口直管段长度为10 倍管径；以水为工质，流量为45 t/h，流体温度和环境温度为20 ℃，管道内平均流速为1.59 m/s，雷诺数为157 579.15。其中水的动力黏度为0.001 01 Pa·s，运动黏度为0.000 001 01 m2/s，密度为1 000 kg/m3。

2.4 计算结果分析

2.4.1 压力场轴向分布的计算

W 型、V 型、O 型阀芯压力场轴向分布分别如图4～6 所示。

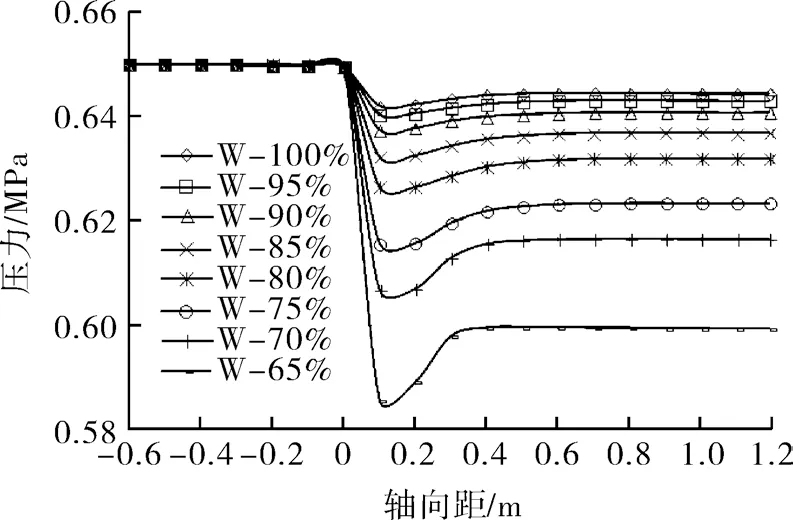
图4 W 型阀芯压力场轴向分布Fig.4 Distribution of pressure field of W type valve core along the axis

图5 V 型阀芯压力场轴向分布Fig.5 Distribution of pressure field of V type valve core along the axis

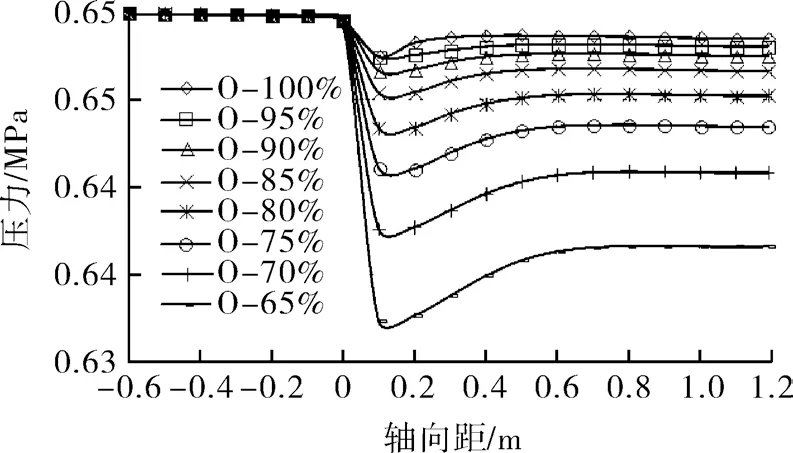
图6 O 型阀芯压力场轴向分布Fig.6 Distribution of pressure field of O type valve core along the axis

从图中可知：（1）3 种阀芯都存在进、出口取压点越接近0 m 处，压力场越不稳定的问题，因此设计一体阀时无论是哪种阀芯，进、出口取压点位置设在阀体上两端为佳。

（2）W 型阀芯的压差最大，即节流效果最强，V 型阀次之，O 型阀芯最弱。

2.4.2 开度-通流面积趋势

计算各阀芯形状在不同开度时对应的直径和开口面积，此处开口面积为通流方向的截面积。

各阀芯开度-面积趋势如图7 所示。从图中可以看出：（1）当需要的调节阀的流量系数较小时，阀口处的流通面积较小，故此时阀体内流道形状对调节阀的流量特性影响不大，甚至可以忽略。但当需要的调节阀的流量系数接近于阀体的流量系数时，意味着阀口处的流通能力接近于阀体的流通能力。

（2）W 型阀芯的通流面积的变化与V 型、O型阀芯的通流面积的变化有特征上的区别，如图7 所示，V 型、O 型阀芯的通流面积的变化偏线性，而W 型阀芯通流面积变化偏指数型，W 型阀芯这种截面变化可以更好地改善阀门的流通特性，具有更好的流量控制能力。

图7 开度-通流面积变化特性Fig.7 Variation characteristic of opening degree with flow area

2.4.3 开度-流量特性曲线

各形状阀芯开度-流量特性曲线模拟计算结果汇总如图8 所示。

阀门流量特性数学表达式为［15］：

式中，Q 为阀门某一开度时流量；Qmax为阀门全开时流量；h 为阀门某一开度时行程；hmax为阀门全开时行程。

根据式（3）及图8 绘制阀门流量特性曲线，如图9 所示。从图中可以看出，该阀门符合等百分比型调节阀流量小时流量变化慢，流量大时流量变化快，具有小流量可精细调节、大流量可快速调节的特点，符合等百分比流量调节特性［16-17］，即这3 种阀芯的流量特性曲线呈等百分比型，具有较好的可调比，适用于调节阀调节特性。

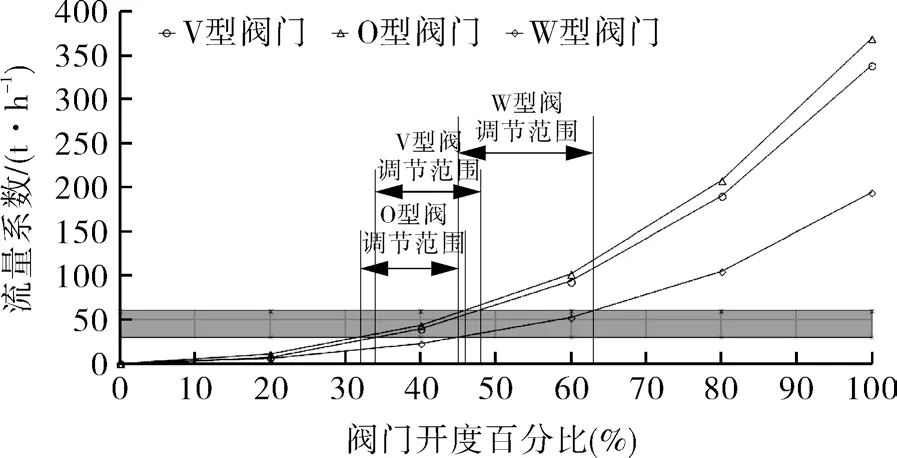
图8 阀门开度-流量特性曲线Fig.8 Opening degree - flow characteristic curve

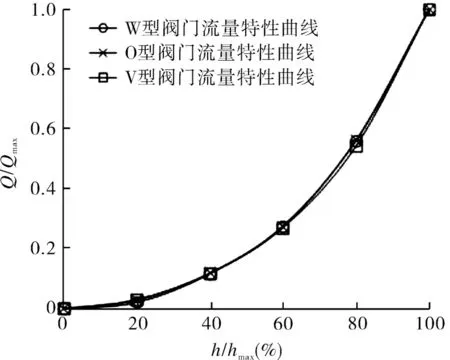
图9 流量特性曲线Fig.9 Flow characteristic curve

该口径阀门的流量调节范围为30～60 t/h，如图8 阴影区域所示，对照3 个阀门的开度映射，可知：

（1）O 型阀门的开度在32%～46%之间，V 型阀门开度在34%～48%之间，W 型阀门开度在45%～63%之间，可知，W 型阀门在对应流量下的调节范围最大，调节能力最强；

（2）在流量中位数为45 t/h 时，O 型阀门开度值为40%，V 型阀门开度值为42%，W 型阀门开度值为54%，W 型阀门在流量中位数下的阀门开度更接近中间位置，流量适配性更好；

（3）从压力场轴向分布特性和流量适配性来看，W 阀芯具有更好的调节能力，更好的流量控制能力，在本文中选取W 型阀芯调节阀进行制造并用该阀门进行试验。

3 试验验证

3.1 试验系统

试验台主要由3 大系统组成，如图10 所示。（1）管路系统，在管路内形成可控的流动，由储水箱、循环水泵、稳压罐、电磁阀、被测阀门、管路等组成；（2）控制系统，负责测试参数信号的测量、信号的转化、数据的采集和传输，同时对管内流动进行控制和监测，由压力传感器、信号执行器、数据采集卡、通讯串口、计算机、变频电控柜等组成；（3）软件系统，实现调控、数据的实时存储、测试结果输出等功能，由参数输入界面、功能测试界面及报表输出等可视化界面组成。该试验台可模拟阀门实际使用工况，能够更准确地测试出阀门相关的特性曲线。

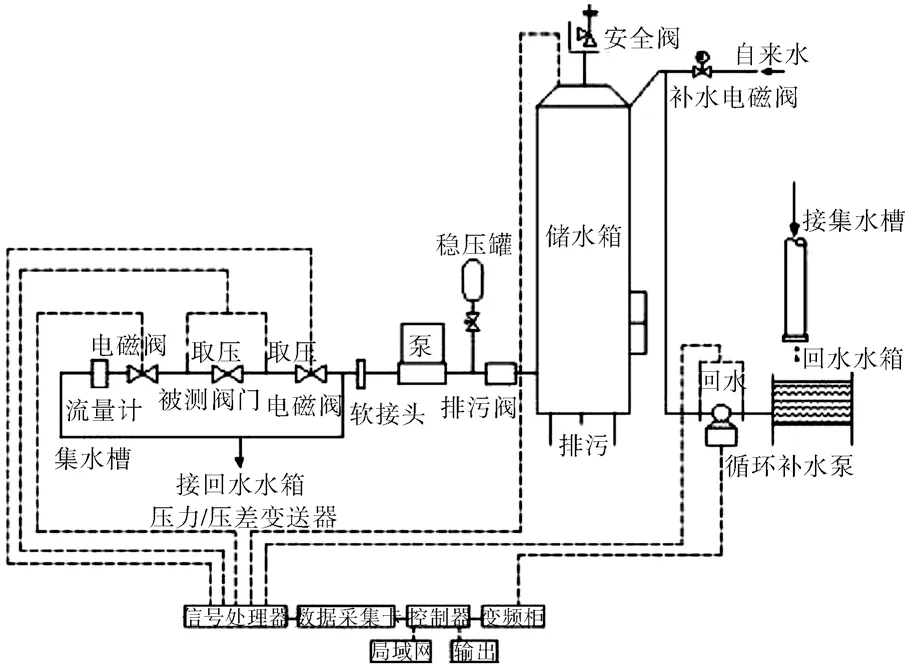
图10 试验台系统Fig.10 Schematic diagram of the test bench system

3.2 试验原理及方法

根据CFD 数值模拟可知，W 型阀芯具有更好的调节能力，因此选取W 型阀芯进行样机制作，并对其进行流量-压差试验，通过流量-压差试验，得到流量特性曲线。

依据GB/T 30832—2014《阀门流量系数和流阻系数试验方法》进行试验。

试验方法及过程：（1）取压点分别设在试验台的管道上阀门前当量直径的10 倍处与阀门后当量直径的10 倍处；（2）阀门开度5%～100%，分别按照开向和关向2 个方向进行试验，开向依次从5%～100%，关向依次从100%～5%，每个方向暂定为20 个开度（每5%一个）；（3）试验数据通过中枢系统存储并输出。

3.3 误差分析

本试验中主要用到的试验仪表见表2。

表2 试验误差分析Tab.2 Analysis table of test errors

对于流量和压差参数，误差精度均为±0.5%，满足精度要求。

对于流量系数Kv，其误差计算式为：

式中，Skv为流量系数的误差；SQ为流量计的误差；SP为压差变送器的误差。

最终，算出流量系数的误差为0.56%，满足精度要求。

3.4 试验数据分析

根据试验数据绘制流量-压差曲线，如图11，12 所示。

图11 5%～100%流量-压差曲线Fig.11 5%～100% flow-pressure difference curve

图12 100%～5%流量-压差曲线Fig.12 100%～5% flow-pressure difference curve

流量系数Kv按下式计算［18］：

式中，Kv为流量系数；Qv为流量，m3/h；ρ为水密度，kg/m3；ρ0为15 ℃时的水密度，kg/m3，常温时ρ/ρ0比值取1；ΔP 为压差，kPa。

根据式（5）和图11，12 的流量-压差曲线，计算Kv值。

由于数据表的不连续性，所以要考虑开度在2 个典型值之间的数值计算问题。中间的数据要采用插补方法进行估算，插补估算将根据实际阀门的流量特性分为两种插补计算方法：线性插补估算、等百分比插补估算。根据前面数值计算中可以得知该阀门流量特性为等百分比型，故在此次试验中采用等百分比插补估算为：

式中，y 为当前开度的Kvx值与最大开度的Kv100的百分比；R 为底数；x 为阀门实际开度的百分比。

查表可知Kv1，Kv2，Kv100，x1，x2，已知当前开度为x，且x1＜x＜x2时，求当前开度x 下对应的Kvx值。

按照等百底数R 线性分布的原则，即：

式中，Rx为当前开度x 下的等百底数。

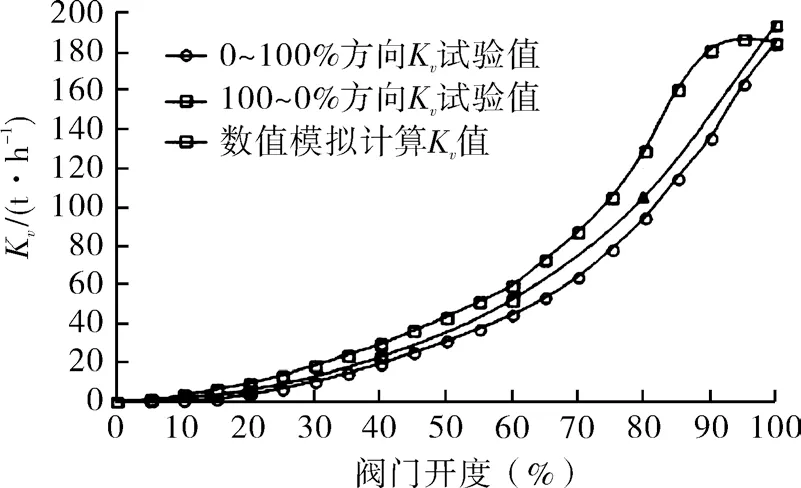
图13 阀门流量开度计算值与实测值对比Fig.13 Comparison between the calculated and the measured values of flowrate and opening of the valve

从图中可以看出：

（1）模拟计算Kv值（即W 型阀芯阀门流量特性曲线模拟计算结果）介于实测值0～100%方向Kv值与实测值100%～0 方向Kv值之间，趋势基本一致，试验值充分论证了数值模拟计算该阀门符合等百分比阀门特性的结论，说明该阀门具有较好的可调节性。

（2）开度越大时，开向和关向Kv值相差也越大（回差较大），主要原因是阀门各个零件累加起来的总机械间隙较大和零件之间填料紧导致的摩擦大。

4 结论

（1）一体阀取压点位置设在阀体上两端；3 种阀芯流量特性都呈等百分比流量调节特性，都有良好的调节性，都适用于做调节阀阀芯。

（2）根据压力场轴向分布特性和流量适配性，对于口径DN100 阀门，W 型阀芯具有更好的调节能力，更好的流量控制能力。

（3）W 型阀门符合等百分比阀门特性，具有较好的可调节性。

（4）试验中发现该阀门存在回差较大的缺点。主要原因是阀门各个零件累加起来的总机械间隙较大和零件之间填料紧导致的摩擦大。可通过加工时提高零件加工精度，装配时调整好装配精度，零件之间填料选用摩擦系数小的材料来减少回差［19］。