基于H∞算法的燃气轮机振动主动控制

刘孔忠，宁智轶，李有佳，陈玲玲，赵利达，浦栋麟，孟瑾，阮鹏，陈凡

（1.中海石油（中国）有限公司海南分公司工程建设中心，海口 570100；2.中国航发燃气轮机有限公司无锡分公司，江苏 无锡 214125；3.中国航发燃气轮机有限公司，沈阳 110000；4.华中科技大学，武汉 430074；5.江苏集萃华科智能装备科技有限公司，江苏 无锡 214174）

0 引言

燃气轮机是一种利用轴系零部件高速转动，将燃料的化学能转换成机械能的动力设备，其整体具有结构紧凑、集成度高、能量利用率大等特点，在工业生产中得到了广泛的应用，包括但不限于机车和船舶的动力供应、工业发电等[1]。目前，随着我国制造业水平的不断提升，国内燃气轮机的制造技术取得了长足的进步，但国内燃气轮机的机动性设计和可靠性设计水平与国外相比还有很大差距。振动问题是燃气轮机常见的一种故障，具有潜伏性、不确定性和复杂性的特点[2]，这使得其监测和控制更加困难。剧烈的振动将带来噪声升高、热负荷增大、降低机械寿命和意外停机等问题，如果不及时进行监控和处理，将导致巨大的经济损失。因此，燃气轮机的振动抑制已成为该领域亟待解决的热点问题。

导致燃气轮机振动的原因主要有以下几种：1）系统热变形引起的振动。在燃气轮机启动和变工况过程中，热载荷的不均匀冲击将使转子及轮机附近温度分布不均，这将导致转子轴向产生不同的膨胀量，这些膨胀量在转子工作时将会转化成明显的热振动现象，影响轮机部件的使用寿命。2）因装配误差、动平衡精度差、加工误差及设备材料属性随温度变化等多种原因导致的整体质量分布不均衡、系统轴系不对中，以及高速转动下产生的离心力都将成为引起燃气轮机振动的原因。3）因部件结构和材料属性不同导致的固有频率的差异，从而引发的复杂的共振现象。4）长时间的运行使轮机部件松动、老化等，会导致轮机振动，剧烈的振动又会加剧系统不稳定的状态，从而进入恶性循环，使振动现象愈演愈烈。

振动的抑制是指针对装置的振动形态及参数，采取相应的控制措施，以达到减振效果。截至目前，绝大多数学者振动抑制的方法可以总结为吸振、隔振、消振和阻尼减振4种方案。人们根据这种4种主要方案，运用不同手段对燃气轮机的振动监测和振动抑制进行了大量的研究。Rahmoune等[3]开发一个使用动态神经网络方法的故障检测系统，对燃气轮机的振动行为进行检测，预防故障发生。Annaswamy等[4]在推导出燃烧室的火焰传递函数的基础上，通过设计线性二次型高斯调节器对热声耦合振荡进行抑制，取得了较好的控制效果。Zhao等[5]提出了通过采用Helmholtz共振器的调节控制，从而改变Helmholtz颈部面积，实现了抑制不稳定燃烧导致的燃烧器振动。Zargar[6]提出了智能推理和案例研究的方法，来减小燃气轮机主轴的振动。国内也开展了相关的试验研究，针对热振动问题，徐宁[7]通过建立燃气轮机空间热载荷分析模型，得到热载荷分布函数，从而通过控制载荷分布及温变曲线，使轮机热致振动得到抑制。王宝辉[8]通过对燃气轮机的工作环境进行分析，结合轮机结构的基础上，提出了设备的隔振方案和优化方案对振动进行处理，防止其影响周边环境。清华大学[9]为构建燃气轮机工作过程中的整体燃烧系统，建立了燃气轮机燃烧动力学试验平台及其对应的动态测量系统。北京航空航天大学[10]为建立贫油预混燃烧模型，建立了燃气轮机的燃烧试验台，并试图通过被动控制的方法抑制燃烧过程中产生的不稳定现象。从控制方案分析，现阶段该领域的大部分研究还集中在振动的检测、振动的被动控制等方面，对振动的主动抑制控制方案的研究较少；从研究对象分析，现阶段的研究主要集中在燃气轮机的内部零部件的振动抑制问题上，如转子、轴承、燃烧室等，对于全尺寸燃气轮机主动控制的试验研究相对较少。而机匣作为机组多种部件的连接件和支撑件，是整体机组稳定运行的保障，机匣的振动易受很多部件的影响，因此其动态特性分析和控制方案设计比单一的零部件更为复杂。

针对以上问题，本文采用线性化电磁致动器作为主动控制部件，其指令输入电流和输出力之间具有线性关系，更有利于控制器设计以及理想控制效果的实现[11]；同时，采用H∞主动控制方法对燃气轮机的整体机匣进行振动抑制的研究，该控制方法对于多输入输出的控制系统表现出良好的鲁棒性[12]。本文提出的利用电磁致动器与H∞控制算法的燃气轮机机匣振动主动控制方法，可以显著提高燃气轮机机匣振动稳定性，使其振动得到大幅抑制。

1 振动主动控制系统组成与工作原理

1.1 系统组成

燃气轮机工作过程的本质是将天然气的化学能通过膨胀做功的方式释放，转化为其高速转动的动能，并对外做功。

图1所示为燃气轮机振动主动控制系统的原理。燃气轮机工作流程如下：进入燃烧室的燃料与通过压气机压缩后的高压空气在燃烧室燃烧，将燃料的化学能转化为气体内能的同时，生成高温、高压烟气，巨大的压强可以将气体的内能转变为气体的动能，从而在燃烧室的出口高速喷出，推动燃机涡轮叶片转动。燃气透平做功的能量去向主要分为两部分：一部分用于驱动压气机工作，继续产生高压气体，维持燃烧室工作。另一部分做功输出则用来驱动机械设备，例如发电机等，这部分能量可以认为是燃气轮机工作的有用功。除此之外，为提高燃气轮机工作效率，产生了很多能量多级利用的方案，由于从燃气轮机排出的烟气温度很高，仍然具备很高的能量，燃机烟气余热依然具有很高的利用价值，在工业上常常使其在燃气-蒸汽联合循环电站中把水加热成蒸汽去推动蒸汽轮机，带动发电机发电，用以提高电厂整体效率。

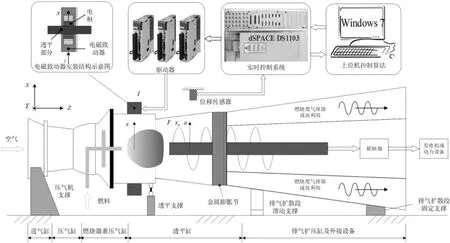
图1 燃气轮机振动主动控制系统结构示意图

本文将主要通过振动控制仿真研究的形式验证所提出的基于H∞控制算法的燃气轮机振动主动阻尼方案在振动主动控制方面的有效性，为以后的实验研究奠定前期理论基础。后期实验系统可参考图1所示的示意结构进行搭建，在PC端通过Matlab/simulink程序设计好H∞控制算法模型，并下载到dSPACE系统中进行实时控制，通过驱动器输出激励电流驱动电磁致动器对机匣进行振动主动抑制。

1.2 振动主动控制工作原理

本文选择H∞最优控制方法进行控制器设计，因为H∞最优控制方法在实现最优频响整形性能稳定方面具有优势。所采用的电磁致动器具有径向（x,y）两个方向上的自由度，可以在对应自由度方向上产生电磁力用于振动主动控制。在整个燃气轮机工作的过程中，透平部分作为燃料反应发生空间，其所承受热载荷巨大，振动现象明显，振幅较大。燃气轮机透平部分的振动信号可以采用位移传感器或者加速度传感器进行采集。考虑到电磁致动器的安装稳定性、测试的便捷性及安全性，电磁致动器计划安装在透平部分的圆柱形部件外，结构示意图如图1所示。

其中，F为导致燃气轮机机匣振动的扰动力，通过放大器将控制电流I施加到电磁致动器上，在电枢处产生磁力，来抑制机匣振动。xa、a分别为透平部分位移传感器所在位置处的位移信号及加速度信号。x为电磁致动器位置的位移信号。

2 系统建模

假设机匣在径向x、y方向上动力学特性不耦合。我们取x方向的弯曲模态对系统的动力学特性进行分析。假设从电流I到位移x、xa的开环传递函数分别用GxI、GxaI表示，从扰动力F到位移x、xa的开环传递函数分别用GxF、GxaF表示。考虑到燃气轮机机匣作为整体机组的固定设备，其外力和振动特性受多种其他零部件的影响，通过对多个其他零部件的动力学特性进行分析，并兼顾机匣整体的材料、尺寸等固有的材料属性，结合建模仿真结果，选取表1所示系统动力学参数，并得到燃气轮机的频响函数曲线如图2所示。

表1 系统不同模态下的相关参数

图2 系统的频响曲线

扰动力、电流与机匣振动位移之间的频响函数表明，该机匣具有三阶模态，其中，在156 Hz时的第一阶模态刚度最弱，在587 Hz和987 Hz的第二、第三阶模态其刚度也较弱。

典型二阶系统的传递函数为

我们可以得到从控制电流I到机匣位移信号x、xa的传递函数为：

其中，ωni=2πfni和ξ分别为模态频率（rad/s）和阻尼比，kxIi、kxaIi分别为系统GxI和GxaI的第i阶模态刚度。

燃气轮机的动力学模型为：

式中：kxFi、kxaFi分别为系统GxF和GxaF的第i阶模态刚度。

根据上式，可以得到在电流I和扰动力F的共同作用下，燃气轮机机匣的位移信号x、xa的传递函数表达式：

3 H∞控制器设计

机匣主动阻尼的最终目标是抑制机匣的振动，延长整体机组的使用寿命。因此，控制器设计的主要目标是在驱动器许用电流的约束范围内提高机匣所有振动模态的动刚度。

3.1 控制系统架构

本文选择H∞最优控制方法进行控制器设计，因为H∞控制器对于多输入输出的控制系统表现出良好的鲁棒性，并且可以通过加权函数的合理设计实现对被控系统的回路成形控制。控制系统框图如图3所示。

图3 控制系统设计框图

在控制方案中，采用燃气轮机匣的加速度a作为反馈信号，通过加权函数WI对从扰动力F到控制电流I的闭环频响函数进行约束，以避免驱动电流饱和。利用加权函数Wx对从扰动力F到位移xa的闭环频响函数进行约束。ZI和Zx为经过加权函数后的输出变量，K（s）为利用H∞优化算法设计的控制器。

3.2 加权函数设计与调试

加权函数WI和Wx可采用如下传递函数形式：

式中，Kp、f1和f2为加权函数的调谐参数。

通过对加权函数进行调谐，使从扰动力F到机匣透平部分位移xa的闭环频响函数的峰值在驱动器电流许用范围内尽可能得到衰减。图4显示了加权函数（Wx）-1和（WI）-1的对F到xa的闭环传递函数TxaF及F到I的闭环传递函数TIF的影响。为了降低TxaF在固有频率处的峰值，可以同时调整Kp、f1和f2的值，以降低TxaF峰值频率区域附近（Wx）-1的幅值。同样地，（WI）-1的幅值可以在TIF的峰值频率区域附近减小，以抑制TIF的峰值。当一阶加权函数不能提供良好的控制性能时，可以在调优过程中使用二阶加权函数。适当选取Kp、f1和f2的值可以使｜TxF（jω）｜，｜TIF（jω）｜的峰值部分在主动控制过程中得到抑制，进而达到主动阻尼的效果。

图4 加权函数频响曲线示意图

3.3 广义被控对象建模

为了利用H∞优化算法设计主动阻尼控制器K（s），需建立广义被控对象的状态空间模型。

首先，建立燃气轮机机匣动力学模型的状态空间方程：

式中：qx是状态向量，Ap、Bp、Cp、Dp为系统状态矩阵，u为系统输入。

同样地，由加权函数的传递函数也可以推导出权函数的状态空间方程如下：

式中：qWI和qWx为状态向量。

状态空间模型和系统矩阵可以由式（1）～式（6）求出。

根据上式可以得到H∞控制的广义被控对象的状态空间模型为：

3.4 控制器设计

建立了广义被控对象模型后，将设计控制器K，使闭环控制系统稳定，且从F到z（z=[zizx]T）的闭环传递函数TzF的H∞范数最小。这个H∞最优控制问题可以用线性不等式LMI算法来求解（可通过Matlab中的hinfsyn函数来实现）。合成的H∞最优控制器的传递函数为

其中，k为控制器的阶数，控制器参数为ai、bi（i=0，1，2，…，k）。最终求得该控制器的阶数为9阶控制器，控制器参数如表2所示。

表2 控制器参数

4 主动阻尼仿真实验结果

对燃气轮机机匣在无控制状况和主动阻尼状况下的动态特性进行仿真，得到的对应的频响函数曲线如图5所示。

图5 扰动力F到位移xa的闭环频响函数曲线

从仿真结果来看，在156 Hz的第一阶模态完全被控制器抑制，在587 Hz附近的第二阶模态和987 Hz附近的第三阶模态同样获得了较好的阻尼效果。可见，所有控制情况下的动态刚度都有很大的提高。该控制方案表现出很好的主动阻尼性能。

从扰动力F到控制电流I的闭环频响仿真结果如图6 所示。可以看出，在987 Hz的第三阶模态比前两阶模态更难阻尼，因为它需要更高的控制电流。这就说明，如果振动发生在机匣的第三阶模态频率附近，较大的振动将会导致非常高的控制电流，这将可能导致驱动器电流饱和。由于电流的限制，导致第三阶模态很难被完全阻尼，但在控制方案下，第三阶模态的动刚度仍然从0.060 N/μm提升到了0.079 N/μm，而第一、二阶模态的动刚度提升效果更佳。

图6 从扰动力F到控制电流I的闭环频响函数曲线

在通过频域内的对比分析验证控制方案的有效性后，我们以156 Hz频率附近的振动为例，对于燃气轮机的振动主动控制开展了时域仿真实验研究，以对比主动阻尼开启和关闭情况下的振动情况，仿真实验结果如图7所示。

图7 时域振动控制仿真结果

从仿真结果可以看出，在无控制的状况下，燃气轮机的振动范围在±1.8 mm左右，在开启主动阻尼的情况下，其振幅减小到±0.1 mm左右，振动量级比控制未开启状况下降低了90%以上，具有良好的振动抑制效果。

5 结论

采用电磁致动器对燃气轮机机匣进行主动阻尼，以机匣透平处的加速度作为反馈信号设计了H∞最优化控制器，开展了振动主动阻尼研究工作与仿真实验。结果表明，所提出的振动主动阻尼控制策略显著提高了燃气轮机系统的动态刚度，从而减小了其机匣的振动幅度，为燃气轮机的振动主动抑制提供了理论支撑。