基于双矢量的三电平PFC 中点电位平衡无权重型模型预测控制
高曼曼(中国电源学会会员),龙珊珊,王 飞,党超亮,3(中国电源学会会员)
(1.石家庄理工职业学院智能制造与技术学院,石家庄 050200;2.西安理工大学电气工程学院,西安 710054;3.西安交通大学电力设备电气绝缘国家重点实验室,西安 710049)
随着电动汽车行业的快速发展,用户对电动汽车充电桩的可靠性和电能质量提出了更高的要求。三相三电平整流器作为电动汽车充电设施的核心组成部分,其性能决定着网侧电能质量和蓄电池的使用寿命。三相Vienna 整流器[1]具有成本低、网侧电能质量好的优点,已广泛应用于汽车充电领域。诸多学者将模型预测控制算法FCS-MPC(finite control set model predictive control)应用于变流器的控制策略上[2-4],凭借其具多目标跟踪、动态响应快的优点,已取得良好的控制效果。
目前,针对应用在三电平变换器的模型预测控制已取得了一些研究进展。对于三电平变换器具有的中点电位不平衡问题解决方案一般有2 种方法:第1 种方法是根据FCS-MPC 易于实现多目标跟踪的优势,通过在价值函数中引入中点约束项的方式来实现中点电位波动抑制,由于此方法主要存在的问题是权重因子与控制变量之间没有明确的数学关系,其设计需要反复整定和试凑[5-6],这将带来极大的不便;第2 种方法是利用冗余小矢量来控制直流侧中点电位的波动[7-9]。文献[7-8]通过调整冗余小矢量的动作时间,使得中点电位趋于平衡;文献[9]提出了一种基于冗余短矢量预判的模型预测电流控制方法,上述方法实现了中点电位平衡并有效避免权重因子难以选取问题,凭借单目标函数就可实现系统控制,但其遍历的矢量集个数较多。此外,FCS-MPC 策略通过价值函数来评估出最优矢量,在采样周期内作用于此矢量会带来网侧电流纹波较大的问题,这是由于作用单一矢量使得在控制周期结束时预测值和参考值间存在误差较大所致。文献[10-11]提出三矢量合成的方法,利用空间矢量脉宽调制SVPWM(space vector pulse width modulation)算法将3 个电压矢量组合来逼近控制周期结束时的参考值,以达到降低并网电流纹波的目的,同时实现固定开关频率控制;文献[12]通过引入虚拟矢量来增加预测控制中的候选矢量集,能有效减少参考电压和预测电压之间的误差,从而改善了网侧电流质量;文献[13]根据作用时间与目标函数值呈反比特性,通过选取扇区内目标函数最小的3 个矢量合成最优电压矢量,来降低电网电流THD。
针对以上问题,本文提出一种基于双矢量的无权重型模型预测控制UF-MPC(unweighted factor model predictive control),研究了基于Vienna 整流器的无权重因子预测控制策略实现直流侧中点波动抑制问题,同时结合零矢量实现双矢量固定开关频率控制。首先,通过电网电压极性进行扇区划分,同时预判直流母线上下电容的电压大小,优选出矢量个数为3 的矢量集,结合直接功率控制得到有功和无功功率的预测值,并设计单目标价值函数遍历找到最优矢量。然后,计算最优矢量和零矢量的占空比,来实现双矢量固定开关频率控制。最后,搭建基于RT-LAB 半实物平台,验证所提策略的可行性和有效性。
1 三相Vienna 整流器系统离散模型
图1 所示为三相三电平Vienna 整流器的电路拓扑示意。其中,ugx(x=a,b,c)为三相交流侧电网电压;igx为三相流经电感L 上的电流;Dxp~Dxn为二极管整流桥;Sx1和Sx2是由两个反向串联开关管构成的双向开关;C1、C2为2 个分裂电容;udc为直流输出电压;up和un分别是连接至中点o 的上、下电容电压。

图1 三相三电平Vienna 整流器的电路拓扑Fig.1 Circuit topology of three-phase three-level Vienna rectifier
根据基尔霍夫电压定律得到三相Vienna 整流器的数学模型,并进行Clark 变换,表达式为
式中:ugα和ugβ为通过Clark 变换的α 轴和β 轴电源电压;igα和igβ为通过Clark 变换的α 轴和β 轴网侧电流;uαo和uβo为通过Clark 变换的桥臂点对直流侧中点o 的α 轴和β 轴电压。根据瞬时功率理论,计算得到系统交流侧在两相αβ 静止坐标系下的瞬时有功功率p 和瞬时无功功率q,即
对式(2)两侧求导,得到网侧的有功功率和无功功率的变化率分别为
在电网电压理想的条件下Vienna 整流器网侧电压关系表示为
式中:Ug为相电压幅值;ω 为电网电压角频率。对式(4)两侧进行微分计算,同时结合式(4)可得到Vienna 整流器网侧电压在t 时刻的变化率,即
将式(1)和式(5)代入式(3)中,通过计算整理,可得t 时刻有功功率p 和无功功率q 的变化率为
假设控制系统的采样周期为Ts(取值为2×10-5s),且远远小于电网电压的周期。系统网侧有功功率和无功功率的预测值可通过一阶前向欧拉法来获取,即
式中:pp和qp为k 时刻的有功功率和无功功率;pp(k+1)和qp(k+1)分别为有功功率和无功功率的预测值。由于网侧电阻R 很小,因此将式(1)中的电阻项忽略掉,同时结合式(6)和式(7),可得整流器网侧输入有功和无功功率的预测值分别为
依据功率变化最小化标准来设计目标函数g(i),表示为
式中,p*和q*分别为有功功率和无功功率的参考值。为使整机工作在单位因数状态下,q*取值为0。对候选矢量集中的每个矢量放入目标函数中进行评判,以获得最小值对应的电压矢量,即最优矢量。
传统FCS-MPC 实现中点电位平衡时需要在目标函数中加入附加项,即
式中,up(k+1)和un(k+1)分别为直流侧上、下电容的电压预测值。
传统FCS-MPC 中不同权重因子选取对网侧电流THD 的影响如图2 所示。通过图2 可以看到,系统的最优控制依赖于权重因子λ 的合理取值,而λ的不同取值对中点电位和网侧电流THD 产生较大影响。由于λ 与控制变量间没有直接的数学关系,造成λ 的整定较为困难。故本文提出了无权重型预测控制来实现直流侧中点电位平衡。
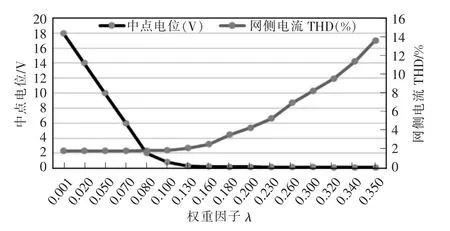
图2 传统FCS-MPC 中不同权重因子选取对网侧电流THD 的影响Fig.2 Influence of different weight factors on grid-side current THD in traditional FCS-MPC
2 无权重型模型预测控制方法
传统FCS-MPC 策略解决三电平整流器的中点电位不平衡问题时,通常采取在目标函数中增加含权重因子λ 的附加项来实现,由于系统运行在不同工况时权重因子选取较为困难。因此,利用冗余小矢量对中点电位的不同充放电特性来实现无权重因子型预测控制。
2.1 UF-MPC 无权重型中点平衡控制算法
直流侧中点电位波动过大时会增大功率器件和电容的电压应力,甚至网侧电流质量会急剧恶化,严重影响系统性能。因此,有必要对直流侧的中点电位波动大小进行抑制。本文采用基于冗余小矢量作用的矢量筛选策略,通过预判上、下电容电压的大小,同时结合电网电压极性,优选出的冗余小矢量可以达到平衡中点电位的目的。
根据电压矢量幅值大小的不同,三相Vienna整流器25 种开关状态可以分为大矢量、中矢量、小矢量和零矢量。由于前级二极管整流桥的特点,另外2 个电压矢量([PPP]、[NNN])不存在,电压矢量如图3 所示。以参考电压矢量落在扇区I(-30°~30°)内为例,分析该扇区内电压矢量对直流侧中点电位的作用效果。
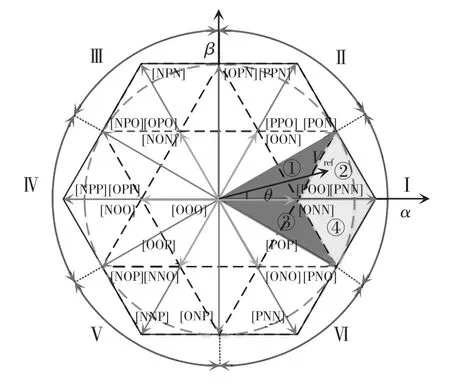
图3 三相Vienna 整流器的空间电压矢量Fig.3 Space voltage vector of three-phase Vienna rectifier
图4 为扇区I 内电压矢量的作用过程,对三相Vienna 整流器分析其工作原理可知,大矢量[PNN]和零矢量[OOO]不对中点电位产生偏移,中矢量([PON]、[PNO])和小矢量([POO]、[ONN])会对直流侧中点注入或流出电流,而中矢量对直流侧中电位的影响是不可控的。因此,利用冗余小矢量([POO]、[ONN])对直流侧上、下电容充放电的不同特点,来达到降低中点电位波动的目的。其中[POO]和[ONN]这对冗余小矢量对中点电位偏移有相反作用,小矢量[POO]是对上电容C1充电,使得C1两端的电位升高,而小矢量[ONN]是对下电容C2充电,使得C2两端的电位升高,可看到这对冗余小矢量对中点电位的影响呈相反状态,因此根据中点电位的正负偏差调整期望冗余小矢量的作用即可实现中点电位平衡控制。扇区I 有限控制集的选取原则如表1 所示,其他扇区的矢量集选取原则类似。
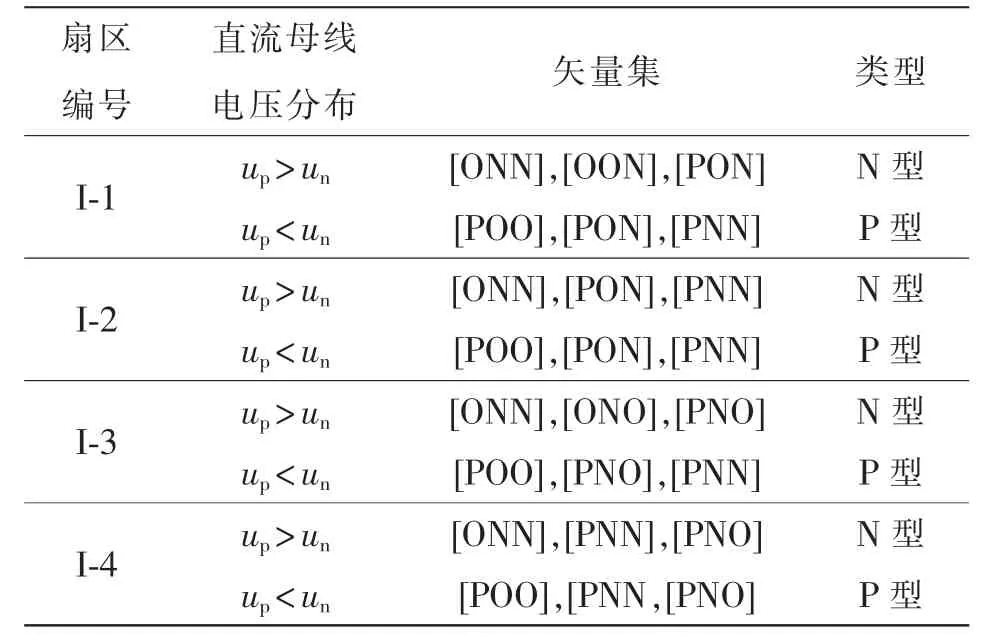
表1 矢量集的选取原则Tab.1 Selection principle for vector set
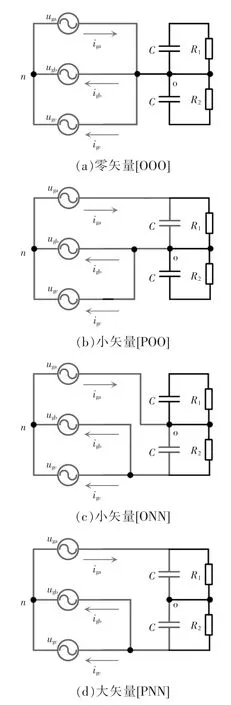
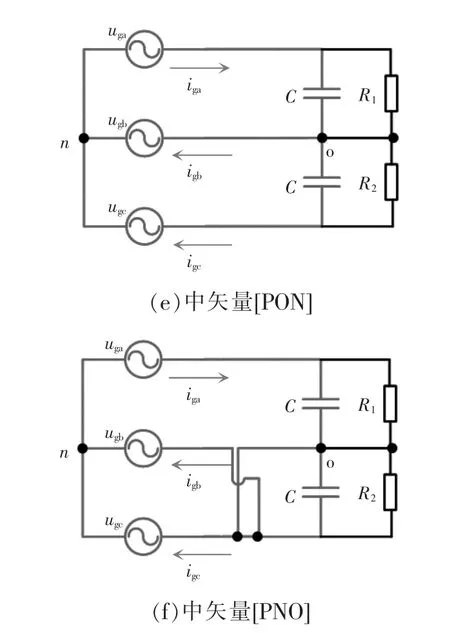
图4 扇区I 内电压矢量的作用过程Fig.4 Action process of voltage vector in Sector I
2.2 UF-MPC 固定开关频率策略
传统FCS-MPC 策略在一个控制周期中只作用单一电压矢量,这将造成网侧电流纹波较大。由于矢量选择的随机性,该策略也具有开关频率不固定的缺点。因此,本文引入矢量占空比的思想来实现开关频率固定的目标,在获取最优矢量的基础上结合零矢量实现了双矢量定频控制。首先,按照给定功率和反馈功率误差最小原则获得最优矢量,然后在一个控制周期中作用最优矢量和零矢量,其中最优矢量的作用时间根据功率误差最小的原理计算得到。
本文模型预测内环结合直接功率控制,利用价值函数滚动寻优获得最优矢量后,需要计算最优矢量和零矢量的作用时间。假设功率斜率在极其小的采样周期Ts内保持不变,则控制周期结束时的有功功率pk+1和无功功率qk+1可表示为
式中:pk和qk分别为第k 时刻的有功功率和无功功率的预测值;fpv和fpz分别为最优矢量和零矢量作用时有功功率的斜率;fqv和fqz分别为最优矢量和零矢量作用时无功功率的斜率;tv和tz分别为最优矢量和零矢量的作用时间。
结合第k 个采样周期瞬时功率变化率可以得到斜率fpv、fpz、fqv和fqz的表达式,即
根据式(11)和功率误差的概念,功率的预测值和参考值pref、qref之间的误差perror、qerror表示为
以最小功率误差平方和的形式定义目标函数G,并使目标函数最小化,即有
整理式(13)和式(14),可以求出最优矢量和零矢量的作用时间tv和tz分别为
由此可以得到在一个控制周期Ts内最优矢量和零矢量作用在时间刻度上的双矢量序列。通过驱动电路将双矢量对应的脉冲序列作用于开关管,从而达到固定开关频率的目标。同时,相较于仅单一矢量的作用,本文所提策略由于双矢量的作用,网侧电流纹波得到了降低。
3 实验验证分析
为验证所提UF-MPC 控制策略的正确性和有效性,本文搭建了基于RT-LAB 半实物平台。实验系统电路参数如表2 所示。

表2 系统的电路参数Tab.2 Circuit parameters of system
本文针对三相Vienna 整流器,采用基于双矢量的无权重型预测控制策略,其控制框图如图5所示。
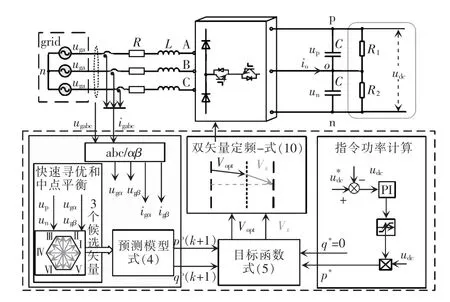
图5 基于双矢量的无权重型预测控制策略框图Fig.5 Block diagram of UF-MPC strategy based on double vectors
该策略采用双环控制,外环为直流侧PI 电压环,内环为结合直接功率的模型预测控制。其控制步骤如下:首先,根据电网电压极性可以分为6 大扇区(分别为Ⅰ~Ⅵ),每个大扇区又分成4 个小扇区;同时通过比较直流侧电压up和un的大小,优选出中点电位趋于平衡的冗余小矢量。然后,通过外环PI 控制得到内环有功功率的给定值p*,将无功功率参考值q*设为0,从而确定出当前时刻个数为3 的候选矢量集。最后,在此矢量集中,通过目标函数最小化获取最优矢量,并结合零矢量来达到固定开关频率的目标。本文所提策略的流程如图6 所示。
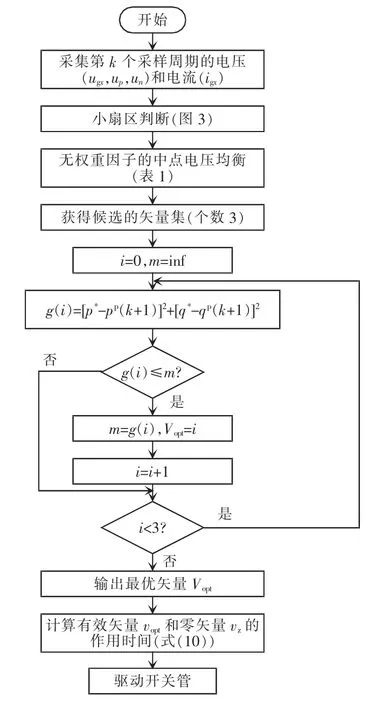
图6 基于双矢量的无权重型预测控制流程Fig.6 Flow chart of UF-MPC based on double vectors
图7 为系统由满载切换到半载时不同控制策略的暂态响应结果。在满载工况下,利用示波器测得传统FCS-MPC 和所提UF-MPC 策略下的网侧输出电流THD 分别为3.39%和2.28%,可看出本文所提控制策略降低了电网电流纹波,主要因为双矢量的作用使得控制周期结束时预测值和参考值的误差进一步降低,电流纹波更小。
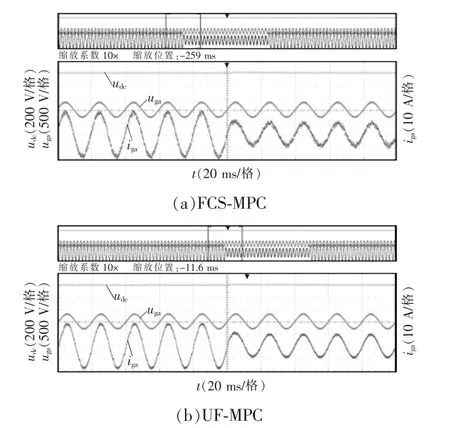
图7 不同控制策略的网侧电流暂态波形Fig.7 Transient waveforms of grid-side current under different control strategies
图8 给出了满载工况时2 种控制策略在直流侧上、下电容电压(up、un)和直流侧中点电位波动uo(uo=up-un)的波形。由图8(a)可见,采用传统FCSMPC 控制时,直流侧中点波动量uo为15.4 V,而所提UF-MPC 控制策略的中点波动量仅为3.6 V,说明采用无权重因子的控制策略平衡中点电位能力较强,同时避免了权重因子的选取困难问题,一定程度简化了控制策略的复杂度。
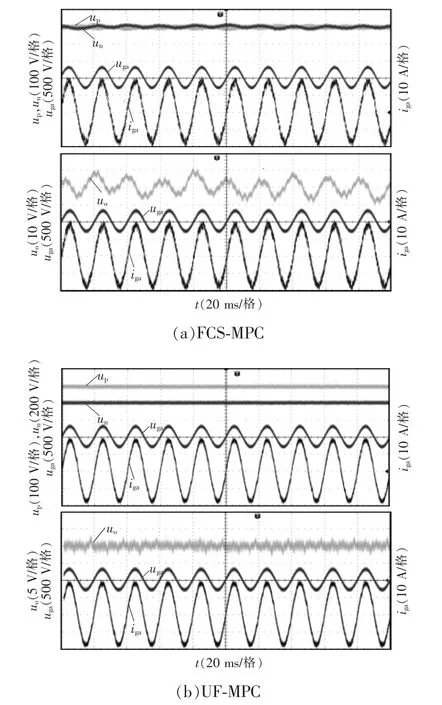
图8 不同控制策略的直流侧中点电位波动波形Fig.8 Waveforms of DC-side neutral-point potential fluctuation under different control strategies
4 结语
本文对模型预测控制应用在三电平变换器上的不足之处进行改进,以Vienna 整流器为研究对象,提出一种基于双矢量的无权重型预测控制策略,避免权重因子难以选取问题,并优选出冗余小矢量来实现无权重因子的中点电位平衡控制。通过RT-LAB 半实物测试平台对所提方案进行效果验证,实验结果表明,所提UF-MPC 控制和传统FCSMPC 策略相比,具有直流侧中点电位波动更小的优势;同时通过引入双矢量定频控制有效改善了电流的谐波。本文提出的控制策略不仅适应于Vienna整流器,对其他三电平变换器也同样适用。

