基于双主动全桥双向DC/DC 变换器的混合单移相调制方案
李 宇,张鑫蕊,税朝会,黄剑琪,龙 鹏,张津华
(1.贵州万峰电力股份有限公司,兴义 562400;2.国网湖北直流运检公司,宜昌 443000)
双主动全桥DAB(dual active bridge)双向DC/DC 变换器由于其具有如对称结构、双向潮流能力、宽软开关区域和灵活的控制能力等优点,被认为是隔离型双向DC-DC 变换器的核心拓扑[1]。同时,随着宽带隙半导体器件如GaN、SiC 等的出现和磁性材料的发展,DAB 变换器已广泛应用于电力电子变压器PET(power electronics transformer)[2-3]、电动汽车EV(electric vehicle)[4]和储能系统ESS(energy storage system)[5]等领域。因此,DAB 变换器有着广阔的应用场景。
控制DAB 变换器最简单的方法是单移相调制PSM(phase shift modulation)方案,其通过控制变换器原副边全桥之间的移相角来控制功率传输的方向和大小,这里定义这个移相角为外部移相角。然而在轻载条件下,当变换器的输入或输出电压变化较大时,会产生大量的无功功率,同时部分开关管的零电压开关ZVS(zero voltage switching)操作会丢失而直接导致转换效率变低[5]。为了克服PSM 方案的不足,很多学者开发了不同的优化调制方案,如扩展相移EPS(extended phase shift)调制方案[6-7]、双相移DPS(dual phase shift)调制方案[8]、三重相移TPS(triple phase shift)调制方案[9-16]等,其中EPS 调制方案和DPS 调制方案含有2 个控制变量,TPS 含有3 个控制变量。除了外部相移角,对于EPS 调制方案,2 个全桥中其中一个全桥内部还存在移相角;而DPS 调制方案,2 个全桥内部存在相等的移相角;在TPS 调制方案中,2 个全桥内部存在不相等的移相角。采用这些优化调制方案,DAB 变换器实现了较低的电流应力和较宽的软开关范围,从而提高了整体效率。然而,控制自由度的增加使得这些优化方案的实现变得更加复杂,要很好地应用在工程实际中还有很长的路要走。因此,为了提高变换器的效率,同时保留控制的简单性,有必要探索其他方案。
基于此,本文在文献[3]的基础上,提出一种混合PSM 方案。其主要思想是让EPS、DPS 以及TPS 调制方案中的所有控制变量相等,从而形成4 种不同的PSM 方案,即PSM-Ⅰ、PSM-Ⅱ、PSM-Ⅲ、PSM-Ⅳ方案。接着,比较这些调制方案的稳态特征,主要包括传输功率容量、均方根电流和软开关性能等。由于这些调制方案在不同的特性上表现出不同的稳态特征,所以为在整个负载范围内提出控制简单、更为合理有效的调制方案,对这些PSM 方案进行一定程度的混合,进而提出混合PSM 方案。
1 统一模型
DAB 转换器的拓扑结构如图1 所示,它由2 个全桥H1和H2、2 个直流电容C1和C2、一个电感器L和一个高频变压器T 组成。该变换器通过调制2 个全桥上的开关管S1~S8从而产生高频交流电压vab和vcd,然后叠加在电感器L 上进行能量的传输。其中,电容C1和C2用于滤波和稳定端口电压,变压器T 的主要作用是电气隔离和电压匹配,V1为原边侧输入电压,V2为副边侧输入电压,高频变压器匝数比定义为N∶1,fs为开关频率,Ts为开关周期,ω为开关角频率,电压增益定义为M=NV2/V1。
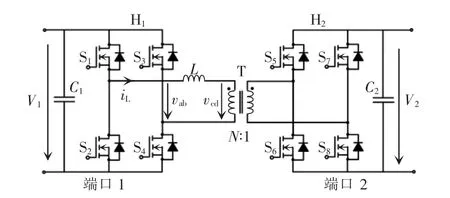
图1 DAB 变换器的拓扑结构Fig.1 Topology of DAB converter
DAB 转换器可以实现双向功率传输,当功率从端口1 传输到端口2 时,定义为正向模式;当电源从端口2 传输到端口1 时,定义为反向模式;由于这2 种模式分析方法类似,本文只讨论正向模式。在分析之前,这里对DAB 变换器进行了理想化,主要包括以下3 点:①变换器工作在稳定状态;②所有开关都是理想的;③变压器是具有无限磁化电感的理想变压器。
TPS 调制方案作为目前最广义的调制方案,其典型的波形如图2 所示。在图2 中展示了变换器原副边开关管的开关时序、原副边的电压波形等。TPS调制方案下,所有开关管都是以50%的占空比开通和关断,且不同桥臂之间开关管的开通时序不同,从而形成了不同的控制变量。例如:在原边侧全桥H1中,超前桥臂中开关S1和滞后桥臂中的开关管S4之间的移相形成了变量D1Ts;副边侧全桥H2中,开关管S5和开关管S8之间的移相形成了变量D2Ts;变换器原副边电压波形高电平的中心之间的移相形成了变量D0Ts,这些变量的大小共同决定了传输功率的大小,同时形成了不同的稳态特征。所以探究这些变量如何影响传输功率和稳态特征非常有必要。对变换器建模分析是理解和量化控制变量与稳态特征之间关系的一种很好的方式,下面通过建模具体分析。
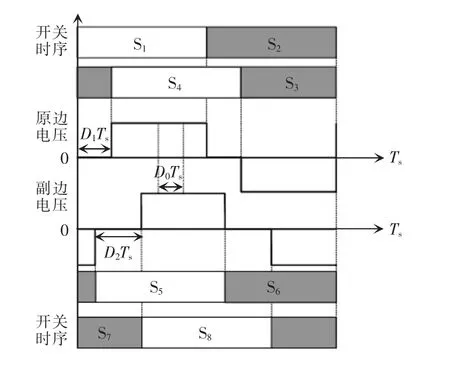
图2 TPS 调制方案下的典型波形Fig.2 Typical waveform under TPS modulation scheme
由于可调控变量比较多,该调制方案的系统模型随着时间段及工作状态的不同会变得相对复杂。所以,为了建立比较简单通用的模型,采用时域分析方法对其稳态建模不再合适。为了得到更加简单的模型,本文基于傅里叶级数展开建立了一个开关周期内的统一模型[9]。首先,以开关管S1导通时刻之前的D1Ts/2 为零时刻点,DAB 变换器中变压器的原、副边侧电压可以通过傅里叶级数分解得到,即
考虑到DAB 变换器的电流在一个开关周期内的对称性,同时依据式(1)可以得到电感的表达式为
进一步,可以得到电感电流有效值ILrms的表达式为
则DAB 变换器在一个开关周期内的平均功率为
这样就对TPS 调制方案下DAB 变换器的统一模型求解完整了,其具体的求解过程可以参考文献[9]。从式(1)~式(5)可以看出,通过基波分量和各个高次谐波分量可以对电压、电流以及传输功率等稳态特征进行统一表示。如前所示,PSM、EPS以及DPS 调制方案都是TPS 调制方案的特殊形式,例如当D1=D2=0 时,TPS 调制方案就是PSM 调制方案;当D1=0 或者D2=0 时,TPS 调制方案就是EPS 调制方案;当D1=D2时,TPS 调制方案就是DPS调制方案。为了保持PSM 调制方案的简单性,在EPS、DPS 以及TPS 中,让各个控制变量相等就可以得到不同的PSM 方案。
(1)当D1=D2=0 时,控制变量为D0,这种调制方案就是传统的PSM 调制方案,本文将其定义为PSM-Ⅰ;
(2)当D2=0 时,控制变量为D1=D0,这种调制方案定义为PSM-Ⅱ;
(3)当D1=0 时,控制变量为D2=D0,这种调制方案定义为PSM-Ⅲ;
(4)当控制变量为D1=D2=D0时,这种调制方案定义为PSM-Ⅳ。
很显然,前面求解的统一模型适合这4 种PSM 方案。由于PSM 只要一个控制变量,不存在优化概念,所以通过频域分析对其建立统一的模型即可。本文依据上述统一模型对这几种PSM 方案从传输功率容量、均方根电流和软开关性能等方面展开讨论。
2 稳态特征的比较
本节主要对不同PSM 调制方案的一些稳态特征进行比较,主要包括传输功率容量、均方根电流和软开关性能等方面。
2.1 传输功率容量
传输功率容量是变换器最基本的一个特征,其大小直接决定了变换器是否适应某个应用场景。首先选择传输功率的基准值为PN=kV1V2/(4πLω),对传输功率进行标幺化,可以得到
把不同PSM 调制方案的约束条件代入式(6)中,可以得到不同PSM 调制方案的传输功率容量,如图3 所示。
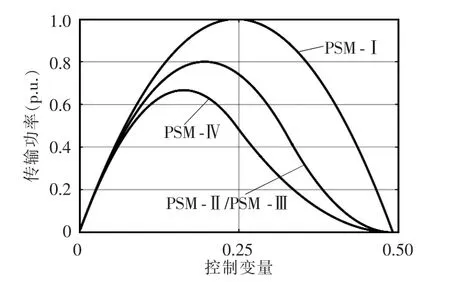
图3 不同PSM 调制方案传输容量的比较Fig.3 Comparison of transmission capacity among different PSM modulation schemes
从图3 可以看出,PSM-Ⅰ方案具有最大的传输能力,传输功率标幺值的最大值达到1,并且传输范围相对于0.25 是对称的。PSM-Ⅱ方案和PSM-Ⅲ方案的传输容量为PSM-Ⅰ调制方案的0.8 左右,而PSM-Ⅳ方案的传输容量最小。
2.2 电感电流有效值
DAB 变换器的损耗主要包括半导体器件的开关损耗和导通损耗、磁性元件的导通损耗和铁芯损耗。为了探讨这些调制方案在导通损耗之间的差异,可以比较和导通损耗成正比的电感电流有效值。为了考察开关损耗之间的差异,可以比较不同调制方案之间实现零电压开通的情况。对于铁芯损耗,当电压确定后,本文就假定该损耗不再改变。另外,为了更加详细地进行比较,表1 给出了DAB 变换器的主要技术参数。

表1 DAB 变换器的技术参数Tab.1 Technical parameters of DAB converter
依据变换器传输功率的表达式,4 种PSM 方案在V2=95 V 时能够传输的功率分别为859、687、687、573 W;而当4 种PSM 方案在V2=152 V 时能够传输的功率分别为1 375、1 100、1 100、916 W。由于变换器设定功率的最大传输功率为850 W,很明显如果单纯只采用PSM-Ⅱ、PSM-Ⅲ以及PSM-Ⅳ方案是无法满足功能要求的。
下面对电感电流有效值进行比较,图4 给出了DAB 变换器在M=0.5 和M=0.8 时的电感电流RMS比较情况,也就是输入V1=380 V,输出电压分别对应V2=95 V 和V2=152 V。图4(a)为M=0.5 的情况,从图4(a)中可以看出PSM-Ⅱ方案得到的电感电流有效值最小,其次是PSM-Ⅳ和PSM-Ⅰ方案,当传输功率越来越大时,PSM-Ⅳ方案的表现没有PSM-Ⅰ方案好。相比较之下,最差的就是PSM-Ⅲ方案,在整个负载范围内其得到的电感电流有效值基本都是最大的。图4(b)为M=0.8 的情况,4 种调制方案得到的电流水平基本差不太多,尤其是在轻载的情况下。但整体而言,其规律和M=0.5 类似,依旧是PSM-Ⅱ方案得到的电感电流有效值保持最小。从而得出的结论:随着M 越偏离1,PSM-Ⅱ方案的优势越明显,其次是PSM-Ⅰ方案。
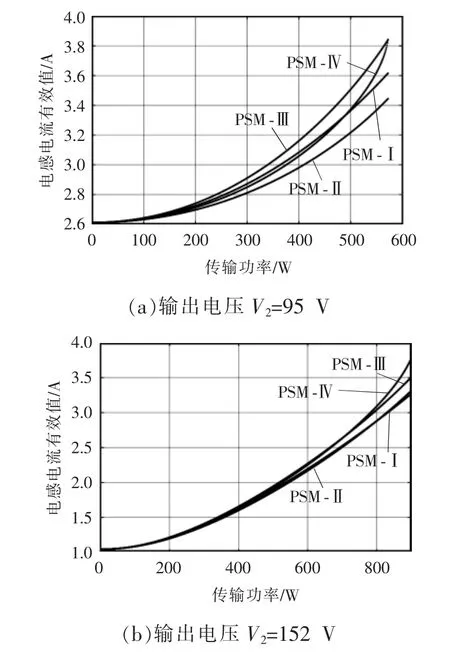
图4 不同PSM 调制方案电感电流有效值的比较Fig.4 Comparison of inductor RMS current among different PSM modulation schemes
2.3 软开关范围
实现零电压开通以减少开关损耗,特别是对于MOSFET 开关管而言至关重要。要想实现零电压开通的基本条件有2 个:①必要条件,在开关导通之前,电感器电流需要流经开关的体二极管,也就是电流的方向需要得到满足;②充分条件,存储在电感器中的能量应大于变换器桥臂上下开关寄生电容中存储的总能量。为了简化分析,本文只用必要条件来评价不同PSM 方案实现软开关的范围。将表1 的技术参数代入式(2)得到的电感电流表达式进行多次叠加,可以得到不同开关管实现软开关的情况,如图5 所示。
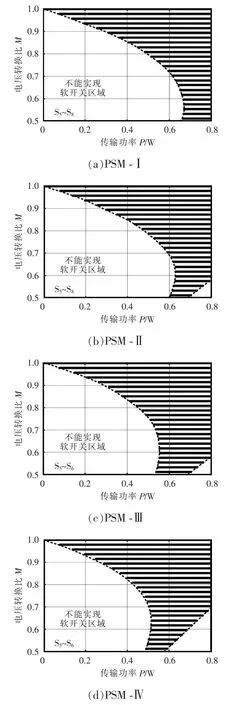
图5 不同PSM 调制方案软开关范围的比较Fig.5 Comparison of soft switching range among different PSM modulation schemes
图5 中阴影区域表示开关管实现了软开关,而其他区域表示开关管要么无法实现零电压开通,要么不具备传输功率的能力,其具体情况已经在图5中进行了标注。无论是哪种PSM 方案,它们的原边侧开关管都能够很好地实现软开关,所以重点比较副边侧开关管的情况。图5(a)表示PSM-Ⅰ方案开关管S5~S8实现软开关的情况,图5(b)表示PSM-Ⅱ方案开关管S5~S8实现软开关的情况,可以看出PSM-Ⅰ方案实现软开关范围比PSM-Ⅰ方案稍微宽一点。图5(c)表示PSM-Ⅲ方案开关管S5、S6实现软开关的情况,而开关管S7、S8在整个负载范围内都不能够实现软开关。图5(d)表示PSM-IV 方案开关管S5、S6实现软开关的情况,而开关管S7、S8在整个负载范围内同样都不能实现软开关。从图5 中可以看出,在PSM-Ⅱ和PSM-Ⅳ方案下,虽然开关管S5、S6实现软开关范围要比PSM-Ⅱ和PSM-Ⅰ方案宽,但由于开关管S7、S8在整个负载范围内都不能够实现软开关。所以,相比较而言,PSM-Ⅱ方案在整个负载范围内的软开关范围最宽。
2.4 混合PSM 方案
通过以上比较分析可知,从传输功率的角度,PSM-Ⅰ方案的范围最宽,其次是PSM-Ⅱ和PSM-Ⅲ方案;从电感电流有效值的角度,PSM-Ⅱ在整个负载范围内表现最小,其次是PSM-I 方案;从软开关范围的角度,PSM-Ⅱ方案实现零电压开通的开关管范围更广,其次是PSM-Ⅰ方案。所以基于此,为了提高变换器的变换效率,本文提出了混合PSM方案,具体为低功率段为PSM-Ⅱ方案,高功率段为PSM-Ⅰ方案,这样得到的调制方案就可以覆盖整个功率范围。值得注意的是,高低功率的分解段为PSM-Ⅱ方案能够传输的最大传输范围。综上,所提出的混合PSM 方案相比传统PSM 方案而言,减小了电感电流有效值,拓展了实现软开关的范围,从而提高了变换器的效率。与目前比较典型的优化调制策略相比,本文所提调制策略仅仅只有一个调制变量,实现起来更加简单,可以更好地应用在工业领域中。
3 实验验证
为了验证2.4 节提出的混合PSM 方案,本文搭建了DAB 变换器的实验样机。实验样机的相关技术参数如表1 所示。另外,磁芯材料的设计采用了PC90 的材质,这样可以使得变换器工作在更大的磁通密度下,不容易饱和。其样机如图6 所示。

图6 实验样机Fig.6 Experimental prototype
图7 给出了DAB 变换器在V2=95 V 时混合调制方案的稳态波形。在该情况下,混合调制方案中从PSM-Ⅱ方案切换到PSM-Ⅰ方案的功率点为P=687 W。
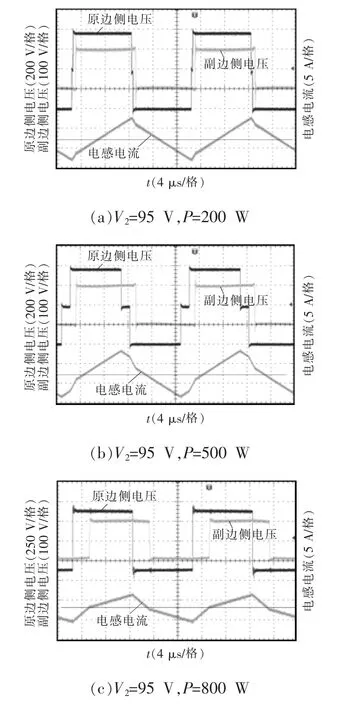
图7 混合PSM 调制方案在不同功率下的波形Fig.7 Waveforms under hybrid PSM modulation scheme at different powers
图7(a)为P=200 W 时变换器的稳态波形,从图中可以看出,该调制方案为PSM-Ⅱ方案,变压器原边侧的波形为三电平波形,副边侧为方波,其原边侧零电平的电平宽度和外部移相角相等。图7(b)为P=500 W 时变换器的情况,可以看出混合调制在该情况下也为PSM-Ⅱ方案。结合图7(a)和(b)可以看出,随着传输功率的增大,控制变量也增大。图7(c)为P=800 W 时变换器的稳态波形,可以看出混合调制在该情况下为PSM-Ⅰ方案,变压器原副边的波形都为方波,它们之间存在移相角来调节传输功率的大小和方向。通过以上结果验证了混合PSM 方案的可行性。
图8 给出了DAB 变换器在V2=95 V、P=400 W时不同调制方案下的稳态波形。首先,通过测试PSM-Ⅰ、PSM-Ⅱ、PSM-Ⅲ、PSM-Ⅳ调制方案的电感电流有效值分别为3.12、3.01、3.18 和3.08 A,而对应其理论值为3.08、2.98、3.16 和3.05 A,可以发现测试结果基本和理论保持一致。另外,从图8 中可以看出,4 种PSM 方案中变换器原边侧都可以实现零电压开通,而副边侧的波形由于电感电流方向不满足,开关管都不能够实现零电压开通。
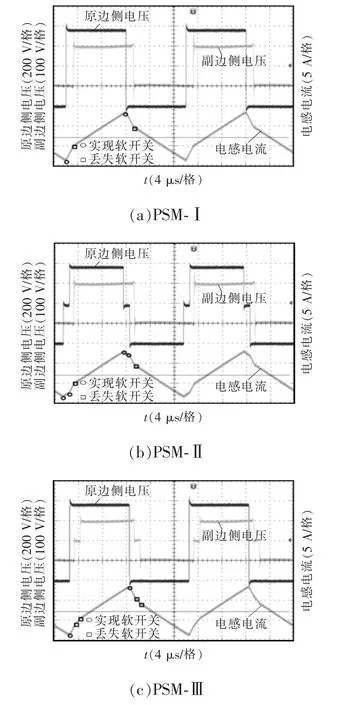
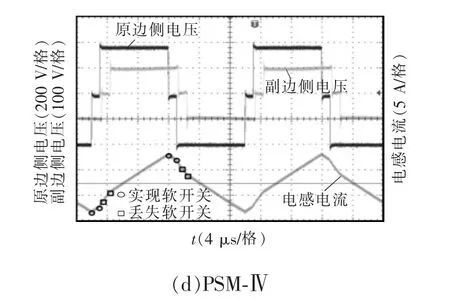
图8 不同调制方案的比较Fig.8 Comparison among different modulation schemes
最后,图9 给出了混合PSM 方案和各个不同PSM 方案效率的对比。图9(a)为V2=95 V 时各个调制方案效率的对比,从图中可以看出,在0~687 W 时混合PSM 方案采用的是PSM-Ⅱ方案,在687~859 W时变换器采用的是PSM-Ⅰ方案,而整个负载范围内混合PSM 调制方案的效率最高。图9(b)给出了V2=152 V 时各个调制方案效率的对比,从图中可以看出,整个负载范围内都采用PSM-Ⅱ方案,而且其效率表现最好。综上所述,本文所提出的混合PSM 方案,提高了变换器的效率,同时还保留了控制的简单性,可以更好地应用在工程实际中。
4 结语
本文提出了一种混合单移相调制方案,在不增加控制复杂程度的基础上,减小了电感电流有效值,扩大了实现软开关的范围,从而提高了变换器的效率。首先,在EPS、DPS 以及TPS 调制方案的基础上让各个控制变量相等,从而形成了不同的PSM方案。接着,利用TPS 调制方案的统一模型对这些PSM 方案从传输功率容量、电感电流有效值以及软开关范围等不同角度进行了比较,结果为PSM-Ⅰ方案的传输功率容量最大,而PSM-Ⅱ方案的软开关范围更宽,电感电流有效值更小。基于此,本文把PSM-Ⅰ方案和PSM-Ⅱ方案进行了结合,形成了一种新的混合单移相调制方案,使得整个负载范围内变换器的稳态特性更加优秀。最后通过实验验证了混合PSM 方案的优越性。

