金属化膜电容元件宽频特性研究

易承乾，李超然，张波，贾华，盖斌，黄葵，邓光昭，吴云翼，李婉

（1.清华大学电机工程与应用电子技术系，北京 100084；2.西安高压电器研究院股份有限公司，西安 710077；3.嘉善赛晶电容有限公司，浙江 嘉善 314100；4. 中国长江三峡集团有限公司科学技术研究院，北京 101199）

0 引言

作为高压直流输电工程的“心脏”，换流阀长期受到学者和业界的关注。大容量金属化膜电容器由于具有重量轻、结构紧凑、可自愈等优点[1-2]，被广泛使用在换流阀中[3-4]。作为换流阀中最重要的组成部件之一，电容器故障率在整个换流阀中仅次于电力电子开关[5]。因此，金属化膜电容器的稳定性直接影响到整个换流阀乃至电力系统的稳定性，需要重点关注[6-7]。

在换流阀中，电力电子开关的动作快速且频繁。以模块化多电平换流器（modular multi-level converter，MMC）为例，大容量金属化膜电容器在换流阀中起到支撑电压和平衡瞬时功率的作用。在开关动作的瞬间，电容器上的电流在0 和数百安培之间迅速变化，此切换过程往往在数微秒内完成[8-9]。导致电容器在开关切换的过程中将承受快速变化电流（即高频电流）的冲击[10]。因此，需要关注电容器在宽频范围的特性。

当前，研究人员主要使用数字电桥等设备来测量电容器在不同频率下的阻抗特性[11-12]。但是此方法仅能获得电容器的整体特性，无法对电容器内部的物理过程进行分析。有学者对低电压小容量电容器采用数据拟合的方法，建立了集总宽频等效电路描述电容器内部参数[13]。但由于研究的电容器较小，在其研究的频率范围内，内部电流等物理量分布均匀且保持不变，因此参数恒定的等效电路模型无法反映更普遍的情况。有学者简化电容器结构，使用解析求解或建立分布式等效电路的方法，研究了电容器在高频下的电流分布，发现在高频下电容器内部电流分布不均[14-17]。然而此类方法的建模和求解比较复杂，且需要对电容器进行较多的简化和假设。

本文以实际应用于换流阀的直流支撑电容器中的单个电容元件为研究对象，使用数字电桥对其在20 Hz~2 MHz 范围内的阻抗特性进行了测量，获得了宽频范围内电阻和电抗的变化规律。通过数据拟合的方法，建立了低频范围内参数恒定的等效电路模型。结合实测的高频下的薄膜参数，获得了高频范围电容器内部等效串联电感和电阻参数随频率变化的规律。

1 测量回路与方法

本文的实验对象为实际换流阀用大容量金属化膜电容器中的一个电容元件，其内部结构如图1所示。蒸镀完金属层的双向拉伸聚丙烯被卷绕在一根绝缘轴上，两个端面喷有金属用于电气连接[18]。为保证其高电压耐受能力，本文所使用的电容元件内部为串联结构。电容元件的高度为10 cm，绝缘轴直径为9 mm，整个元件的直径为76 mm。

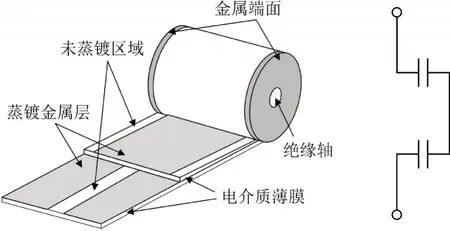
图1 电容器元件内部结构示意图Fig.1 Internal structural schematic diagram of capacitor element

本文使用数字电桥（Agilent，E4980A）对电容元件的阻抗特性进行测量，测量范围为20 Hz~2 MHz。通过按电容器尺寸固定测量回路、开路/短路校准等手段，消除高频测量过程测量回路带来的误差；将测量回路放入带屏蔽的烘箱内消除外界环境的干扰。

2 实验结果分析

2.1 阻抗特性

电容元件的阻抗可表示为Z=R+jX。阻抗大小与相位随频率变化的情况如图2所示。由图2 可知电容元件在150 kHz 左右发生谐振。在频率低于150 kHz 时，电容起主要作用，元件呈现容性，且随频率增加，阻抗值越来越小；当频率超过150 kHz 时，电感起主要作用，元件呈现感性，且随频率增加，阻抗值越来越大。

图2 电容元件阻抗特性Fig.2 Impedance characteristics of capacitor element

电阻R和电抗大小|X| 随频率变化的情况如图3 和图4 所示。在低频率范围，随频率增加，电阻逐渐减小并保持稳定，电抗逐渐减小，直至发生谐振；当频率高于谐振频率时，电阻R和电抗大小|X|均随频率增加而增加。在频率大于400 kHz 时电阻存在突然下降再缓慢增加的趋势，这可能是由内部结构导致的二次谐振[11]。

图3 电阻R 随频率变化趋势Fig.3 Variation trend of resistance R with frequency

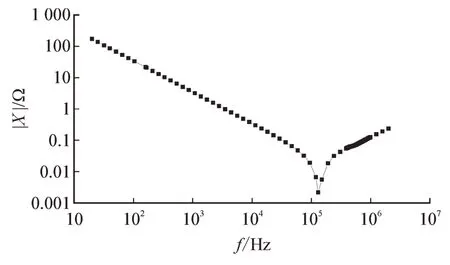
图4 电抗|X|随频率变化趋势Fig.4 Variation trend of reactance|X|with frequency

2.2 低频段

由电容元件内部电流路径分析可知：电流通过引线和端部金属端面流入，然后经过蒸镀金属层穿过聚丙烯薄膜，最后经蒸镀金属层和金属端面流出电容元件。因此可将电容元件等效为如图5 所示的等效电路图[13]。其中：R1表示接触电阻和金属部分的电阻；L表示由引线和卷绕结构等引起的电感；R4表示由趋肤效应导致的电阻；C1代表电容薄膜中的无损极化；R2是代表电容薄膜泄露电流的电阻；C2表示有损极化；R3表示极化损耗。

图5 电容元件等效电路图Fig.5 Equivalent circuit diagram of capacitor element

基于此等效电路模型可得到整个电容元件电阻R和电抗X的表达式为

式中，ω为角频率。

本文采用数据拟合的方法，对测量得到的电容元件阻抗数据进行拟合。在150 kHz 以下，拟合结果的拟合优度R2=0.999 1。拟合得到的等效电路中各参数的值如表1 所示。由表1 中结果可知，电容元件中无损极化占主导（C1>C2），电感大约在28.61 nH，聚丙烯薄膜的绝缘能力很好（R2）。

表1 拟合得到的等效电路中各参数值Table 1 Each parameter in the equivalent circuit obtained by the fitting

测量的电阻和电抗数据以及拟合的曲线如图6和图7 所示。由曲线和测量数据可看出，当频率低于150 kHz 时，使用表1 中的参数值和图5 所示的电路拓扑，可对电容元件进行较好的描述。但是，当频率超过150 kHz 时，使用拟合曲线得到的值与测量值有较大偏差。这是因为在高频下电容元件内部电磁耦合作用强烈，内部的电流分布将发生变化[14]，基于低频下的结果得到的等效电路拓扑和拟合的参数值将不再适用。

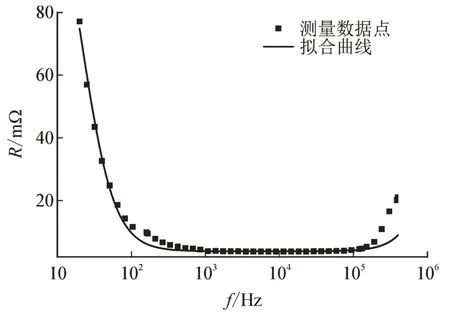
图6 电阻数据的拟合结果Fig.6 Fitting results for resistance data

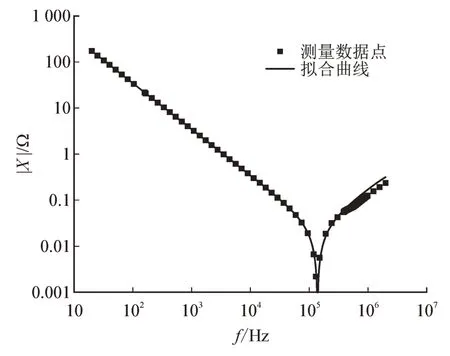
图7 电抗数据的拟合结果Fig.7 Fitting results for reactance data

2.3 高频段

电容元件中的电阻、电感和电容均会受到频率的影响。电容值主要受聚丙烯薄膜材料本身介电常数的影响。使用宽频介电谱仪测量纯聚丙烯薄膜宽频范围的相对介电常数εr和介质损耗角正切tanδ，结果如图8 所示。由图8 中结果可知：随着频率的增加，聚丙烯薄膜的相对介电常数略微减小，而介质损耗角增大。

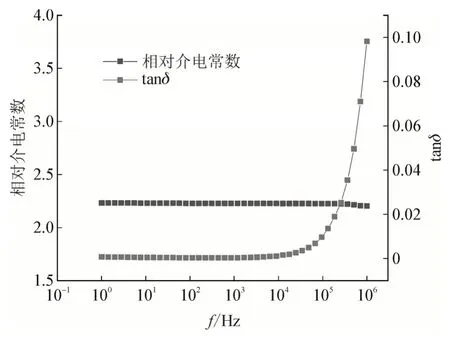
图8 宽频范围聚丙烯薄膜的相对介电常数与损耗变化情况Fig.8 Variation of relative dielectric constant and loss in polypropylene films over a wide frequency range

由于电容薄膜部分的参数可通过仪器测量得到，因此可将电容薄膜部分简化等效为电容Ce和电阻RC串联表示，如图9 中所示。各频率下具体的电容值和电阻值通过测量数据转化得到。

图9 简化的等效电路模型Fig.9 Simplified equivalent circuit model

在已知简化等效电路模型内部R1、Ce和RC的条件下，结合测量得到的阻抗数据，可通过求解方程（3）和方程（4）得到各频率下L和R4公式为

高频下L和R4随频率变化的结果如图10 所示。由图10 中结果可知：在高频下，电阻和电感参数不再保持恒定。随着频率的增加，表征趋肤效应的电阻R4总体先减小后增加，电容元件内部电流分布发生明显变化，出现类似趋肤效应的现象，导致电感值L减小。在频率大于400 kHz 时，R4值有一个先减小后迅速增大的趋势，这与电容器内部具体的电流分布有关。

图10 高频下等效电感L和电阻R4的变化情况Fig.10 Variation of equivalent inductance L and resistance R4 at high frequencies

3 结语

本文研究了单个电容元件在20 Hz~2 MHz 范围内的特性，得出如下结论：

1）电容元件在150 kHz 左右发生谐振。在低频率范围：随频率增加，电阻逐渐减小并保持稳定，电抗绝对值逐渐减小，直至发生谐振；在高频范围：电阻和电抗均随频率增加而增加。在频率大于400 kHz时电阻存在突然下降再缓慢增加的趋势，这可能是由内部二次谐振导致的结果；

2）在低频范围（<150 kHz），通过对测量数据进行拟合，建立了参数恒定的宽频等效电路模型；该模型可准确地描述电容元件在低频下的特性和内部物理过程；

3）在高频范围（>150 kHz），参数将发生频变。结合宽频范围聚丙烯薄膜介电常数和损耗的测量结果、电容元件的阻抗特性数据，求解发现随着频率的增加，电感值逐渐减小。表明电容元件会出现类似趋肤效应的现象，内部电流分布发生变化。

基于本文研究得到的高频下电感和电阻的结果，可尝试反演得到内部具体的电流分布，这是后续研究的目标。