弹性约束下变厚度蜂窝夹层板的隔声特性
王朝能,李凤莲,吕梅
(北京信息科技大学 机电工程学院,北京 100192)
0 引言
蜂窝结构起源于仿生学,蜂窝夹层复合材料具备复合材料的特点,并且其蜂窝材料及其特殊结构形式,扩宽了其应用范围。蜂窝夹层板结构具有轻质、优良比刚度/比强度、抗冲击性能以及隔热和隔音性能,在医疗设备、传感器、防护设备、航空航海及国防工程等领域有广泛的应用前景[1]。由于蜂窝结构有较高的减重率,现在的航天飞机、人造卫星、高铁、汽车等在内部大量采用蜂窝结构。由于蜂窝夹层板所运用的工况环境使其经常面临振动载荷和声压载荷激励,故有必要深入研究其振动和隔声特性。
近年来,大量学者对蜂窝夹层板结构进行了深入研究。Gibson等[2]首次提出了二维内凹六边形蜂窝结构,其结构具有负泊松比效应。研究夹层板结构振动主要有Reissner理论、Hoff理论和普鲁卡克夫-杜庆华理论。Hu等[3]分析了经典层合板理论(classical laminate theory,CLT)、一阶剪切变形理论(first-order shear deformation theory,FSDT)和高阶剪切理论在夹层复合材料研究中的适用性和效率。Li等[4]基于双曲切线剪切变形理论,利用Navier法和流固边界条件研究了2种不同类型的负泊松比功能梯度蜂窝夹层板的自由振动和隔声性能。Oliazadeh等[5]建立了基于统计能量分析(statistical energy analysis,SEA)的蜂窝夹层板分析模型,利用SEA方法对蜂窝夹层板的声透射损失进行了理论有效性验证,并给出了声透射损失的表达式。任树伟等[6]基于Reissner理论建立了简支边界下蜂窝夹芯板传声理论模型,通过与有限元分析结果对比验证了声学理论模型的正确性。周俊杰等[7]利用代表体元(representative volume element,RVE)法对蜂窝模型进行有限元等效建模,总结出了可靠的蜂窝夹层板的有限元等效模型。Shi等[8]采用瑞利-里兹法(Rayleigh-Ritz method)根据结构-声耦合系统的能量表达式对带声腔的双层板结构的振动声特性进行了分析研究,验证了理论的可靠性。
利用一阶剪切变形理论,结合改进的瑞利-里兹法[9-10],建立并求解了声振理论模型。通过有限元分析验证了理论的准确性。在此基础上,讨论了参数变化对变厚度蜂窝夹层板隔声性能的影响。采用的方法可以快速计算不同边界条件下蜂窝夹层板的振动及隔声特性。
1 理论模型的建立
负泊松比的变厚度蜂窝夹层板模型如图1所示,它由等壁厚的六边形蜂窝核心层和上下面板组成。在直角坐标系xyz中,x-y平面位于中间层蜂窝芯的中间平面上。板的长度和宽度分别为a和b,蜂窝芯层厚度为hc,板的最大厚度为hmax,相关厚度变化函数规律如下:
(1)

图1 变厚度蜂窝夹层板模型Fig.1 Honeycomb sandwich model with variable thickness
式中:ξ1、ξ2分别为沿x和y轴方向的厚度变化系数;hmin为板的最小厚度,可由hmax、ξ1、ξ2求解得到。
蜂窝芯的单元胞如图2所示。蜂窝的倾斜壁长为l1,蜂窝的上下壁长为l2,壁厚为tc,蜂窝的特征凹角为θ。随着特征角的变化,蜂窝芯的形态也发生变化。当θ>0°时,芯层为负泊松比凹六边形蜂窝,如图2(a)所示;当θ=0°和θ<0°时,负泊松比的凹六边形蜂窝将分别演化为图2(b)所示的零泊松比的准方形蜂窝和图2(c)所示的正泊松比的凸六边形蜂窝[11]。

图2 等壁厚蜂窝的单元胞模型Fig.2 Unit-cell models of the honeycomb with equal wall thickness
六边形蜂窝夹层板的面内等效弹性参数的研究已被广泛开展[12]。基于Gibson和Ashby提出的蜂窝等效理论及后来的修正蜂窝等效理论[13],给出了等壁厚负泊松比六边形蜂窝夹层板等效弹性参数的计算公式:
(2)
式中:Ex、Ey、Ez为x、y、z方向上的等效弹性模量;Gxy、Gxz、Gyz为等效剪切模量;νxy、νyx为等效泊松比;ρ为等效质量密度;蜂窝结构关系η1=l2/l1、η3=tc/l1;Es为材料杨氏模量;Gs=Es/[2(1+vs)]为材料弯曲模量,vs为材料泊松比;ρs为材料密度。
基于一阶剪切变形理论,蜂窝板位移场表示为
(3)
式中:u、v、w分别为变厚度负蜂窝夹层板中性面上任意一点的位移;φx、φy分别为夹层板的法线沿x和y轴的转角。
根据线性变形假设,其位移-应变关系表示为
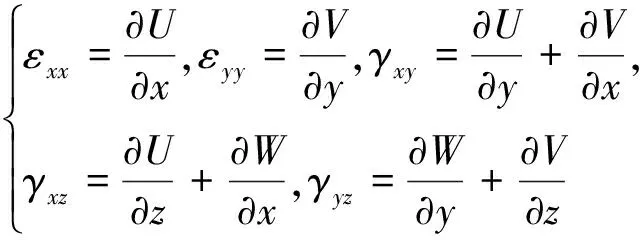
(4)
式中:εxx、εyy、γxy、γxz和γyz为应变分量。
根据广义胡克定律并且考虑负泊松比的蜂窝夹层板结构的正交各向异性,并结合式(2),其本构方程表示为
(5)

(6)
利用Hamilton原理,可以推导出负泊松比蜂窝夹层板的动力学方程为
(7)
式中:qz为分布在z上的外力;Nx、Ny和Nxy为应力的合力;Mx、My和Mxy为力矩;I0、I1和I2为广义惯性项;Qx和Qy为横向剪力的合力。这些变量可以表示如下:
(8)
通过改进的双傅立叶余弦级数和辅助多项式函数组合为位移场容许函数,多项式函数表示如下:
(9)
不考虑边界条件,蜂窝夹层板的每个位移和旋转分量展开为修正傅里叶级数为
(10)

(11)
对于变厚度蜂窝夹层板,应变能Us定义为
(12)
蜂窝板的动能T表示为
(13)
假设外力做的功We为
(14)
蜂窝夹层板结构的边界约束弹簧中的弹性边界能Usp表达式为
(15)
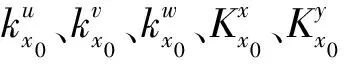
(16)
蜂窝夹层板的拉格朗日能量函数可以表示为
L=T-Us-Usp+We
(17)
通过拉格朗日能量函数并结合Rayleigh-Ritz法,可得到系统自由振动的矩阵方程:
(K-ω2M)G=0
(18)
式中:ω为入射声波的圆频率;Κ和M分别为板的刚度矩阵和质量矩阵,它们都是对称矩阵,可以写成:
(19)
(20)
式中:Kuu和Muu等均为子矩阵,其维度与截断数M和N有关,例如Kuu为方程组对x方向的位移函数,即式(10)中u(x,y)函数所包含的未知系数进行二次偏导后对应的项,其他子矩阵包括质量矩阵求解类似。
特征向量G为未知展开式系数,可表示为
G=[Gu,Gv,Gw,Gφx,Gφy]T
(21)
当平面简谐声波P以一定的入射角入射到蜂窝夹层板的上面板,如图1所示,其中入射方向矢量与z轴夹角为ψ1,入射方向矢量在x-y平面的投影与y轴夹角为ψ2。入射声压激励pi可表示为
pi(x,y,t)=p0ei (ωt-kxx-kyy-kzz)
(22)
式中:p0为入射声压幅值;kx、ky、kz分别为波数在x、y、z方向上的分量,其表示为
(23)
式中:k0=ω/c0,c0为声速。
考虑弹性边界条件下蜂窝夹层板的声振特性,反射声压pr和透射声压pt可以表示为
(24)
式中:wmn为式(10)中w(x,y)函数;Rmn和Tmn分别为反射声压幅值和透射声压幅值。
蜂窝夹层板系统在入射声压、反射声压和透射声压激励下的外力可以表示为

(25)
在蜂窝夹层板顶板、底板与空气交界处,需满足流固耦合条件,即法向速度分量相等,表示为

(26)
根据以上理论条件,将动力学方程与流固耦合条件联合求解,即可得到反射声压和透射声压。
假设Wi和Wt分别为入射声功率和透射声功率,蜂窝夹层板的传声损失(sound transmirrion loss,STL)或隔声量可定义为
(27)
式中,入射声功率和透射声功率可表示为
(28)
式中:vi=pi/(ρ0c0)、vt=pt/(ρ0c0)表示流体质点的速度;Re表示取实数结果;*表示复数共轭。
2 数值计算与仿真
为了验证理论模型的正确性,通过有限元软件COMSOL对负泊松比蜂窝夹层板声振特性进行仿真模拟。
如图1所示的模型,其中负泊松比蜂窝夹层板的几何参数为:a=207.85 mm、b=170.01 mm、hmax=10 mm,上下面板最大厚度均为h1=2 mm。如图2 (a)所示,负泊松比蜂窝芯层的相关尺寸为:hc=6 mm、l1=10 mm、l2=20 mm、tc=1 mm、θ=30°。变厚度负蜂窝夹层板均由铝组成,其材料性能为:Es=70 GPa、vs=0.3、ρs=2 700 kg/m3。
令蜂窝夹层板厚度变化系数ξ1=0、ξ2=0,截断系数M=N=8,得到了等厚度蜂窝夹层板在四边简支边界条件下的前5阶固有频率的理论结果,如表1所示,表中也列出了文献[4]和有限元方法的结果。从表中可以看到,与理论结果及文献[4]的结果相比,有限元仿真得出的结果较大,其原因是建模时选择蜂窝为等效模型,但三者误差最大不超过3%,其误差在允许范围内。而且在表2中,有限元与理论的前5阶模态振型相同,由此可以看出所建立的蜂窝夹层板的理论模型是准确有效的。

表1 蜂窝夹层板前5阶模态固有频率对比Table 1 Comparison of the first five orders of intrinsic frequency of honeycomb sandwich plates Hz
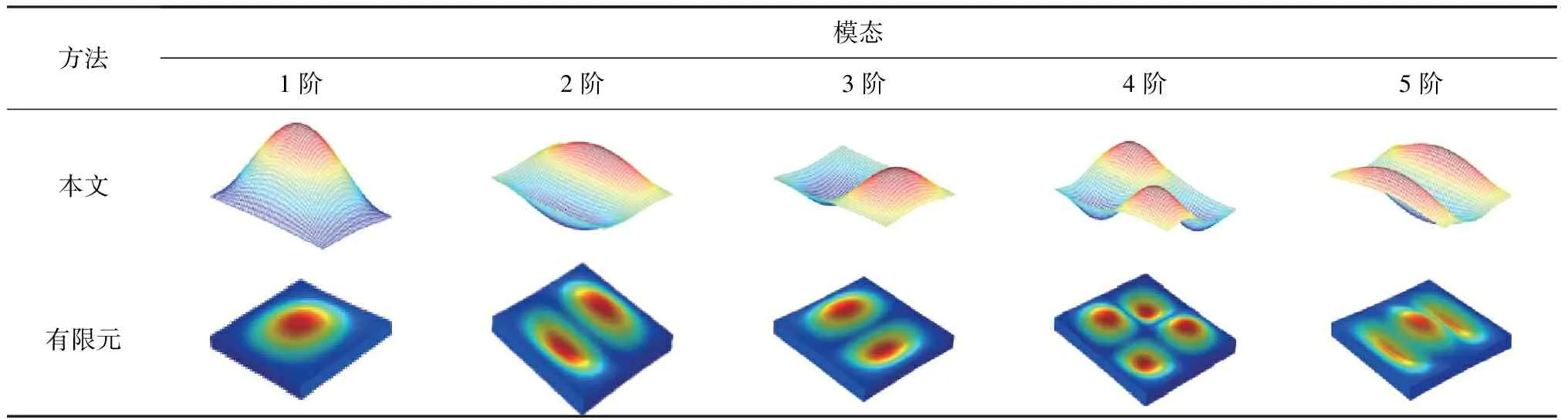
表2 四边简支条件下理论与有限元计算的前5阶模态振型对比Table 2 Comparisons of the first five mode shapes computed by the present theory and finite element under simply supported condition
使用有限元建模仿真,验证所建立的蜂窝夹层板隔声理论模型的正确性。在计算中,声波垂直入射,取简谐声波入射方位角ψ1=0°、ψ2=0°,入射声压振幅p0=1 Pa。图3给出了理论与有限元分析在四边简支边界条件下蜂窝夹层板的隔声特性曲线,可以看出两者吻合良好。

图3 等厚度蜂窝夹层板隔声曲线对比Fig.3 Comparisons of sound insulation curves for honeycomb sandwich plate with equal thickness
3 参数变化的影响
基于所建立的变厚度负泊松比蜂窝夹层板理论模型,在保证其余参数不变的情况下,通过控制变量,选取蜂窝夹层板的前5阶频率范围1 000~7 000 Hz,研究特征角、厚度变化系数及边界条件对隔声特性的影响。
特征角是影响蜂窝材料特性的一个重要参数,其对蜂窝结构的性能有较大影响,从而影响结构的隔声性能。图4为不同特征角等厚蜂窝夹层板的隔声曲线。特征角为θ=0°和θ=-30°的蜂窝夹层板隔声性能类似,相比较于θ=30°的负泊松比蜂窝夹层板隔声曲线,可以看出在低频时变化不大,高频时变化更加明显,其波谷略有右移,波谷频率有所增大。

图4 特征角对蜂窝板隔声性能影响Fig.4 Effect of characteristic angle on sound insulation of honeycomb plates
图5为四边简支边界条件下不同变厚度负泊松比蜂窝夹层板的隔声曲线。当ξ1=1、2,ξ2=0时为沿x轴方向单向变厚度负泊松比蜂窝夹层板,当ξ1和ξ2分别等于0.5、1时为沿x、y轴方向双向变厚度负泊松比蜂窝夹层板。可以看出,无论是单向还是双向变厚度蜂窝夹层板,隔声波谷均随着厚度变化系数的增大而左移,高频范围变化幅度较大。且在单双向系数增大时,出现了更多的波谷,表明过薄的上下面板会导致蜂窝夹层板的隔声效果降低。

图5 厚度变化系数对负泊松比蜂窝板隔声性能影响Fig.5 Effect of thickness variation coefficient on sound insulation of honeycomb plates with negative Poisson′s ratio
图6给出不同边界条件下,x轴单向变厚度负泊松比蜂窝夹层板的隔声曲线。图中各边界条件分别为四边简支(SSSS),对边固支、另一对边简支(CSCS),四边固支(CCCC)。可以看出,随着边界弹簧刚度的逐渐提高,隔声曲线逐渐右移,其隔声频率范围越大。这与其固有频率的变化规律一致。

图6 边界条件对负泊松比蜂窝板隔声性能影响Fig.6 Effect of boundary conditions on sound insulation of honeycomb plates with negative Poisson′s ratio
4 结束语
采用一阶剪切变形理论和改进的瑞利-里兹法,将位移场展开为带辅助函数和余弦函数的傅里叶级数,结合流固边界耦合条件,建立了蜂窝夹层板隔声理论模型。通过有限元分析和文献验证了理论的准确性。在此基础上,分析了参数变化对隔声特性的影响。结果表明,特征角对蜂窝夹层板的隔声效果在低频时影响不大;不同厚度变化系数对于系统的隔声影响较大,过薄的蒙皮会导致出现新的波谷,从而导致隔声效果大幅降低;而随着弹性约束刚度的增大,即边界条件约束增大,系统的隔声效果逐渐提高,隔声频率范围增大。本研究中,变厚度蜂窝结构可进一步运用于水下环境,分析其流体深度、内支架位置、厚度变化系数等对系统的振动和隔声性能影响。

