基于ELM-AE和BP算法的极限学习机特征表示方法
苗军,刘晓,常艺茹,乔元华
(1.北京信息科技大学 网络文化与数字传播北京市重点实验室,北京 100101;2.北京工业大学 应用数理学院,北京 100124)
0 引言
单隐层前馈神经网络(single-hidden layer feedforward neural network,SLFN)是一个简单的三层网络结构,由输入层、隐藏层和输出层组成。SLFN具有泛逼近性,可以逼近复杂的非线性函数,也可以对经典参数化技术难以处理的自然和人工合成数据进行建模,因此在许多领域得到了广泛的应用。
极限学习机(extreme learning machine,ELM)是一种SLFN学习算法,因其学习速度快、泛化能力强,被广泛应用于发动机转速控制[1]、RNA识别[2]、蛋白质交互预测[3]、故障诊断[4-5]、图像编码[6]、自动降噪[7]和储能系统选址[8]等领域。
在训练阶段,ELM首先用随机值初始化其三层全连接网络的参数,然后使用最小二乘法解析计算网络输出权重,且不对输入权重修改和学习,使之始终保持随机初始化值。在测试或运算阶段,ELM首先通过Sigmoid非线性激活函数获得隐藏层的响应,然后该响应由隐藏层映射到输出层,后面这一层映射可视为一个线性系统[9]。因此,ELM的本质是求解线性系统,即在最大程度地减少训练误差的同时确定输出权重[10]。
为了达到理想的性能,ELM通常需要有大量的隐藏节点,这增加了计算成本,容易导致训练后的模型过拟合。有2种方法可以有效地减少隐藏节点的数量:1)基于在线增量式,例如进化ELM[11];2)基于剪枝的方法,例如最优剪枝ELM(optimally pruned ELM,OP-ELM)[12]。此外,针对随机生成的参数缺乏紧凑性,Yu等[13]使用基于梯度的方法对ELM中输入层到隐藏层的参数进行更新,在少量隐藏节点上实现更好的性能。Kasun等[14]利用极限学习机自编码器(ELM based autoencoder,ELM-AE)学习特征表示,有助于对深层ELM的输入权重进行初始化。Zhu等[15]提出了约束ELM(constrained ELM,C-ELM),并将输入权值约束作为训练数据中类间样本的一组差分向量。Tapson等[16]所选的输入层权重是随机的,但偏向训练数据样本,该方法称为计算输入权重ELM(computation of input weights ELM,CIW-ELM)。McDonnell等[17]提出了形状化输入权重,并结合了不同的参数初始化方法来探索紧凑性。本文重点研究了基于误差反向传播(back propagation,BP)和自编码器(autoencoder,AE)进行ELM参数初始化的方法,在文献[14]的基础上,提出一种新的学习训练方法,不仅获得了更紧凑的参数,而且以更少的隐藏节点和时间获得了更好的性能。
1 ELM-AE
1.1 极限学习机
ELM是一个三层全连接网络。在ELM中,输入层和隐藏层之间的权值参数是随机生成的,而隐藏层和输出层之间的权重值通过最小二乘法获得的解析表达式进行求解。也就是说,在ELM中唯一需要学习的就是输出权重,且学习过程不需要迭代计算权重,因此具有高效的学习效率。
对于一个输入样本x,ELM输出单元的响应值所组成的输出向量由下式定义:
式中:L为隐藏层节点个数;βi为第i个隐单元指向所有输出单元的连接权向量;β=[β1,β2,…,βL]为输出权重;h(x)=[h1(x),h2(x),…,hL(x)]为输入样本x在隐藏层上的响应向量,可以看作是ELM的特征空间,其中第i个隐单元对于输入样本x的响应值为
hi(x)=f(wix+bi)i=1,2,…,L
(1)
式中:wi为输入层所有输入单元指向第i个隐单元的连接权向量;bi为第i个隐单元的偏置或门限阈值;f为隐单元的激活函数,通常取Sigmoid函数。在ELM中wi和bi的值在模型训练开始前经随机初始化后就始终保持不变,测试阶段也采用相同的值。
N个输入样本x1、x2、…、xN在隐藏层上的N个响应向量组成了一个隐藏层响应矩阵H=[h(x1),h(x2),…,h(xN)]T。同理,N个输入样本在输出层上的N个输出向量组成了一个输出矩阵O=[o(x1),o(x2),…,o(xN)]T,因此有如下等式:
Hβ=O
(2)
在监督学习的情形下,ELM直接令输出矩阵O等于由N个样本的标签向量t(x1)、t(x2)、…、t(xN)所组成的标签矩阵T,T=[t(x1),t(x2),…,t(xN)]T,即O=T,则得到:
Hβ=T
(3)
这样输出权重β能够由下式来计算:
β=H†T
(4)
式中:H†为关于矩阵H的Moore-Penrose广义逆矩阵[18]。
ELM的训练算法如下[19]:
步骤1:随机分配输入权重wi和偏置bi,i=1,2,…,L。
步骤2:计算N个样本的隐藏层响应矩阵H:
步骤3:通过式(4)求解输出权重β。
1.2 基于ELM的自编码器
当设置极限学习机ELM的期望输出t=x时,即将式(3)中的期望输出矩阵T换成输入样本矩阵X时,就得到了如下公式:
Hβ=X
(5)
式(5)意味着让ELM的输出t以无监督的方式重构输入数据x,即通过重建输入样本来学习样本的无监督重构特征表示[5],那么ELM经过学习训练后的输出权重β可以看作是原始输入数据x的特征重构矩阵。此时的ELM称之为基于极限学习机的自编码器(ELM-AE)。把ELM-AE的输出权重β用βELM-AE表示,由式(4)可得到求解公式:
βELM-AE=H†X
(6)
由于t=x,所以ELM-AE的输入层和输出层的单元数目相同。
2 权重微调的ELM-AE
如1.1节所述,ELM的输入权重W在用随机值初始化后始终保持不变,ELM在学习训练的过程中不对其进行更新。这样虽然能节省ELM学习训练的时间,但由于输入权重是随机值,使得ELM在测试时并不能取得很好的效果。主要原因是随机确定从输入层到隐藏层的连接权重,导致ELM的特征表示不紧凑,即指在随机映射的过程中,输入向量通过映射到隐层空间所得到的隐单元响应值h(x)在特征映射方向的确定上具有随机性。
在ELM-AE中,通过非监督方式可以对输入样本学习较好的特征表达,这种表达由原来随机的特征方向映射统一到一个基于输入数据的映射方向。Kasun等[14]发现,通过ELM-AE得到的特征能够减少类内距离,增大类间距离。不过这种特征映射没有引入类别标签信息,缺少了类别信息来约束表达数据的判别性。
为了解决这一问题,本文提出了基于权重微调的极限学习机自编码器(简称微调ELM-AE)。下面以图1所示的示例性神经网络对训练过程进行说明。
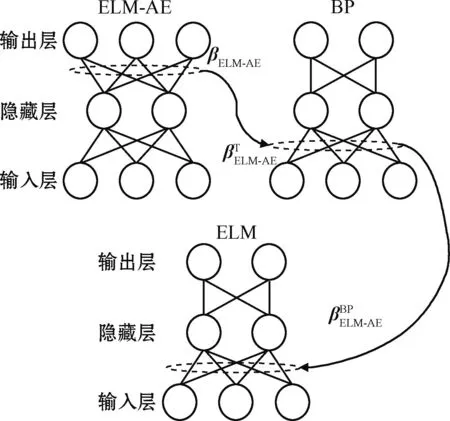
图1 微调ELM-AE的训练过程Fig.1 Training procedure of fine-tuned ELM-AE
第一步,采用非监督学习方式得到ELM-AE网络的输出权重。
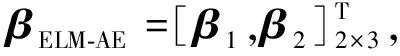
第二步,采用监督学习的方式对ELM-AE网络学习到的权重进行微调更新。
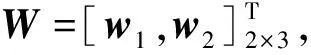
然后,使用ELM-AE学习到的权重βELM-AE来初始化BP神经网络从输入层到隐藏层的权重W,即:
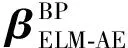
第三步,用微调的ELM-AE权重初始化一个ELM的输入权重,并采用最小二乘算法训练ELM用于分类。
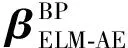
然后,通过前馈运算和最小二乘求解,得到ELM隐藏层的响应值和输出权重:
式中:b为隐单元的偏置;βELM为ELM的输出权重。
3 实验
在没有任何失真的原始MNIST手写数字数据集[20]上进行分类实验,使用所有60 000个训练样本来训练模型,并使用10 000个测试样本来评估性能。实验在台式计算机上进行,该台式计算机具有运行在MATLAB R2014a中的核心i7-4770 3.4 GHz处理器和32 GB RAM。
3.1 性能实验
MNIST数据集样本图像的大小是28×28像素,包含10类数字样本,因此本实验中模型的输入节点数是784,输出节点数是10。为了评估微调ELM-AE的性能,分别使用微调ELM-AE与其他方法初始化ELM,并对分类结果进行比较。对比方法如下:
1)ELM。随机选择输入权重和偏差。
2)ELM-AE。使用ELM-AE输出权重的转换来初始化ELM的输入权重,随机选择偏差。
3)BP。首先使用随机参数训练BP网络,然后使用调整后的参数(输入权重和偏差)来初始化ELM[13]。
4)自编码器。首先训练自编码器来学习原始数据的特征表示,然后使用学习到的参数来初始化ELM输入权重和偏差。
结果如图2所示。可以发现BP、自编码器和微调ELM-AE的测试分类准确率曲线几乎相同,且优于ELM和ELM-AE。BP、自编码器和微调ELM-AE的平均准确率分别为97.66%、97.75%和97.81%。这表明微调ELM-AE的性能更优。
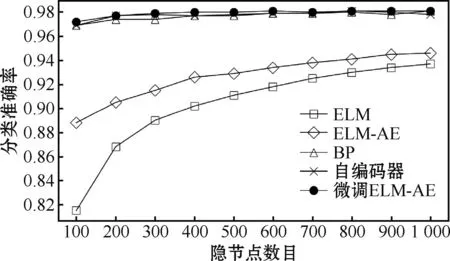
图2 测试分类准确率曲线Fig.2 Curves of test classification accuracies
3.2 计算成本对比
以97.6%的测试准确率为例,对比5种方法为了达到相似的测试准确率所需要的隐藏节点数量和时间,结果如表1所示。
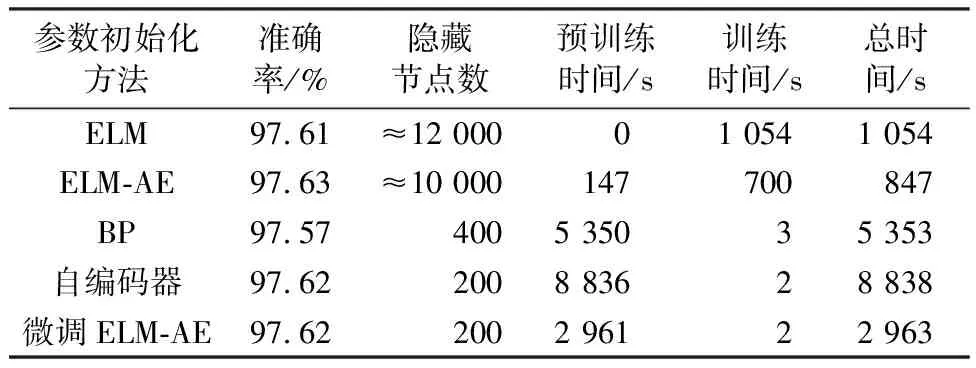
表1 相似测试准确率的计算成本比较Table 1 Computation cost comparison with similar test accuracies
从表1可以看出,ELM和ELM-AE达到目标准确率的总时间最少,但所需隐藏节点数量均超过10 000个,并且这2种方法的训练时间远高于其他方法。相比之下,经过微调的ELM-AE只需要200个隐藏节点就可以获得目标准确率,并且其时间主要花费在预训练阶段,训练时间只需2 s。
3.3 深层结构实验
ELM-AE可以看作是一个双向无监督学习神经网络。利用这一性质,可将微调的ELM-AE作为基本模块两两堆叠成深层全连接神经网络,这种结构可称为堆叠的微调ELM-AE(stacked fine-tuned ELM-AE,SFEA)。
将SFEA与多隐藏层前馈神经网络(multiple-hidden layer feedforward neural network,MLFN)和堆叠式自编码器(stacked autoencoder,SAE)[21]进行对比。这3个模型都为多层全连接神经网络结构,包含1个输入层、3个隐藏层和1个输出层,各层的节点数为784、1 000、1 000、1 000、10。在SFEA中,使用ELM-AE初始化前4层之间的参数,然后使用BP对深层结构进行微调。最后,使用微调参数以相同的结构初始化ELM,即使用前4层提取特征,然后使用最小二乘法确定输出权重。MLFN和SAE由BP网络训练。
此外,选择主流的非全连接多层神经网络:卷积深度学习模型LeNet-5[20]、ResNet-34[22]和DenseNet[23]与本文方法进行对比。实验结果如表2所示。SFEA的性能好于MLFN,并与SAE和其他卷积深度学习模型可比。这表明经过微调的ELM-AE可以作为深层结构的一个可供考虑的组件,以帮助构建深层全连接神经网络。

表2 深层结构实验结果Table 2 Experimental results on deep structures
4 结束语
本文集中使用无监督和监督的方法进行ELM的初始化,即使用无监督的ELM-AE将参数初始化从随机特征空间限制到有限的输入空间,产生了紧凑的特征表示;使用有监督的BP算法来微调ELM-AE权重,在特征表示中增加了区分度,使特征表示具有判别性。实验结果表明,与对比方法相比,本文提出的方法在时间消耗类似的情况下,节省了存储空间,综合性能最优。

