能耗优化的移动机器人路径规划方法
李晓东,童亮,2,3,陈梓宁,张博文,章者一
(1.北京信息科技大学 机电工程学院,北京 100192;2.新能源汽车北京实验室,北京 100192;3.北京电动车辆协同创新中心,北京 100192)
0 引言
目前,移动机器人在各行各业的应用越来越广泛,如果园机器人[1]、抢险救灾机器人[2]、医疗服务机器人[3]和家庭服务机器人[4]等。移动机器人的工作环境不再仅仅是平坦开阔的道路,也可能包含动、静态障碍物或凹凸不平的路面。移动机器人通常由便携式能源驱动,一次性携带的能量有限。因此,如何使移动机器人以最小的能耗代价,无碰撞地到达目的地越发重要。基于能耗优化的最优路径规划方法是解决这一问题的有效手段。通常移动机器人路径规划分为全局规划和局部规划。
目前的路径规划算法有很多,如用于静态全局规划的Dijkstra算法[5]、Floyd算法[6]和A*算法[7-8]等。而局部路径规划则需要根据机器人的运动约束生成期望的控制量,如动态局部路径规划的动态窗口法(dynamic window approach,DWA)[9-10]、蚁群算法[11]和人工势场法[12]等。其中,A*算法应用尤为广泛。顾青等[13]提出一种基于改进A*算法的电动车能耗最优路径规划方法,但是没有综合考虑避障问题。刘靖等[14]以改进A*算法为基础,提出了一种节能、安全且通用的移动医疗机器人无碰撞路径规划方法,但是没有考虑坡度,只适用于平坦路面且只能通过静态障碍物。潘富强等[15]提出了一种基于改进A*算法与改进动态窗口法的融合算法,解决了动、静态障碍物避障问题,但是没有考虑能耗。Pal等[16]提出了EA*算法,通过减少移动机器人转弯次数降低能量损耗,但是没有考虑地面摩擦、坡度等因素对路径规划的影响。Ganganath等[17]基于A*算法提出了一种在不平坦路面上生成节能路径的新算法,这种三维算法虽然生成路径较为准确却极大地增加了计算量,进而增加了规划时间,而且它没有考虑能量回收,也不能通过动态障碍物。Lanthier等[18]引入了地形面权重概念,该概念分析了地形、摩擦和每个地形面坡度的不同特性,利用Dijkstra算法在图中以最小的总权值进行寻径,但是容易陷入局部最优解。
本文通过优化A*算法、融合改进DWA算法等方法,为解决能耗最优路径规划问题提供了一种新思路。
1 A*算法优化
1.1 传统A*算法性能分析
A*算法是一种常用的路径查找和图形遍历算法,能够完成机器人从起始点到目标点的静态路径规划。它有较好的性能和准确度,算法中的距离估算值与实际值越接近,最终搜索速度越快。传统A*算法的代价函数如式(1)所示:
f(n)=g(n)+h(n)
(1)
式中:n为当前节点;f(n)为总代价;g(n)为起点到当前节点的实际代价;h(n)为当前节点到目标节点的估计代价。
相对于其他搜索算法,A*算法的搜索速度较快,因为它能够通过启发式函数来减少搜索的路径数。这使得A*算法在处理大规模搜索问题时非常高效。但是,传统A*算法只能求解最短路径,不能满足能耗最优规划需求。因此,本文在传统A*算法基础上引入能耗影响因子、优化代价函数,实现在不平坦路面上基于能耗最优的路径规划。
1.2 优化代价函数
为了表征在不平坦路面上机器人的移动距离和能量消耗,Mejri等[19]构建了基于距离的邻接矩阵与基于能量的邻接矩阵。本文基于此方法构建邻接矩阵,将移动机器人行驶时的能耗转化为能耗代价,赋予在二维栅格地图上。本文采用文献[17]的方法,构建地形图,如式(2)所示:
(2)
式中:z(x,y)为移动机器人所处高度;(x,y)为移动机器人所在坐标。本文在此地形图基础上进行能耗最优路径规划。首先,对机器人运动进行受力分析,计算出能耗代价。研究对象为四轮后驱轮式移动机器人,机器人在运动过程中始终保持匀速且速度较低,忽略空气阻力和加速阻力。机器人上坡时的受力分析如图1所示。图中,Ft为驱动力,Ff为滚动阻力,Fg为坡度阻力,Fs为支持力,G为机器人所受重力,φ为道路坡度。
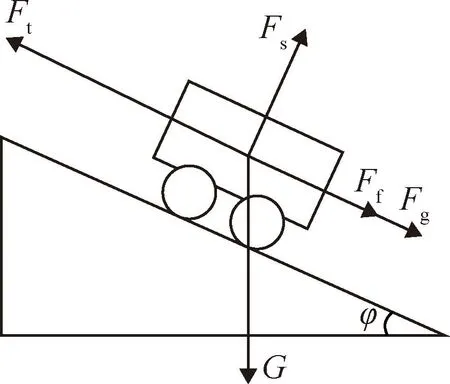
图1 移动机器人物理模型Fig.1 Physical model of mobile robot
当移动机器人处于上坡阶段时,当前节点高度大于上一个节点高度(zx>zx-1),建立机器人行驶受力方程式:
Ft=Ff+Fg
(3)
机器人在运动过程中始终保持匀速且速度较低,忽略空气阻力和加速阻力,可得:
(4)
式中:T为电动机输出扭矩;ig为变速器传动比;i0为主减速器传动比;ηT为传动系统机械效率;r为车轮半径;f为滚动阻力系数。φ由式(5)计算得到。
(5)
由式(4)可得:
(6)
根据电机的转速特性,电机的功率Pi和与扭矩T、转速n之间的关系为
(7)
其中,电机转速n与机器人行驶速度v之间的关系为
(8)
则在上坡工况下,驱动电机在等速行驶时间Δt内所消耗的电能为
(9)
其中,行驶路程Δs为
(10)
联立式(6)~(9)可得在上坡路段任意两节点间的能耗为
Ei=(Gfcosφ+Gsinφ)Δs/ηT
(11)
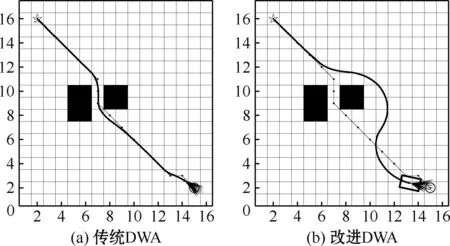
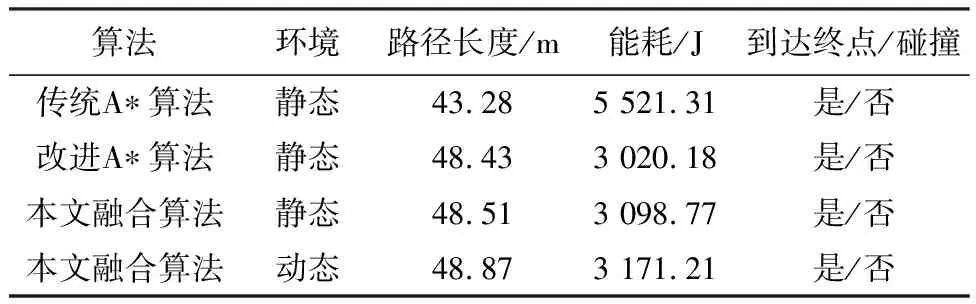
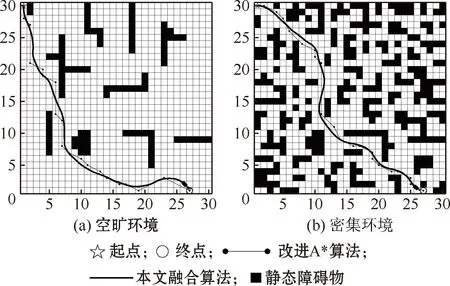
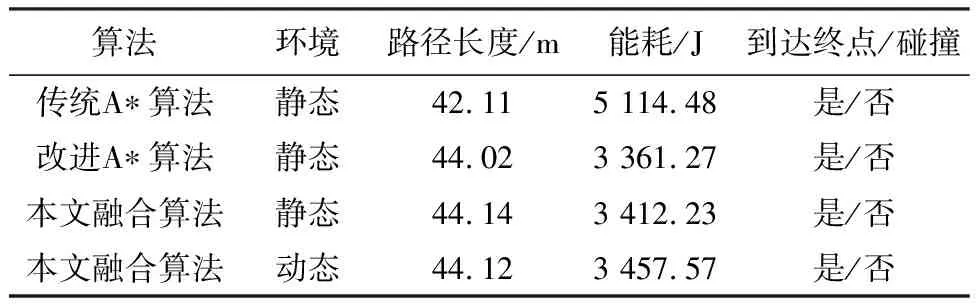
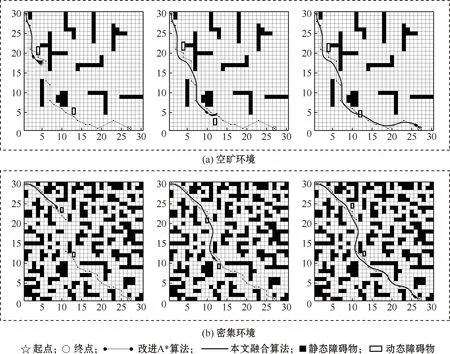
当机器人下坡时(zx ①当Ff≥Fg时,不需要制动,则在此工况下,任意两节点间的能耗为 Ej=(Gfcosφ-Gsinφ)Δs/ηT (12) ②当Ff (13) 式中:k为制动回收系数。回收的电能为 Ej1=k(-Gfcosφ1+Gsinφ1)Δs1/ηT (14) 式中:φ1为在进行制动回收时的道路坡度; Δs1为制动回收时的行驶路程。 综上,移动机器人在路段((x-1),x)行驶时的能耗为 (15) 由此可计算起始点到当前节点的能耗代价Qcur(n)和当前节点到下一个子节点的能耗代价Qnext(n)。为了实现在考虑能耗的情况进行路径规划,在传统A*算法的代价函数式(1)的基础上增加能耗代价,并分别赋予权重因子a、b、c、d,形成新的代价函数: f(n)=ag(n)+bh(n)+cQcur(n)+dQnext(n) (16) 式中:a、b、c、d为正常数。 传统A*算法的路径搜索方式为4邻域4方向和8邻域8方向,搜索方向少,移动范围小。齐款款等[20]采用24邻域16方向的搜索方式,较前者搜索视野范围更大,能够更快地找到最优解,如图2所示。 图2 24邻域16方向搜索方式Fig.2 24 neighborhood 16 direction search mode 本文在此基础上对搜索方向进行优化。当机器人向前行驶时,其后方附近的5个搜索方向使用极少。因此,为了进一步提高算法规划效率,可以将其舍弃,将16个搜索节点方向改为11个。判断依据为当前节点和拓展子节点的连线与当前节点和目标点连线的夹角α大小,具体规则如表1所示。 表1 优化搜索方向规则Table 1 Search direction optimization rule A*算法规划出来的路径不够平滑且不能通过动态障碍物。为解决这一问题,本文将其与改进DWA算法进行融合。但是,A*算法规划出来的路径经常出现相邻的多个节点处于同一直线上,若直接将所有节点作为DWA子目标进行局部路径规划,会增加很多不必要的计算。为了进一步提高整体算法效率,可以通过比较节点间的转角度数,删除中间多余节点,继而以剩余节点作为局部规划的子目标。 动态窗口算法是一种基于预测控制理论的路径规划方法,一般用于局部路径规划,能够有效避开动态障碍物。其根据机器人的运动状态,在控制空间中离散采样多组速度、角速度,并以此为基础预测下一个或者多个采样时刻机器的行走轨迹,并根据评分规则对其进行打分(评分内容包括与障碍物的距离、朝向终点的角度等),由此选出当前的最佳位置,再由此位置继续重复以上过程建立新的窗口,如此循环直至到达目标点。 假设机器人当前位置为(xt-1,yt-1)、航向角为θt-1,选取评分最高的速度v、角速度ω。由于采样时间间隔Δt很短,可假设机器人在Δt内做匀速直线运动,由此可计算出移动机器人下一时刻的位置信息,建立移动机器人运动模型: (17) 为使模型不断循环到达终点,需要在控制空间中不断进行采样,控制空间的设定主要取决于速度、角速度和不发生碰撞的最小距离。 2.2.1 速度边界 根据移动机器人的机械结构和环境需求等,可设立速度边界Vm为 Vm={(v,ω)|v∈[vmin,vmax],ω∈[ωmin,ωmax]} (18) 式中:vmin、vmax分别为机器人线速度上下界;ωmin、ωmax分别为机器人角速度上下界。 2.2.2 加速度边界 考虑到机器人驱动电机、转向电机性能等问题,存在加速度边界Vd为 Vd={(v,ω)|v∈[vc-avmaxΔt,avmaxΔt], ω∈[ωc-aωmaxΔt,aωmaxΔt]} (19) 式中:vc、ωc分别为移动机器人当前时刻的线速度和角速度;avmax、aωmax分别为移动机器人最大线加速度和最大角加速度。 2.2.3 障碍物边界 为避免与动静态障碍物发生碰撞,需要对机器人和障碍物之间的距离进行约束。障碍物边界Va可设为 (20) 式中:d(v,w)表示当前速度下对应模拟轨迹与障碍物之间的最小距离。 为兼顾上述3个边界限制,取3个控制空间的交集作为速度采样空间,即: Vs=Vm∩Vd∩Va (21) 采样完成后,根据不同的速度、角速度生成不同的模拟轨迹,对每条轨迹进行评分,取得分最高者为下一时间段规划轨迹。评分规则由评价函数确立。评价函数如式(22)所示: G(v,ω)=σ(α·h(v,ω))+σ(β·d(v,ω))+σ(γ·o(v,ω)) (22) 式中:σ表示归一化;h(v,ω)为方位角评价函数,用预测轨迹末端朝向和目标点方向夹角Δθ或(180-Δθ)来计算;d(v,ω)为距离评价函数,以模拟轨迹与障碍物之间的最近距离大小来评估;o(v,ω)为速度评价函数,以模拟轨迹所对应的线速度大小来评估;α、β和γ均为评价函数的系数。 2.4.1 引入机器人尺寸 传统DWA算法没有考虑机器人实际尺寸,而是粗略地以轨迹与障碍物之间的最近距离作为碰撞约束生成,当机器人以此路径实际行驶时容易出现碰撞情况。为解决这一问题,本文引入移动机器人尺寸信息,根据机器人几何中心坐标和尺寸信息计算出4个顶点的坐标,根据这4个点生成矩形轮廓,然后离散化生成轮廓点集,并计算点集内的点和障碍物之间的距离D(v,ω),归一化后,取代d(v,w)写入评价函数,以移动机器人轮廓和障碍物之间的距离为基准评价路径的优劣。如图3所示。 图3 狭窄路段A*融合DWA路径规划Fig.3 Narrow section A* fusion DWA path planning 当不考虑机器人尺寸或机器人尺寸较小时通过狭窄通道;当机器人尺寸较大时选择绕路,确保机器人以此路径行驶时不会发生碰撞。 2.4.2 增加半径约束 考虑到移动机器人的机械结构,路径应满足机器人的最小转弯半径要求。因此,将转弯半径作为约束条件归一化后加入评价函数来评估轨迹。转弯半径为 (23) 优化后的评价函数为 G(v,ω)=σ(α·h(v,ω)+β·D(v,ω)+γ·o(v,ω)+δ·r(v,ω)) (24) 式中:δ为评价函数的系数。 动态窗口法具备良好的局部避障能力,但是容易陷入局部最优解。本文将A*算法与动态窗口法相结合,既能得到全局最优解,又具备局部避障的能力。融合改进A*算法和DWA算法的路径规划算法流程如图4所示。 图4 融合算法流程Fig.4 Flow chart of fusion algorithm 为验证本文改进A*算法的可行性和有效性,在空旷和密集2种环境下分别用传统A*算法、文献[13]算法、文献[20]算法与本文改进A*算法进行对比仿真实验。其结果如图5~6所示,具体数据如表2~3所示。为了更直观地对比本文改进A*算法与其他方法,对性能指标进行归一化以直方图形式表示,如图7所示。 表2 A*算法空旷环境下仿真数据Table 2 Simulation data of A* algorithm in open environments 表3 A*算法密集环境下仿真数据Table 3 Simulation data of A* algorithm in dense environments 图5 空旷环境下规划的路径轨迹Fig.5 Path trajectories planned in open environments 图6 密集环境下规划的路径轨迹Fig.6 Path trajectories planned in dense environments 图7 多指标归一化分析Fig.7 Multi-index normalization analysis 从仿真结果可知,在空旷环境下相较于传统A*算法,文献[13]的算法节约了大约16.72%的能耗;文献[20]由于增加了搜索邻域,搜索范围更大,搜索效率更高,相较于传统A*路径和文献[13]路径节点数更少、路径更短、拐角数和转角和更小、路径更为平滑,但是由于没有考虑能耗,比文献[13]耗能更多;本文改进A*算法在文献[20]的基础上进一步优化了搜索方向,搜索效率更高的同时保证了能耗最小,相较于传统A*路径节约了大约45.30%的能耗,相较于文献[13]节约了大约34.32%的能耗。而在密集环境下,本文改进A*算法仍然保持着优越的性能,在保证更高的搜索效率的同时,相较于传统A*算法节约了大约34.28%的能耗,相较于文献[13]节约了大约27.03%的能耗,相较于文献[20]节约了大约32.84%的能耗。综合来看,本文所提出的改进A*算法能够为机器人规划出更为高效的全局节能路径。 为了进一步验证本文所提融合算法的可行性,在空旷环境和密集环境下分别进行仿真实验,并和传统算法进行对比分析。结果如图8~9所示,具体数据如表4~5所示。 表4 空旷环境下各算法仿真数据Table 4 Simulation data of each algorithm in open environments 图8 静态环境下的仿真路径Fig.8 Simulation path in static environments 由图8、表4和表5可以看出,不论是空旷环境还是密集环境,融合算法都能很好地完成规划任务,解决了A*算法生成路径不平滑的问题。但是平滑后的路径和原始能耗最优路径有微小的偏差,使得能耗相对于改进A*算法分别增加了约2.60%、1.52%,但是相对于传统路径分别节约了大约43.88%、33.28%,仍然可观。图9中(a)、(b)的第一张图均为通过第一个动态障碍物时的场景,第二张图均为通过第二个动态障碍物时的场景,第三张图均为到达终点时的场景。图9中的2个动态障碍物分别以0.80 m/s、0.50 m/s的速度做往返运动,而同样地由于机器人需要躲避动态障碍物,路径也有一定的偏移,但是由于本文以机器人轮廓到障碍物的距离取代路径到障碍物的距离作为距离评价函数,并增加了转弯半径约束,所以避障更为灵活、精准,路径偏移量不大且较为平滑,在空旷和密集环境能耗相对于传统A*路径分别节约了42.56%、32.39%。算法规划任务完成良好,能够很好地适应复杂的动、静态环境,有效地解决了改进A*算法的动态避障问题。 表5 密集环境下各算法仿真数据Table 5 Simulation data of each algorithm in dense environments 图9 动态环境下的仿真路径Fig.9 Simulation path in dynamic environments 针对移动机器人在能量有限的情况下的路径规划需求,本文提供了一种新的基于全局能耗最优的动静态避障规划思路,并仿真验证了其可行性与有效性。主要工作有以下3个方面: 1)基于摩擦阻力、坡度等因素,建立能耗模型,增加A*搜索邻域并优化其搜索方向,提出一种同时考虑最短距离和能耗的搜索方式,规划出全局最优路径。 2)提出新的距离评价函数D(v,ω),增加转弯半径约束,改进DWA算法。 3)以删除多余中间节点以A*剩余节点作为DWA子目标的方式,融合改进A*算法和改进DWA算法,使机器人具有在复杂的动静态环境中避障的能力。 本文融合算法有效地解决了机器人在复杂环境下的规划需求,具有一定实用价值。但是改进DWA算法只在全局规划时考虑了能耗,而在进行局部规划时未能把能耗考虑进去,后续工作将重点研究考虑能耗评价的局部路径规划。1.3 搜索邻域和搜索方向的优化
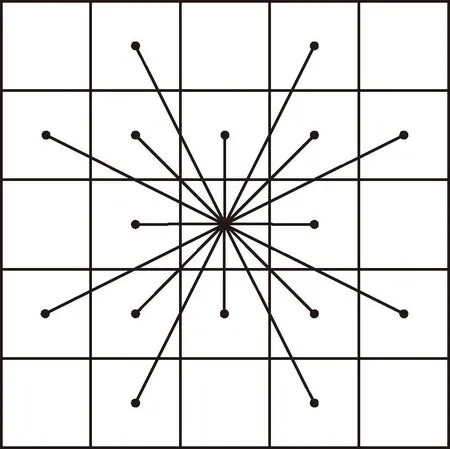

1.4 删除多余共线点
2 DWA算法改进
2.1 移动机器人运动模型的建立
2.2 速度采样
2.3 轨迹评价
2.4 评价函数的优化
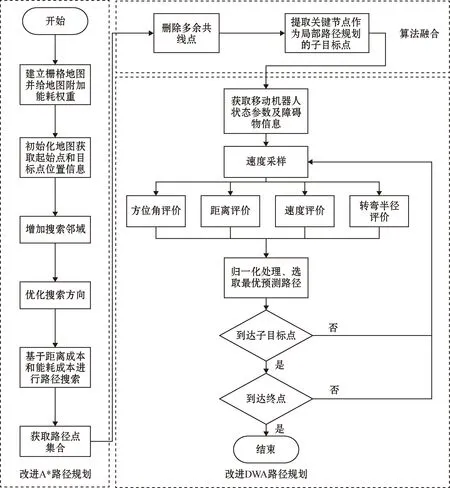
3 仿真实验与分析
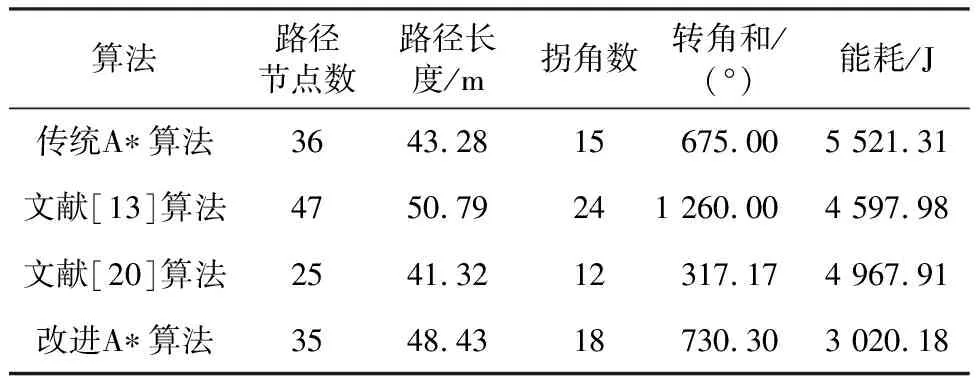
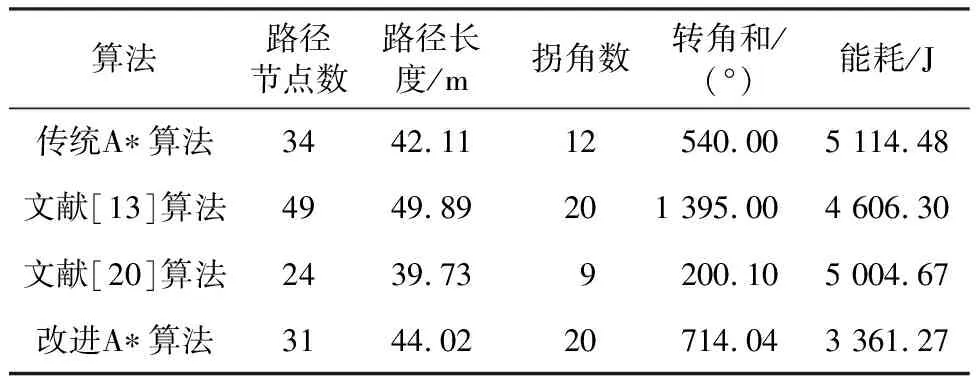
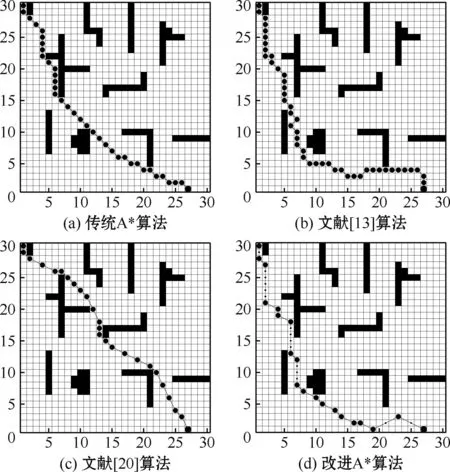
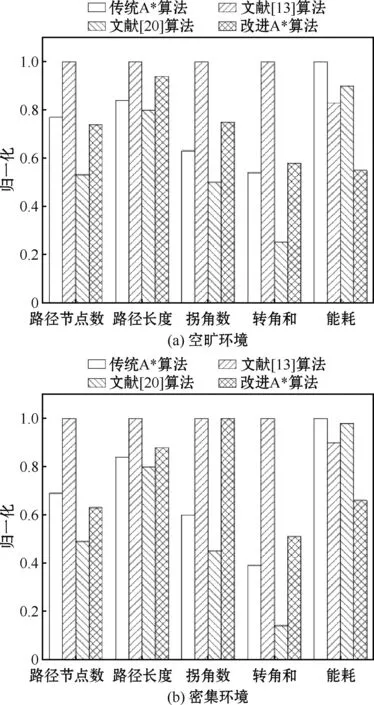
3.1 A*算法的对比分析

3.2 融合算法仿真分析
4 结束语

