用求导法解决极值问题

郝 详

(河北保定外国语学校 河北 保定 071000)

极值问题在物理教学中经常出现,根据物理规律,找到物理量之间的关系,利用数学知识求解极值,是摆在每个物理教师面前的问题.

在求解极值问题时,最长用的方法是三角函数法(在2022 年 1 月浙江省普通高校招生选考科目考试物理试题第5题用到)和二次三项式性质法(配方法,比如2012年普通高等学校招生全国统一考试浙江理综物理卷第5题用到).但是,这两种方法对有的题目效果并不好,比如下面的例题.

【例1】如图1所示,光滑小球a、b的质量均为m,a、b均可视为质点,a、b用刚性轻杆连接,竖直地紧靠光滑墙壁放置,轻杆长为l,b位于光滑水平地面上,a、b处于静止状态,重力加速度大小为g.现对b施加轻微扰动,使b开始沿水平面向右做直线运动,问:直到a着地的过程中,何时b的速度最大?

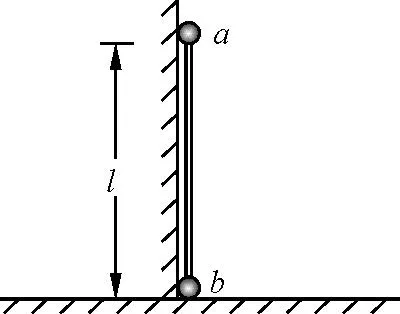
图1 例1题图

分析:对b施加轻微扰动使b开始沿水平面向右做直线运动,杆被压缩,对a和b均为推力,杆对a做负功,杆对b做正功,当杆的推力等于零时,杆对b做正功最多,此时b的速度最大,设杆与水平方向的夹角为θ,对系统由机械能守恒有

沿着杆的速度相等,有

vasinθ=vbcosθ

联立解得

即

Ekb=mgl(1-sinθ)sin2θ

通过观察发现,动能Ekb是关于θ的函数,而且是高次函数,所以用三角函数的方法有些困难.现在作函数的y-θ图像,如图2所示.

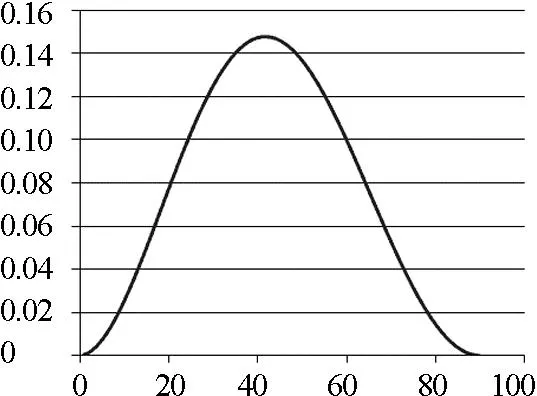
图2 y=(1-sin θ)sin αsin α函数图像

通过图线发现,函数的最大值在42°左右,并不是一个特殊值,这就需要用到费马定理.由于高中阶段对此介绍是通过例题出现的,在此简单介绍一下.

费马定理这样表述:若函数f(x)在x0点有导数,并且在x0的某邻域内恒有f(x)≤f(x0)[f(x)≥f(x0)]成立,则f′(x0)=0[1].费马定理的几何意义是:如果f(x)在x0的值不小于临近的函数值[或f(x0)不大于临近的函数值],只要在[x0,f(x0)]点曲线有切线,其切线必为水平.函数在x0处的切线水平,意味着函数在此处存在极值(函数的一阶导数等于零).

例题解法:设

y=mgl(1-sinθ)sin2θ

对其求导,有

y′=2mglsinθcosθ(2-3sinθ)

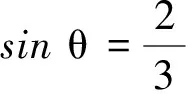
求导法不但可以解决三角函数的极值问题,也可以解决二次函数的极值问题.

【例2】(2017年高考全国Ⅱ卷第17题)如图3所示,半圆形光滑轨道固定在水平地面上,半圆的直径与地面垂直,一小物块以速度v从轨道下端滑入轨道,并从轨道上端水平飞出,小物块落地点到轨道下端的距离与轨道半径有关,此距离最大时,对应的轨道半径为(重力加速度为g)( )

图3 例2题图

分析:设小物块运动到最高点的速度为vt,半圆形光滑轨道半径为R,小物块由最低点运动到最高点,由机械能守恒定律,有

小物块从最高点飞出做平抛运动,则

联立解得

根式下面是一个关于R的二次函数,令

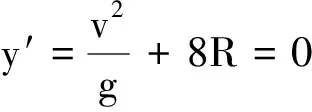
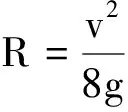
用这种方法比判别式方法求二次函数极值简单高效.

通过以上例题可以看出,在求极值问题上,求导法是难得的好方法.