分离变量法求解椭球星体的重力势增量

冉雪峰 谢祉锐

(重庆市育才中学校 重庆 400050)

1 引言

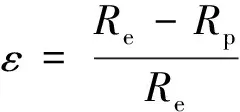
2 用分离变量法求解椭球星体的重力势增量

首先在椭球星体上建立如图1所示的直角坐标系,然后写出椭球的方程

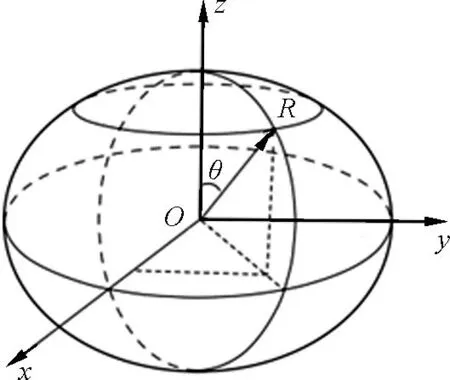
图1 直角坐标系下的椭球星体

由题设条件知:ε≪1,显然椭球关于z轴对称,且球外引力势U满足拉普拉斯方程

∇2U=0

(1)

轴对称情况下式(1)的通解为

(2)

取无穷远处势能U=0,可得an=0,因此,式(2)可简化为

由引力和势能的关系可得

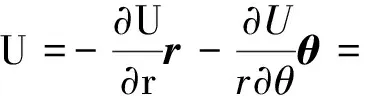
其中,Pn(cosθ)为勒让德函数.设

则

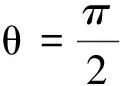
显然n为偶数时

从而得

n为奇数时

当且仅当2i=n+1时,该项不为零,故

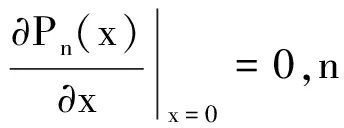
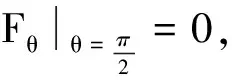
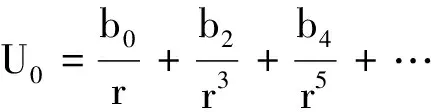
只保留首阶非零项得

U0=-2πGρ·

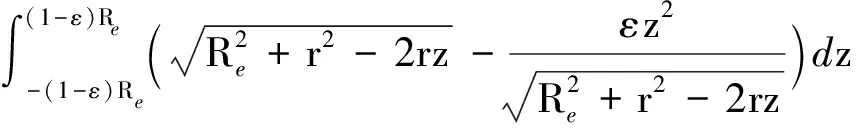
(3)

又ε≪1,故

(4)

将式(4)代入式(3)并由积分公式

可得

(5)

又

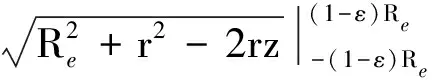
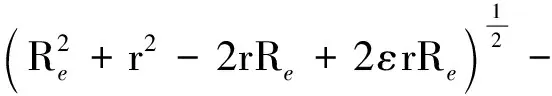
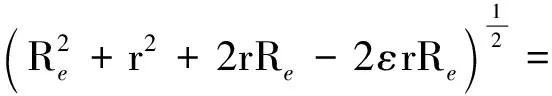
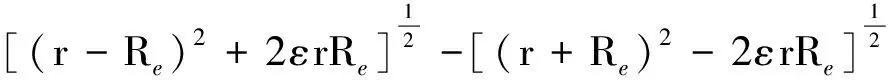
注意到ε≪1,对上式泰勒展开,并保留一阶小量得

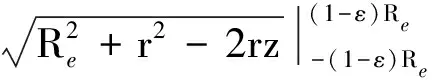
再将上式代入式(5)可得

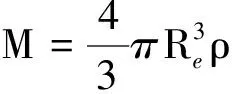
对比

易得

故

即得到重力势增量

3 结束语

本文用求解静电场电势分布的分离变量法解决了引力场中的引力势增量问题,一方面体现了引力场与静电场的相似性,另一方面也体现了知识和方法迁移的重要性.希望能给物理教学和竞赛辅导一些参考,以期和广大同仁共勉.