基于学科融合视角的“物理+”新情境问题——以地理中“潮汐现象”为例

何恩阳

(重庆市杨家坪中学 重庆 400050)

物理学是自然科学领域的一门基础学科,研究自然界物质的基本结构、相互作用和运动规律[1].随着高中学生物理知识结构的不断完善,学生逐步形成对自然现象进行观察和思考,建立模型,运用数学和物理知识进行科学推理和论证,最终解释自然现象的科学思维和探究能力.《高中地理课程标准2017版(2020修订)》核心素养中要求学生具有运用综合的观点认识地理环境的思维方式和能力[2].可见地理更偏向于对于自然现象的观察和描述,而物理更加侧重现象本质的分析和解释.地理现象为物理提供了激发学生探究兴趣的新情境,物理知识为解释地理现象提供了有力工具.学科融合,旨在充分承认不同学科对于学生能力培养侧重点差异的基础上,突破学科壁垒,使不同学科素养交叉融合,促进学生多学科知识的理解和应用,培养学生创新思维和应用知识解决实际问题的能力.

研究表明高中学生正处于具体运算阶段向形式运算阶段发展的关键时期[3],这意味着学生的思维方式需要在一个相对具体的物理情境中,基于对现象的观察思考,模型建构,从而总结出普遍的规律,逐步掌握从具体的物理现象抽象出物理本质的能力,最终学会运用公式符号去描述自然现象.通过学科融合,借助地理现象为物理知识的应用设立情境,提供知识应用的落脚点,帮助学生实现知识的内化和认知的发展,同时又进一步加深对于地理知识的深度理解,实现知识的整合,培养学生多学科维度的核心素养.

1 问题的提出

潮汐现象选自人民教育出版社高中地理教材必修一“海水的运动”一节,书中提到“潮汐是海水的一种周期性涨落现象,它的成因与月亮和太阳对地球的引力有关,一天中通常可以产生两次海水涨落”[4].关于两次涨落的成因,查阅大学地理教材《自然地理学》可以发现,在朝向和背离月球的洋面均出现上涨(图1),教材以地球不同位置处受到月球引力不同解释同一地点一天两次潮汐的原因,然而只给出了简单的文字描述没有给出定量分析[5].学生在已有的万有引力知识的基础上,会认为靠近月球的洋面受引力而洋面上涨,背离月球的洋面由于引力应该洋面回落,这与实际情况不符,容易引起学生的困惑.

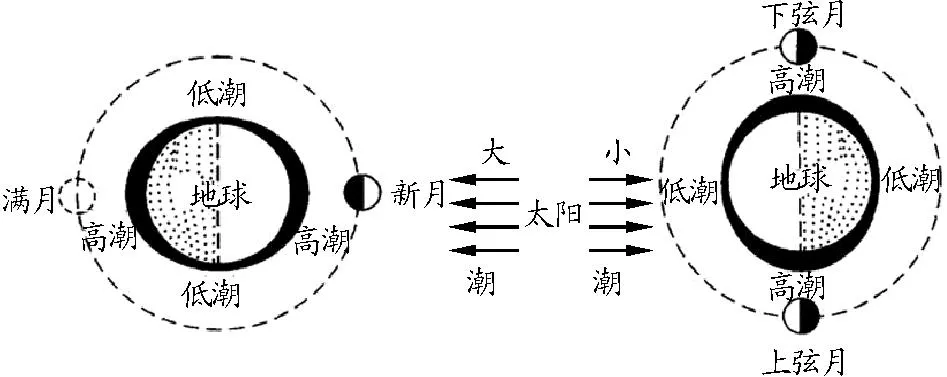
图1 《自然地理学》中对潮汐的描述

2 惯性力的引入

潮汐现象是海水相对地球运动形成的,要描述海水相对于地球的运动,首先要引入惯性力.在高中学生的已有认知体系中:力学规律只适用于惯性参考系,即以静止或匀速运动的物体为参考系.如苹果在匀速运动的列车中,以列车为参考系,苹果处于静止状态,此时苹果所受合力为零,如图2所示.而在匀加速运动的列车中,如果以列车为参考系,水平方向上苹果受到向右的摩擦力f,但是苹果却相对于列车处于静止状态,显然牛顿定律不再适用,需要引入与加速度反方向的惯性力f惯,如图3中虚线所示,才能确保牛顿定律在加速的列车参考系中成立.显然f惯与真实的作用力不同,没有施力物体的存在,而是为了在具有加速度的参考系中运用牛顿定律解决问题,而引入的假想力.可以发现,在以具有加速度的物体为参考系时(即非惯性系),牛顿定律不再适用,需引入惯性力,才能运用牛顿定律分析问题.

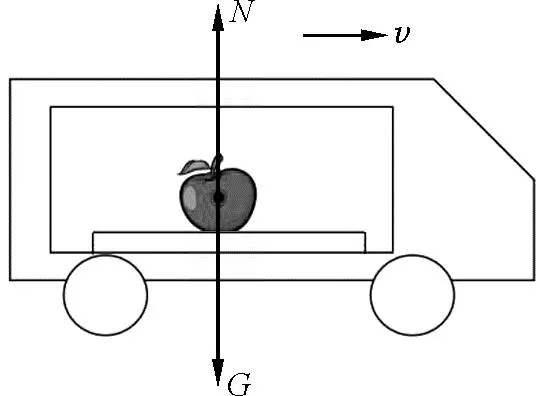
图2 匀速运动列车里的苹果

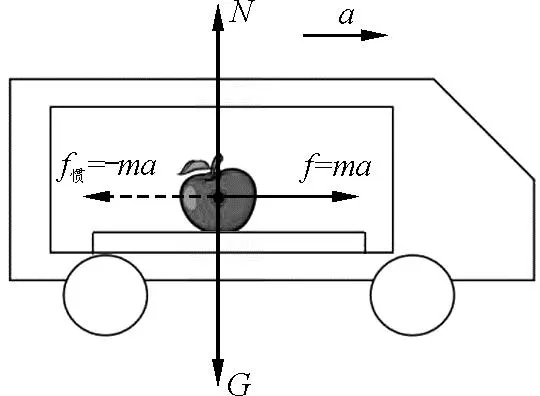
图3 匀加速运动列车中的苹果

在地月参考系中,地球由月球引力提供向心力,围绕地月共同质量中心做圆周运动;而要描述海水相对地球的运动,需要以地心为参考系,地球由于具有向心加速度而不再是惯性系,在转动的非惯性系中,需要如何引入惯性力,使得牛顿运动定律同样适用呢?以下面例子进行说明.

水平圆盘上的小球被一根轻绳系于圆心O点,随圆盘一起以角速度ω做匀速圆周运动,以地面为参考系时,小球受绳子的拉力T提供向心力,围绕O点做匀速圆周运动,如图4所示;而以旋转的圆盘为参考系时,小球相对圆盘静止,需要引入惯性离心力f惯才能与小球的运动状态吻合(图5).

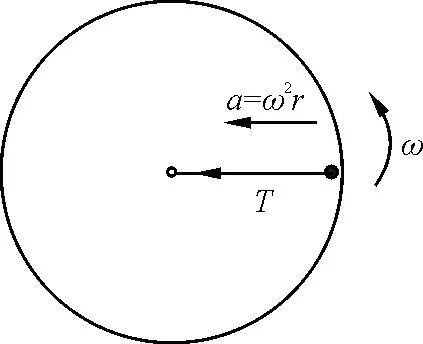
图4 以地面为参考系小球做匀速圆周运动

图5 以圆盘为参考系小球静止

3 问题的分析

3.1 建立物理模型 进行定量推导

由上可知,要在地心参考系中分析海水的受力情况,需要考虑地球因为绕地月共同质心做圆周运动而产生的惯性力.由于地球表面海洋分布并不均匀,且受到大陆阻隔,因此需要忽略次要因素,建立物理模型.首先,潮汐现象中月球的影响远大于太阳,因此,先只考虑月球对地球的影响;其次,忽略地球的地形变化,将地球视为质量分布均匀的球体;最后,地球表面约有71%的面积被海洋占据,因此忽略陆地的影响,认为海洋均匀覆盖于地球表面,并忽略洋流、气流、天气等复杂因素对潮汐的影响,物理模型如图6所示.

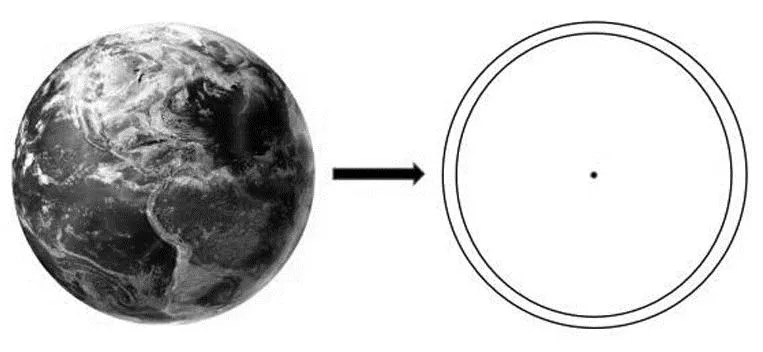
图6 物理模型建构

取地球表面一海水微元为研究对象,微元质量为m,地球球心O与月球球心O′的距离为r,微元与地球球心的距离为R,微元与月球球心的距离为r′(图7).研究海水相对于地球的运动,需以地心为参考系,地心参考系为非惯性系.首先求出地球的向心加速度,在惯性系中,地球整体受月球引力的动力学方程

(1)

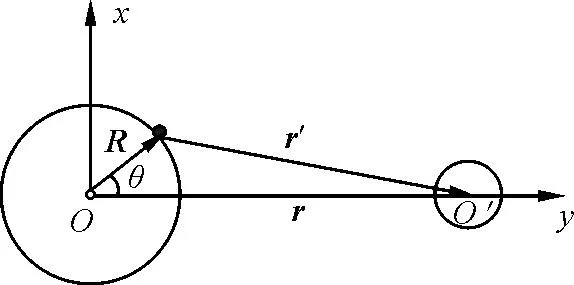
图7 地球、月球和海水微元之间的几何关系

此时海水微元受月球引力为

(2)

在地心参考系中海水微元的动力学方程为

fm+f惯+fe+f物质间的作用=ma

(3)

其中fe为地心对海水微元的引力,f物质间的作用为海水物质间的作用,这两种力与海水微元围绕地球转动对应的惯性离心力相互抵消,对潮汐现象无影响,剩余力即为潮汐力

f潮汐=fm+f惯

(4)

其中

f惯=-ma0

(5)

(6)

将式(2)、(5)、(6)代入式(4)得

(7)

其中r′、r、R构成矢量三角形,有

r=R+r′

(8)

利用余弦定理

r′2=r2+R2-2rRcosθ

(9)

利用r≫R可得

(10)

(11)

3.2 结果定量分析 明晰潮汐原因

将式(11)代入式(7),并写出分量形式

(12)

(13)

分别取θ为0°(距月球最近点)、90°、180°(距月球最远点)、270° 4个特殊位置,如图8所示.

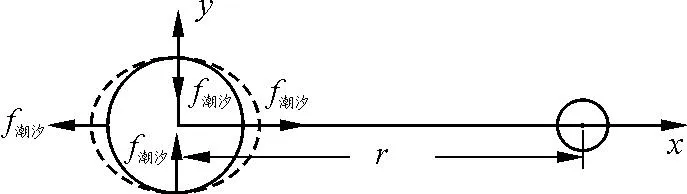
图8 潮汐力作用下地球表面海水分布

可以发现距离月球最近和最远点海水所受潮汐力方向均背离地球球心,两位置的洋面上涨;沿y轴两点海水所受潮汐力方向均指向地球球心,两位置的洋面回落.由于地球自转,地球上某点海水一天会距离月球最近和最远各一次,因此会出现两次海水涨落现象.

因太阳引力引起的地球海洋的潮汐现象同理,只需将式(7)、(12)、(13)中的月球质量Mm更换为太阳质量Ms,将月地距离r更换为日地距离re,s即可,将太阳的潮汐力和月球的潮汐力进行比较

可以看出潮汐现象月球对地球的作用大于太阳对地球的作用.这解释了图1中,当太阳、地球、月球三者共线时,太阳和月球的引潮力叠加,会出现大潮(潮的浪更高);当日地连线和月地连线垂直时,太阳和月球的引潮力部分抵消,会出现小潮(潮的浪更低),但潮的位置始终在地月连线上靠近和远离月球的位置.

3.3 原理定性解释 形成物理观念

“物理观念”是基于物理学视角关于物质、运动、相互作用和能量的基本认识;是物理概念在头脑中的提炼与升华;是从物理视角解释自然现象和实际问题的基础[1].通过对定量计算结果的分析,把握其中的物理原理和规律,能够帮助学生对物理知识和规律进行内化,最终建构学生自己的认知体系.

通过式(4)、(7)可知,在地心参考系下,地球表面的海水始终受到惯性离心力f惯和月球对海水的引力fm作用,任意位置处海水所受惯性离心力f惯相同,而受到月球对海水的引力fm由于不同位置处微元和月球的距离r′不同而不同.其中距离月球最近处的海水微元,所受月球引力较大,因此f惯fm远使海水所受合力(即潮汐力f潮汐)与惯性离心力f惯方向相同,潮汐力指向背离月球方向,如图9所示.

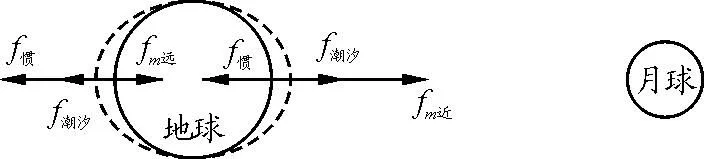
图9 地心参考系下距离月球最近和最远处的海水受力分析

由式(5)可知,惯性离心力f惯中的向心加速度a0是由于月球对整个地球(可视为地球质量集中于球心)的引力产生的,所以潮汐现象实质是地球表面不同位置处海水微元到月球球心距离和地球球心到月球球心距离不同,使得不同位置海水微元所受的f惯和fm不同引起的,可以发现在地球球心处取一微元,微元所受f惯和fm刚好等大反向,合力为零,没有引潮力作用.因此引潮力的大小核心影响因素在于,地球不同位置处微元所受月球引力与微元所受惯性离心力的矢量和.由于月球距离地球较近,使得地球不同位置处所受引力变化较大,因此f惯和fm差别较大,月球引发的潮汐现象更加明显.由于太阳和地球的距离较远,太阳对地球不同位置处引力变化较小,因此f惯和fm的差别较小,潮汐力不明显.这也解释了为什么明明太阳对地球的引力远大于月球对地球的引力,然而潮汐现象主要由月球引起.

4 总结

通过地理教材的潮汐内容中的“反直觉”现象,激发学生的认知驱动力,通过建构合理的认知过程,补充在非惯性系中惯性力等前置知识,引导学生在“最近发展区”内,基于已有的知识,建立模型,进行科学推理和论证,列式分析,给出潮汐现象的定量分析公式.同时基于公式思考其中所隐含的科学本质,促进学生对于运动和相互作用观念的逐渐深化.引导学生运用物理观点认识地理现象的本质,通过物理角度的思考和分析,进一步加深对于地理知识的理解,帮助学生认识到科学的统一性,学会用学科融合视角看待科学问题,最终实现多学科素养的提升.