巧求椭圆柱面的转动惯量*

黎 磊 万慧军 勾庆东

(井冈山大学数理学院 江西 吉安 343009)

转动惯量是物理学乃至整个自然科学的一个重要概念,它反映了物体转动下的惯性,转动惯量越大的物体角速度越难被改变.作为转动定理中的一个重要物理量,转动惯量贯穿在整个转动力学中,掌握转动惯量的多种计算方法是学好转动动力学的前提.众多大学物理教材以及教学参考书中会给出较为简单的刚体模型对相应转轴的转动惯量计算公式,如匀质的圆环、圆盘、圆柱体、圆柱面、球、球面等,不过基本都是在直角坐标系下利用转动惯量的定义直接积分求得.针对不同类型的刚体模型,往往可以有不同的转动惯量计算方法和技巧,选取合适的方法可以简化计算,比如:文献[1]利用三角形的顶点坐标与边长的关系,直接推导出任意的匀质三角形框线绕其质心轴旋转的转动惯量.文献[2]应用量纲分析法,递推出了几类分形物体的转动惯量.文献[3]用广义柱面坐标变换计算了椭圆柱体绕对称轴旋转的转动惯量.文献[4]用质量投影法计算了均质椭圆柱面刚体对中心对称轴的转动惯量.文献[5]在极坐标下计算了匀质椭圆环和椭圆盘对过焦点和过中心的竖直转轴的转动惯量.

本研究针对椭圆柱面模型,利用极坐标在表示质元到转轴距离上的优势,采用以椭圆中心为极点的极坐标方程并结合平行轴定理,计算了椭圆柱面绕3个中心对称轴旋转的转动惯量.本方法另辟蹊径,不需要给出曲面的面积微元表达式,对于初学者更容易理解,本研究内容推导过程详细,思路清晰,不管是对极坐标的应用教学还是对转动惯量的求解教学都具有启发意义.

1 椭圆柱面的转动惯量

如图1所示,在椭圆柱面模型中建立直角坐标系Oxyz,原点O选在椭圆柱面中心横截面的中心,x轴沿着横截面椭圆的长轴方向,y轴沿着横截面椭圆的短轴方向,z轴沿着椭圆柱面的高度方向.椭圆柱面的质量为m,高度为L,横截面椭圆的长半轴为a,短半轴为b,离心率为e.采用微元法,在椭圆柱面上选取宽度为dz的薄椭圆环作为微元,椭圆环到Ox、Oy转轴的距离为z.我们首先计算椭圆环微元绕Ox、Oy、Oz轴转动的转动惯量.

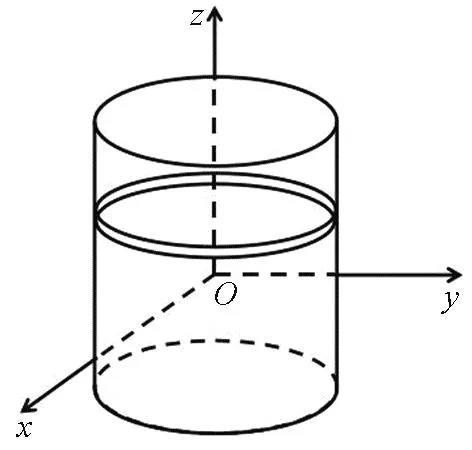
图1 椭圆柱面示意图

如图2所示,以中心为极坐标原点的椭圆的极坐标方程可以表示为

(1)

图2 椭圆环微元

椭圆环的弧长微分在极坐标下可表示为

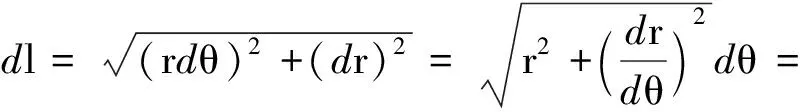
(2)

对式(2)进行化简积分,得到椭圆环的长度表达式为

(3)

根据转动惯量的计算公式并结合平行轴定理,可以将椭圆环绕Ox、Oy、Oz轴转动的转动惯量分别写为

(4)

(5)

(6)

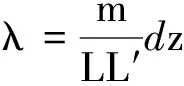
对式(4)积分,可求出椭圆柱面绕Ox轴转动的转动惯量为

(7)

对式(5)积分,得到椭圆柱面绕Oy轴转动的转动惯量为

(8)

同理,对式(6)积分,得到椭圆柱面绕Oz轴转动的转动惯量为

(9)

2 讨论与数值计算

我们讨论一种特殊情况,当椭圆的离心率e=0时,椭圆柱面转化为圆柱面,此时椭圆的长短半轴相等,有a=b=R(圆半径),椭圆周长L′=2πR.将这些代入式(7)、(8)、(9),计算可得

此即圆柱面绕相应对称轴旋转的转动惯量表达式.

因为椭圆柱面的转动惯量不能用只包含初等函数的解析表达式写出来,所以我们对式(7)、(8)、(9)进行数值计算.假设m= 12 kg、L= 4 m,图3、4、5分别给出了Jx、Jy、Jz对横截面椭圆长短半轴a、b的依赖关系曲面.特别地,当a=b=R=3 m时,如图3、4、5所示,数值结果表明Jx=70 kg·m2,Jy= 70 kg·m2,Jz= 108 kg·m2,这和圆柱面对相应转轴的转动惯量的理论公式结果

图3 椭圆柱面绕Ox轴旋转的转动惯量Jx

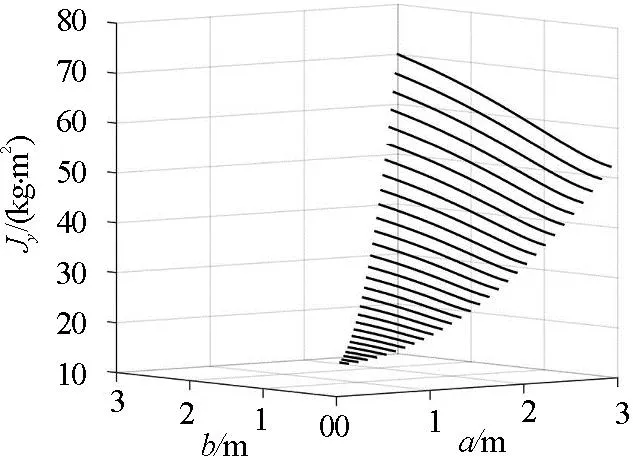
图4 椭圆柱面绕Oy轴旋转的转动惯量Jy

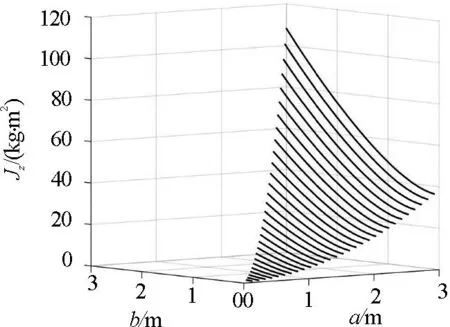
图5 椭圆柱面绕Oz轴旋转的转动惯量Jz

Jz=mR2=108 kg·m2

一致.

3 总结

本文在极坐标下结合平行轴定理巧妙地求解了匀质椭圆柱面分别绕Ox、Oy、Oz3个中心对称轴旋转的转动惯量,并对结果进行了讨论和数值计算.本研究内容不仅可以用于大学物理教学中对转动惯量相关计算的扩充讲解,也可以在极坐标相关应用的课堂教学中发挥作用,加深学生对转动惯量和极坐标这两个知识点的认识.另外,本文中的计算方法也可以用于椭圆柱体、椭球体、椭球面等模型的转动惯量计算,作为课本上没有涉及的扩充解法.这种基于新的求解思路的教学可以激发学生对大学物理理论知识的探究兴趣,培养学生的创新性思维能力.