论匀速运动有限长带电直导线的位移电流

吴冰驰

(广东工业大学轻工化工学院 广东 广州 510000)

麦克斯韦假设存在位移电流,从而将安培环路定理推广到全电流定律,从表达式上很难看出传导电流和位移电流之间的密切联系,通过求解匀速运动有限长带电直导线的位移电流,发现了传导电流和位移电流之间的密切关系.

1 匀速运动有限长均匀带电直导线的位移电流

真空状态,在空间直角坐标系中,带正电荷直导线两端点为A和B,长度为l,电荷线密度为λ,导线和x轴重叠,沿x轴正方向以速率v做匀速直线运动,t时刻A点位于x轴上的坐标点为(vt,0,0),t时刻B点位于x轴上的坐标点为(vt+l,0,0).r1=(x-vt)i+yj+zk是A点到场点P(x,y,z)的矢径,矢径r1与x轴之间的夹角为θ1,r2=(x-vt-l)i+yj+zk是B点到场点P(x,y,z)的矢径,矢径r2与x轴之间的夹角为θ2,过P(x,y,z)点作x轴的垂线,垂线和x轴交点为D,R为P(x,y,z)到x轴的距离.以D点为圆心,R为半径作圆,圆周长为C,圆面积为S,圆平面和x轴垂直,作圆是为了求通过圆面积S的位移电流和环绕圆周C的磁场环路积分,如图1所示.

图1 带电导线AB的电磁场

带电运动导线每一无穷小段dl相当于点电荷,匀速运动点电荷电磁场方程[1]

(1)

(2)

其中,q=λdξ,带电运动导线电场积分如下

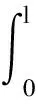
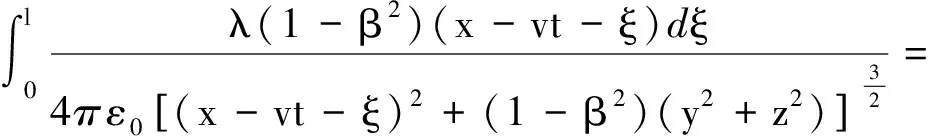
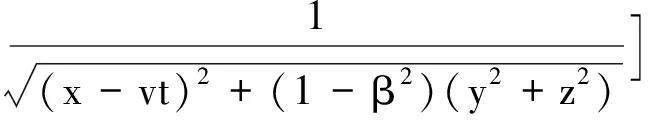
(3)

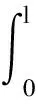
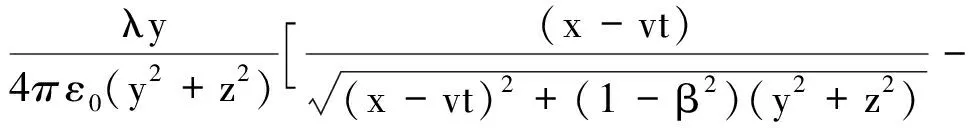
(4)

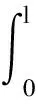
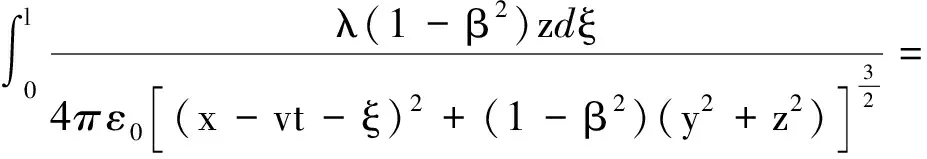
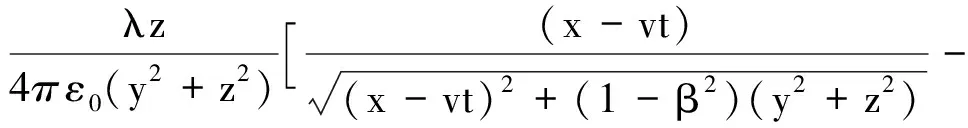
(5)

带电运动导线上每一无穷小段dl的磁场方程满足式(2),所有无穷小段dl的磁场积分也满足式(2),其中v=(v,0,0),带电运动导线磁场分解为

Bx=0

(6)

(7)

(8)

已知By、Bz,对环绕圆周C的磁场做环路积分,得到

∮B·dC=∮(Bydy+Bzdz)=

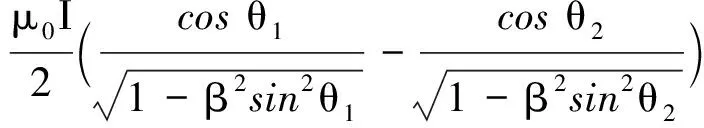
(9)

讨论:

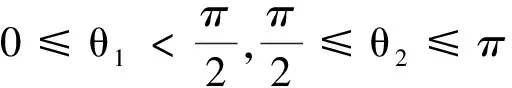
(10)

此处的位移电流和传导电流是正比例关系,位移电流和传导电流方向相反.

将式(10)乘以μ0,移项得

(11)

比较式(9)和式(11)得到

(12)

式(12)为全电流定律表达式.

(13)

此处位移电流和传导电流方向相同,位移电流和运动导线产生的传导电流是正比例关系.

式(9)中当θ1=0,θ2=π时,有

∮B·dC=μ0I

(14)

式(14)为无限长运动带电导线的全电流定律,等价于闭合电路稳恒电流的安培环路定理.

2 结束语

通过研究匀速运动均匀带电导线产生的位移电流,得出结论:传导电流穿过截面时,位移电流和传导电流方向相反.传导电流未穿过截面时,位移电流和运动导线产生的传导电流方向相同.传导电流和位移电流关系密切,传导电流和位移电流是正比关系.并且在求解位移电流时,导出了麦斯韦方程组的全电流定律.匀速运动均匀有限长带电导线形成的电流不随时间变化,所以是稳恒电流,但电流不闭合.