基于模糊三支区间集半概念知识提取方法研究
毛 华, 牛振华, 马经泽, 张植明, 杨兰珍
(1.河北大学 数学与信息科学学院 河北 保定 071002; 2.河北省机器学习与计算机智能重点实验室 河北 保定 071002)
0 引言
Yao[1]提出的三支决策模型,是对二支决策的一个推广,是在原有的接受和拒绝二支决策的模型上添加了不承诺这一延迟决策[2-3]。概念格是一种基于形式背景进行数据处理的数学工具[4]。形式背景是其数据的载体,概念是其知识的表达形式,整个知识构成格结构,为形式概念分析的核心内容,广泛应用于人工智能和知识提取等[5-7]领域。在实际问题中,有些知识只需要考虑对象所拥有的属性或者属性所具有的对象。因此,作为形式概念分析的提升,Vormbrock等[8]提出经典半概念,并且建立了经典半概念理论。
因三支决策更符合人类认知,Ren等[9]将三支决策与概念格结合,提出了三支概念格的属性约简;Mao等[10-11]将三支决策思想与经典半概念理论相结合,提出了两种形式的半概念和三支粗糙半概念;康凯等[12]提出了基于三支聚类的协同过滤推荐方法。另外,在实际问题中,知识载体也经常具有不确定性关系,模糊形式背景具有描述这种不确定性和确定性的二元关系。毛华等[13]将三支半概念和模糊集理论相结合,提出了面向对象的模糊三支半概念。
在许多实际问题中,有些知识往往不能被精确定义,假设一个实体是否是概念的实例仅有两种可能,即是或非,由于信息不完全,并不能对所有实体都作出这种明确的判断,这个概念称为部分已知的。为了描述这种部分已知概念,Yao[14]提出了有限域上一种新的集合概念:区间集。区间集是由一对上界和下界所表示的闭区间,下界表示所有确定属于该概念的实体,上界表示所有可能属于该概念的实体。钱婷等[15]介绍了完备形式背景上区间集概念格的构造方法,刘营营等[16]提出了三支区间集概念格。
目前对于区间集概念格的研究中,仍然束缚在经典概念格和二支决策的理论中。为解决不确定二元关系的实际问题,模糊形式背景具有描述知识载体不确定性的二元关系,三支决策是知识提取与发现的工具,本文将区间集概念格与三支决策、经典半概念和模糊集结合,提出了模糊形式背景下的面向属性的三支区间集半概念,证明其格性质,并且给出了模糊三支区间集半概念算法,通过实例验证了算法的有效性。由于研究目的是解决实际问题,而实际情况均为有限,故本文讨论的内容均为有限。
1 预备知识
本节首先介绍了经典半概念和模糊AE-半概念,接着介绍了三支区间集概念格,更详细内容见参考文献[8,14,16-17]。
定义1[8]给定一个形式背景K=(U,V,R),非空集合U为对象集,非空集合V为属性集,R为U与合V之间的一个二元关系,若x∈U,a∈V,对象x具有属性a当且仅当(x,a)∈R或xRa。
算子*:2V→2U定义为
A*={x|x∈U,∀a∈V,aRx},(A∈2V)。
对于X∈U,A∈V,若A*=X,则称(X,A)为∪半概念,X为(X,A)的外延,A为(X,A)的内涵。
定义2[17]设K~=(U,V,R~)是一个模糊形式背景,U为所有对象构成的集合,V为所有属性构成的集合,R~为一个定义在U×V上的模糊集。若(x,a)∈R~,μ(x,a)称为对象x关于属性a的隶属度,则有0≤μ(x,a)≤1。
定义3[17]设K~=(U,V,R~)是一个模糊形式背景,给定一个阈值ε,X⊆U,A⊆V,则定义模糊三支算子◁:2V→2U×2U,
定义模糊正算子*ε:2V→2U为
A*ε={x|x∈U,∀a∈V,μ(x,a)≥ε},A∈2V。
对偶得到模糊三支算子▷:2U→2V×2V,
其中:X*ε={a|a∈V,∀x∈U,μ(x,a)≥ε};

引理1[12]设K~=(U,V,R~)是一个模糊形式背景,给定一个阈值ε,对于任意的属性子集A,B⊆V,则有A⊆B⟹A◁⊇B◁。
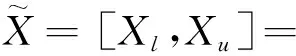


4)X=[U,U]-[Xl,Xu];
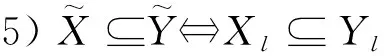
2 模糊AE-区间集半概念
本节首先引入模糊AE-区间集半算子,接着定义模糊AE-区间集半概念,其次讨论模糊AE-区间集半概念的格结构,并在此基础上给出寻找模糊AE-区间集半概念全体的算法。
2.1 定义
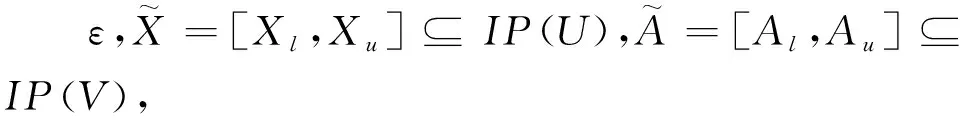
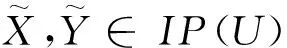
用实例解释模糊AE-区间集半概念。
例1对大学某班的三名文娱委员红红、明明、聪聪进行调查,各自对三项活动的擅长程度进行打分(满分为1分),得到一个信息调查表,见表1。
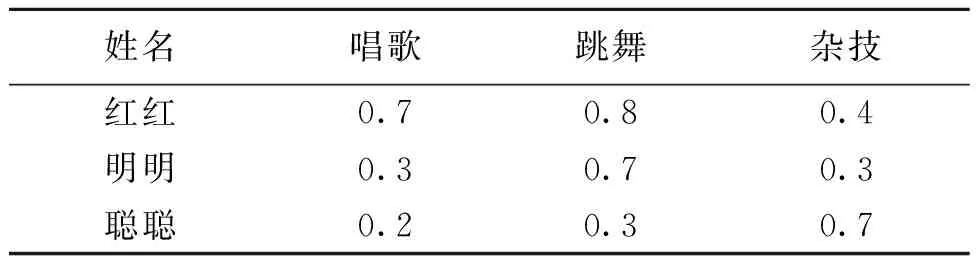
表1 信息调查表Table 1 Schedule of information survey
现在设K=(U,V,R~)是一个模糊形式背景,U={1,2,3}代表对象集,其中:1代表红红;2代表明明;3代表聪聪。V={a,b,c}代表属性集,其中:a代表是否擅长唱歌;b代表是否擅长跳舞;c代表是否擅长杂技。R~表示对象集和属性集之间的二元关系,取阈值ε=0.6,当μ(x,a)≥0.6时,可认为该同学擅长某项活动,那么表1的形式背景如表2所示。
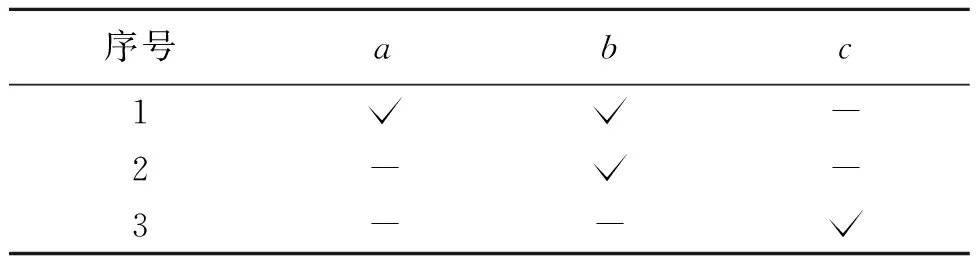
表2 形式背景K=(U,V,R~)Table 2 Formal context K=(U,V,R~)

由此反映出1号同学擅长唱歌、跳舞,可以推荐1号同学去参加学校组织的歌唱活动,2号同学只擅长唱歌,当1号同学有什么紧急情况不能去参加学校组织的歌唱活动时,2号同学可作为备选人员参加,3号同学既不擅长唱歌也不擅长跳舞,那么这次活动不推荐3号同学。由定义8可知(([1,12],[3,3]),[a,ab])是模糊AE-区间集半概念。

2.2 性质
形式概念分析的核心是格结构,格是知识提取的依据,接下来讨论模糊AE-区间集半概念的格结构。为此,由格的定义,先讨论它的偏序性质。
定理1设K~=(U,V,R~)是一个模糊形式背景,则(FISSCLAE,≤)在定义9给出的关系中构成一个偏序集。
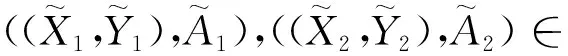

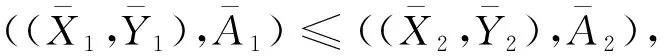
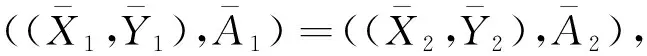

得≤为偏序关系,(FISSCLAE,≤)是偏序集。

(FISSCLAE,∨,∧)是一个完备格,称之为模糊AE-区间集半概念格。
证明(FISSCLAE,∨,∧)是一个格。

综上可证(FISSCLAE,∨,∧)是一个格。
接下来对模糊半概念(X,A)、模糊AE-半概念((M,N),B)和模糊AE-区间集半概念(([Ml,Mu],[Nl,Nu]),[Bl,Bu])进行对比。
从形式上进行对比。
1) 模糊半概念(X,A)为二维数据;模糊AE-半概念((M,N),B)为三维数据;模糊AE-区间集半概念(([Ml,Mu],[Nl,Nu]),[Bl,Bu])为三维区间集数据。
2) 对于模糊AE-区间集半概念(([Ml,Mu],[Nl,Nu]),[Bl,Bu]),Ml=Mu,Nl=Nu,Bl=Bu时为模糊AE-半概念。
3) 模糊半概念(X,A)仅考虑了属性拥有的对象,模糊AE-区间集半概念(([Ml,Mu],[Nl,Nu]),[Bl,Bu])不仅考虑了属性区间集共同拥有的对象区间集,也考虑了属性区间集共同不拥有的对象区间集。因此模糊AE-区间集半概念的应用范围更广泛。
从结构上进行对比。
1) 模糊半概念(X,A)、模糊AE-半概念((M,N),B)、模糊AE-区间集半概念(([Ml,Mu],[Nl,Nu]),[Bl,Bu])都可以构成格。
2) 每一个概念可以看成一个知识,通过建立不同的泛化-例化关系,构成各自的格,进而进行知识提取。
2.3 算法
接下来根据已知模糊形式背景,给出寻找模糊AE-区间集半概念全体的算法。
算法1寻找模糊AE-区间集半概念全体
输入:K~=(U,V,R~),阈值ε。
输出:FISSCLAE。
1: LETFISSCLAE=∅
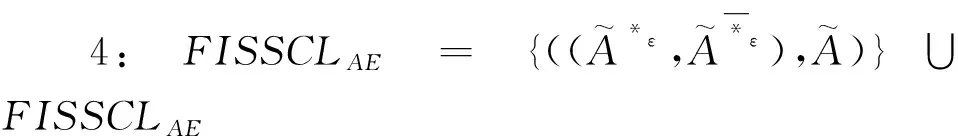
5: END IF
6: ENF FOR
7: GENERATEFISSCLAE
现分析算法1 的时间复杂度,步骤2的复杂度为O(2|V|×2|V|)=O(2(2×|V|)),步骤3的复杂度为O(2×|U|),则算法1的复杂度为O(2(2×|V|)+2×|U|)。
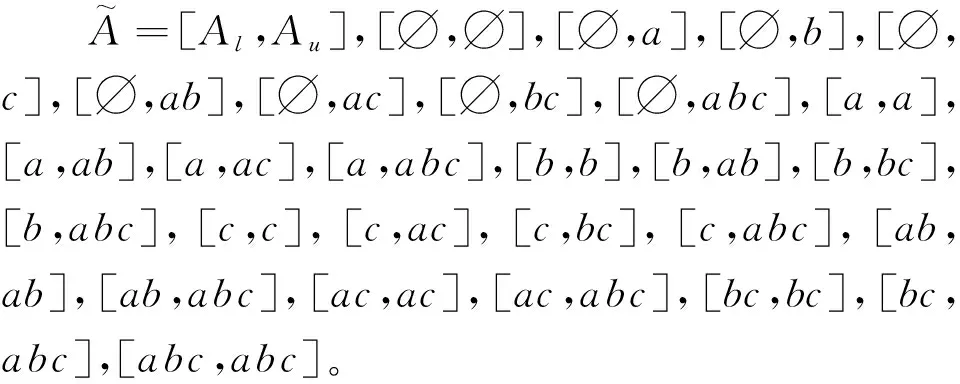

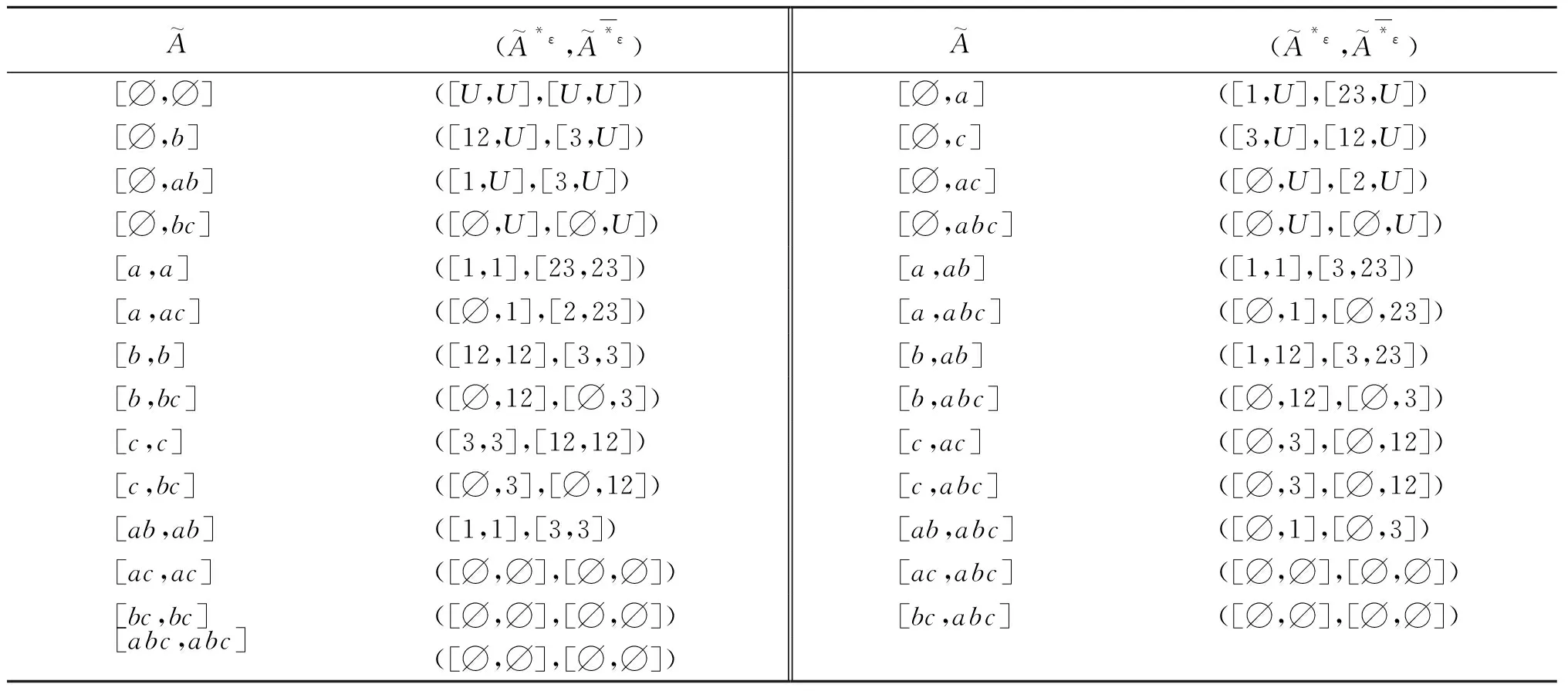
表3 模糊AE-区间集半算子Table 3 Fuzzy AE-interval-set semioperator

根据定理2可以得到模糊AE-区间集半概念格,如图1所示。为方便起见,在模糊AE-区间集半概念格的图中只列出模糊AE-区间集半概念格的内涵。该例子说明了算法1的有效性。

图1 模糊AE-区间集半概念格Figure 1 Fuzzy AE-interval-set semiconcept lattice
3 模糊OE-区间集半概念
由于模糊AE-区间集半概念与模糊OE-区间集半概念具有对偶性,从而对偶地,可得到有关模糊OE-区间集半概念性质的证明。
定义10设K~=(U,V,R~)是一个模糊形式背景,给定一个阈值


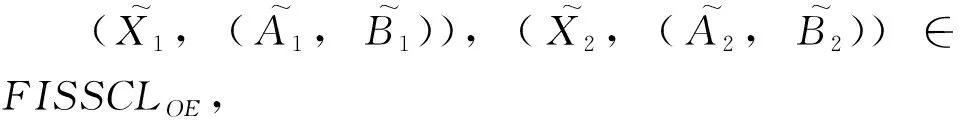
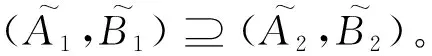
定理3设K~=(U,V,R~)是一个模糊形式背景,则(FISSCLOE,≤)在定义12给出的关系中构成一个偏序集。
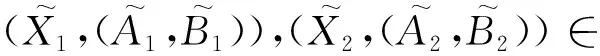
(FISSCLOE,∨,∧)是一个完备格,称之为模糊OE-区间集半概念格。
算法2寻找模糊OE-区间集半概念全体
输入:K~=(U,V,R~),阈值ε。
输出:FISSCLOE。
LETFISSCLOE=∅

END IF
ENF FOR
GENERATEFISSCLOE
4 结论
考虑实际问题,有些知识是在模糊形式背景下提取的,作为区间集概念格的拓广,本文将区间集与三支决策和经典半概念和模糊集理论结合起来,提出两种形式的模糊三支区间集半概念(模糊AE-区间集半概念和模糊OE-区间集半概念),使知识提取的应用更为广泛。本文是在完备形式背景下研究的,不完备形式背景下的三支区间集半概念和经典形式背景下的三支区间集半概念也值得进行探究。

