基于集覆盖理论的覆盖信息系统属性约简方法
徐 晔, 许晴媛, 李进金
(1.闽南师范大学 计算机学院 福建 漳州 363000; 2.闽南师范大学 数据科学与智能应用福建省 高校重点实验室 福建 漳州 363000; 3.闽南师范大学 数学与统计学院 福建 漳州 363000; 4.闽南师范大学 福建省粒计算及其应用重点实验室 福建 漳州 363000)
0 引言
粗糙集理论是用于处理各种不确定性信息的有效工具[1-2],已成功应用在机器学习、模式识别等人工智能领域。然而,现实中的各类信息系统具有不同类型的属性,如数值属性、集值属性、缺失属性等,经典粗糙集理论在处理这些数据时具有局限性。因此,人们提出许多方法去推广经典粗糙集理论,例如多粒度近似空间的模糊粗糙集[3]、多粒度决策粗糙集[4]、覆盖粗糙集[5]等。其中,覆盖粗糙集是一个比较重要的推广方向。
覆盖信息系统属性约简问题是覆盖粗糙集方向的重要研究课题,探索覆盖信息系统的属性约简方法是当前的研究热点[6-10]。其中,文献[6]通过产生相同上、下近似最小覆盖的方法得到属性约简,为覆盖信息系统属性约简提供了一种有效的方法;文献[7]利用区分矩阵求解覆盖信息系统的属性约简;文献[8]在文献[6]的基础上利用信息熵刻画了覆盖约简的粗糙性。
集覆盖问题是一个优化问题,已广泛应用于航空人员调度、运输车辆路线安排、服务位置、制造作业分配、操作人员选择等领域。解决集覆盖问题的经典算法有人工蜂群算法[11]、DNA计算方法[12]、贪心算法[13]及近似算法[14]等。改进集覆盖问题的经典算法是当前的研究热点[15-17],例如文献[16]针对unicost集覆盖问题,提出一种改进的基于配置检查的算法。近年来,出现了集覆盖问题与粗糙集属性约简问题的交叉研究。其中,文献[18]提出利用集覆盖问题解决传统粗糙集属性约简问题;文献[19-20]提出利用集覆盖问题解决粗糙集扩展领域的属性约简问题。反过来,利用粗糙集理论来解决集覆盖问题的方法也相继被提出[21-24]。
本文提出一种把覆盖信息系统的属性约简问题转化为集覆盖问题的方法,并应用集覆盖理论来研究覆盖信息系统的属性约简问题。通过构造覆盖信息系统的相关矩阵诱导出覆盖信息系统的集覆盖模型,进而建立集覆盖问题与覆盖信息系统属性约简问题之间的联系,得出集覆盖模型的一个极小覆盖恰是原覆盖信息系统的一个属性约简集,从而可以借助高效的集覆盖理论来求解覆盖信息系统的属性约简问题。集覆盖启发式算法(set covering heuristic algorithm,SCHA)[25]在解决集覆盖问题上具有较高的精度与较好的性能,本文给出了基于SCHA求解覆盖信息系统属性约简的算法,并通过一个实例验证了所提方法的可行性和有效性。本文工作丰富了集覆盖理论与覆盖粗糙集理论的交叉研究,为覆盖信息系统的属性约简问题带来了新的思路与方法,同时拓展了集覆盖理论的应用领域。
1 基本概念
1.1 集覆盖问题
定义1设E={xq:1≤q≤y}是一个非空有限对象集合,S={Sw:1≤w≤r}是E的若干非空子集构成的集族。若∪S=E,则称S为E的一个集覆盖,称(E,S)为一个集覆盖模型。集覆盖问题在于求解S的一个非空子集S′,使得∪S′=E,且S′的任意真子集都不是E的覆盖。S′也称为E关于覆盖S的一个极小覆盖。
1.2 覆盖信息系统及其属性约简问题
定义2[26]给定一个论域U={xi:1≤i≤n},设C={Xk:Xk⊆U,1≤k≤t}。如果C中的所有子集都不为空,且∪C=U,则称C是U的一个覆盖。
定义3[26]设U={xi:1≤i≤n},C={Xk:1≤k≤t}是U的一个覆盖。∀xi∈U,记(xi)C=∩{Xk:Xk∈C,xi∈Xk},记Cov(C)={(xi)C:xi∈U},则Cov(C)也是U的一个覆盖,称Cov(C)为C诱导的覆盖。
定义4[26]设ζ={Cj:1≤j≤m}是论域U上的一族覆盖。对于任意的x∈U,记Δζ(x)=∩{(x)Cj:1≤j≤m},称Cov(ζ)={Δζ(x):x∈U}为ζ诱导的覆盖,称(U,ζ)为一个覆盖信息系统。设β⊆ζ,若对于任意的x∈U,有Δβ(x)⊆Δζ(x),则记Cov(β)≤Cov(ζ)。
定义5给定一个论域U={xi:1≤i≤n},设ζ={Cj:1≤j≤m}是论域U上的一族覆盖,定义U上的一个关系R={(xo,xp):xo∈Δζ(xp),xo∈U,xp∈U}。
定义6设ζ={Cj:1≤j≤m}是论域U上的一族覆盖,(U,ζ)是一个覆盖信息系统。对于任意的P⊆ζ,若Cov(P)≤Cov(ζ),则称P是(U,ζ)的一个覆盖协调集。若对于∀Cj∈P,Cov(P-{Cj})≤Cov(ζ)均不成立,则称P是(U,ζ)的一个覆盖约简集。
定义7设(U,ζ)是一个覆盖信息系统,若P={Pz:1≤z≤e}是(U,ζ)的所有约简集,则称Core(ζ)={P1∩P2∩…∩Pn}是(U,ζ)的核属性集。
2 覆盖信息系统的集覆盖模型
在本节中首先定义关于覆盖信息系统(U,ζ)的相关矩阵M,然后通过矩阵M诱导出关于覆盖信息系统(U,ζ)的集覆盖模型(U′,S′),并给出覆盖信息系统(U,ζ)与其诱导的集覆盖模型(U′,S′)之间的一些联系。
定义8设(U,ζ)是一个覆盖信息系统,U={xi:1≤i≤n},ζ={Cj:1≤j≤m},R={(xo,xp):xo∈Δζ(xp),xo∈U,xp∈U}。令U′={(xp,xo):(xp,xo)∉R,xp∈U,xo∈U},记U′={ui:1≤i≤n2-|R|}。定义一个f行m列的矩阵M,其中f=n2-|R|,M中的行由U′中元素构成,M中的列由ζ中元素构成,M的第i行第j列元素Mij取值为
称M为覆盖信息系统(U,ζ)的相关矩阵。
注: 因为U={xi:1≤i≤n}中有n个元素,U′中的元素为(xp,xo)的形式,所以U′中元素个数最多为n2个。由于U′={(xp,xo):(xp,xo)∉R,xp∈U,xo∈U},故U′中元素个数等于f=n2-|R|。
定理1设(U,ζ)是一个覆盖信息系统,M为(U,ζ)的相关矩阵,M中不存在所有列的值全为0的行。
证明设存在第i行所有列的值全为0,ui=(xp,xo)∈U′,则对于∀Cj∈ζ,Mij=0,有xo∈(xp)Cj。根据Δζ(x)=∩{(x)Cj:1≤j≤m},可得xo∈Δζ(xp)。根据定义5,ui=(xp,xo)∈R,与定义8中U′={(xp,xo):(xp,xo)∉R,xp∈U,xo∈U}矛盾。因此,矩阵M中不存在所有列的值全为0的行。
定理2设(U,ζ)是一个覆盖信息系统,M为(U,ζ)的相关矩阵。令ui=(xp,xo)∈U′,若Mij=1,则Cj可以区分对象对ui=(xp,xo)∈U′。
证明令ui=(xp,xo)∈U′,若存在Mij=1,则存在Cj∈ζ使得xo∉(xp)Cj,故xo∉Δζ(xp)。因此,Cj可以区分对象对ui=(xp,xo)∈U′。
推论1设(U,ζ)是一个覆盖信息系统,U′={(xp,xo):(xp,xo)∉R,xp∈U,xo∈U}={ui:1≤i≤n2-|R|}。对于U′中的任意一个元素ui=(xp,xo),都存在一个覆盖Cj使得xo∉(xp)Cj。
证明由定理1与定理2容易得证。
接下来,给出一个由覆盖信息系统诱导的区分集合的定义。
定义9设(U,ζ)是一个覆盖信息系统,U′={ui:1≤i≤n2-|R|},令SCj=∪{ui:Mij=1,ui∈U′},则SCj为U′中所有能被Cj区分的ui构成的集合,称SCj为Cj诱导的区分集合。

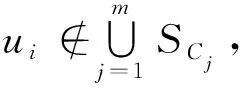
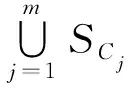
定理4设(U,ζ)是一个覆盖信息系统,ζ={Cj:1≤j≤m},U′={(xp,xo):(xp,xo)∉R,xp∈U,xo∈U},S′={SCj:1≤j≤m},(U′,S′)为(U,ζ)诱导的集覆盖模型。S″⊆S′是集覆盖模型(U′,S′)的一个集覆盖,当且仅当P={Cj:SCj∈S″}是覆盖信息系统(U,ζ)的一个覆盖协调集。
证明1) 充分性。设S″⊆S′是集覆盖模型(U′,S′)的一个集覆盖,则∪S″=U′。令P={Cj:SCj∈S″},由定义6可知,要证明P是(U,ζ)的一个覆盖协调集,需要证明Cov(P)≤Cov(ζ),即需要证明对于∀xq∈U,有ΔP(xq)⊆Δζ(xq)。对于∀(xq,xo)∈U′,由定义8可得xo∉Δζ(xq)。又由于U′=∪S″,故(xq,xo)∈S″,从而∃Cj∈P,使得xo∉(xq)Cj,故xo∉ΔP(xq),所以ΔP(xq)⊆Δζ(xq),则Cov(P)≤Cov(ζ)。因此,P是(U,ζ)的一个覆盖协调集。
2) 必要性。设P⊆ζ是覆盖信息系统(U,ζ)的一个覆盖协调集,Cov(P)≤Cov(ζ),则∀xq∈U,有ΔP(xq)⊆Δζ(xq)。令S″=∪{SCi:Ci∈P},对于∀(xq,xo)∈U′,根据定义8可得xo∉Δζ(xq),从而xo∉ΔP(xq),(xq,xo)∈S″,故U′⊆S″。因S″=∪{SCi:Ci∈P}⊆U′,从而S″=U′,即S″是集覆盖模型(U′,S″)的一个集覆盖。
推论2设(U,ζ)是一个覆盖信息系统,ζ={Cj:1≤j≤m},U′={(xp,xo):(xp,xo)∉R,xp∈U,xo∈U},S′={SCj:1≤j≤m},(U′,S′)为(U,ζ)的集覆盖模型。S″⊆S′是集覆盖模型(U′,S′)的一个极小集覆盖,当且仅当P={Cj:SCj∈S″}是覆盖信息系统(U,ζ)的一个覆盖约简集。
证明由定理4容易得证。
3 基于集覆盖模型的覆盖信息系统约简算法
由上述讨论可知,求解覆盖信息系统的属性约简问题可以转化为求解集覆盖模型的极小集覆盖问题。本文选择SCHA来求解覆盖信息系统的属性约简,其在解决SCP上具有更高的精度与更好的性能。下面给出SCHA中用于解决SCP的4个完备策略。
完备策略1:设E={xq:1≤q≤y},S={Sw:1≤w≤r},若∃Sw=E,则选择Sw作为最优化覆盖中唯一一个集合Sw。
完备策略2:设∃x∈E,x只属于Sw,Sw∈S,则选择Sw作为最优化覆盖中的一个集合元素。
完备策略3:若∃S′w和Sw,S′w≠Sw,S′w⊆Sw,则S′w可以被排除。
完备策略4:设∃xp,xq∈E,xp≠xq,用Sn(xp)来表示所有含xp的Sw的集合,若Sn(xp)⊆Sn(xq),则可以将xq从E中删除。
接下来,给出基于SCHA的覆盖信息系统属性约简问题的求解步骤。
输入: 一个覆盖信息系统(U,ζ),其中U={xi:1≤i≤n},ζ={Cj:1≤j≤m}。
输出: 覆盖信息系统(U,ζ)的一个约简RED。
步骤1: 令RED=∅。
步骤2: 根据定义8构造(U,ζ)的相关矩阵M,设矩阵M的行数和列数分别为α、β。
步骤3: 对于矩阵M的第j列(j=1,2,…,β),计算此列中所有行的元素和,若此列中所有行的元素和等于α,则RED=RED∪{Cj},转到步骤8。
步骤4: 对于矩阵M的第i行(i=1,2,…,α),计算此行中所有列的元素和,若此行中所有列的元素和为1,则找出该行中元素值等于1的列,设该列为Sj,则RED=RED∪{Cj},将此列从矩阵中删除,令β=β-1,更新矩阵。


步骤7: 找到矩阵M中所有行元素和最大的列,假定为第j列,令RED=RED∪{Cj},将i从1一直取到α,去除Mij=1所在的行,并且在遍历结束后去除第j列,令α=α-α′,β=β-1,更新矩阵,并返回步骤3。
步骤8: 输出RED。
在基于SCHA求解覆盖信息系统(U,ζ)的属性约简前,首先需要获得(U,ζ)的相关矩阵M,下面给出生成覆盖信息系统(U,ζ)的相关矩阵M的求解算法。
算法1生成覆盖信息系统相关矩阵的算法
输入: 一个覆盖信息系统(U,ζ),其中U={xi:1≤i≤n},ζ={Cj:1≤j≤m}。
输出: 覆盖信息系统(U,ζ)的相关矩阵M。
1:for (p=1;p<=n;p++){
2: for (o=1;o<=n;o++){
3:i=1,a=0;
4: for (j=1;j<=m;j++){
5: if(xo∉(xp)Cj){
6:Mij=1;
7:a=a+1;
8: } else {
9:Mij=0;
10: }
11: }∥end for
12: if(a= =0) 删除第i行;
13: elsei=i+1;
14: }∥end for
15:}∥end for
注:在算法1中,a代表可以区分(xp,xo)的Cj的个数。若a=0,则表示所有Cj均不能区分(xp,xo),故第12行相当于删去R中元素。算法最终得到U′={(xp,xo):(xp,xo)∉R,xp,xo∈U}。
根据上述基于SCHA的覆盖信息系统属性约简问题的求解步骤,下面给出基于SCHA求解覆盖信息系统一个属性约简的相关算法。
算法2基于SCHA的覆盖信息系统属性约简算法
输入: 一个覆盖信息系统(U,ζ),其中U={xi:1≤i≤n},ζ={cj:1≤j≤m}。
输出: 覆盖信息系统(U,ζ)的一个属性约简。
1:求(U,ζ)的相关矩阵M;
2:RED=∅;
3:α=矩阵M的行数;
4:β=矩阵M的列数;
5:HasGetRED=false;
6:while (HasGetRED= =false){
7: for (j=1;j<=RED∪SCj;j++){
8: if(当前Cj列所有行的元素和= =β) {
9:RED=RED∪SCj;
10:HasGetRED=true;
11: returnRED;∥算法结束
12: }∥end if
13: }∥end for
14: for (i=1;i<=α;i++){
15: if(第i行所有列的元素和==1){
16:Mark=元素值为1的元素对应的列号;
17:RED=RED∪SMark;
18:M=M删除Mark列;
19:β=β-1;
20: }∥end if
21: }∥end for
22: for(j=1;j<=β;j++){
23: for (j′=j;j′ <=β;j′++){
24: if(第j列元素为1的元素所在的行构成的集合 ⊂ 第j′列元素为1的元素所在的行构成的集合){
25:M=M删除第j列;
26:S′ =S′-SCj′;
27:β=β-1;
28: }∥end if
29: }∥end for
30: }∥end for
31: for(i=1;i<=α;i++) {
32: for (i′=i;i′<=α;i′++){
33: if (第i行元素为1的元素所在的列构成的集合⊂第i′行元素为1的元素所在的列构成的集合){
34:M=M删除第i′行;
35:α=α-1;
36: }∥end if
37: }∥end for
38: }∥end for
39:Mark=所有行元素和最大的列号;
40:RED=RED∪SMark;
41:α′=Mark列所有行的元素和;
42:Mark2←Mark列元素值为1的元素对应行号的集合;
43:M←M删除Mark2中的行;
44:α=α-α′;
45:β=β-1;
46:S′=S′-SMark;
47:}∥end while
48:将RED中的SCj转化成对应的Cj存入P中。
注:在算法2中,第2行对应基于SCHA的覆盖信息系统属性约简问题的求解步骤1,第3行、第4行对应求解步骤2,第5~13行对应求解步骤3,第14~21行对应求解步骤4,第22~30行对应求解步骤5,第31~38行对应求解步骤6,第39~47行对应求解步骤7,第48行对应求解步骤8。
设m为(U,ζ)的相关矩阵M的行数,n为(U,ζ)的相关矩阵M的列数,则完备策略1的时间复杂度为O(mn),完备策略2的时间复杂度为O(mn),完备策略3的时间复杂度为O(m2n),完备策略4的时间复杂度为O(mn2)。
文献[7]提出的覆盖信息系统约简方法是目前较新的方法之一,与文献[7]不同,本文不需要构造区分矩阵,并且若给定的覆盖信息系统具有符合完备策略1的属性,则本文算法将不再进行后续完备策略2~4的计算,即算法的时间复杂度有可能最小为O(mn)。
4 实例
例1考虑房子评估问题。{价格,结构,颜色,环境}为4个待评估属性集,价格属性值域为{高,中,低},结构属性值域为{合理,一般,差},颜色属性值域为{好,差},环境属性值域为{安静,轻度吵闹,吵闹,非常吵闹}。设有6套房子U1={x1,x2,x3,x4,x5,x6},表1是某公司若干位专家对这6套房子的评估信息表(注:每位专家的评估数据都十分重要,故会出现有的房子某个属性取值为整个值域的情况。例如,房子x3、x4和x6的价格属性值域均为{高,中,低})。为了方便公司对房子进行评估,需要筛选掉冗余属性集(不影响最终分类结果的属性),以减轻评估的工作量。

表1 房子评估信息表Table 1 House appraisal information sheet
用C1代表价格属性,C1中各元素分别代表价格为高、中、低的房子集合,C1={{x1,x2,x3,x4,x6},{x3,x4,x6},{x3,x4,x5,x6}}。
用C2代表结构属性,C2中各元素分别代表结构为合理、一般、差的房子集合,C2={{x1,x2,x3,x4,x5,x6},{x6}}。
用C3代表颜色属性,C3中各元素分别代表颜色为好、差的房子集合,C3={{x1,x2,x3,x6},{x2,x3,x4,x5,x6}}。
用C4代表环境属性,C4中各元素分别代表环境为安静、轻度吵闹、吵闹、非常吵闹的房子集合,C4={{x1,x2,x3,x6},{x2,x3,x4,x5,x6},{x6}}。
C1,C2,C3,C4构成U1的一个覆盖族,令ζ1={C1,C2,C3,C4},则(U1,ζ1)是一个覆盖信息系统。可得Δζ1(x1)={x1,x2,x3,x6},Δζ1(x2)={x2,x3,x6},Δζ1(x3)={x3,x6},Δζ1(x4)={x3,x4,x6},Δζ1(x5)={x3,x4,x5,x6},Δζ1(x6)={x6}。
通过算法1可以得出此覆盖信息系统(U1,ζ1)的相关矩阵M1,如表2所示。
利用算法2对矩阵M1不断进行简化,可以得

表2 覆盖信息系统(U1,ζ1)的相关矩阵M1Table 2 The correlation matrix M1 of covering information system(U1,ζ1)
到覆盖信息系统(U1,ζ1)的覆盖约简集RED1,具体情况如下。
1) 通过遍历矩阵M1,没有发现符合基于SCHA的求解步骤3的列,则从求解步骤4开始分析。通过基于SCHA的求解步骤4发现,矩阵M1第11行所有列的元素和为1,其值为1的列为SC1,将第1列从矩阵M1中删除,并将SC1并入RED1中,得到更新矩阵M2,如表3所示。
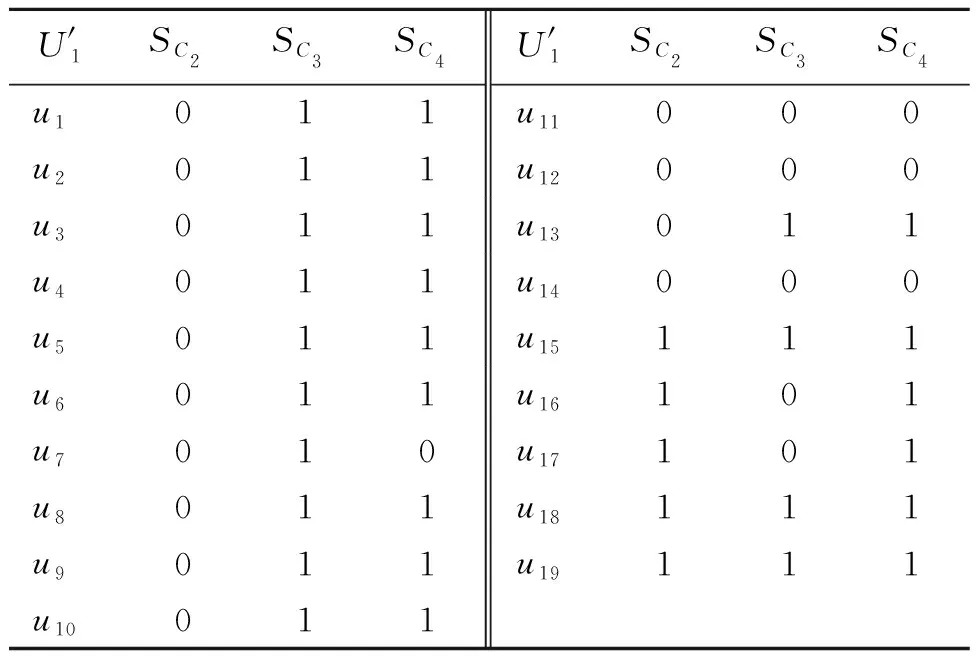
表3 经过求解步骤4后的更新矩阵M2Table 3 The update matrix M2 after solving step 4
2) 继续进行基于SCHA的求解步骤5,通过求解步骤5发现,SC2与SC4符合求解步骤5简化的条件,于是删去SC2这列,得到更新矩阵M3,如表4所示。
3) 通过基于SCHA的求解步骤6,进一步得到更新矩阵M4,如表5所示。

表4 经过求解步骤5后的更新矩阵M3Table 4 The update matrix M3 after solving step 5
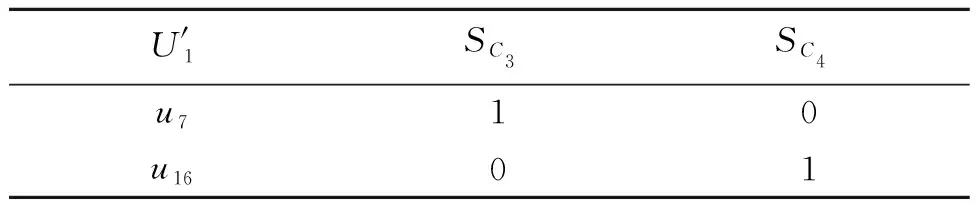
表5 经过求解步骤6后的更新矩阵M4Table 5 The update matrix M4 after solving step 6
4) 最后,通过基于SCHA的求解步骤7得到RED1={C1,C3,C4}。
根据定义4可得ΔRED1(x1)={x1,x2,x3,x6},ΔRED1(x2)={x2,x3,x6},ΔRED1(x3)={x3,x6},ΔRED1(x4)={x3,x4,x6},ΔRED1(x5)={x3,x4,x5,x6},ΔRED1(x6)={x6}。Cov(RED1)≤Cov(ζ1)成立,同时,Cov({C1,C3})≤Cov(ζ1),Cov({C1,C4})≤Cov(ζ1),Cov({C3,C4})≤Cov(ζ1)均不成立,可得RED1={C1,C3,C4}是覆盖信息系统(U1,ζ1)的一个属性约简。{价格,颜色,环境}三个属性是对评估结果具有影响力的属性集,而{结构}属性对评估结果没有影响。因此,当公司在进行实际评估时可以不考虑{结构}属性。
5 结语
本文研究了覆盖信息系统属性约简问题与集覆盖问题的相关性质,构造了覆盖信息系统的相关矩阵,建立了覆盖信息系统属性约简问题与集覆盖问题之间的联系,找到了将覆盖信息系统属性约简问题转化为集覆盖问题的方法,从而可以借助丰富且高效的集覆盖理论来研究覆盖信息系统的属性约简问题。此外,对于有特殊性质的覆盖信息系统属性约简问题,相应的集覆盖解决方法是值得进一步研究的课题。

