基于依赖空间的对象导出三支概念格的属性约简

丁 娜, 马建敏, 贺青青

(长安大学 理学院 陕西 西安 710064)

0 引言

概念格理论[1]作为一种数据分析和信息处理的方法, 已经被广泛应用到信息检索、知识发现、推荐系统、软件工程等领域[2-5]。然而, 随着知识的不断发展, 经典概念格已经不能满足人们的需要, 在描述具体概念时, 不同的刻画方式可以构造出不同的概念格。近来较热门的概念格扩展模型为三支概念格[6], 通过三支算子和三支逆算子定义了两种类型的三支概念格, 即对象导出三支概念格和属性导出三支概念格。三支概念中对象(属性)共同具有的属性(对象)被视为接受的部分, 对象(属性)共同不具有的属性(对象)被视为拒绝的部分, 通过共同具有和共同不具有将研究对象(属性)划分为三个彼此不相交的部分, 这种反映数据隐藏知识的工具更有利于知识发现以及做三支决策[7-9]。学者们从三支概念格的构造、属性约简、规则提取等不同的方面对其研究。Qi等[10]讨论了三支概念格和经典概念格的关系, 同时提出一种基于经典概念格构造三支概念格的方法。Yang等[11]结合原形式背景和其补形式背景的一对概念引入复合算子, 利用复合算子研究三支概念格的构造。Qian[12]通过对三支概念格原形式背景和补形式背景的转换, 结合概念格的构造算法, 提出了三支概念格的构造算法。Ren等[13]提出三支概念格四种类型的属性约简, 并且讨论了它们之间的关系和具体的属性约简方法。张呈玲等[14]在三支概念格的属性约简框架下, 借助布尔矩阵理论, 研究了保持对象导出三支概念对象粒矩阵不变的属性约简问题。

依赖空间理论[15]提供了表达集合独立性和依赖概念的一个通用的框架。Ma等[16]讨论了形式概念分析中基于粗糙集理论的面向对象概念格和面向属性概念格的依赖空间模型, 同时给出了构造这两类概念格的方法。包永伟等[17]主要研究了面向对象概念格和面向属性概念格的依赖空间理论, 为这两类概念格基于一致关系的知识约简与规则提取提供了理论基础。Wang等[18]提出基于一致关系的面向对象概念格属性约简的定义和约简方法。Ma等[19]提出了一种新的构造概念格的方法, 即基于依赖空间构造经典概念格。

本文利用三支算子定义了一致关系, 引入依赖空间, 提出了基于依赖空间的对象导出三支概念格上属性约简的定义, 在此基础上通过引入可辨识属性矩阵和可辨识函数计算约简集。

1 对象导出三支概念格

称三元组(G,M,I)为形式背景, 其中G={x1,x2,…,xn}是非空有限对象集,M={a1,a2,…,am}是非空有限属性集,I⊆G×M是G和M之间的二元关系。对任意x∈G和a∈M, 若(x,a)∈I, 则称对象x具有属性a;若(x,a)∉I, 则称对象x不具有属性a。

在X⊆G和A⊆M上分别定义算子[1]:

X*={a∈M|∀x∈X,(x,a)∈I},

(1)

A*={x∈G|∀a∈A,(x,a)∈I}。

(2)

Qi等[6]在X⊆G和A⊆M上分别定义负算子:

(3)

(4)

根据式(1)～(4)给出的算子, Qi等[6]给出了三支算子和三支逆算子的定义和性质, 进一步提出对象导出三支概念。

定义1[6]设(G,M,I)为形式背景,X⊆G,A,B⊆M。定义三支算子和三支逆算子为

(5)

(6)

性质1[6]设(G,M,I)为形式背景。对任意X,Y⊆G,A,B,C,D⊆M, 下列性质成立:

OEL(G,M,I)表示形式背景(G,M,I)上所有对象导出三支概念的集合。对任意(X,(A,B)),(Y,(C,D))∈OEL(G,M,I), 定义OEL(G,M,I)上的偏序关系≤:

(X,(A,B))≤(Y,(C,D))⟺X⊆Y⟺(C,D)⊆(A,B),

则(OEL(G,M,I),≤)是一个完备格, 称为对象导出三支概念格[6], 其下确界和上确界分别为

(X,(A,B))∧(Y,(C,D))=

(X,(A,B))∨(Y,(C,D))=

记ExtOEL(G,M,I)={X|(X,(A,B))∈OEL(G,M,I)}为对象导出三支概念所有外延构成的集合,IntOEL(G,M,I)={(A,B)|(X,(A,B))∈OEL(G,M,I)}为对象导出三支概念所有内涵构成的集合。

2 基于依赖空间的对象导出三支概念格

本节在对象幂集上定义一致关系, 引入依赖空间, 在此基础上讨论闭包算子的闭元素与对象导出三支概念的外延之间的关系。

定义3[15]设V为非空有限集合,K为幂集P(V)上的等价关系。

1) 若对任意(B1,C1)∈K,(B2,C2)∈K, 有(B1∪B2,C1∪C2)∈K, 则称K为P(V)上的一致关系;

2) 若K为P(V)上的一致关系, 则称(V,K)为依赖空间。

定理1设(G,M,I)为形式背景,N⊆M。定义P(G)上的二元关系为

(7)

定义4[1]设(P,≤)是偏序集。若映射c:P→P满足条件

1) 对任意x∈P,x≤c(x),

2) 对任意x,y∈P,x≤y⟹,c(x)≤c(y),

3) 对任意x∈P,c(c(x))=c(x),

则称c是(P,≤)上的闭包算子。

定理2设(G,M,I)为形式背景。对任意X,Y⊆G,N⊆M, 定义

则

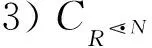
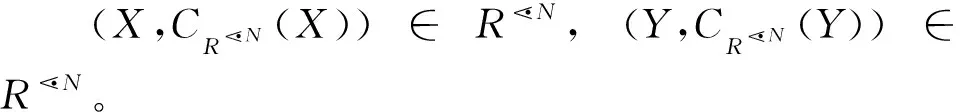
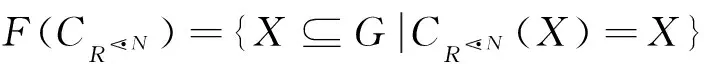
引理1设(G,M,I)为形式背景。对任意X⊆G和N⊆M, 有

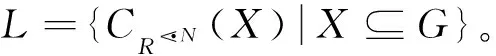
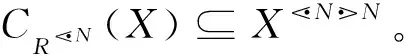
由性质1中的3)和引理1中的2)得, 对任意X⊆G,N⊆M,

(8)

定理3设(G,M,I)为形式背景。对任意X⊆G和A,B⊆M, 有

(9)

3 基于依赖空间的对象导出三支概念格的属性约简

本节提出基于依赖空间的对象导出三支概念格上属性约简的定义, 给出协调集的判定定理, 借助可辨识属性矩阵及辨识函数给出属性约简方法。

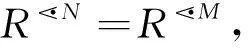
定理4设(G,M1,I1),(G,M2,I2)为具有相同对象集的两个形式背景。则

由定义5和定理4可得推论1。

推论1设(G,M,I)为形式背景。对任意N⊆M,N是(G,M,I)的属性约简,

1)ExtOEL(G,N,IN)=ExtOEL(G,M,I);

2) 对任意a∈N,

ExtOEL(G,N-{a},IN-{a})≠ExtOEL(G,M,I)。

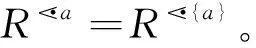
定义6设(G,M,I)为形式背景。对任意X,Y⊆G, 定义

为可辨识属性矩阵。

定理5设(G,M,I)为形式背景。对任意X,Y⊆G, 有

(A∪C-A∩C)∪(B∪D-B∩D),

因此,

性质2设(G,M,I)为形式背景。对任意X,Y,Z⊆G,N⊆M, 性质1)～4)成立:

2)

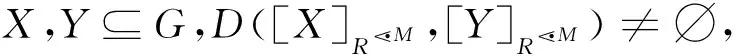
证明1) ⟹。设N是协调集, 则

则由定理5有(A∩N,B∩N)≠(C∩N,D∩N)。

下证对任意(X,(A,B))∈OEL(G,M,I)有(X,(A∩N,B∩N))∈OEL(G,N,IN)。

得

但是, 一方面由(A∩N,B∩N)⊆(A,B)得

另一方面, 由

得

矛盾。故

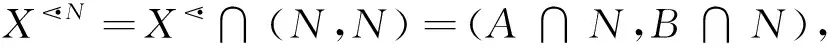
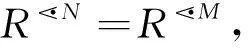
通过使用吸收律和分配律, 可以将辨识函数f(Λ)变换为最小析取范式, 这个最小析取范式的所有组成成分是形式背景的全部约简。

例1考虑形式背景(G,M,I), 如表1,其中G={1,2,3,4},M={a,b,c,d,e}。

表1 形式背景(G,M,I)Table 1 The formal context(G,M,I)

2) 计算所有等价类:

OEL(G,M,I)={(∅,(M,M)), (1,(abde,c)), (2,(abc,de)),(3,(d,abce)), (4,(abce,d)), (13,(d,c)),(23,(∅,e)), (14,(abe,∅)), (24,(abc,d)),(124,(ab,∅)), (G,(∅,∅))}。

对象导出三支概念格如图1所示。

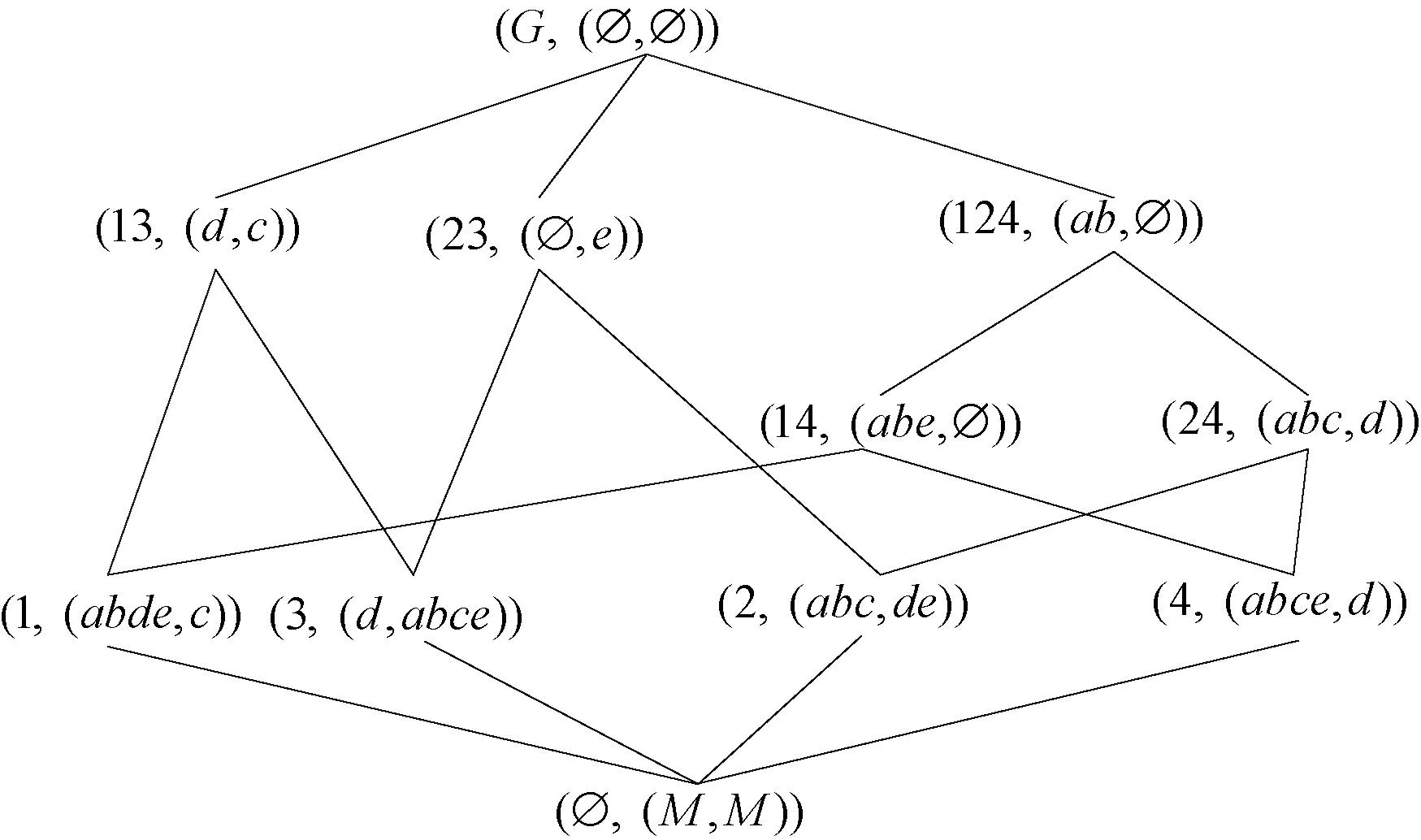
图1 (G,M,I)的对象导出三支概念格Figure 1 The object-induced three-way concept lattice of (G,M,I)

4) 由对象导出三支概念计算可辨识属性矩阵Λ, 如表2。

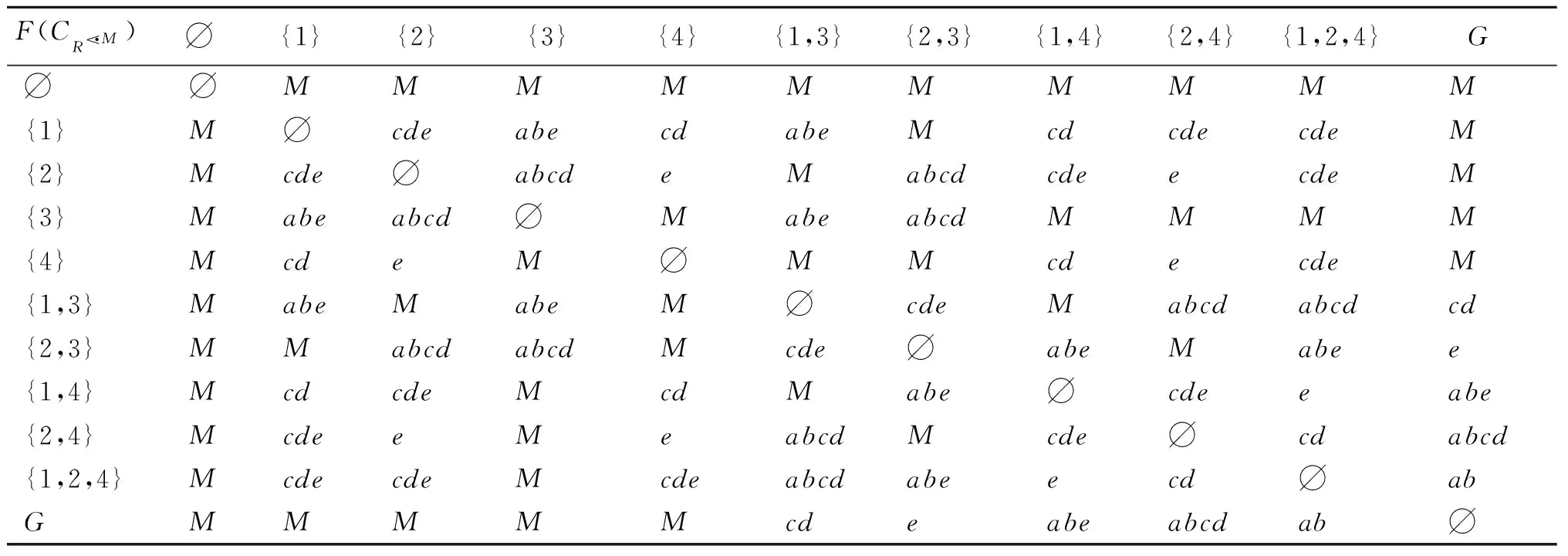
表2 (G,M,I)的可辨识属性矩阵Table 2 The discernibility matrix of (G,M,I)

5) 计算形式背景(G,M,I)的辨识函数:

f(Λ)=(a∨b∨c∨d∨e)∧(c∨d∨e)∧

(a∨b∨e)∧(c∨d)∧(a∨b∨c∨d)∧e∧(a∨b)=(a∧c∧e)∨(a∧d∧e)∨(b∧c∧e)∨(b∧d∧e)。

因此对象导出三支概念格的约简集分别为{a,c,e},{a,d,e},{b,c,e},{b,d,e}。

4 结论

本文基于依赖空间证明了闭包算子的闭元素是对象导出三支概念的外延。在此基础上提出了基于一致关系的对象导出三支概念格属性约简的定义, 该定义下的约简集是保持由原属性集确定的一致关系不变的最小属性子集。最后利用可辨识属性矩阵的方法计算对象导出三支概念格的属性约简集。

下一步将研究基于依赖空间的属性导出三支概念格的属性约简方法, 进一步研究基于一致关系的对象导出三支概念格的规则提取方法。