一般决策形式背景的属性约简
谢业海, 高秀巍
(北京语言大学 信息科学学院 北京 100083)
0 引言
1982年,德国学者Wille[1]提出了形式概念分析理论,也被称作概念格理论。形式概念分析理论通过构建一个概念完备格,直观地刻画出概念之间的层次结构,因而成为一种有效的数据处理工具,被广泛应用于信息检索、数据挖掘等领域[2-3]。
面对海量数据,如何去除冗余信息,保留核心信息,降低数据的维度和计算复杂度,对于数据处理来说十分重要,因此属性约简[4-5]一直受到广泛的关注。概念格的属性约简本质上是在保持概念格某个特性不变的基础上,寻找最小属性集,使约简后的概念格比原概念格更加简洁,因而概念格的属性约简一直都是热点研究问题。Zhang等[6]首先提出保持概念格结构不变的约简,即约简后的概念格与原概念格同构,并基于辨识矩阵给出获得所有约简的算法。Qi[7]对文献[6]中的辨识矩阵加以改进,获得了计算效率更高的约简算法。Wu等[8]从粒计算的角度定义了概念格的对象粒,并用对象粒去定义形式背景的粒约简,同时给出获得相应约简的方法。许多学者研究粗糙集的属性约简和形式背景的属性约简之间的关系。Wei等[9]将形式背景当作一个属性值为0和1的信息系统,并研究了形式背景属性约简和信息系统绝对约简之间的关系。Liu等[10]研究了面向对象的概念格的属性约简与信息系统的属性约简之间的关系。Li等[11]定义了形式背景的不可约简属性类,并用不可约简属性类刻画了形式背景的核心属性集、相对必要属性集和冗余属性集,同时给出了约简的判定定理。Ren等[12]研究了三支概念格的属性约简问题,在对象导出三支概念格和属性导出三支概念格中分别定义了4种约简,并研究了约简之间的关系,同时给出了其中7种约简的计算方法。魏玲等[13]研究了强协调决策形式背景和弱协调决策形式背景的约简定义和约简方法。决策形式背景的提出,进一步丰富了形式概念分析的理论,得到了学术界的广泛关注。Li等[14]面向规则提取,定义了决策形式背景的约简,并给出计算所有约简的算法。在文献[8]中,Wu等定义了一致决策形式背景的粒约简并给出相应约简算法。Wang等[15]基于辨识矩阵,给出了计算广义一致决策形式背景约简的算法。
相对一致决策形式背景而言,不一致决策形式背景在实际应用中更为常见,因此研究一般决策形式背景的属性约简更具有现实意义。基于此,本文给出一般决策形式背景的属性约简的定义,并利用辨识函数给出计算所有约简的算法。该算法可应用于一致决策形式背景和不一致决策形式背景。特别地,文献[13]中的强协调决策形式背景的约简是我们算法的特例。
1 形式概念分析的基本定义及性质
本节介绍形式概念分析的基础知识,包括形式背景、决策形式背景、概念、概念格的定义及相关性质。
定义1[1]形式背景是一个三元组(U,A,I),U是非空有限对象集,A是非空有限属性集,I是U和A之间的二元关系,即I⊆U×A。
对于一个形式背景(U,A,I),可在对象集和属性集上定义两个运算[16],
∀X⊆U,X*={a∈A|∀x∈X,xIa},
∀B⊆A,B*={x∈U|∀b∈B,xIb},
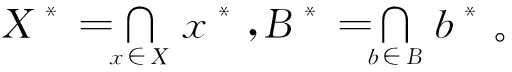
设(U,A,I)为一个形式背景,对于B⊆A,令IB=I∩(U×B),则(U,B,IB)也是一个形式背景[6]。为了区分不同形式背景下的“*”运算,我们分别用“*A”和“*B”表示形式背景(U,A,I)和(U,B,IB)中的“*”运算。对于C⊆B⊆A,容易证明有C*A=C*B[8]。
设(U,A,I)为一个形式背景,其中对象集为U={x1,x2,…,xm},属性集为A={a1,a2,…,an}。将(U,A,I)视为一张m行n列的信息表,其中信息表中元素的值域为{0,1}。若信息表中第i行第j列的元素为1,则表示(xi,aj)∈I,即对象xi具有属性aj,反之则表示(xi,aj)∉I,即对象xi不具有属性aj。若形式背景(U,A,I)对应的信息表的每行每列既有0又有1,则称(U,A,I)是正则的[6]。本文研究的形式背景在约简前均为正则的。
定义2[16]假设(U,A,I)为形式背景,∀X⊆U,∀B⊆A,若X*A=B且B*A=X,则称二元组(X,B)为形式背景(U,A,I)的概念,称X为概念(X,B)的外延,B为概念(X,B)的内涵。
记形式背景(U,A,I)的全体概念为L(U,A,I),即L(U,A,I)={(X,B)|X⊆U,B⊆A,X*A=B,B*A=X};记全体概念的外延集为LU(U,A,I),即LU(U,A,I)={X⊆U|B⊆A,(X,B)∈L(U,A,I)}。对于任意(X1,B1),(X2,B2)∈L(U,A,I),定义L(U,A,I)上的偏序关系为
(X1,B1)≤(X2,B2)⟺X1⊆X2⟺B2⊆B1。
若(X1,B1),(X2,B2)∈L(U,A,I),在L(U,A,I)上分别定义上、下确界为
(X1,B1)∧(X2,B2)=(X1∩X2,(B1∪B2)*A*A),
(X1,B1)∨(X2,B2)=((X1∪X2)*A*A,B1∩B2),
则L(U,A,I)为完备格,称之为形式背景(U,A,I)的概念格。
性质1假设(U,A,I)为形式背景,对于∀X,X1,X2⊆U和∀B,B1,B2⊆A,容易证明有性质1)~5)[16]:
1)X1⊆X2⟹X1*A⊇X2*A,B1⊆B2⟹B1*A⊇B2*A;
2)X⊆B*A⟺B⊆X*A;
3)X⊆X*A*A,B⊆B*A*A;
4)X*A=X*A*A*A,B*A=B*A*A*A;
5)(X*A*A,X*A)∈L(U,A,I),
(B*A,B*A*A)∈L(U,A,I)。
定义3[6]设(U,A1,I1)和(U,A2,I2)为形式背景,若LU(U,A2,I2)⊆LU(U,A1,I1),则称L(U,A1,I1)细于L(U,A2,I2),记为L(U,A1,I1)≤L(U,A2,I2)。
若L(U,A1,I1)≤L(U,A2,I2),那么对于任意(X2,B2)∈L(U,A2,I2),总存在(X1,B1)∈L(U,A1,I1)使得X1=X2。
设(U,A,I)为形式背景,∅≠B⊆A,那么不难验证有L(U,A,I)≤L(U,B,IB)[6]。
定义4令(U,A,I)和(U,T,J)为形式背景,则称五元组(U,A,I,T,J)为决策形式背景[13]。其中,A是条件属性集,T是决策属性集。若L(U,A,I)≤L(U,T,J),则称(U,A,I,T,J)为一致的决策形式背景,反之则称(U,A,I,T,J)为不一致的决策形式背景。
定义4中的一致决策形式背景即是文献[13]中定义的强协调决策形式背景。
2 一般决策形式背景的广义约简
对一般决策形式背景,定义一种新的约简,该约简是强协调决策形式背景的约简的扩展。需要指出的是,作为一个特例,用本节提出的约简算法,可获得强协调决策形式背景的所有约简。
设(U,A,I,T,J)为决策形式背景,对于∅≠B⊆A,记VB=LU(U,B,IB)∩LU(U,T,J),于是VA=LU(U,A,I)∩LU(U,T,J)。
定义5令(U,A,I,T,J)为决策形式背景,∅≠B⊆A,若B满足
1)VA=VB,
2) 对于任意∅≠C⊂B,那么VC≠VA,
则称B为决策形式背景(U,A,I,T,J)的约简。
特别地,若(U,A,I,T,J)为一致决策形式背景,那么VA=LU(U,T,J),则VA=VB等价于L(U,B,IB)≤L(U,T,J)。
引理1假设(U,A,I)为形式背景,则有
1)∀a∈A,(a*A,a*A*A)∈L(U,A,I);
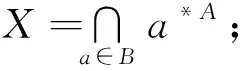
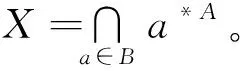
证明1) 对于∀a∈A,根据性质1中的4)有a*A=a*A*A*A,那么有(a*A,a*A*A)∈L(U,A,I)。

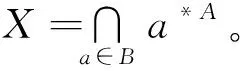

定理1设(U,A,I,T,J)为决策形式背景,对于任意∅≠B⊆A,条件1)和2)等价:
1)VA=VB;
2)对于∀X∈VA且X≠U,存在C⊆B,使得X=C*A。
证明1)⟹2):若VA=VB,对于∀X∈VA且X≠U,有X∈VB,也就是∃C⊆B使(X,C)∈L(U,B,IB)。由定义2可知有X=C*B,又C*A=C*B,所以X=C*A。
2)⟹1):由∅≠B⊆A,有L(U,A,I)≤L(U,B,IB),也就是LU(U,B,IB)⊆LU(U,A,I),所以VB⊆VA。
下面证VA⊆VB。当X∈VA且X=U时,显然有X∈VB。当∀X∈VA且X≠U时,由2)可知存在C⊆B使得X=C*A,又由C*A=C*B可推出X=C*B,由引理1中3)可推出X∈LU(U,B,IB),即X∈VB,所以有VA⊆VB。综上可得VA=VB。
推论1设(U,A,I,T,J)为决策形式背景,∅≠B⊆A,则B是(U,A,I,T,J)的约简,当且仅当B是A的满足定理1中2)的极小子集。
在决策形式背景(U,A,I,T,J)中,对于X∈VA且X≠U,记(X)={C⊆A|X∈VA,X≠U,X=C*A},min(X)={D∈(X)|∀C∈(X),C≠D,C⊄D}。由推论1可得计算一般决策形式背景约简的算法。
算法1一般决策形式背景的约简算法
输入: 一般决策形式背景(U,A,I,T,J)。
输出: 全部约简。
步骤1 计算VA=LU(U,A,I)∩LU(U,T,J)。
步骤2 对于∀X∈VA且X≠U,计算min(X)。

算法1中的辨识函数是一个由辨识矩阵诱导的单调布尔函数。辨识矩阵和辨识函数最初由Skowron等[17]应用于粗糙集的属性约简中。设M=(Cij)m×n为一个辨识矩阵,其中矩阵中的元素Cij为属性的集合,那么M可诱导一个辨识函数f=∧{∨(Cij):1≤i≤m,1≤j≤n,Cij≠∅}。将辨识函数f由合取范式转换为最小析取范式后,其中任意一个质蕴涵项中的所有属性组成的集合即为一个约简,所有质蕴含项对应的约简组成的集合即为所有约简的集合。在算法1中,根据定理1可知,对于X∈VA且X≠U,(X)={C⊆A|X∈VA,X≠U,X=C*A}是辨识函数f对应的辨识矩阵中的非空元素。由于在将辨识函数f转换为最小析取范式的过程中会使用吸收率,所以取min(X)以简化计算过程。
算法1中的步骤2是构造辨识函数的基础,也是本文的主要研究成果,所以仅讨论步骤2的时间复杂度。设(U,A,I,T,J)为一般决策形式背景,X∈VA且X≠U,(X,B)∈L(U,A,I),记B的幂集为P(B),步骤2计算min(X)时,首先要计算(X)={C⊆A|X∈VA,X≠U,X=C*A}。为了计算出(X),对于∀C∈P(B),要计算C*A并判断C*A是否等于X,若C*A=X,则将C作为元素加入集合(X)中,这也是步骤2中时间复杂度最高的环节,所以步骤2的时间复杂度为O(|U||A|2|A|)。用文献[13]中的约简方法对一致决策形式背景进行约简时,计算辨识矩阵的时间复杂度为O((|U|+|A|)|A||L(U,T,J)|)[18],低于算法1中步骤2的时间复杂度。但是算法1可应用于不一致决策形式背景的属性约简,因此比文献[13]中的方法应用范围更广。
下面用一个例子对算法1进行说明。
例1设决策形式背景Γ=(U,A,I,T,J)如表1所示,其中:对象集U={1,2,3,4,5};条件属性集A={a,b,c,d,e};决策属性集T={f,g,h}。
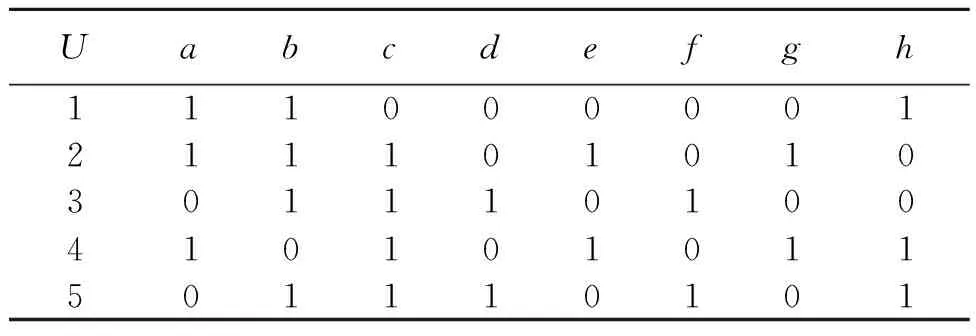
表1 一个不一致决策形式背景Table 1 An inconsistent decision formal context
在决策形式背景Γ中,L(U,A,I)和L(U,T,J)的哈斯图分别如图1、图2所示。可以看到,形式背景(U,A,I)共有10个概念,形式背景(U,T,J)共有7个概念。由于(145,h)∈L(U,T,J)但{1,4,5}∉LU(U,A,I),所以Γ是不一致决策形式背景。

图1 例1中概念格L(U,A,I)的哈斯图Figure 1 The Hasse diagram of L(U,A,I) in example 1
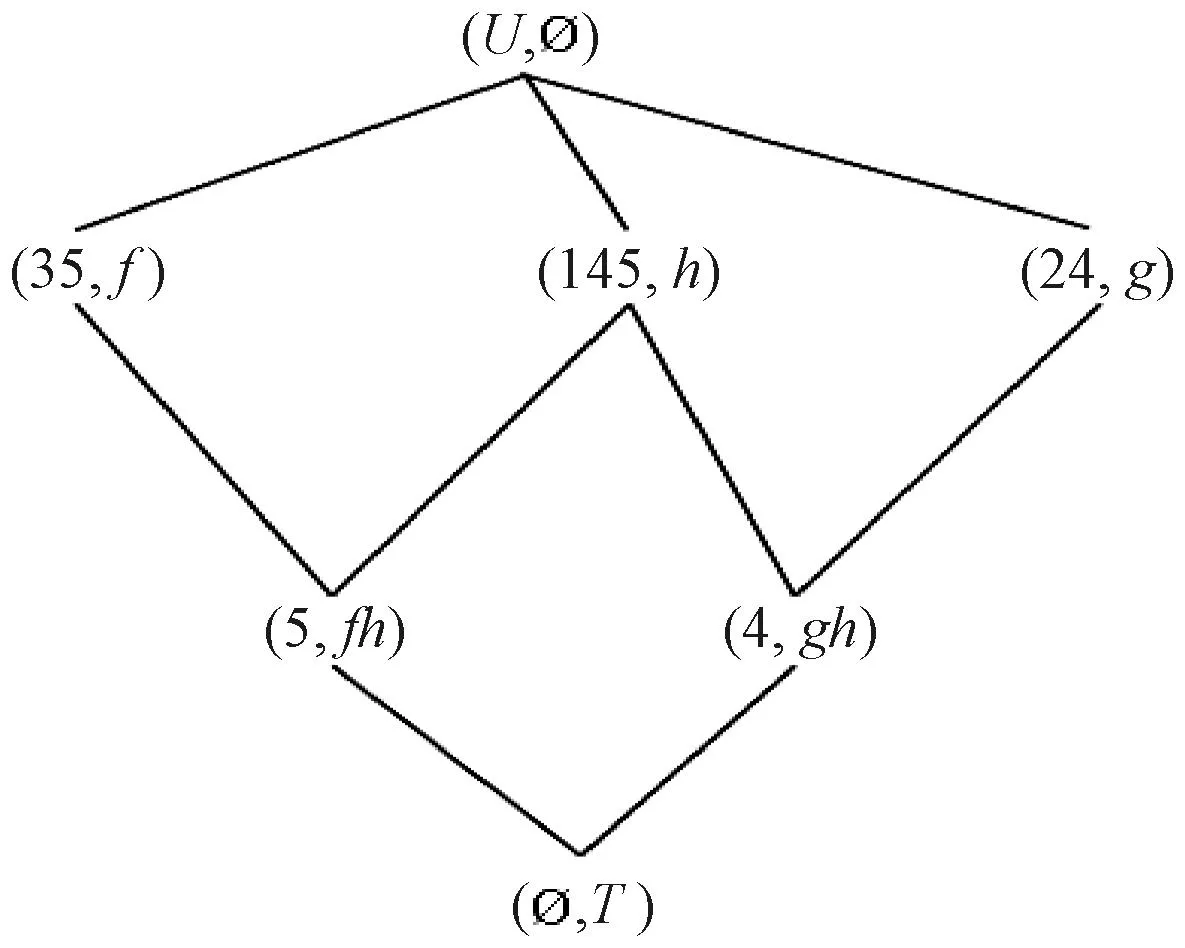
图2 例1中概念格L(U,T,J)的哈斯图Figure 2 The Hasse diagram of L(U,T,J) in example 1
约简的具体计算过程如下。
第一步 计算得到VA={∅,{2,4},{3,5},U}。
第二步 对于∀X∈VA且X≠U,计算min(X)得
min(∅)={{a,d},{d,e}},
第三步 构造辨识函数
f=((a∧d)∨(d∧e))∧(e∨(a∧c))∧d。
第四步 将辨识函数转换为最小析取范式
f=(a∧c∧d)∨(d∧e)。
第五步 得到所有约简为{a,c,d}和{d,e}。
令B={a,c,d},约简后的概念格L(U,B,IB)的哈斯图如图3所示。由图1~3可以看到,LU(U,A,I)={∅,{2},{1,2},{2,4},{3,5},{1,2,4},{2,3,5},{1,2,3,5},{2,3,4,5},U},LU(U,T,J)={∅,{4},{5},{2,4},{3,5},{1,4,5},U},LU(U,B,IB)={∅,{2,4},{3,5},{1,2,4},{2,3,4,5},U},那么VB=LU(U,B,IB)∩LU(U,T,J)={∅,{2,4},{3,5},U}=VA,约简后有VB=VA。B={a,c,d}是一个约简。
假设(U,A,I,T,J)为强协调决策形式背景,那么VA=LU(U,T,J)。
定理2设(U,A,I,T,J)为强协调决策形式背景,对于任意∅≠B⊆A,条件1)和2)等价:
1)VA=VB;
2)L(U,B,IB)≤L(U,T,J)。
证明由于(U,A,I,T,J)为强协调决策形式背景,那么有VA=LU(U,T,J)。
1)⟹2):由VA=VB=LU(U,B,IB)∩LU(U,T,J)及VA=LU(U,T,J),有LU(U,T,J)=LU(U,B,IB)∩LU(U,T,J),可以推出LU(U,T,J)⊆LU(U,B,IB),即L(U,B,IB)≤L(U,T,J)。
2)⟹1):由L(U,B,IB)≤L(U,T,J)可得LU(U,T,J)⊆LU(U,B,IB),那么VB=LU(U,B,IB)∩LU(U,T,J)=LU(U,T,J),又由VA=LU(U,T,J),所以VA=VB。
若(U,A,I,T,J)为强协调决策形式背景,则使用算法1和使用文献[13]中的算法对(U,A,I,T,J)进行约简,得到的结果一致。下面引用文献[13]中的例子对定理2进行说明。
例2设决策形式背景Γ=(U,A,I,T,J)如表2所示,其中对象集U={1,2,3,4,5},条件属性集A={a,b,c,d,e},决策属性集T={f,g,h}。
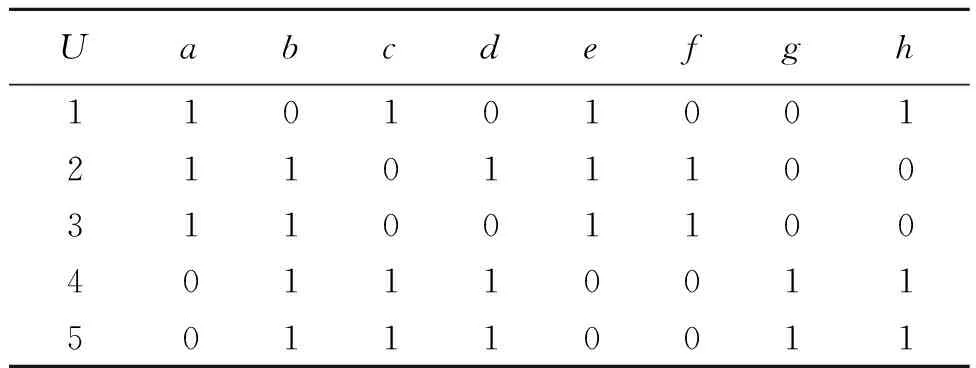
表2 一个一致决策形式背景Table 2 A consistent decision formal context
在决策形式背景Γ中,L(U,A,I)和L(U,T,J)的哈斯图分别如图4、图5所示,可以看到(U,A,I)共有10个概念,(U,T,J)共有5个概念。不难看出,Γ为一致决策形式背景。
约简的具体计算过程如下。
第一步 计算得到VA={∅,{2,3},{4,5},{1,4,5},U}。
第二步 对于∀X∈VA且X≠U,计算min(X)得
min(∅)={{a,b,c},{b,c,e},{c,d,e},{a,c,d}},
min(23)={{a,b},{b,e}},
第三步 计算辨识函数得到
f=((a∧b∧c)∨(b∧c∧e)∨
(c∧d∧e)∨(a∧c∧d))∧((a∧b)∨
(b∧e))∧((b∧c)∨(c∧d))∧c。
第四步 将辨识函数转换为最小析取范式
f=(a∧b∧c)∨(b∧c∧e)。
第五步 得到所有约简为{a,b,c}和{b,c,e}。
可以看到,算法1的约简结果与文献[13]中的一致。令B={a,b,c},约简后的概念格L(U,B,IB)的哈斯图如图6所示,不难验证VB=VA。
3 结论
本文研究一般决策形式背景的属性约简方法,提出一般决策形式背景的属性约简的定义,并给出可计算所有约简的算法。未来,我们将从信息损失、计算效率等方面对比约简前、后决策形式背景在不同应用场景中的区别。
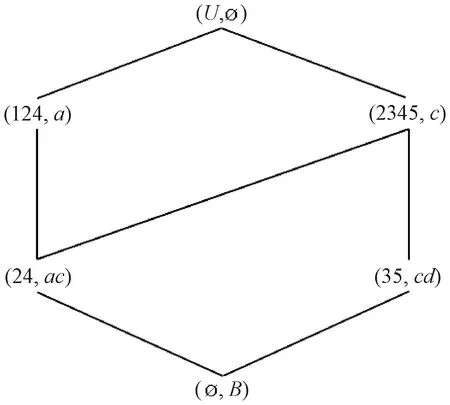
图3 例1中概念格L(U,B,IB)的 哈斯图Figure 3 The Hasse diagram of L(U,B,IB) in example 1

图4 例2中概念格L(U,A,I)的哈斯图Figure 4 The Hasse diagram of L(U,A,I) in example 2
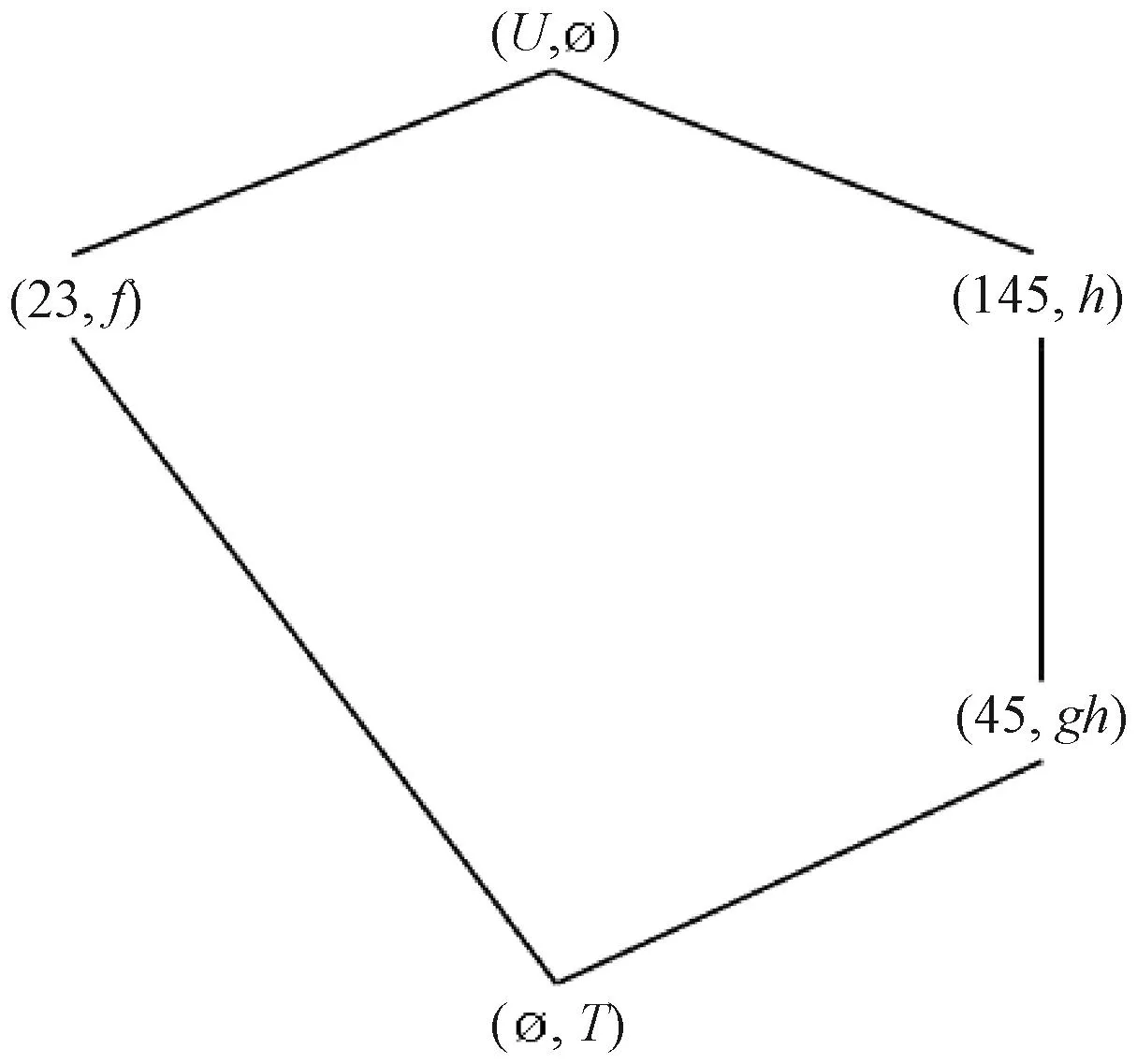
图5 例2中概念格L(U,T,J)的 哈斯图Figure 5 The Hasse diagram of L(U,T,J) in example 2

图6 例2中概念格L(U,B,IB)的哈斯图Figure 6 The Hasse diagram of L(U,B,IB) in example 2

