Self-Consistent Sources Extensions of Modified Differential-Difference KP Equation∗

Gegenhasi(葛根哈斯), Ya-Qian Li(李雅倩),and Duo-Duo Zhang(张朵朵)

School of Mathematical Sciences,Inner Mongolia University,Hohhot 010021,China

1 Introduction

Seeking new integrable system is an important aspect of the theory of integrable system. The soliton equation with self-consistent sources is an integrable generalization of the original integrable equation.Soliton equations with self-consistent sources also have important applications in hydrodynamics,plasma physics,and solid state physics.For example,the KdV equation with selfconsistent sources describes the interaction between long and short capillary gravity waves in hydrodynamics and coupling of a plasma wavepacket to acoustic waves in plasma physics.[1]The KP equation with self-consistent sources describes the interaction of a long wave with a short-wave packet propagating on the x,y plane at an angle to each other.[2−3]Various methods such as the inverse scattering methods,[4−8]Darboux transformation methods.[9−14]Hirota’s bilinear method and Wronskian technique,[15−21]deformations of binary Darboux transformations[22−23]have been developed to study the soliton equations with self-consistent sources.In Ref.[24],the authors proposed a new algebraic method,called the source generation procedure to generate and solve the soliton equations with self consistent sources both in continuous and discrete cases in a unified way.

The differential-difference KP equation is an integrable semi-discretization of the KP equation.It takes the following form[25−26]

where Vndenotes V(n,y,t)and△denotes the forward difference operator defined by△fn=fn+1−fn.

Through the dependent variable transformation

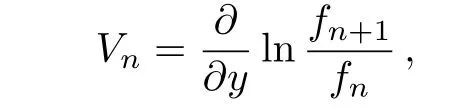
Eq.(1)istransformed into the following bilinear eqaution[25−26]

where the bilinear operatorsand eDnare defined by[27]

A bilinear Bäcklund transformation for the bilinear differential-difference KP equation(2)is written as[28]

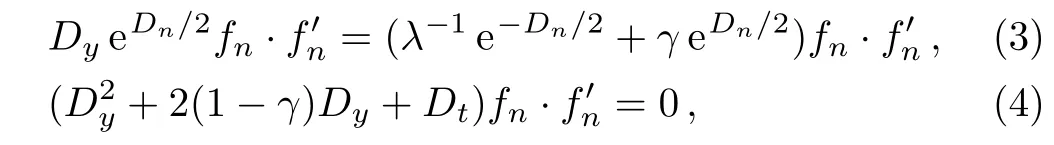
where λ is a nonzero constant and γ is an arbitrary constant.By introducing new dependent variables Un=(ln)y,wn=ln,Eqs.(3)–(4)are transformed into the following nonlinear equations

It is not difficult to show that the solution Vnof differential-difference KP Eq.(1)is related to the solution wn,Unof the modified differential-difference KP equations(5)–(6)by the Miura transformation Vn=wn,y− Un.In fact,from Eq.(5),we derive

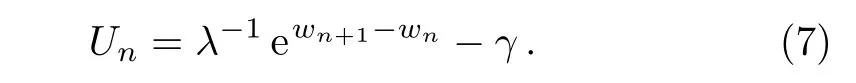
Substituting Vn= γ − λ−1ewn+1−wn+wn,yinto the left side of Eq.(1),and applying Eqs.(6)–(7),the left side of Eqs.(1)becomes

which also can be derived by substituting Vn=γ−λ−1ewn+1−wn+wn,yinto the right side of Eq.(1).

If we take Wn=wn,y=(lnf′n/fn)y,the nonlinear differential-difference Eqs.(5)–(6)become

We call Eqs.(3)–(4)or(8)–(9)the modified differential difference KP equation.It is easy to know that Vn=Wn−Unis a Miura transformation connecting the solutions of the differential-difference KP equation(1)and the modified differential-difference KP equations(8)–(9).

The paper is organized as follows.In Sec.2,we first derive the N-soliton solution of the modified differential difference KP equations(5)–(6)in the form of the Grammian determinants,and then construct the modified differential-difference KP equation with self-consistent sources applying the source generation procedure. In Sec.3,the N-soliton solution in Casoratian form for the modified differential-difference KP equation with selfconsistent sources is given.In Sec.4,we produce and solve another form of the modified differential-difference KP equation with self-consistent sources which is a Bäcklund transformation for the differential-difference KP equation with self-consistent sources.Section 5 is devoted to a conclution and discussion.

2 The Modified Differential-Difference KP Equation Equation with Self-consistent Sources

In Ref.[28],the Casorati determinant solution for the modified differential-difference KP equations(3)–(4)was given.In this section,we first compactly express N-soliton solution to the modified differential-difference KP equations(3)–(4)in a Grammian form,then generate the modified differential-difference KP equation with self-consistent sources by using the source generation procedure.

If we take λ = −1,γ =1,Eqs.(3)–(4)and(8)–(9)become

and

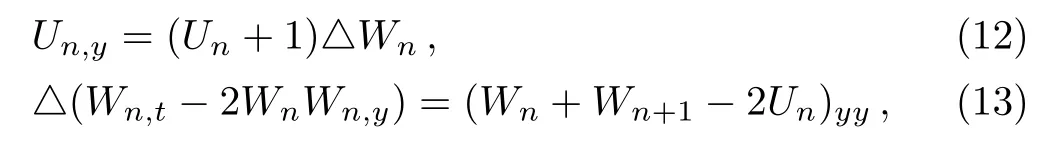
respectively.

A continuum limit of the modified differential-difference KP equation(10)–(11)or(12)–(13)gives the mKP equation.This can be seen most easily from the bilinear form by setting

in(10)–(11)and comparing ϵ3order in Eq.(10), ϵ2order in Eq.(11)to obtain the mKP equation in bilinear form:[29−30]

Proposition 1The modified differential-difference KP equations(10)–(11)have the following Grammian determinant solution:

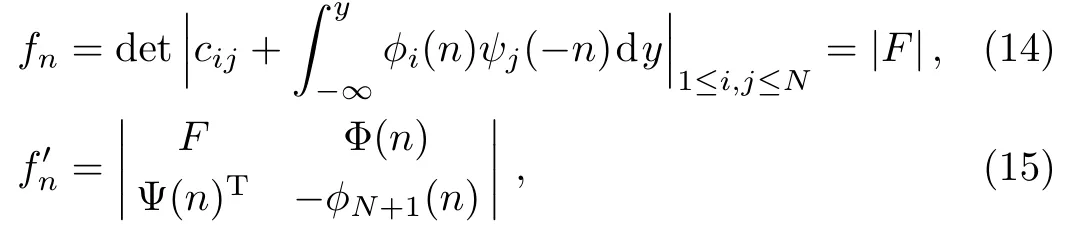
where Φ(n),Ψ(n)are N-th column vectors defined by

In addition,cij(1≤i,j≤N+1)are arbitrary constants,ϕi(n),ψi(−n)(i=1,...,N+1)are functions of n,y,t,and satisfy the following dispersion relations:

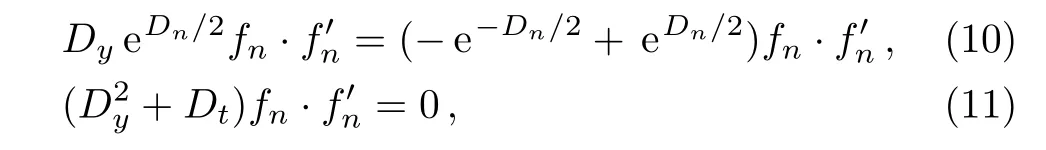
The proof of the Proposition 1 will be given in the later part of the Sec.2.

Now we construct the modified differential-difference KP equation with self-consistent sources applying the source generation procedure.We change the Grammian determinant solutions(14)–(15)into the following form:

where N-th column vectors Φ(n),Ψ(n)are given in Eqs.(16)–(17)and ϕi(n),ψi(−n)(i=1,...,N+1)also satisfy the dispersion relations(18)–(20). In addition,γij(t)satis fies

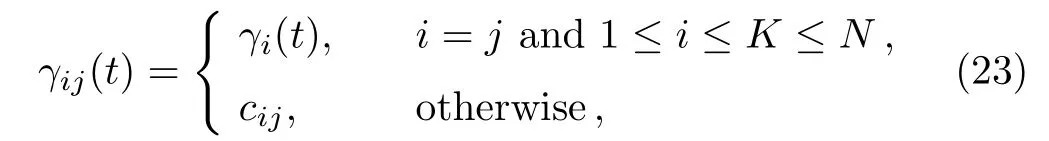
with γi(t)being an arbitrary nondecreasing function of t and K being a positive integer.

The Grammian determinants τnin Eq.(21)andin Eq.(22)can be expressed by means of the following pfaffians:

where the pfaffian elements are defined by

in which i,j=1,...,N+1 and k,m are integers.

It is easy to show that the functions τn,given in Eq.(24)still satisfy Eq.(10):

However,they will not satisfy Eq.(11),and they satisfy the following new equation:

where new functions gj,n,hj,n(j=1,...,K)are given by

where the dot denotes the derivative of γj(t)with respect to t.Furthermore,we can show that τn,(j=1,...,K)satisfy the following 2K equations:

Therefore,Eqs.(27)–(28),(31)–(32)constitute the modified differential-difference KP equation with selfconsistent sources.In the following,we show that the Grammmian determinants(24),(29)–(30)are solutions to the modified differential-difference KP equation with self-consistent sources(27)–(28),(31)–(32).

Using the dispersion relations(18)–(20),we can derive the following differential and difference formula for(j=1,...,K):

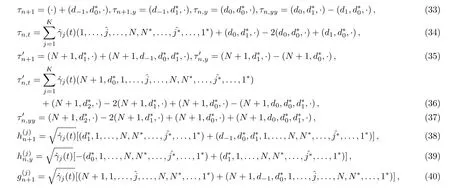
whereˆindicates deletion of the letter under it.

By substituting Eqs.(33)–(41)into Eqs.(28),(31)–(32)we obtain the following determinant identities:

and

respectively.

When γij(t)= ci,j(1 ≤ i,j ≤ N),where ci,j(1≤i,j≤N)are arbitrary constants,the Grammian determinants τn,are reduced to the Grammian determinants fn,respectively,and==0,j=1,...,K.Consequently,the modified differential-difference KP equation with self-consistent sources(10),(28),(31)–(32)are reduced to the modified differential-difference KP equation(10)–(11).Therefore,the Proposition 1 holds.

Through the dependent variable transformations

the modified differential-difference KP equation with selfconsistent sources(27)–(28),(31)–(32)can be transformed into the following nonlinear equations

In order to obtain the N-soliton solution of the modified differential-difference KP equation with self-consistent sources(45)–(48),we take

for i=1,2,...,N+1 in the Grammian determinants(14)–(15),(29)–(30).Here pi,qi,(i=1,2,...,N+1)are real arbitrary constants,

For example,if we take K=1,N=1 and

where a(t)isa function oftsatisfying γ1(t) =e2a(t)/(p1+q1)is a nondecreasing function of t,then we have

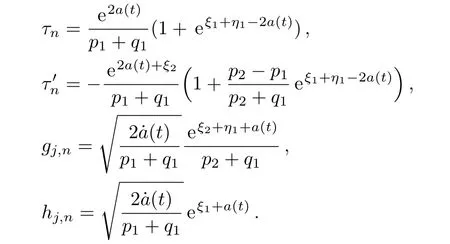
Therefore,the one-soliton solution of the nonlinear modified differential-difference KP equation with self-consistent sources(45)–(48)is given by

Fig.1 The shape and motion of the one-soliton solution Wnfor a(t)=0.2e2t:(a)t=0.2,(b)t=1.2.

Fig.2 The shape and motion of the one-soliton solution Wnfor a(t)=0.1(t+cost):(a)t=0.2,(b)t=1.2.

In order to get a non-trivial and non-singular solution,we set p1>p2>0,q1< −p2<0,p1+q1≠0 in Eqs.(51)–(54).Equations(51)and(52)provide line solitons traveling with constant amplitudes

the top traces

and

which are straight lines with the same slope−ln((1+p1)/(1−q1))/(p1+q1)in the n,y plane,respectively.The corresponding sources are given by Eqs.(53)and(54).The source,whose role is played by a(t),changes the top traces or velocities of the solitons(51)–(52)but not their shapes.Figures 1–4 show the shapes and motions of the one-soliton solution Wn,Ungievn in(51)–(52)by taking p1=0.6,p2=0.4,q1= −0.8,=0 for different choices of a(t).

Fig.3 The shape and motion of the one-soliton solution Unfor a(t)=0.2e2t:(a)t=0.2,(b)t=1.2.

Fig.4 The shape and motion of the one-soliton solution Unfor a(t)=0.1(t+cost):(a)t=0.2,(b)t=1.2.

If we take K=1,N=2 and

we derive

Substitution of the functions(55)–(58)into the dependent variable transformations(44)gives two-soliton solution of the modified differential-difference KP equation with self-consistent sources(45)–(48).

3 Casorati Determiant Solution for Modified Differential-Difference KP Equation with Self-Consistent Sources

In Sec.2,we obtain the N-soliton solution(24),(29)–(30)expressed in terms of the Grammian determinant to the modified differential-difference KP equation with self-consistent sources(27)–(28),(31)–(32).In this section,we express the N-soliton solution of the modified differential-difference KP equation with self-consistent sources(27)–(28),(31)–(32)in the form of the Casorati determinant and clarify its bilinear structure.

Proposition 2The modified differential-difference KP equation with self-consistent sources(27)–(28),(31)–(32)has the following Casorati determinant solution:

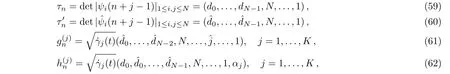
where

in which ϕi1(n+m),ϕi2(n+m)for m=0,...,N;i=1,...,N are functions of n,y,t and

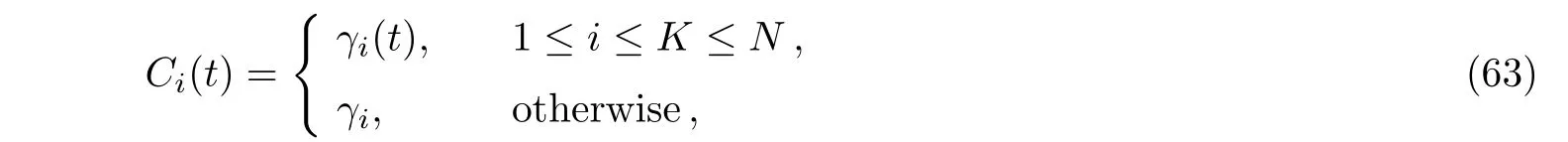
with γi(t)being an arbitrary function of t and K,N being positive integers.In addition, ϕi1(n),ϕi2(n)satisfy the following dispersion relations:

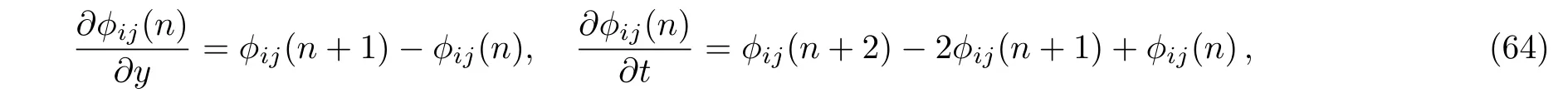
for j=1,2,and the pfaffian elements are defined by

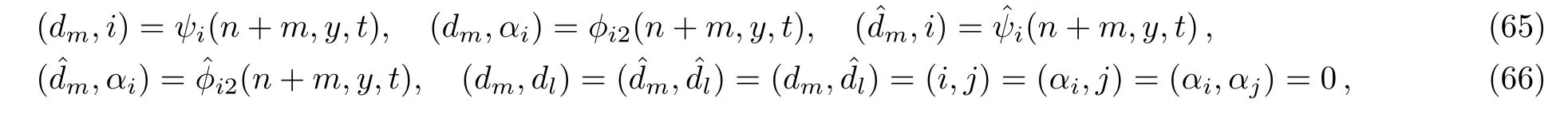
in which i,j=1,...,N and m,l are integers.

ProofWe can drive the following dispersion relation forfrom the Eqs.(64):

We can calculate the following differential and difference formula for Casorati determinants(59)–(62)by applying properties of the determinant and dispersion relations(67)–(69):

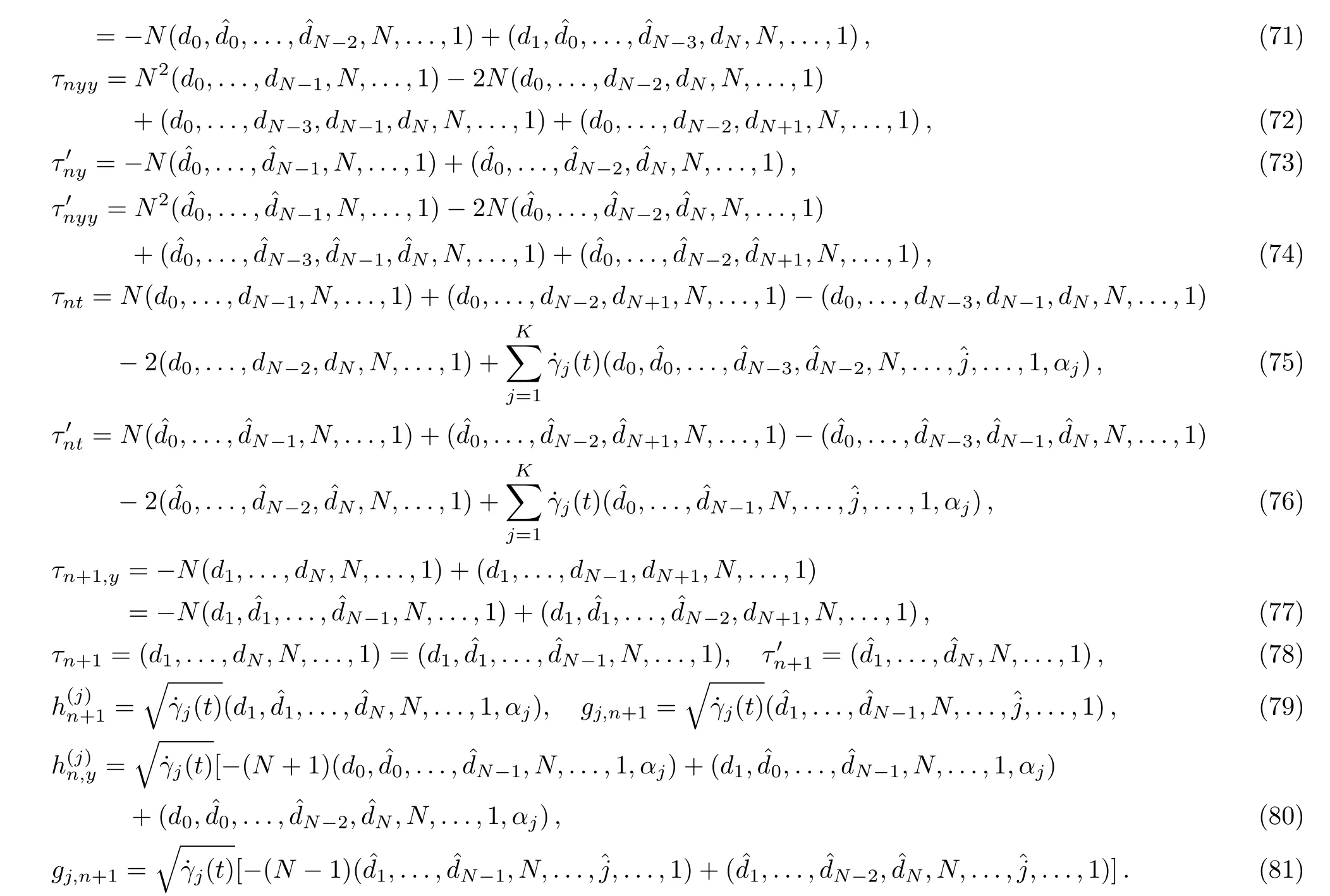
By substituting the expressions(72)–(81),the modified differential-difference KP equation with self-consistent sources(27)–(28),(31)–(32)reduces to the following pfaffian identities:

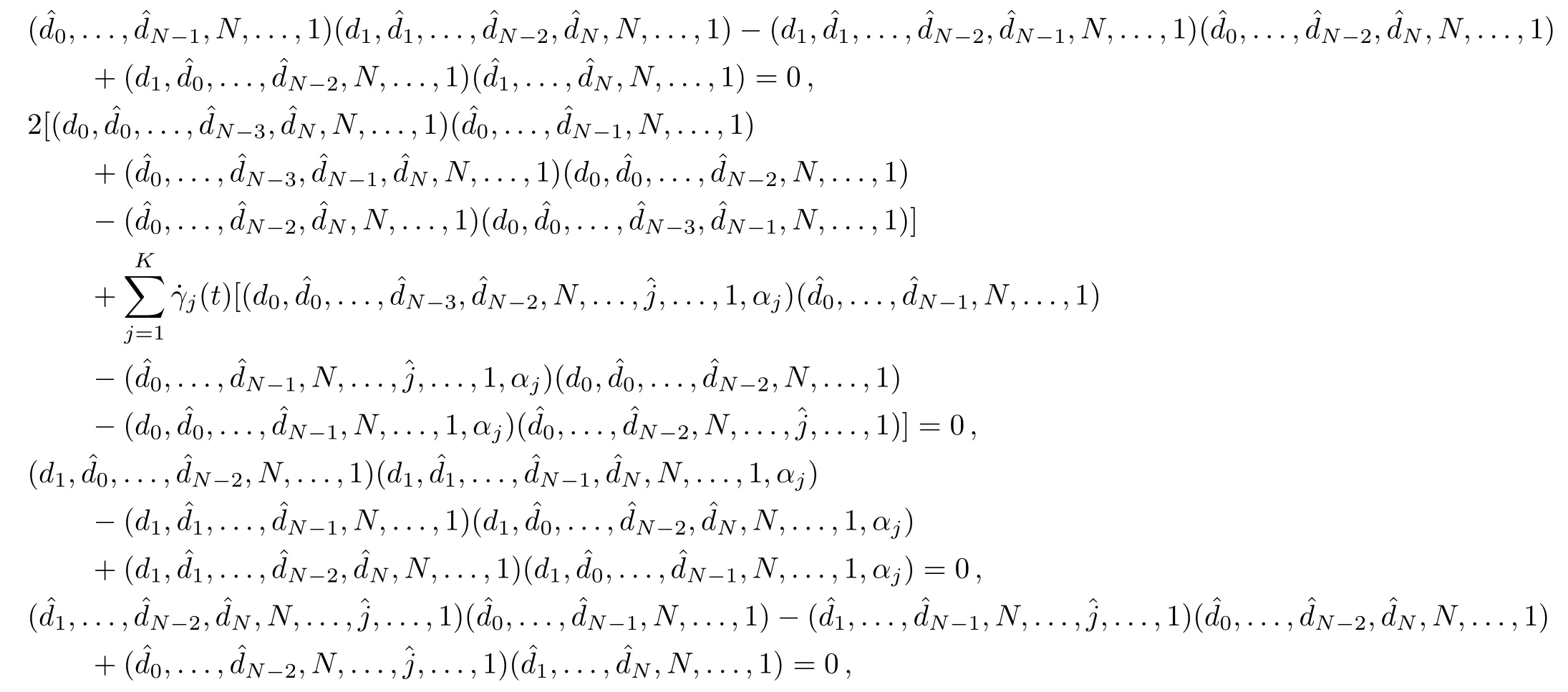
respectively.

4 Commutativity of Source Generation Procedure and Bäcklund Transformation

In this section,we derive another form of the modified differential-difference KP equation with self-consistent sources,which is a Bäcklund transformation for the differential-difference KP equation with self-consistent sources given in Ref.[31].This shows that the commutativity of the source generation procedure and Bäcklund transformation is valid for the differential-difference KP equation.

We have shown that the Casorati determinants τn,(j=1,...,K)given in Eqs.(59)–(62)satisfy the modified differential-difference KP equation with self-consistent sources(27)–(28),(31)–(32).Now we take

for j=1,...,K,and introduce two new fields

where the pfaffian elements are defined in Eqs.(65)–(66).It is not difficult to show that Casorati determinants Fn,(j=1,...,K)and(j=1,...,K)are two solutions to the differential-difference KP equation with self-consistent sources derived in Ref.[31]:

Furthermore,we can verify that the Casorati determinants Fn,(j=1,...,K)given in Eqs.(82)–(87)satisfy the following bilinear equations:

which is another form of the modified differential-difference KP equation with self-consistent sources.

It is proved in Ref.[31]that the differential-difference KP equation with self-consistent sources(88)–(90)possess the following bilinear Bäcklund transformation:

If we take λ =1,θ= −1,ν =0,µj=1,j=1,...,K in Eqs.(97)–(102),we obtain the modified differential-difference KP equation with self-consistent sources(91)–(96).Therefore,the commutativity of source generation procedure and Bäcklund transformation is valid for the modified differential-difference KP equation.

5 Conclution and Discussion

In this paper,we show that Vn=Wn−Unis a Miura transformation connecting the solutions of differential-difference KP equation(1)and the modified differential-difference KP equations(12)–(13).We present the Grammian solution to the modified differential-difference KP equations(12)–(13)from which we construct an integrable coupled modified differential-difference KP system(45)–(48)employing the source generation procedure.By expressing its N-soliton solution in terms of the Grammian and Casorati determinants,the bilinear modified differential-difference KP equation with self-consistent sources(27)–(28),(31)–(32)is resolved into the determinant identities.Another form of the modified differential-difference KP equation with self-consistent sources(91)–(96)which constitutes a Bäcklund transformation for the differential-difference KP equation with self-consistent sources is generated and solved via the source generation procedure.

Now we investigate a continuum limit of the modified differential-difference KP with self-consistent sources(27)–(28),(31)–(32).If we take

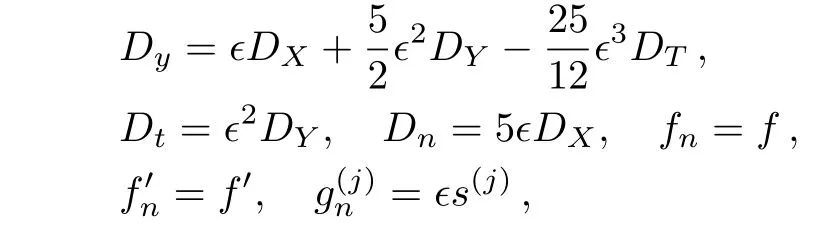
in(10),(28),(31)–(32)and compare ϵ3order in Eq.(10)and ϵ2order in Eqs.(28),(31)–(32),we obtain the mKP equation with self-consistent sources:

Recently,the integrable nonlocal nonlinear equations with PT-symmetry have attracted the great interests of researchers.[32−36]It is interesting for us to generalize the source generation procedure to those nonlocal nonlinear equations.

Acknowledgements

The authors would like to express their sincere thanks to the referees for valuable suggestions.

[1]J.Leon and A.Lati fi,J.Phys.A 23(1990)1385.

[2]V.K.Mel’nikov,Commun.Math.Phys.112(1987)639.

[3]V.K.Mel’nikov,Commun.Math.Phys.126(1989)201.

[4]V.K.Mel’nikov,Lett.Math.Phys.7(1983)129.

[5]V.K.Mel’nikov,Inverse Problems 6(1990)233.

[6]V.K.Mel’nikov,Inverse Problems 8(1992)133.

[7]Y.B.Zeng,W.X.Ma,and R.L.Lin,J.Math.Phys.41(2000)5453.

[8]R.L.Lin,Y.B.Zeng,and W.X.Ma,Physica A 291(2001)287.

[9]Y.B.Zeng,W.X.Ma,and Y.J.Shao,J.Math.Phys.42(2001)2113.

[10]Y.B.Zeng,Y.J.Shao,and W.X.Ma,Commun.Theor.Phys.38(2002)641.

[11]T.Xiao and Y.B.Zeng,J.Phys.A:Math.Gen.37(2004)7143.

[12]X.J.Liu and Y.B.Zeng,J.Phys.A:Math.Gen.38(2005)8951.

[13]Y.B.Zeng,Y.J.Shao,and W.M.Xue,J.Phys.A:Math Gen.36(2003)5035.

[14]W.X.Ma,Chaos,Solitons and Fractals 26(2005)1453.

[15]Y.Hase,R.Hirota,Y.Ohta,and J.Satsuma,J.Phys.Soc.Jpn.58(1989)2713.

[16]Y.Matsuno,J.Phys.A:Math.Gen.24(1991)L273.

[17]X.B.Hu,J.Phys.A:Math.Gen.24(1991)5489.

[18]D.J.Zhang,J.Phys.Soc.Jpn.71(2002)2649.

[19]H.H.Hao,D.J.Zhang,and S.F.Deng,Theor.Math.Phys.158(2009)151.

[20]D.J.Zhang and H.Wu,Commun.Theor.Phys.49(2008)809.

[21]Gegenhasi and X.B.Hu,J.Nonlinear Math.Phys.13(2006)183.

[22]O.Chvartatskyi,A.Dimakis,and F.Müller-Hoissen,Lett.Math.Phys.106(2016)1139.

[23]F.Müller-Hoissen,O.Chvartatskyi,and K.Todac,J.Geom.Phys.113(2017)226.

[24]X.B.Hu and H.Y.Wang,Inverse Problems 22(2006)1903.

[25]E.Date,M.Jimbo,and T.Miwa,J.Phys.Soc.Jpn.51(1982)4125.

[26]T.Tamizhmani,S.K.Vel,and K.M.Tamizhmani,J.Phys.A:Math.Gen.31(1998)7627.

[27]R.Hirota,Direct Methods in Soliton Theory,Cambridge University Press,Cambridge(2004).

[28]J.X.Zhao,Gegenhasi,and Xing-Biao Hu,J.Phys.Soc.Jpn.78(2009)064005.

[29]M.Jimbo and T.Miwa,Publ.RIMS,Kyoto Univ.19(1983)943.

[30]F.Gesztesy and W.Schweiger,Rep.Math.Phys.30(1991)205.

[31]Gegenhasi and X.B.Hu,Math.Comput.Simulat.74(2007)145.

[32]M.J.Ablowitz and Z.H.Musslimani,Phys.Rev.Lett.110(2013)064105.

[33]M.J.Ablowitz and Z.H.Musslimani,Phys.Rev.E 90(2014)032912.

[34]M.J.Ablowitz and Z.H.Musslimani,Nonlinearity 29(2016)915.

[35]A.S.Fokas,Nonlinearity 29(2016)319.

[36]M.J.Ablowitz and Z.H.Musslimani,Stud.Appl.Math.139(2017)7.