Melting Heat in Radiative Flow of Carbon Nanotubes with Homogeneous-Heterogeneous Reactions

Tasawar Hayat,Khursheed Muhammad,Taseer Muhammad,,3,∗and Ahmed Alsaedi

1Department of Mathematics,Quaid-I-Azam University,Islamabad 44000,Pakistan

2Nonlinear Analysis and Applied Mathematics(NAAM)Research Group,Department of Mathematics,Faculty of Science,King Abdulaziz University,Jeddah 21589,Saudi Arabia

3Department of Mathematics,Government College Women University,Sialkot 51310,Pakistan

Nomenclature

?

1 Introduction

Presently improvement of thermal engineering and industrialization displays a directly relation to develop more productive and conservative heat transfer framework.Thus many attempts have been made for an enhancement of heat transfer rate by different equipments and liquids.[1−7]The themal conductance of solid particles is more than the liquids.By addition of these small sized particles,the themal conductance of liquids can be improved.These particles are known as nanoparticles.The thermal conductance of the poor conducting liquids like kerosine oil,ethylene glycol,water,gasoline oil etc.highly varies with the shape of nanomaterials.Cylindrical nanomaterials have better performance in order to improve the thermal conductance of poor thermal liquids.[8]Carbon nanotubes are also utilized as nanomaterials.Basically carbon nanotubes are tube shaped materials ranging size between 1nm and 50 nm.On the basis of structure,the carbon nanotubes are of two kinds.Carbon nanotubes with single graphene layer is single-wall while with more than one layer is known as multi-wall carbon nanotubes.There are widespread applications of CNTs in filtration of water,bulletproof jackets,batteries,solar storage and semicoductors etc.Choi[9]was the first who utilized the nanomaterials.Further some recent studies in this regard can be seen in the investigations.[10−16]

Melting and solidification play a key part in the present and progressed mechanical procedures.Scientist and researchers are intrigued to investigate melting heat transfer because of extensive variety of uses of melting/solidifying phenomenon of solid-liquid phase change materials in the process of welding,freeze treatment of sewage,development of crystals,stocking of thermal energy,optimum usage of energy,solidification of magma and production of semiconductors.By placing semi in finite body of ice in the steam of hot air,melting was inspected by Robert.[17]Some related attempts in this area can be seen through the studies.[18−22]

Reactions are classified into homogeneous and heterogeneous types.This qualification is connected to the way that catalyst operates in a similar phase(homogeneous)or in various phase(heterogeneous).Generally both homogeneous and heterogenous reactions have significance in numerous chemical reacting frameworks.Impact of chemical reactions is particularly critical in assembling of ceramics,polymer creation,metallurgy and hydrometallurgical industry,chemical handling hardware plan and crops harm by means of solidifying,food processing,biochemical frameworks,combustion,catalysis,refining process,hydro-metallurgical gadgets and numerous others.The related work according to the literature survey is presented in the attempts.[23−27]

Motivated by the aforementioned applications of carbon nanotubes(CNTs),the underlying objective of this attempt is to develop a mathematical model for stagnation-point flow of carbon nanotubes with homogeneous-heterogeneous reactions. Melting heat transfer and thermal radiation effects are also considered.Thermal conductivity of carbon nanotubes is estimated through the well known Xue model.Such research work is not carried out in the past even in the absence of melting heat transfer.Researchers also found that dispersion of carbon nanotubes in water elevates the thermal conductivity of resulting nanofluid by 100%.[10]Both singlewalled carbon nanotubes(SWCNTs)and multi-walled carbon nanotubes(MWCNTs)are considered.Behaviors of velocity,temperature,skin friction coefficient,and local Nusselt number are presented graphically.Optimal values of convergence control parameters are obtained by optimal homotopy analysis method(OHAM).Graphical results are presented and analyzed.

2 Formulation

We consider the steady 2D stagnation-point flow towards a nonlinear stretchable surface with chemical reactions.Heat transfer is studied via melting heat and thermal radiation.Concept of carbon nanotubes is employed.Sheet thickness is considered by y=B(x+b)(1−m∗)/2,which varies with the distance from the slot due to acceleration/deceleration.CNTs(single-wall CNTs and multiwall CNTs)are utilized in water and gasoline oil.Cartesian coordinates are chosen in the problem formulation.The homogeneous reaction for cubic autocatalysis is given by

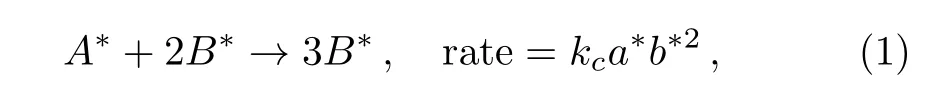
while isothermal reaction of order first on the catalyst surface is

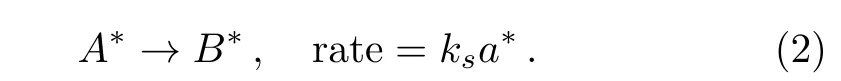
These expressions of reactions guarantee that the rate of reaction is zero in external flow as well on the outer edge of boundary layer.After utilizing boundary layer approximations,we have the following systems:[14,21]

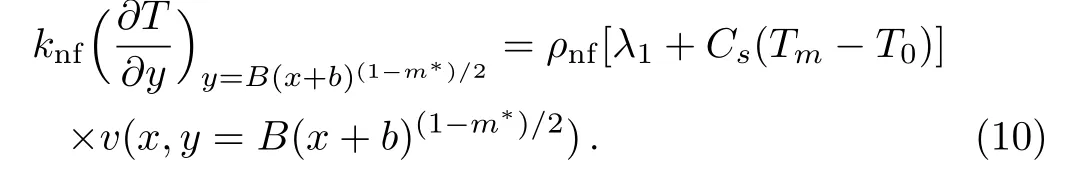
The shape of the surface is highly dependent upon m∗.For m∗=1,the surface became flat while for m∗<1 thickness of the surface increases due to which the surface became outer convex.For m∗>1 the thickness of the wall decreases,which is responsible for the inner concave like shape of surface.The condition of melting heat transfer is Xue[28]elaborated that earlier nanofluid models are only valid for rotational or spherical elliptical materials with very small axial ratio.On the basis of thermal conductivity space distribution,the properties of carbon nanotubes cannot be described by these models.To overcome this void,a theoretical model[28]by Maxwell theory for elliptically rotational nanotubes having larger axial ratio and balancing the impacts of space distribution on carbon nanotubes is given by

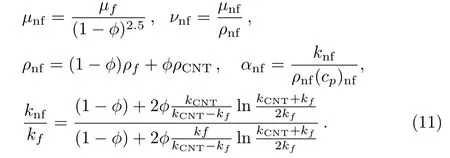
Density,specific heat and thermal conductivity of base liquids(water and gasoline oil)and nanomaterials are given in Table 1.

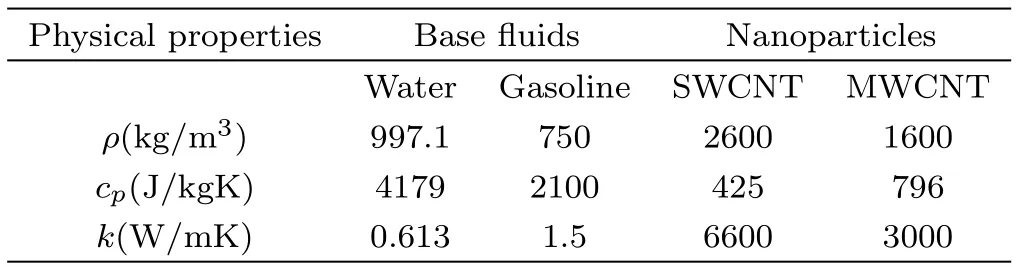
Table 1 Numerical data of density,specific heat and thermal conductivity for base fluids and carbon nanotubes.[28]

Transformations are defined as follows:

Continuity equation is trivially satis fied and Eqs.(4)–(11)yield

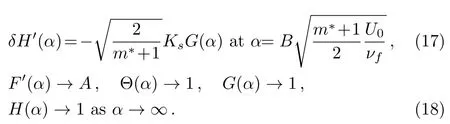
Assuming that both DAand DBare equal i.e.,δ=1:[23]

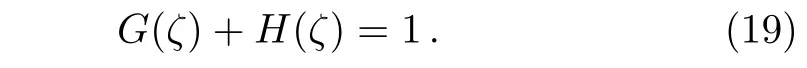
Equations(15)and(16)yield

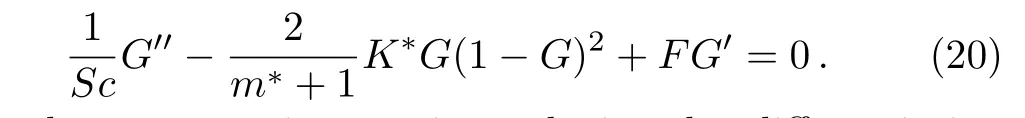
In above expressions,primes depict the differentiation with respect to ζ,

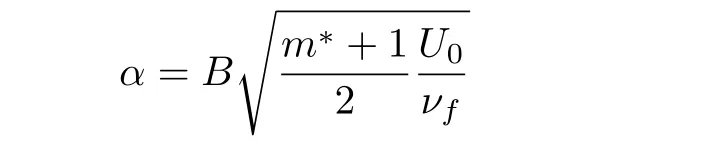
the wall thickness parameter and

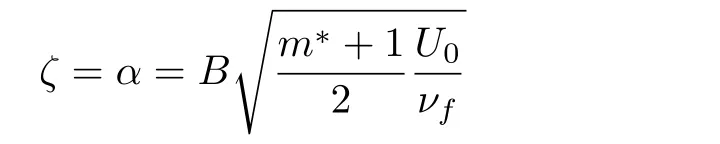
the flat surface.We define F(ζ)=f(ζ− α)=f(η),Θ(ζ)= θ(ζ− α)= θ(η),and G(ζ)=g(ζ− α)=g(η).Therefore Eqs.(13)–(20)become

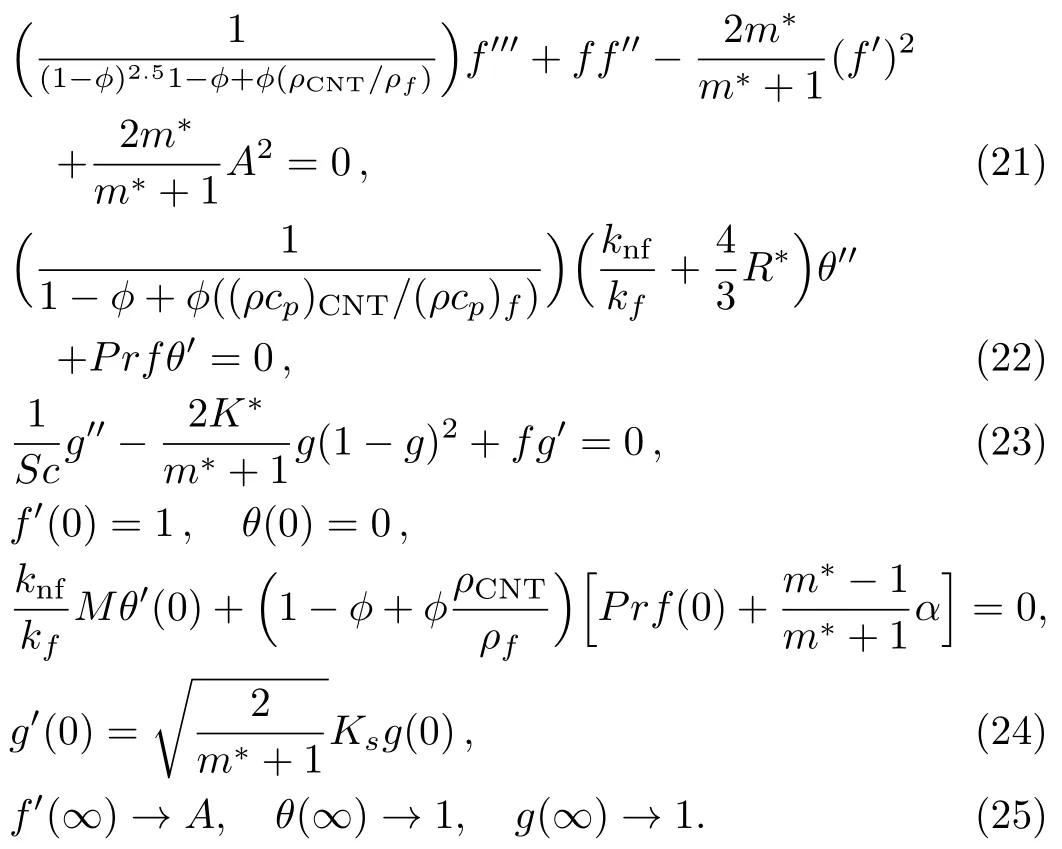
The definitions of above physical parameters are given below:

Skin friction coefficient and local Nusselt number are

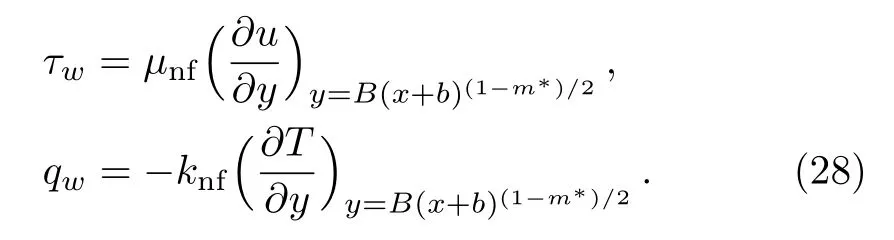
with Dimensionless forms of skin friction coefficient and local Nusselt number are

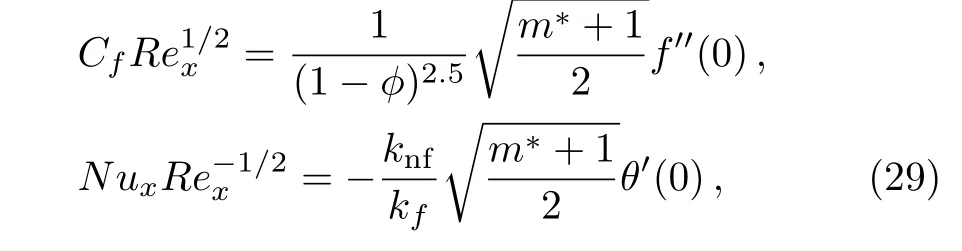
where Rex=Uw(x+b)/νfis the local Reynolds number.

3 Solution by BVPh2.0

The obtained system of nonlinear ODEs is solved by Optimal HAM.[29]Initial guesses and linear operators are:[30−32]

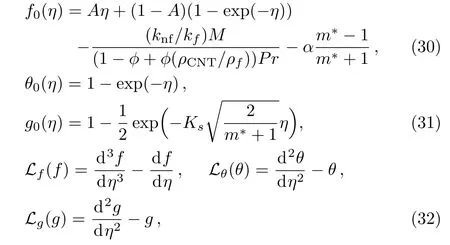
with

where Ej(j=1–7)denotes the arbitrary constants.

4 Convergence Analysis

Here hf,hθ,and hgfor single and multi-wall CNTs by considering water and gasoline oil as base liquids are evaluated by BVPh2.0.We have solved the momentum,energy and concentration equations via BVPh2.0.Such equations consist of unknown parameters hf,hθ,and hg.Taking minimum total error,the optimal values of these parameter can be computed.In the frame of HAM.These parameters play a vital role.That is why these parameters are refered to as convergence-controll parameter,which differs HAM from other analytical approximation methods.In order to highly reduce the CPU time,we used average residual error at the k-th older of approximation defined by

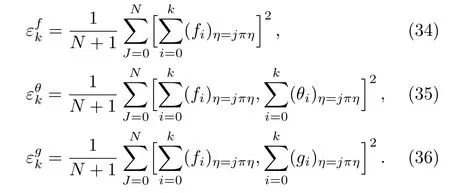
The optimal values for parameters in SWCNT-water are hf=−0.354 50,hθ=−0.103 09,and hg=−0.306 56 and for gasoline oil are hf= −0.969 61,hθ= −0.099 19 and hg=−0.311 19 while optimal values for MWCNT-water are hf= −0.350 83,hθ= −0.107 85,hg=−0.304 78 and for gasoline oil are hf= −0.682 57,hθ= −0.101 64,and hg=−0.309 69.In Fig.1,the total residual error verses order of approximation is presented for both single and multi-wall CNTs considering water and gasoline as base liquids.Table 2 presents average square residual error at different order of approximations for both water and gasoline oil.

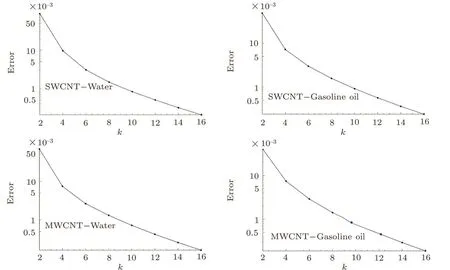
Fig.1 Error with order of approximations.

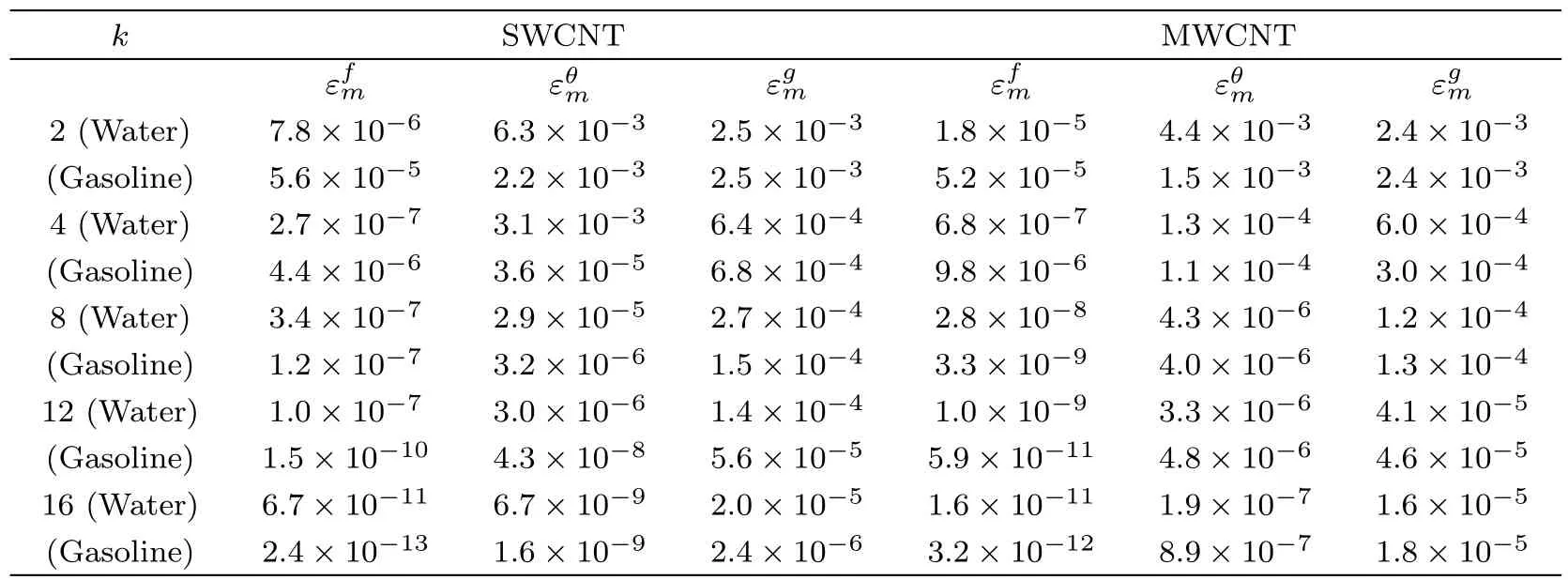
Table 2 Individual average square residual error using optimal data of auxilary variables.

5 Discussion

In this section,the velocity,temperature,concentration,skin friction coefficient and local Nusselt number have been discussed under the influential variables for two cases i.e.,single and multi-wall CNTs in the presence of water and gasoline oil.Figures 2–6 are visualized for the behavior of velocity towards ϕ,M,m∗,A,and α.It is inspected that velocity of fluid shows rapid growth for higher values of ϕ,M,A,m∗≥ 1 and α while opposite impact is studied for larger m∗≤1.For velocity field,the impact of multi-wall CNTs dominantes over single-wall CNTs for larger ϕ and m∗in case of both water and gasoline oil.

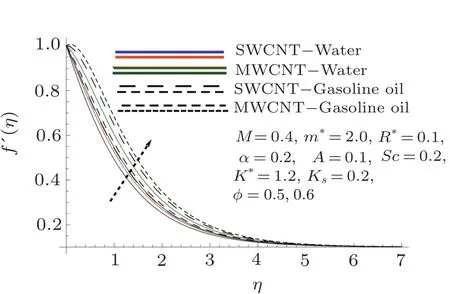
Fig.2 Curves of f′via ϕ.

Fig.3 Curves of f′via M.

Similarly for larger M,A and α,the influence of singlewall CNTs dominants over multi-wall CNTs in velocity field.It is due to the fact that for higher M,the rapid moment of heated fluid towards melting surface occurs due to which velocity enhances.It is also founded that velocity is higher for larger A in both cases i.e.,A>1 and A<1.Furthermore boundary layer has opposite trend for A>1 and A<1 but there in no development of boundary layer for A=1 in case of both water and gasoline oil.

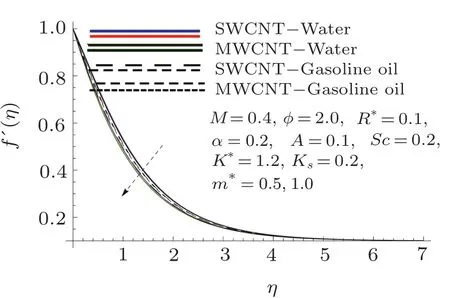
Fig.4 Curves of f′via m∗.

Temperature under the impact of M,A,and R∗is composed in Figs.7–9.It is observed that temperature of fluid declines for higher M,A,and R∗.

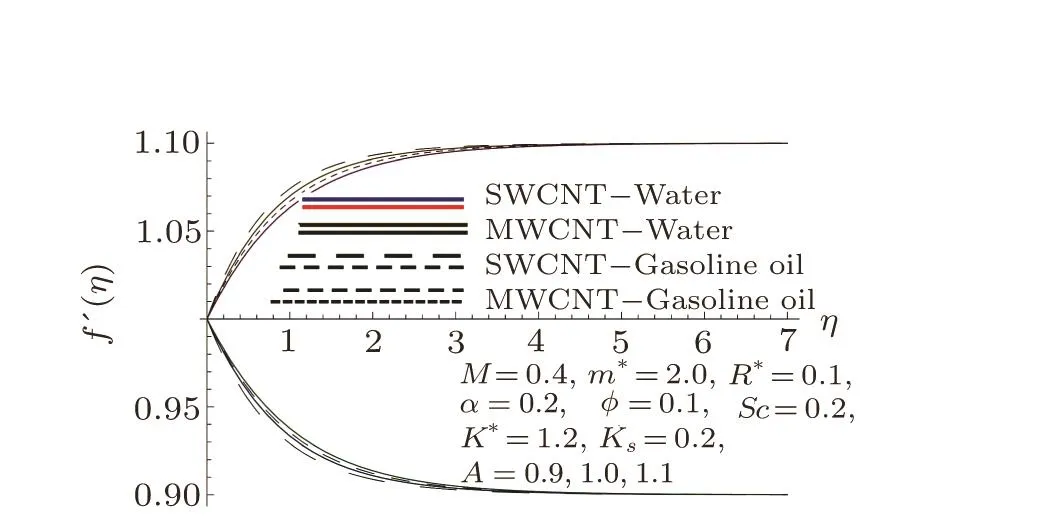
Fig.5 Curves of f′via A.

Impact of single-wall CNTs dominants over multi-wall CNTs.For higher M,the flow of heated fluid towards cooled surface increases,and thus velocity of fluid enhances and is responsible for the decline of temperature of the fluid.Moreover thermal boundary layer enhances for higher M.For higher A,the temperature of fluid decays.It is because larger A is responsible for higher pressure and resistance to the flow reduces.Hence temperature of the fluid increases.

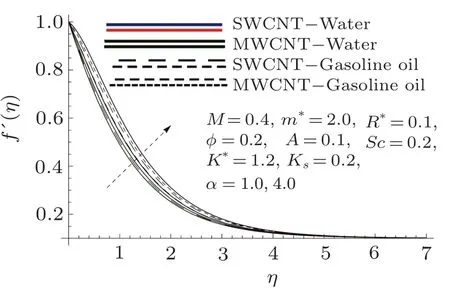
Fig.6 Curves of f′via α.

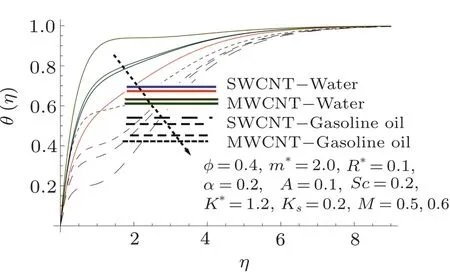
Fig.7 Curves of θ via M.

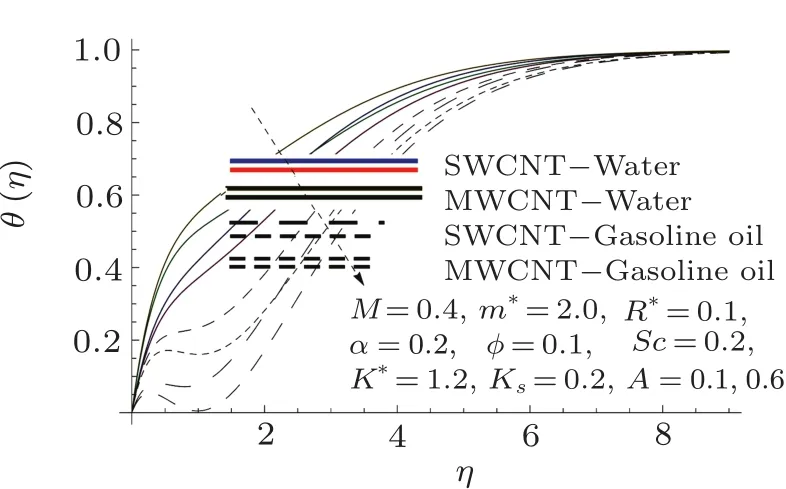
Fig.8 Curves of θ via A.

Effects of K∗,Ksand Sc on concentration are markedout in Figs.10–12.It is founded that there is intensi fication in the concentration pro file for higher Ksand Sc while opposite behavior is inspected for larger K∗.Also solutal boundary layer enhances for larger K∗.It is examined that influence of multi-wall CNTs is more efficient than that of single-wall CNTs in both water and gasoline oil.The ratio of momentum diffusivity to mass diffusivity is called Schmidt number.

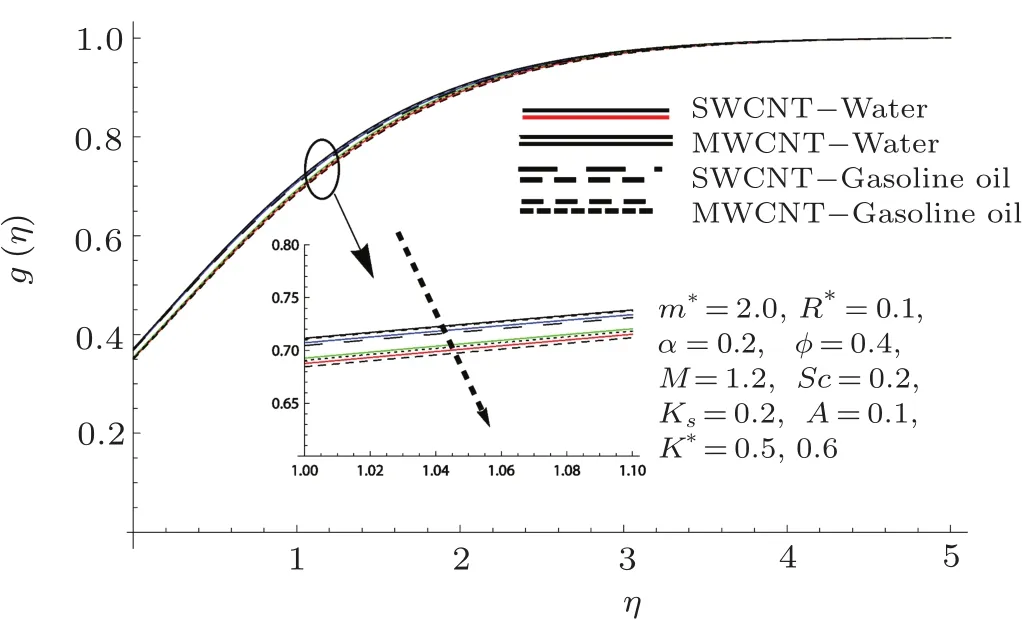
Fig.10 Curves of g via K∗.

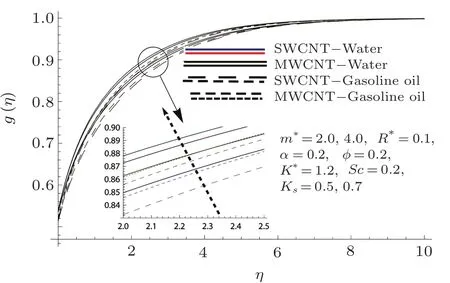
Fig.11 Curves of g via Ks.

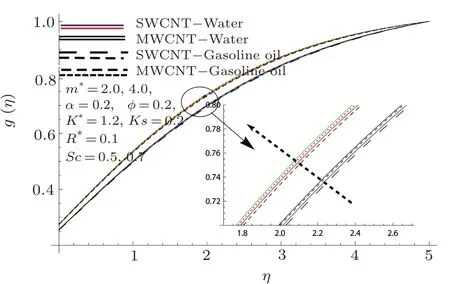
Fig.12 Curves of g via Sc.

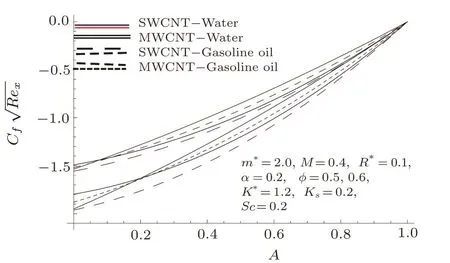
Fig.13 Curves ofvia A and ϕ.

Fig.14 Curves of CfRe1/2x via m∗and M.

Fig.15 Curves of NuxRe−1/2x via ϕ and M.

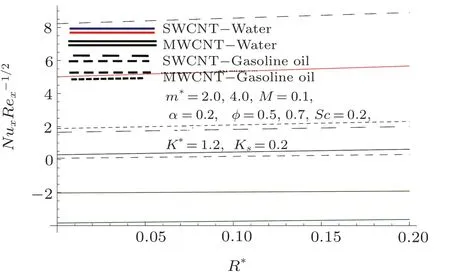
Fig.16 Curves of NuxRe−1/2x via R∗ and ϕ.

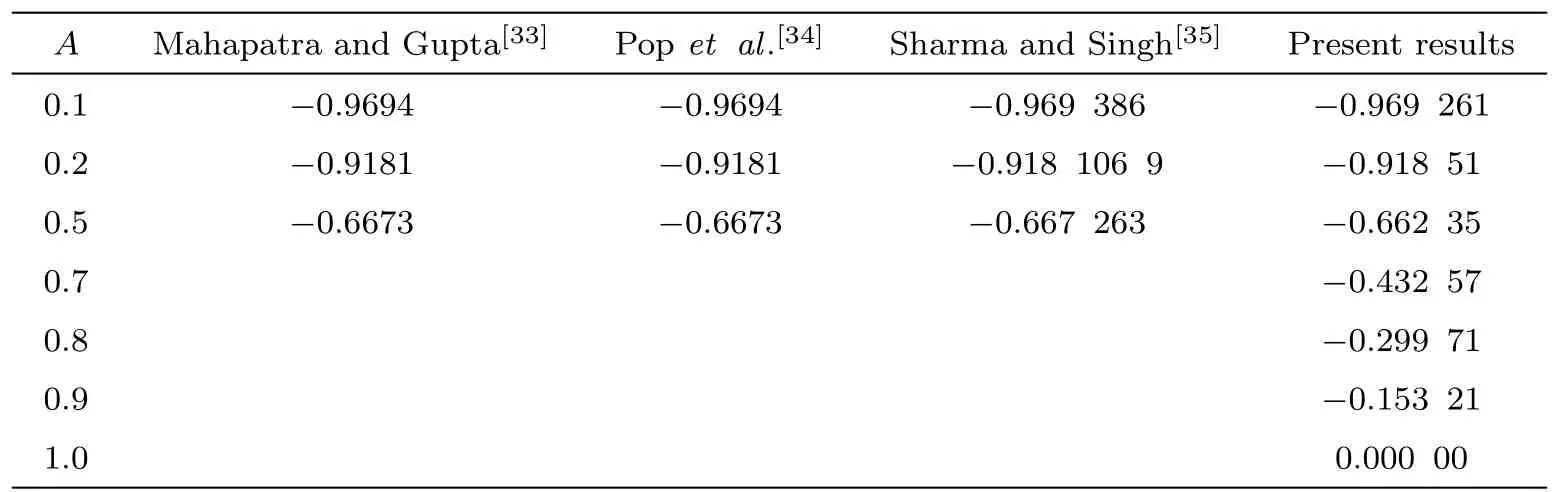
Table 3 Comparative values of CfRe1/2x for different values of A when m∗ =1 and ϕ =0.

Thus due to increment in Sc,the mass diffusivity reduces which causes decline in concentration pro file.Skin friction coefficient under the impact of A,ϕ,M,and m∗are traced in Figs.13 and 14.Here skin friction coefficient rises for higher M and A while it decreases for larger ϕ and m∗.Impacts of ϕ,M,and R∗on local Nusselt number are depicted in Figs.15 and 16.Rate of heat transfer is higher for larger values of mentioned parameters.Also the impact of single-wall CNTs dominantes over multi-wall CNTs by considering parameters ϕ and M while considering ϕ and R∗the impact of multi-wall CNTs is efficient in term of heat transfer.Table 3 is developed to validate the present results with the previously published results in a limiting sense.From this Table,we analyzed that the present OHAM solutions have good agreement with the previous numerical solutions in a limiting sense.

6 Conclusions

In the present work,we have discussed melting heat transfer and thermal radiation effects in stagnation-pointflow of carbon nanotubes towards a nonlinear stretchable surface with variable thickness.The final outcomes are listed below.

• Velocity enhances for larger M and α.Also the impact of single-wall CNTs is efficient than that of multi-wall CNTs in both water and gasoline oil cases.

• For higher values of ϕ,the velocity of fluid shows rapid growth while for larger m∗,the opposite trend is noticed.Impact of multi-wall CNTs is greater than single wall CNTs.

•Temperature pro file decreases with an increment in M,A,and R∗.Single-wall CNTs show greater impact than multi-wall CNTs in both water and oil cases.

•Concentration pro file shows an enlargement with an increase in Sc and Kswhile reduction is noticed for higher

•For higher values of ϕ and m∗,a reduction in skin friction coefficient for both single-wall CNTs and multiwall CNTs is observed while opposite behavior is studied for larger A and M.

•Local Nusselt number is increased for larger values of ϕ and R∗.Influence of multi-wall CNTs is more efficient when compared with single-wall CNTs.

[1]T.Hayat,T.Muhammad,A.Alsaedi,and M.S.Alhuthali,J.Magn.Magn.Mater.385(2015)222.

[2]M.M.Bhatti and M.M.Rashidi,J.Mol.Liq.221(2016)567.

[3]M.M.Bhatti and M.M.Rashidi,J.Nanofluids 5(2016)543.

[4]S.R.Mishra,P.K.Pattnaik,M.M.Bhatti,and T.Abbas,Indian J.Phys.91(2017)1219.

[5]S.R.Mishra and M.M.Bhatti,Chin.J.Chem.Eng.25(2017)1137.

[6]M.M.Bhatti,M.Shiekholeslami,and A.Zeeshan,Entropy 19(2017)481.

[7]M.M.Bhatti,M.A.Abbas,and M.M.Rashidi,Appl.Math.Comp.316(2018)381.

[8]M.F.L.D.Volder,S.H.Taw fick,R.H.Baughman,and A.J.Hart,Science 339(2013)535.

[9]S.U.S.Choi,American Society of Mechanical Engineers(ASME),FED 231/MD(1995)99.

[10]S.U.S.Choi,Z.G.Zhang,W.Yu,et al.,Appl.Phys.Lett.79(2001)2252.

[11]M.Turkyilmazoglu,Eur.J.Mech.B/Fluids 53(2015)272.

[12]M.Shiekholeslami and R.Ellahi,Int.J.Heat Mass Tran.89(2015)799.

[13]T.Hayat,K.Muhammad,M.Farooq,and A.Alsaedi,Plos One 11(2016)e0152923.

[14]T.Hayat,S.Ahmed,T.Muhammad,and A.Alsaedi,Physica E 94(2017)70.

[15]S.Soltani,A.Kasaeian,H.Sarrafha,and D.Wen,Solar Energy 155(2017)1033.

[16]T.Hayat,K.Ra fique,T.Muhammad,et al.,Results Phys.8(2018)26.

[17]L.Roberts,J.Fluid Mech.4(1958)505.

[18]N.Bachok,A.Ishak,and I.Pop,Phys.Lett.A 374(2010)4075.

[19]N.A.Yacob,A.Ishak,and I.Pop,Comp.Fluids 47(2011)16.

[20]T.Hayat,M.Farooq,and A.Alsaedi,Int.J.Numer.Methods Heat Fluid Flow 24(2014)760.

[21]T.Hayat,K.Muhammad,M.Farooq,and A.Alsaedi,AIP Adv.6(2016)015214.

[22]R.S.Saif,T.Hayat,R.Ellahi,et al.,Results Phys.7(2017)2821.

[23]J.H.Merkin,Math.Comp.Model.24(1996)125.

[24]P.K.Kameswarn,S.Shaw,P.Sibanda,and P.V.S.N.Murthy,Int.J.Heat Mass Tran.57(2013)465.

[25]T.Hayat,M.Farooq,and A.Alsaedi,AIP Adv.5(2015)027130.

[26]M.I.Khan,T.Hayat,M.I.Khan,and A.Alsaed,Int.J.Heat Mass Tran.113(2017)310.

[27]T.Hayat T.Ayub,T.Muhammad,and A.Alsaedi,Results Phys.7(2017)2812.

[28]Q.Xue,Physica B 368(2005)302.

[29]U.Farooq,Y.L.Zhao,T.Hayat,and S.J.Liao,Comp.Fluids 111(2015)64.

[30]S.J.Liao,Commun.Nonlinear Sci.Numer.Simul.15(2010)2003.

[31]T.Hayat,K.Muhammad,M.Farooq,and A.Alsaedi,J.Mol.Liq.220(2016)216.

[32]T.Hayat,A.Aziz,T.Muhammad,and A.Alsaedi,Commun.Theor.Phys.68(2017)387.

[33]T.R.Mahapatra and A.Gupta,Heat and Mass Transfer 38(2002)517.

[34]S.Pop,T.Grosan,andI.Pop,TECHNISCHE MECHANIK 25(2004)100.

[35]P.Sharma and G.Singh,J.Appl.Fluid Mech.2(2009)13.