Direct Urca Processes Involving Proton1S0Superfluidity in Neutron Star Cooling∗

Yan Xu(许妍), Zi Yu(喻孜),Xiao-Jun Zhang(张晓军),Cun-Bo Fan(范存波),

Guang-Zhou Liu(刘广洲),3En-Guang Zhao(赵恩广),4Xiu-Lin Huang(黄修林),1,‡ and Cheng-Zhi Liu(刘承志)1,§

1Changchun Observatory,National Astronomical Observatories,CAS,Changchun 130117,China

2College of Science,Nanjing Forestry University,Nanjing 210037,China

3Center for Theoretical Physics,Jilin University,Changchun 130023,China

4Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China

1 Introduction

Neutron star(NS)constitutes one of the best astrophysical laboratories for studying dense matter physics.It arises at the end of life of a(8–20)M⊙massive stars and forms in the aftermath of the core collapse supernovae explosion.A newly born NS is very hot with temperature as high as(1011–1012)K,but rapidly cools to a temperature of less than 1010K within minutes.The cooling process of an NS is dominated by a combination of surface photon emission and interior neutrino emission.The latter is responsible for about(105–106)years until the interior temperature reaches 106K.It is generally known that photon luminosity is obviously lower than neutrino luminosity,meaning that the thermal radiation from an NS surface reflects the intensity of interior neutrino emission.[1−3]While neutrino emisision depends strongly on the composition of superdense matter in NSs.It is well known that NSs cores are dense enough to allow for emerging exotic matter with the strangeness quantum number through weak equilibrium,such as Λ,Σ0,Σ+,Σ−,Ξ0,Ξ−hyperons,referred as npheµmatter,except for the conventional nucleons and leptons(npeµ matter).[4−16]It means that all the possible baryon neutrino emission processes would happen during the neutrino cooling stage.[17−26]Among them,the most powerful enhancement of neutrino emission is provided by the nucleon direct Urca processes,secondarily is the hyperon direct Urca processes.[27−34]Prakash et al.(1992)have already indicated that NS matter with any proton/nucleon ratio can rapidly cool by the baryon direct Urca processes if Λ hyperons are present.[35−36]Besides,the degrees of freedom of hyperons tend to soften the equation of state(EOS)calculated in the relativistic mean field(RMF)model based on SU(6)spin-flavor symmetry(quark model for the vector mesonhyperon coupling constants),then reduce the maximum mass of NS to about(1.6–1.7)M⊙.[37−44]However,Demorest et al.in 2010[45]indicated that the binary millisecond pulsar PSR J1614-2230 expanded the maximum observational mass from 1.67±0.02 M⊙to 1.97±0.04 M⊙using the Shapiro delay measurements from radio timing observations.Antoniadis et al.in 2013[46]observed another massive neutron star PSR J0348+0432,whose mass is 2.01±0.04 M⊙.It is clear that the inclusion of hyperons in such heavy NS cores is difficult to explain by SU(6)spinlf avor symmetry in RMF model.And for this reason,the SU(3)flavor symmetry is widely applied to RMF model.It changes the strength of the isoscalar,vector-meson(ω and ϕ)couplings to the octet states,which can sustain an NS with mass of(1.8–2.1)M⊙even if hyperons exist in NS core.[47−50]Furthermore,baryons in NS interior can become the superfluid state related to the generation of Baryon-Baryon Cooper pairs under attractive interaction.The baryon superfluidity could suppress considerably the baryon direct Urca processes and thus affect the cooling rate of NS remarkably.[5,51]As we all know,the neutrons in the crust and protons,hyperons in the core undergo Cooper pair in1S0state,while neutrons in the core can pair in3P2state.

It is well known that the EOS of hot nuclear matter plays important roles in determining the evolution of the NS at the birth stage,namely a protoneutron star is a finite temperature system.After birth,its neutrinos are trapped due to their short mean free paths.Then,neutrinos quickly diffuse and leave behind much of their energy which causes significant heating of ambient matter.[52−53]Beyond that,the effects of magnetic fields on NS have been a subject of interest from long time ago.The EOS for magnetized matter is important for the NS structure and the cooling of magnetized stars including and not including the anomalous magnetic moments.Moreover,since neutrinos are a fundamental piece in cooling processes,its emission and transport properties in the presence of magnetic fields were studied in detail.The results also show that the possibility for the baryon direct Urca processes to be open in the presence of a magnetic field B,even if the proton fraction is too low to open the process at B=0.[54−57]In this paper,because that we will mainly consider the influence of the hyperons and the hyperon direct Urca processes on the nucleon direct Urca processes and the proton1S0superfluidity in cold neutron star matter.We will further study the influence of temperature,neutrinos and magnetic fields on the properties of the NS cooling in the future work.This paper is arranged as follows.In Sec.2,we make a brief review for RMF and NS cooling theories as well as the gap equation for the proton1S0superfluid.The numerical results are discussed in Sec.3.Finally,we summarize our conclusions in Sec.4.

2 Theoretical Framework

2.1 RMF Theory

In this calculation,we adopt RMF model to describe NS matter.The constituents of NSs fall into two categories:npeµ and npheµ matter.The strong interaction between baryons is mediated by the exchange of isoscalar scalar and vector mesons σ, ω,isovector vector meson ρ.The two additional strange mesons are also included,namely isoscalar scalar σ∗and vector ϕ mesons.[41−42,58]The total Lagrangian is given by

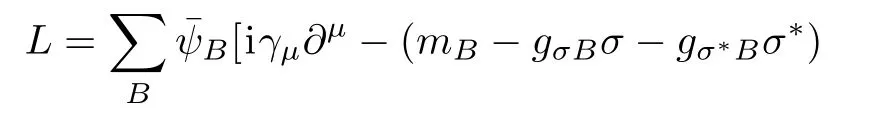
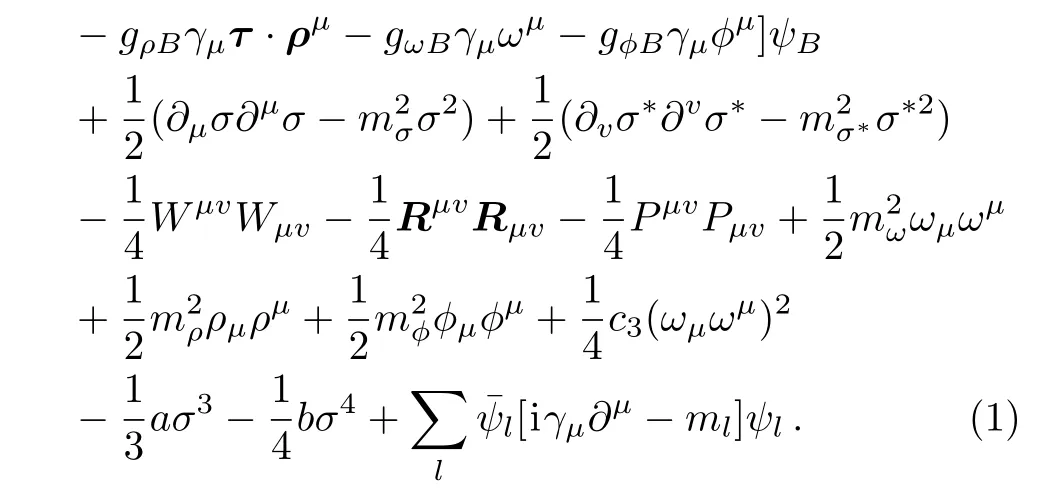
Here Wµv= ∂µωv− ∂vωµ,Rµv= ∂µρv− ∂vρµ,and Pµv= ∂µϕv− ∂vϕµdenote the field tensors of ω,ρ and ϕ mesons,respectively.The sum on B and l runs over the octet baryons and leptons,namely,n,p,Λ,Σ0,Σ+,Σ−,Ξ0,Ξ−,e,µ. ψBand ψlare the Dirac fields of baryons and leptons,respectively.mBand mldenote the masses of baryon and lepton,respectively.γushows the Dirac matrice.The meson fields are replaced by their expectation values at the mean field level.Now we can solve the Euler-Lagrange equations by plugging in the above Lagrangian

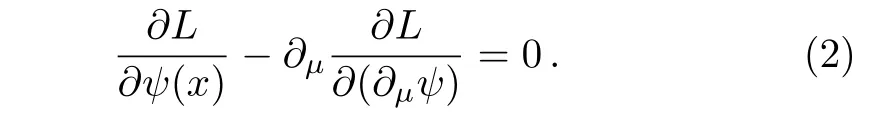
The equations of motion for each baryon and meson fields can be obtained in RMF approximation

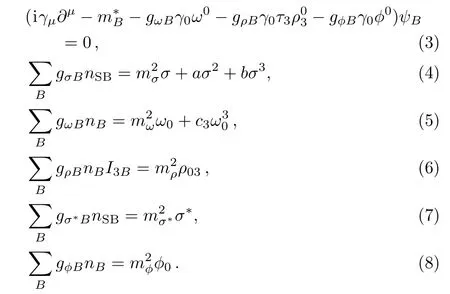
Here JBand I3Bexpress the spin and isospin projections of baryons,respectively.The Dirac effective mass of baryon is given by

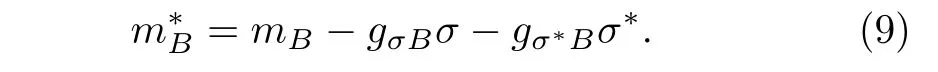
The scalar density nSBand baryon density nBare given by

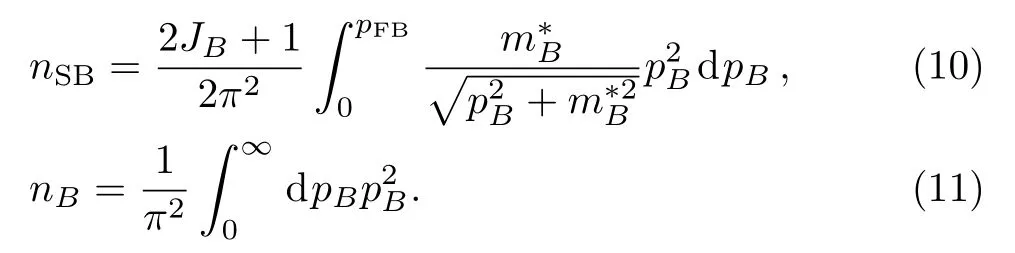
For a fixed total baryon number density

The hadron phase should meet the local charge neutrality and beta-equilibrium conditions.The former is given by

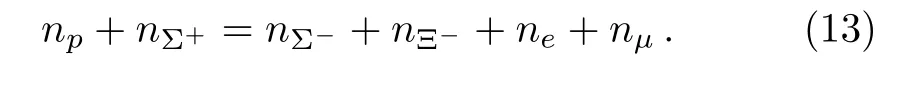
In the latter the chemical potentials of particles are related to each other by,

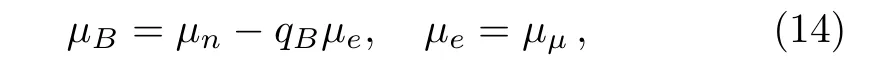
where qBis the electric charge of baryon(in unit of e).

We can solve Eqs.(3)–(14)self-consistently at a fixed total baryon number density nb.The total energy density and pressure of NS matter are

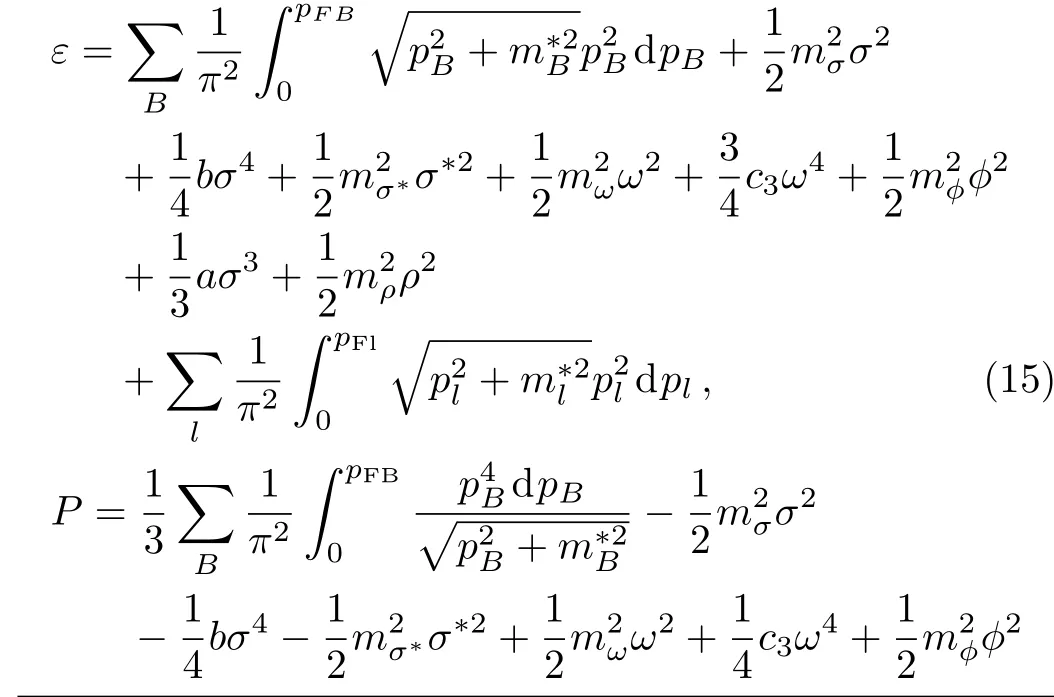
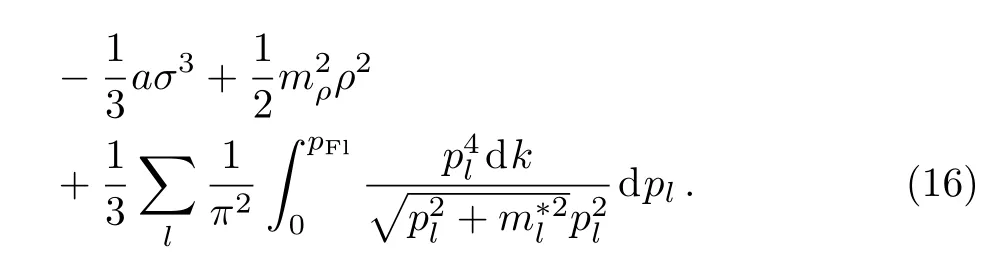
Equations(15)and(16)as inputs,we can obtain the mass-radius relation by solving the Tolman-Oppenheimer-Volko ff(TOV)equation[59−60]

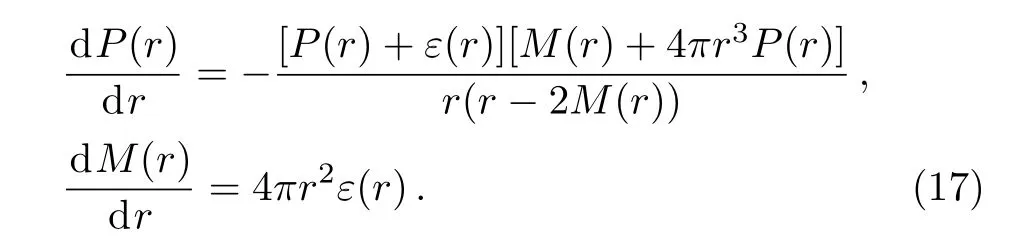
We adopt two successful RMF parameter sets to describe NS matter,GM1 and TM1,as listed in Table 1.[48]These parameters have been determined by fitting to some ground state properties of nuclear matter.As for the couplings of the isoscalar vector mesons ω and ϕ to baryons,we adopt SU(6)spin-flavor symmetry based on the naive quark model and general SU(3)flavor symmetry as listed in Table 2,[49]respectively.

Table 1 The parameter sets GM1 and TM1.The relations,gσ∗N=gρΛ =0,are assumed.We take mω=783 MeV,mρ=770 MeV,mN=938 MeV.For the GM1 and TM1 models,mσ=550 MeV and 511.198 MeV,respectively.[48−49]

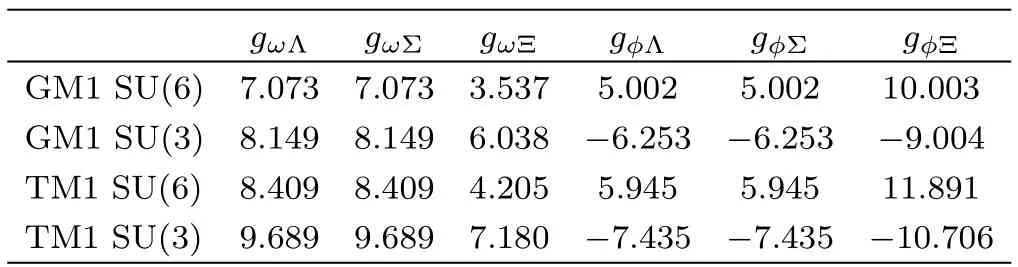
Table 2 The other coupling constants for hyperons.The relations,gρN=(1/2)gρΣ =gρΞ,are assumed.[48−49]

2.2 NS Cooling Theory

The baryon direct Urca processes consist of two successive reactions,beta decay and capture,are listed in Table 3.[35]

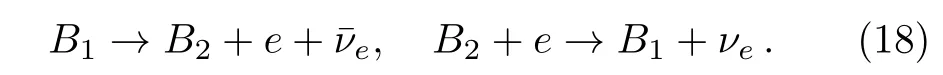
Here B1and B2represent baryons.Due to the EOSs of NSs are derived by RMF model,so the neutrino energy losses must be consistent with the used relativistic EOSs.In the free relativistic gas,the energy and momentum conservations require a large effective mass differece of B1and100 MeV,which is unlikely to appear in the reactions A,D,and G.The reason is that the effective masses of hyperons with the same species but the different isospins are same(see Eq.(9)for details).Therefore,in the relativistic regime,the energy conservation should be assured by considering the potential energy difference of B1and B2.The neutrino emissivity can be given by the Fermi Golden Rule

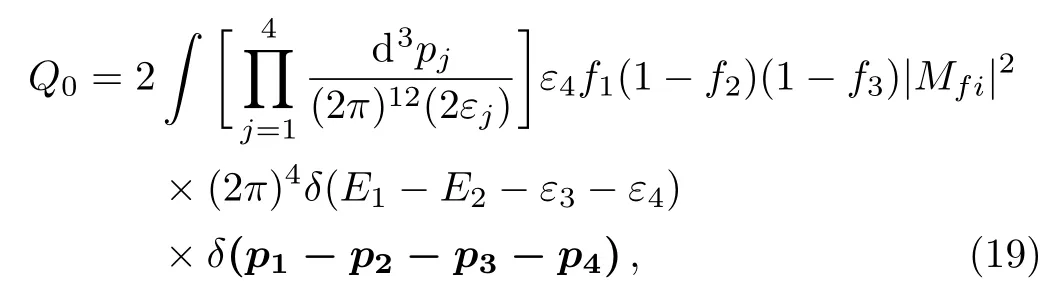
where pj,εjexpress the momentum and kinetic energy of particle species j(j=1,2,3,and 4 refer to B1,B2,e and),respectively.fjis the Fermi-Dirac distribution functions of baryons and electrons,

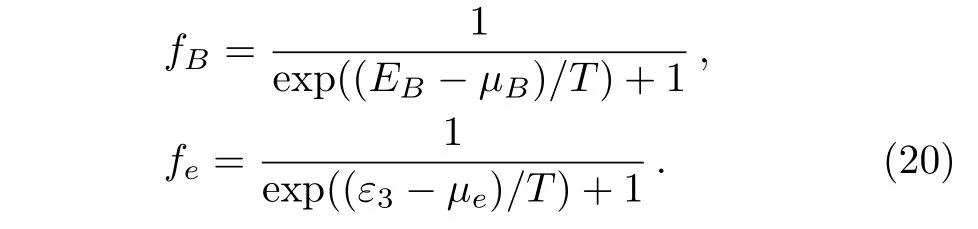
The delta functions δ(E1− E2− ε3− ε4)and δ(p1−p2−p3−p4)describe the energy and momentum conservation,respectively. E1,2=ε1,2+U1,2denote the single-particle energies of baryons,U1,2are the selfconsistent potentials of baryons,which can be obtained in Subsec.2.1 and have the following form

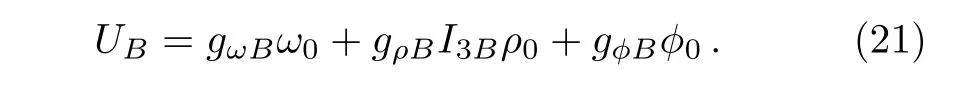
Namely,

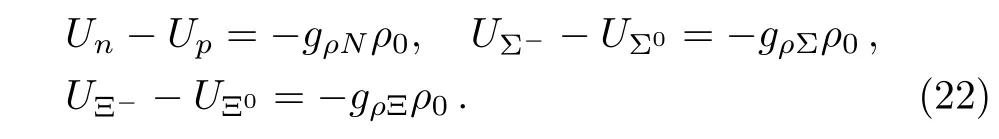
|Mfi|2is the squared matrix element of the baryon direct Urca processes summed over spins of initial and final particles

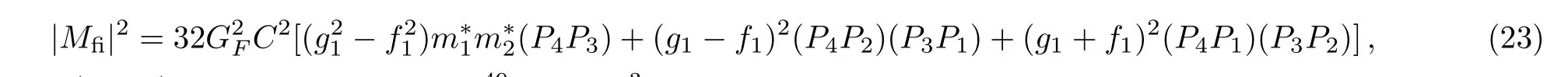
where Pj=(εj,pj).GF=1.436 × 10−49erg·cm3is the weak-coupling constant.f1,g1and C are the vector,axial-vector constants and Cabibbo angle,which are given in Table 3.

Table 3 The constants of the baryon direct Urca processes.We take sinθc=0.231± 0.003,F=0.477±0.012,D=0.756±0.011.

The relativistic expression of the energy loss Q per unit volume and time in NS matter is found to be[61−62]

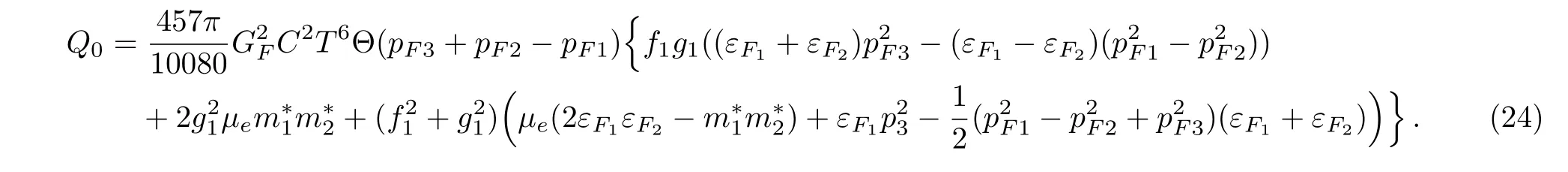
In this expression,pF1,pF2,and pF3are the Fermi momenta of baryons and leptons. εF1and εF2are the kinetic energy of baryon at the Fermi surface.Θ=1 if the Fermi momenta pF1,pF2,pF3satisfy the triangle condition and Θ=0 otherwise.The situation of muons is similar to that of electrons.

The cooling equation based on the approximation of isothermal interior is,

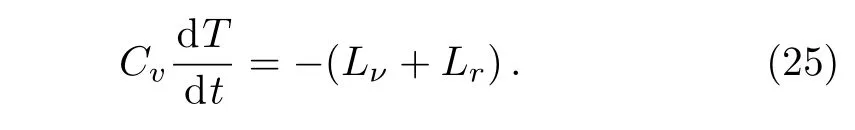
Here Lνand Lrare the total neutrino and photon luminosities,respectively.Cvis the total thermal capacity of NS matter.They are where σ is the Stefan-Boltzmann constant, eΦ=

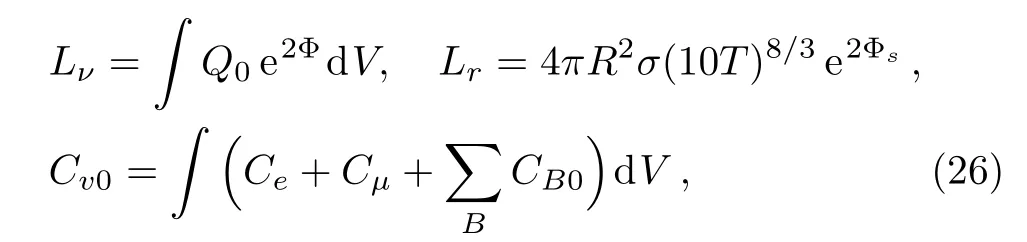
2.3 1S0Superfluidity of Protons

The key quantity in determining the onset of the proton1S0superfluid is the gap function∆(p),

where ε(p)=E(p) − E(pFp).V(p,p′)is the protonproton potential matrix element.In this work,we use the Reid soft core(RSC)potential for the proton-proton potential,[63−66]as an example to demonstrate the influence of hyperons on the proton1S0pairing gaps.The critical temperature Tcpof the proton1S0superfluid is given by the pairing gap∆(p)at zero temperature approximation,

As a result,the neutrino emissivity and thermal capacity can be written as

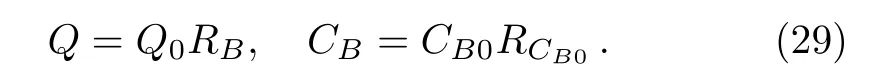
Here RBand RCB0are the superfluid reduction factors of the neutrino emissivity and thermal capacity,respectively.

For the proton1S0superfluid,the reduction factors Rpand RCp0are

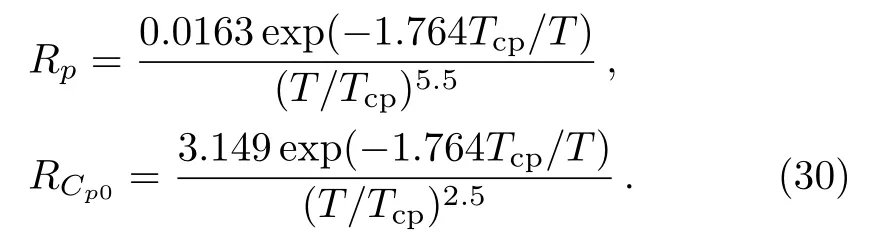
According to the discussion of the RMF approach above,we can obtain the EOS,the mass-radius relations,the neutrino emissivities of the baryon direct Urca processes,the Fermi momenta and the single particle energies of protons,the pairing gap and the critical temperature of the proton1S0superfluid as well as the speed of NS cooling.

3 Results and Discussion

In this section,we give three cases in Eq.(1)for RMF theory:(i)The non-strange σ,ω,ρ mesons are included in SU(6)spin-flavor symmetry;(ii)The σ,ω,ρ mesons including strange mesons σ∗and ϕ are considered in SU(6)spin-flavor symmetry;(iii) σ,ω,ρ,σ∗and ϕ mesons are taken into account in SU(3)flavor symmetry.We mainly study the effects of the degrees of freedom of hyperons and the reactions B,C on the EOS,the neutrino emissivity,the neutrino luminosity,the energy gap of the proton1S0superfluid and NS cooling.Then we compare our results with PSR J1614-2230 and J0348+0432,whose measured masses are used as reference values.

Fig.1 EOSs including hyperons in NS matter.

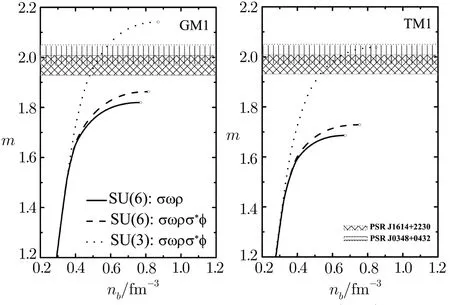
Fig.2 Mass of NS as a function of the total baryon number density nb.

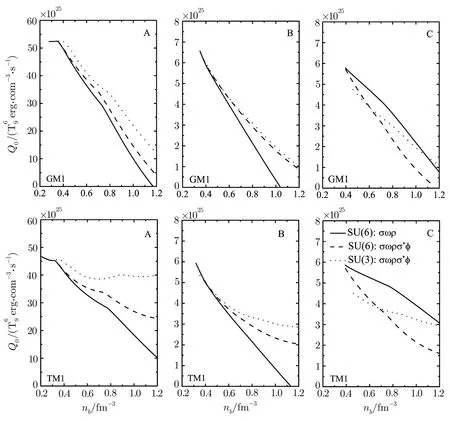
Fig.3 Neutrino emissivities of the reactions A,B and C as a function of the total baryon number density nbin npheµmatter.

Fig.4 Total neutrino emissivities of the reactions AF as a function of the total baryon number density nb.The solid and dotted lines are the neutrino emissivity of the reaction A in npeµ and npheµ matter,respectively.The dashed line is the total neutrino emissivities of the reactions A-F in npheµmatter.

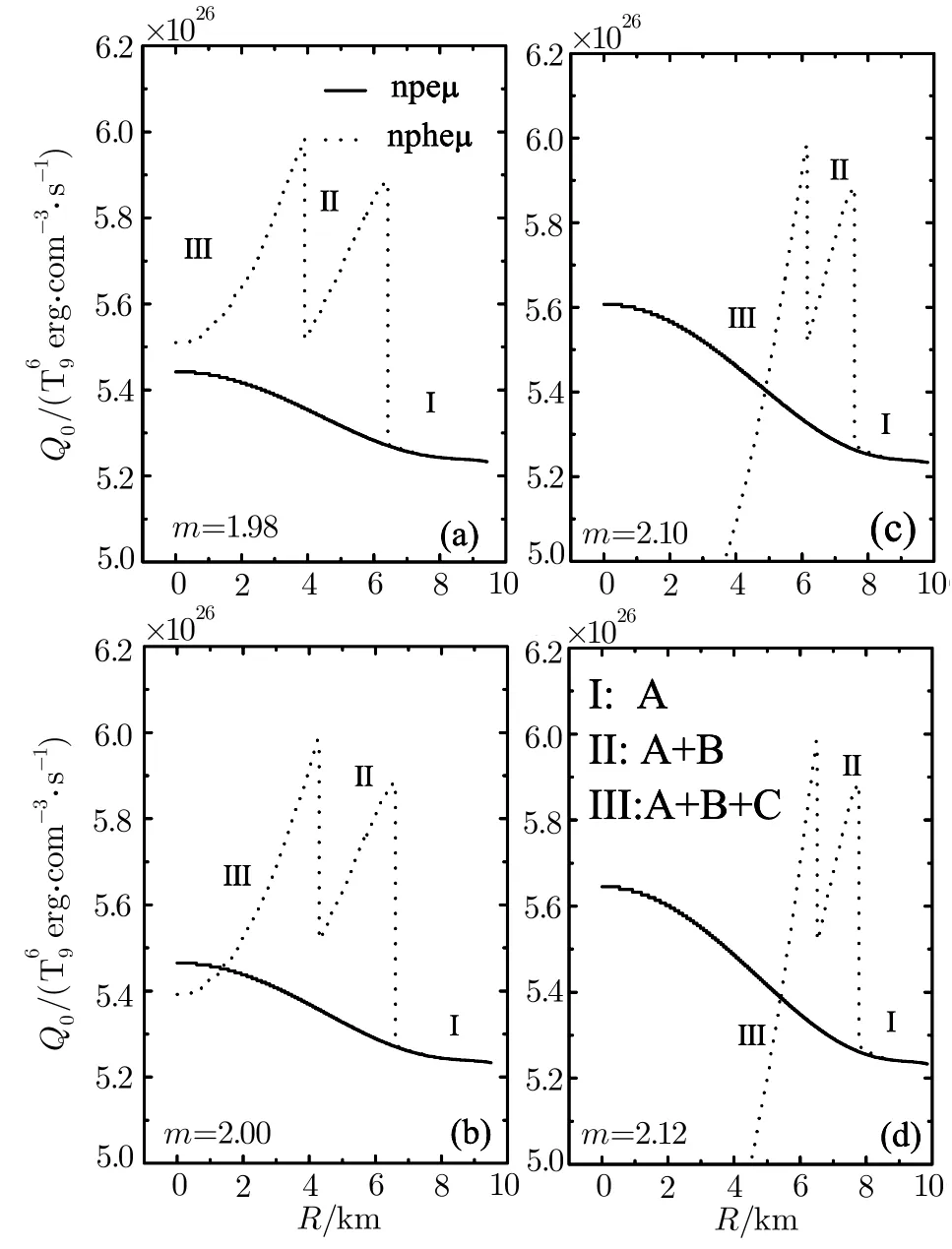
Fig.5 Radial distributions of the total neutrino emissivities with different mass NSs in npeµ(solid lines)and npheµmatter(dotted lines)for the GM1 model.

Figure 1 shows the EOSs in the three cases.Figure 2 shows the mass-radius relations of NSs by solving the TOV equation.The softest and hardest EOSs are obtained by cases(i)and(iii),respectively.Though the coupling gωNfor case(iii)is smaller than the corresponding value for case(i)as shown in Table 1,the total repulsive force is attributed not only to ω meson but also to ϕ meson.As seen in Figs.1 and 2,though we consider the contribution of the strange mesons σ∗and ϕ on the EOS in case(ii),the coupling gϕN=0.It means that ϕ meson only couples to hyperons and makes the EOS be not enough stiff.So the hardest EOS is obtained only through the ϕ meson in case(iii).From case(i)to(iii),the maximum mass of NS(the corresponding center density)sequently increases from 1.820(0.771),1.863(0.817)to 2.141 M⊙(0.871)for the GM1 model,1.686(0.673),1.729(0.754)to 2.038 M⊙(0.848)for the TM1 model,respectively(Fig.2).Namely,the EOS in SU(3)flavor symmetry could be consistent with the observed values of PSR J1614-2230 and J0348+0432 when hyperons appear in NS core.Figure 3 depicts the neutrino emissivities of the reactions A,B and C in npheµmatter for the three cases.As can be seen from Fig.3,the neutrino emissivity of the reaction A has a tendency to decrease with increasing of the total baryon number density nbwhich is due to that the presence of the degrees of freedom of hyperons in NS matter decreases the nucleon and lepton fractions in accordance with the charge neutrality and β equilibium conditions(Eqs.(13)and(14)).The neutrino emissivities of the reactions B and C are obviously less than that of the reaction A because of the smaller matrix elements of the reactions B and C in Eq.(23).The strongest neutrino emissivities of the reactions A and B are obtained in case(iii),while the weakest neutrino emissivities of the reactions A and B are given in case(i).For the reaction C,the neutrino emissivity in case(iii)is less than the corresponding values in cases(i)and(ii) firstly and then increases,equals or exceeds the values in cases(i)and(ii).In order to make the effects of hyperons more intuitive,the total neutrino emissivity of the reactions A-F in npheµmatter comparing with the neutrino emissivity of the reactions A in npeµmatter is depicted in Fig.4.We can see that the neutrino emissivity of the reactions A has been conspicuously suppressed because of the appearance of the degrees of freedom of hyperons.From Figs.2,3,and 4,the mass ranges of the reactions B and C in case(iii)are(1.671–2.141)M⊙and(1.888–2.141)M⊙for the GM1 model,(1.579–2.038)M⊙and(1.849–2.038)M⊙for TM1 model,respectively.Furthermore,the threshold densities of the reactions D-F are larger than the center densities for the maximum masses of NSs,it leads to that the reactions D-F would never happen within stable NSs.Given the above,we only consider the reactions A,B,and C in case(iii)for the following discussion.

Figure 5 gives the radial distributions of the total neutrino emissivities of the reactions A,B,and C for the GM1 model in case(iii),we choose the mass of NS m=(1.98,2.00,2.10,and 2.12)M⊙.The radial distributions of the total neutrino emissivities for a fixed mass NS are nearly invariable when radius r is relatively large(sse Part I for details)with and without the degrees of freedom of hyperons.However,the reactions B and C happen in succession with the reduction of the radius(see Part II and III for details)which leads to that the radial distributions of the total neutrino emissivities with the degrees of freedom of hyperons are significantly larger than the corresponding values without the degrees of freedom of hyperons.Yet with growing mass,the appearance of hyperons obviously shrinks the scope of radius for the growth of the radial distributions of the total neutrino emissivities.The situation of the TM1 model is like the above in GM1 model.Figure 6 shows the total neutrino luminosity as a function of the NS’s mass for the GM1 and TM1 models in case(iii).As seen from Fig.6,whether hyperons are included or not,the neutrino luminosity increases firstly and then decreases with increasing of the NS’s mass.Once the NS’s mass reaches a value,one value of the neutrino luminosity corresponds to two different NSs.And the total neutrino luminosities of reactions A,B and C within the mass range(1.603–2.067)M⊙and(1.515–1.840)M⊙will be larger than the corresponding values in npeµmatter for the GM1 and TM1 models,respectively.Figure 7 shows the critical temperature of the proton1S0superfluid as a function of the total baryon number density nbfor case(iii)including and not including the degrees of freedom of hyperons,respectively.

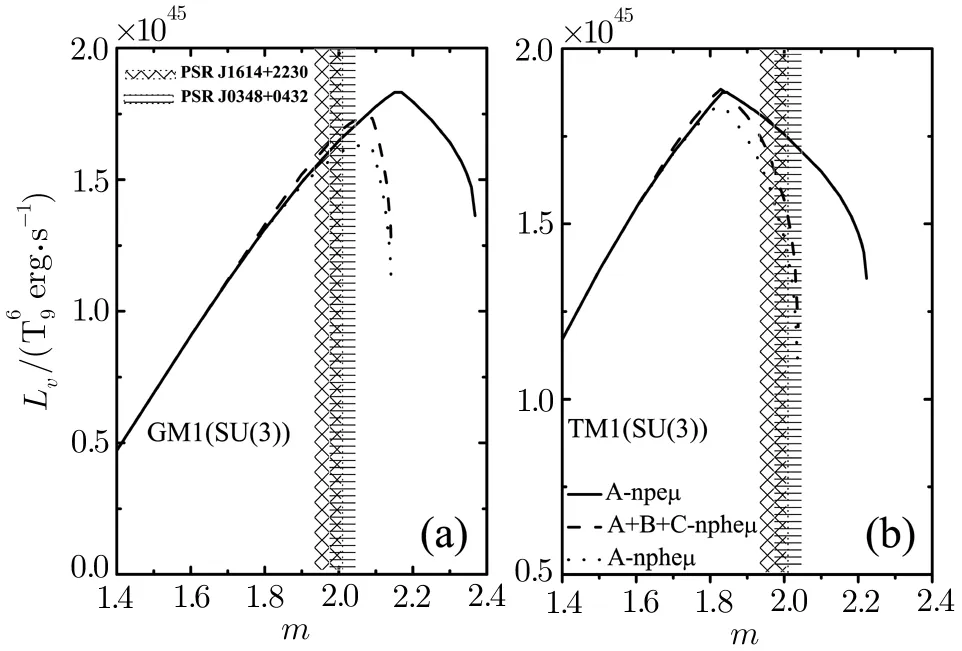
Fig.6 Total neutrino luminosities of the reactions A,B and C as a function of the NS’s mass m.The solid and dotted lines are the neutrino luminosity of the reaction A in npeµ and npheµ matter,respectively.The dashed line is the total neutrino luminositits of the reactions A,B and C in npheµmatter.

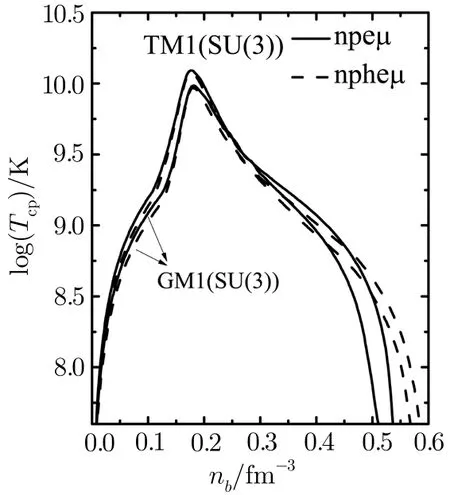
Fig.7 The critical temperature Tcpof the proton1S0 superfluid as a function of the NS’s mass m in npeµ matter(solid lines)and npheµmatter(dashed lines),respectively.

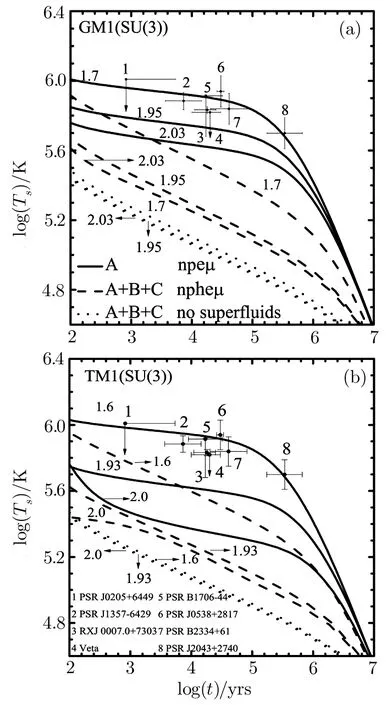
Fig.8 Observational data(error bars)on surface temperatures of 8 NSs as compared with theoretical cooling curves obtained by the proton1S0superfluid for the GM1 and TM1 models,respectively.The solid lines correspond to npeµmatter,the dashed lines correspond to npheµmatter with masses(from top to bottom)(1.7,1.95 and 2.03)M⊙for the GM1 model((1.6,1.93 and 2.0)M⊙for the TM1 model),respectively.The dotted lines represent cooling curves in the non-superfluid NS matter.

In Fig.7,one can see that whether or not the NS core appears hyperons,the critical temperature of the proton1S0superfluid increases first,but it gradually decreases after it reaches maximum along with increasing of the total baryon number density nb.While when hyperons appear in NS core,the critical temperature of the proton1S0superfluid is first below and then above the corresponding values in npeµmatter within the density ranges of nb=(0.0–0.454)fm−3(nb=(0.0–0.418)fm−3for the TM1 model)and nb≥ 0.454 fm−3(nb≥ 0.418 fm−3for the TM1 model)for the GM1 model,respectively.This is because the total contributions of the Fermi momentum,the effective mass and the single-particle e nergy of protons result in the change of the critical temperature of the proton1S0superfluid.Furthermore,the appearance of hyperons widens the scope of the baryon number density for the proton1S0superfluid in NS matter,which can further inhibit the baryon direct Urca processes as well as affect the cooling of NSs.The theoretical cooling curves with the proton1S0superfluid assuming the isothermal stars are obtained in Fig.8 for the GM1 and TM1 models,respectively.Observational data of 8 isolated NSs whose effective surface temperatures have been measured or constrained is listed as compared with the theoretical cooling curves.[67−75]As you can see from Fig.8,the cooling curve of an NS with the moderate mass can be a great way to explain the observational data,while the cooling curves of massive NSs are difficult to explain the existing observational data due to the low surface temperature.The continued decline in the cooling curves along with the growth of the NS’s mass means that a massive NS will go through the fast cooling process whether the degrees of freedom of hyperons appear.In addition,from Fig.6 we can see that the neutrino luminosities of(1.70,1.95,2.03)M⊙NSs for the GM1 model((1.60,1.93,2.00)M⊙NSs for the TM1 model)in npheµmatter are greater than the corresponding values in npeµmatter,respectively.While from Fig.7,we can also see that the critical temperatures Tcpof(1.70,1.95,2.03)M⊙NS for the GM1 model((1.60,1.93,2.00)M⊙NSs for the TM1 model)in npheµmatter are lower than the corresponding values in npeµmatter.It results in the fact that the suppression of the neutrino emissivities for the reactions A and B is delayed in npheµmatter,so the cooling speeds of(1.70,1.95,2.03)M⊙NS for the GM1 model((1.60,1.93,2.00)M⊙NSs for the TM1 model)with the degrees of freedom of hyperons(dashed lines)are quicker than the corresponding values without the degrees of freedom of hyperons(solid lines).The proton1S0superfluid does not affect the reaction C in(1.70,1.95,2.03)M⊙NS for the GM1 model((1.60,1.93,2.00)M⊙NSs for the TM1 model),which is due to that the threshold density of the reaction C in the above NSs is higher than the baryon number density of the appearance of the proton1S0superfluid in the above NSs.Therefore,although the neutrino emissivities of the reactions A and B are suppressed with the presence of the proton1S0superfluid,the total contributions of reactions A,B and C can still speed up a massive NS cooling.Our model may be a simplification because it adopts the lowest level of approximation in the gap equation as well as neglecting the possible influence of inhomogeneity in NS crust and hyperon superfluidity in NS core on the reactions A,B and C,however,it can still clearly describe the effects of the proton1S0superfluid on the reactions A,B and C in NS matter.We will analyze more complicated models in future studies.

4 Conclusion

We have studied the effects of the degrees of freedom of hyperons,the reactions B and C on the reaction A in NS matter using the two popular RMF parameter sets,GM1 and TM1,respectively.Firstly,we used the SU(3)flavor symmetry to obtain the stiffEOS which led to the degrees of freedom of hyperons appearing in PSR J1614-2230 and J0348+0432.Secondly,the total neutrino luminosities of the reactions A,B and C were calculated in npeµand npheµmatter,respectively.We found that the presence of the reactions B and C made the total neutrino luminosities higher than the corresponding values without the reactions B and C within the mass range(1.603–2.067)M⊙for the GM1 model and(1.515–1.840)M⊙for the TM1 model,respectively.The cooling rate with hyperons was faster than the corresponding value without hyperons for a fixed NS.It illustrated that though the appearance of hyperons has obviously suppressed the neutrino emissivity of the reaction A,which had the highest neutrino emissivity in npeµmatter,the contribution of the reactions B and C could still lead to the rapid cooling for the massive NSs.In particular,because the threshold densities of the reaction C in PSR J1614-2230 and J0348+0432 were significantly higher than the baryon number density for the proton1S0superfluid,thus the reaction C was not suppressed by the proton1S0superfluid which will further speed up the two pulsars cooling.These features maybe can help to prove the presence of hyperons in the cores of PSR J1614-2230 and J0348+0432.

[1]D.G.Yakovlev and C.J.Pethick,Ann.Rev.Astron.Astrophys.42(2004)169.

[2]D.G.Yakovlev,et al.,AIP Conf.Series.983(2008)379.

[3]J.J.Liu,Q.H.Peng,and D.M.Liu,Chin.Phys.C 41(2017)095101.

[4]C.R.Ji and D.P.Min,Phys.Rev.D 57(1998)5963.

[5]D.G.Yakovlev,K.P.Leven fish,and Y.A.Shibanov,Phys.Uspek.42(1999)737.

[6]E.G.Zhao and F.Wang,Chin.Sci.Bull.56(2011)3797.

[7]Z.F.Gao,et al.,Astrophys.Space Sci.334(2011)281.

[8]H.Sotani,T.Maruyama,and T.Tatsumi,Nucl.Phys.A 906(2013)37.

[9]C.Schaab,S.Balberg,and J.Schaffner-Bielich,Astrophys.J.504(1998)L99.

[10]Y.N.Wang and H.Shen,Phys.Rev.C 81(2010)025801.

[11]Y.Xu,et al.,Research in Astron.Astrophys.15(2015)725.

[12]C.J.Xia,G.X.Peng,E.G.Zhao,and S.G.Zhou,Phys.Rev.D 93(2016)085025.

[13]Z.F.Gao,H.Shan,W.Wang,and N.Wang,Astron.Nachr.338(2017)1066.

[14]Y.Xu,et al.,Mon.Not.R.Astron.Soc.474(2018)3576.

[15]C.J.Xia and S.G.Zhou,Nucl.Phys.B 916(2017)669.

[16]C.Zhu,Z.F.Gao,X.D.Li,et al.,Mod.Phys.Lett.A 31(2016)1650070.

[17]S.Tsuruta,Phd.Thesis,Columbia University(1964).

[18]E.Flowers,M.Ruderman,and P.Sutherland,Astrophys.J.205(1976)541.

[19]O.V.Maxwell,Astrophys.J.231(1979)201.

[20]E.H.Gudmundsson,C.J.Pethick,and R.I.Epstein,Astrophys.J.272(1983)286.

[21]D.Page and J.H.Applegate,Astrophys.J.394(1992)17.

[22]A.D.Kaminker,P.Haensel,and D.G.Yakovlev,Astron.Astrophys.373(2001)L17.

[23]D.G.Yakovlev,et al.,Nucl.Phys.A 752(2005)90.

[24]C.Kouvaris,Phys.Rev.D 77(2008)023006.

[25]D.Blaschke,H.Grigorian,D.N.Voskresensky,and F.Weber,Phys.Rev.C 85(2012)022802.

[26]X.L.Mu,H.Y.Jia,X.Zhou,and H.Wang,Astrophys.J.846(2017)140.

[27]J.M.Lattimer,C.J.Pethick,M.Prakash,and P.Haensel,Phys.Rev.Lett.66(1991)2701.

[28]P.Haensel and O.Y.Gnedin,Astron.Astrophys.290(1994)458.

[29]M.E.Gusakov,Astron.Astrophys.389(2002)702.

[30]Y.Xu,et al.,Chin.Phys.Lett.28(2011)079701.

[31]Y.Xu,et al.,Commun.Theor.Phys.56(2011)521.

[32]X.Zhou,M.Kang,and N.Wang,Chin.Phys.C 37(2013)085101.

[33]Y.Xu,et al.,Chin.Sci.Bull.59(2014)273.

[34]X.Zhou,H.Jia,B.Hong,et al.,Int.J.Mod.Phys.D 26(2017)1750077.

[35]M.Prakash,et al.,Astrophys.J.390(1992)77.

[36]J.M.Lattimer,K.A.van Riper,M.Prakash,and M.Prakash,Astrophys.J.425(1994)802.

[37]J.Boguta and A.R.Bodmer,Nucl.Phys.A 292(1977)413.

[38]J.Boguta,Phys.Lett.B 106(1981)250.

[39]J.Boguta and H.Stocker,Phys.Lett.B 120(1983)289.

[40]W.Pannert,P.Ring,and J.Boguta,Phys.Rev.Lett.59(1987)2420.

[41]J.Schaffner and I.N.Mishustin,Phys.Rev.C 53(1996)1416.

[42]F.Yang and H.Shen,Phys.Rev.C 77(2008)025801.

[43]Y.Xu,et al.,Chin.Phys.Lett.30(2013)129501.

[44]Z.F.Gao,N.Wang,H.Shan,et al.,Astrophys.J.849(2017)19.

[45]P.B.Demorest,et al.,Nature(London)467(2010)1081.

[46]J.Antoniadis,et al.,Science 340(2013)448.

[47]S.Weissenborn,D.Chatterjee,and J.Schaffner-Bielich,Phys.Rev.C 85(2012)065802.

[48]T.Miyatsu,M.K.Cheoun,and K.Saito,Phys.Rev.C 88(2013)015802.

[49]S.Weissenborn,D.Chatterjee,and J.Schaffner-Bielich,Nucl.Phys.A 914(2013)421.

[50]L.L.Lopes and D.P.Menezes,Phys.Rev.C 89(2014)025805.

[51]T.Takatsuka and R.Tamagaki,Nucl.Phys.A 738(2004)387.

[52]J.J.Liu and D.M.Liu,arXiv:nucl-th/1711.01955.

[53]J.J.Liu,Q.H.Peng,L.H.Hao,et al.,Research in Astron.Astrophys.17(2017)107.

[54]Z.F.Gao,D.L.Song,Y.L.Liu,et al.,Accepted for Astron.Nachr.338(2017)1060.

[55]Z.F.Gao,X.D.Li,N.Wang,et al.,Mon.Not.R.Astron.Soc.456(2016)55.

[56]G.J.Mao,A.Iwamoto,and Z.X.Li,Chin.J.Astron.Astrophys.3(2003)359.

[57]J.J.Liu and D.M.Liu,Chin.Phys.C 41(2017)125102.

[58]Y.Xu,et al.,Chin.Phys.Lett.29(2012)059701.

[59]J.R.Oppenheimer and G.M.Volko ff,Phys.Rev.55(1939)374.

[60]R.C.Tolman,Phys.Rev.55(1939)364.

[61]L.B.Leinson and A.P´erez,Phys.Lett.B 518(2001)15.

[62]L.B.Leinson,Nucl.Phys.A 707(2002)543.

[63]D.W.L.Sprung and P.K.Banerjee,Nucl.Phys.A 168(1971)273.

[64]L.Amundsen and E.O/stgaard,Nucl.Phys.A 437(1985)487.

[65]S.Nishizaki,T.Takatsuka,N.Yahagi,and J.Hiura,Prog.Theor.Phys.86(1991)853.

[66]J.Wambach,T.L.Ainsworth,and D.Pines,Nucl.Phys.A 555(1993)128.

[67]P.Slane,et al.,Astrophys.J.616(2004)403.

[68]V.E.Zavlin,Astrophys.J.665(2007)L143.

[69]J.P.Halpern,et al.,Astrophys.J.612(2004)398.

[70]G.G.Pavlov,et al.,Astrophys.J.552(2001)129.

[71]K.E.McGowan,et al.,Astrophys.J.600(2004)343.

[72]V.E.Zavlin and G.G.Pavlov,Mem.Soc.Astron.Ital.75(2004)458.

[73]A.Possenti,S.Mereghetti,and M.Colpi,Astron.Astrophys.313(1996)565.

[74]O.Y.Kargaltsev,et al.,Astrophys.J.625(2005)307.

[75]W.C.G.Ho,et al.,Astrophys.J.375(2007)821.