分位数回归方法简介及其在医学研究领域中的应用
潘璐璐 余勇夫 秦国友
(复旦大学公共卫生学院生物统计学教研室 上海 200032)
在公共卫生和医学领域的研究中,经常需要探索暴露因素和某一连续型结局变量之间的关联。以探索睡眠时间与抑郁水平的关联为例,通过均值回归分析可以揭示睡眠时间对研究人群抑郁水平均值的影响。然而,由于抑郁程度较高的群体相较于抑郁程度较低的群体具有更低的血清素水平和更高的炎症水平,睡眠时间的改变对这两个群体的抑郁水平会产生不同影响[1-2]。因此,均值回归的结果可能掩盖了睡眠时间对不同抑郁程度群体的抑郁水平的真实影响,我们需要考虑不同抑郁程度下,睡眠时间和抑郁水平关联是否存在异质性。分位数回归方法可以很好地解决这一问题,该方法可以捕捉自变量对因变量分布不同分位数的影响。例如:当考虑抑郁水平分布0.5 的分位数(中位数)时,分位数回归能够揭示睡眠时间对处于抑郁水平中间位置的研究人群抑郁水平的影响;当分位数为0.9 时,分位数回归能够揭示睡眠时间对抑郁程度高(抑郁水平处于研究人群前10%)的群体抑郁水平的影响。分位数回归能够探索在因变量不同分位数水平下自变量与因变量的关联性,从而全面揭示两者之间的关系。
目前,分位数回归方法已得到了广泛的应用。在精神疾病研究领域中,一项大样本量的横断面研究[3]揭示了精神障碍状态与残疾水平的关联在高残疾人群中更强,反映了对此群体进行精神健康护理的重要性。在营养流行病学研究领域中,有学者[4]通过分位数回归方法发现,不溶性膳食纤维摄入量和升糖指数与糖化血红蛋白水平的关联在血糖控制状况较差的中国糖尿病患者中更强,为糖尿病患者在营养管理方面提供了重要线索。此外,分位数回归方法也是环境流行病学研究领域常用的一个有价值的工具。一项利用该方法的研究[5]发现,空气污染对心血管疾病相关的DNA 甲基化程度较低的老年男性的影响更强;另一项研究[6]发现,儿童早期的空气污染暴露与青春期动脉粥样硬化标志物低水平相关,提示了降低生活早期交通相关空气污染对于延缓动脉粥样硬化及心血管疾病发展的重要性。因此,分位数回归方法能全面地描述因变量不同分位数下自变量和因变量的关联,识别高危人群或者干预的最佳受益人群,为干预措施的制定提供线索。
分位数回归方法原理假定y是感兴趣的连续型因变量,X=(X1,X2,…,Xp)是p维自变量,分位数回归模型可以表示为:
其中i指第i个样本,Qτ(yi|Xi)是给定自变量Xi下yi的第τ个条件分位数,不同于普通最小二乘回归模型中给定自变量Xi下yi的条件均值E(yi|Xi)。表示给定其他自变量值后,Xj每改变一个单位,Qτ(yi|Xi)的改变程度。参数βτ可以通过下面的公式进行估计:
其中,ρτ(u)是分位数回归的损失函数,I(·)是指示函数。当yi-Xi βτ≥0 时,ρτ(yi-Xi βτ)=(yi-Xi βτ)τ;当yi-Xi βτ<0 时,ρτ(yi-Xi βτ)=(yi-Xi βτ)(τ-1)。可以使用梯度下降等优化方法最小化这个损失函数来获得参数的估计[7]。在R 语言中,quantreg包的rq()函数提供了实现分位数回归的工具,函数内部使用了相应的优化算法来拟合分位数回归方法[8]。
实例分析我们通过以下实例分析来介绍分位数回归方法的应用,以探索睡眠时间和抑郁水平的关联。数据来源于2015 年1 月—2020 年3 月美国一项全国健康和营养调查(National Health and Nutrition Examination Survey,NHANES)收集的研究数据(https://www.cdc.gov/nchs/nhanes/index.htm)。这是一项基于人群的横断面调查,旨在收集美国成人和儿童的健康和营养状况信息。NHANES 采用患者健康问卷(Patient Health Questionnaire-9,PHQ-9)来评估调查对象的抑郁程度,问卷一共包括9 个询问过去2 周内抑郁症状出现频率的问题,回答分为“完全没有”、“几天”、“半天以上”和“几乎每天”4 个类别,分值为0~3,总分为0~27。自我报道的睡眠时间定义为工作日晚上平均睡眠时间,对照组正常睡眠定义为6~9 h,短睡眠和长睡眠时间分别定义为少于6 h 和超过9 h。协变量调整了年龄、性别、种族、教育程度、家庭收入、婚姻状况、体育活动、吸烟状况和饮酒状况。本研究随机选取了5 000 名年龄范围在18~80 岁的研究对象,排除睡眠时间、抑郁程度得分和重要协变量有缺失数据的研究对象,使用完整数据集进行分析。
图1 展示了抑郁水平不同分位数下回归系数的折线图,图中的阴影部分表示分位数回归系数估计值的95%置信区间(95%CI),水平实线是普通最小二乘回归的系数估计值,虚线为95%置信区间。均值回归结果表明,短睡眠和长睡眠时间相比于正常睡眠时间,平均抑郁水平显著增加了1.80(95%CI:1.43,2.17)和1.34(95%CI:0.78,1.91)。而分位数回归结果显示,随着分位数的增加,睡眠时间和抑郁水平的关联强度也增加,在较高分位数(例如0.8 或0.9),短睡眠和长睡眠时间与抑郁水平的关联强度均强于均值回归估计的关联强度(表1)。例如,短睡眠时间和长睡眠时间相比正常睡眠时间,0.9 分位数的抑郁水平分别增加了3.99(95%CI:2.57,5.42)和2.73(95%CI:1.13,4.32)。因此,睡眠时间对抑郁水平的影响程度在抑郁水平不同分位数下是异质的(异质性检验的P均<0.001)。
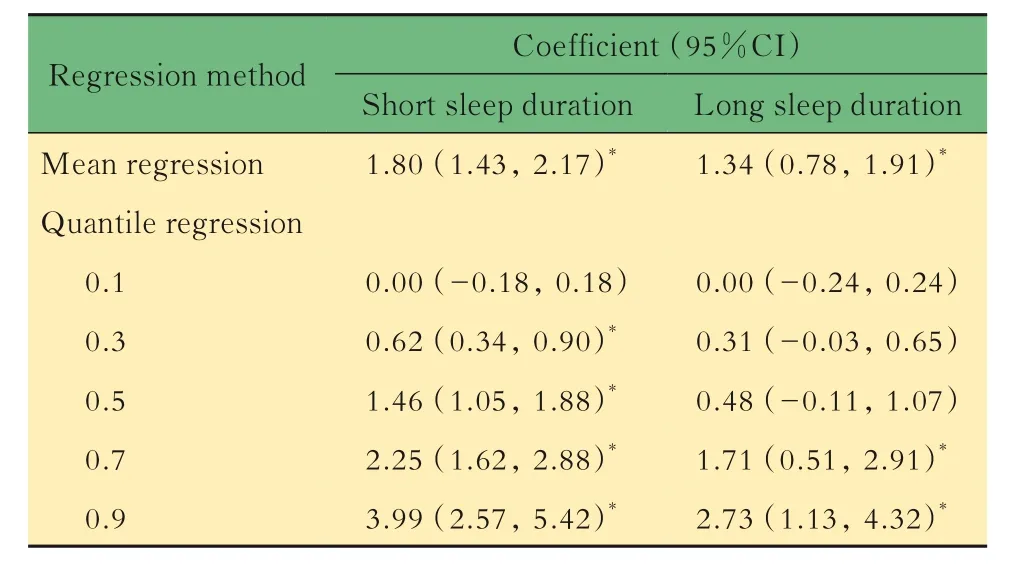
表1 均值回归模型和分位数回归模型的系数估计值Tab 1 Coefficients of mean regression model and quantile regression model
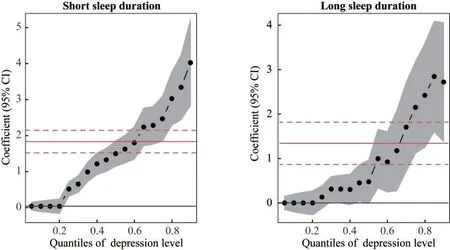
图1 分位数回归系数折线图Fig 1 Line chart of quantile regression coefficients
总结在公共卫生和医学研究中,我们习惯报道暴露因素对结局均值的影响。然而,这可能掩盖在结局分布不同分位数水平下可能存在的关联的异质性,我们可以通过分位数回归方法全面展现暴露和结局在结局分布不同分位数上的关联。正如我们的案例所示,仅报道均值回归的结果,会高估睡眠时间对低抑郁程度群体的抑郁水平的影响,同时低估睡眠时间对高抑郁程度群体的抑郁水平的影响。而分位数回归能够呈现自变量在任意分位数下与因变量的关联,揭示了均值回归无法发现的结果:(1)在低抑郁程度的群体中,相比正常睡眠时间,睡眠时间不足或过长与抑郁水平没有显著关联;(2)抑郁程度越高的群体,其抑郁水平受睡眠时间不足或过长的影响更大。因此,采用该方法得到的研究结果为将来的干预方案提供了有参考价值的信息:严重的抑郁症患者在治疗中可能需要个性化的睡眠管理,即使在抑郁症状减轻后也需要加强睡眠护理[9]。此外,分位数回归对异常值更稳健,无需同方差假设[10]。
因此,分位数回归方法是一种适用于分析连续型因变量和感兴趣自变量之间全面关联的有力工具,其应用不需要额外的数据,却能够提供更为丰富的研究结果[11]。目前在R、Stata 和SAS 中都有完善的软件包可用于实现分位数回归。在中大型医疗健康数据的研究中,使用分位数回归可以提供全面的线索,为后续深入研究提供有力支持,还可以识别出对暴露因素更敏感的亚组人群,为制定针对该人群的临床和公共卫生干预措施提供建议。我们建议,研究人员在今后的研究中可以尝试运用分位数回归方法,以揭示自变量和因变量之间的全面关联。
作者贡献声明潘璐璐 数据整理,结果分析和解释,论文撰写。余勇夫 课题构思与设计,论文修订。秦国友 课题构思与设计,获取资助,监督指导,论文修订。
利益冲突声明所有作者均声明不存在利益冲突。
——与非适应性回归分析的比较

