基于改进瞪羚优化算法的机器人路径规划

邓 毅,廖秋丽

(1.桂林师范高等专科学校物理与工程技术系,广西 桂林 541199)(2.桂林电子科技大学电子工程与自动化学院,广西 桂林 541004)

移动机器人是涵盖了环境数据采集、动作执行、规划作业等多性能的综合性移动硬件平台[1-5],其可以实现自主行驶、定位导航、环境感知及人机交互等各类行为。移动机器人已经广泛应用于车站、机场和邮局等场所,并迅速在日常生活中占据重要地位。机器人在复杂或不确定的实际环境中导航时,必须规划出合适的移动路径。路径规划即在指定的环境中寻得一条无碰撞的路径,其在过去的几十年里得到了快速发展。

近年来,研究人员提出了各种不同的路径规划方法并在机器人或自动导引车(automated guided vehicle,AGV)上加以应用。经典的路径规划算法包括遗传算法(genetic algorithm,GA)[6]、蚁群优化算法(ant colony optimization,ACO)[7]、快速探索随机树算法(rapidly-exploring radom tree,RRT)[8]、A*算法[9]、人工势场法[10]、强化学习[11]等。当前移动机器人工作环境愈发复杂,许多经典算法已无法满足机器人规划需求。因此,需要寻得一种高效、安全的路径规划算法,帮助机器人完成规划作业。

瞪羚优化算法(gazelle optimization algorithm,GOA)是一种新颖、简单、搜索能力强的全局随机优化算法,于2022年被提出。研究表明,GOA相比其他先进的启发式算法在优化问题上有更好表现[12]。因此,本文尝试将GOA应用于机器人路径规划领域,提出一种改进的瞪羚优化算法(improved gazelle optimization algorithm,IGOA)。对其存在的易早收敛、规划效率低等问题,利用正交学习及Rosenbrock直接旋转两种策略进行改进,从而提升算法综合性能,帮助机器人高效完成规划任务。

1 瞪羚优化算法

对于猎豹和狮子等掠食者来说,瞪羚的奔跑速度非常快。大多数掠食者能否成功取决于它们是否能隐蔽地跟踪瞪羚;如果不能出其不意,瞪羚大多会以高速跑过捕食者。GOA就是以瞪羚逃避捕食者的行为为核心思想来进行探索和开发,具体模型如下:

1)初始化。

GOA是一种基于种群的优化算法,它使用随机初始化的瞪羚作为搜索个体。搜索个体为候选解的n×d矩阵,表达式如下:

(1)

式中:X为候选种群的位置向量矩阵;xi,j为第i个种群在第j维随机生成的向量位置,i=1,2,…,n,j=1,2,…,d,其中n为瞪羚数量,d为维数。xi,j表达式如下:

xi,j=rand×(UBj-LBj)+LBj

(2)

式中:rand为随机数,UBj和LBj分别为种群的上界和下界。在每次迭代中,每个个体xi,j产生一个候选解。将目前得到的最优解命名为顶端瞪羚,构造一个精英矩阵E。该矩阵用于为瞪羚进行下一步搜索,其表达式如下:

(3)

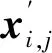
2)开发阶段。

这个阶段假设瞪羚在没有捕食者或者当捕食者跟踪瞪羚时只是安静地吃草。在这一阶段,利用布朗运动进行开发。假设瞪羚在吃草时以布朗运动进行活动,具体模型表示如下:

gi+1=gi+s·R·RB·(Ei-RB·gi)

(4)

式中:gi+1为下一次迭代的解,gi为当前迭代的解,s为瞪羚的掠食速度,RB为布朗运动的随机数向量,R为[0,1]内的均匀随机数向量,Ei为精英矩阵。

3)探索阶段。

一旦瞪羚个体发现捕食者,探索阶段就开始了。此阶段采用了Levy飞行,整个过程包括小步前进和偶尔的跳跃。假设每次迭代都发生方向突变;当迭代次数为奇数时,瞪羚向一个方向移动,当迭代次数为偶数时,瞪羚向另一个方向移动。瞪羚首先做出反应,捕食者的反应较慢,所以假设它的跑动过程是按照布朗运动进行,然后再换成Levy飞行。当瞪羚发现捕食者后,其行为的数学模型如下:

gi+1=gi+S·μ·R·RL·(Ei-RL·gi)

(5)

式中:μ为常数,S为瞪羚能达到的最高速度,RL为基于Levy分布的随机数向量。捕食者追逐瞪羚的行为的数学模型如下:

(6)

式中:iter为当前迭代次数,max_iter为最大迭代次数。

设PSRs代表捕食者成功率,可利用PSRs防止GOA陷入局部最小值。位置更新具体模型如下:

(7)

(8)

式中:UB和LB分别为种群的上界和下界,U为二进制向量,r为[0,1]中的随机数,gr1和gr2为瞪羚矩阵的随机指数。

2 改进瞪羚优化算法

2.1 正交学习机制

分数实验是正交设计的核心。利用部分实验的特征产生所有可能的水平组合,可以快速找到最佳水平组合。为每个变量寻找最佳水平组合的标准方法是遍历所有水平组合,假设客观问题依赖于K个因子,且可以被分成Q个水平。这种遍历方法不同于正交设计,其构建过程如下:首先构建介绍性列,然后构建非基本列。式(9)为创建的L10(34)的正交数组。

(9)

2.2 Rosenbrock直接旋转策略

在Rosenbrock直接旋转局部搜索策略中,坐标轴主要用于初始路径的搜索,种群个体沿着坐标轴方向旋转,然后移动到新的排列点,同时在此处产生有效解,直到在每个搜索方向至少产生一个有效解和一个无效解。在这种情况下,当前阶段将结束搜索,标准正交基将被修改,并且考虑所有维度中全部有效解的累积影响。标准正交基更新如下:

(10)

式中:xk+1为第k个个体的下一代有效解,xk为本次迭代有效解,di为第i个个体的坐标,λi为设计变量的总数。此时最有利的搜索方向是xk+1-xk,因此它必须包含在修正的搜索方向中。

(11)

式中:pi为标准正交向量,dj为第j个个体的坐标。Gram-Schmidt正交归一化过程更新搜索结果如下所示:

(12)

式中:qj为标准正交向量。

归一化时修改的搜索指令为:

(13)

在更新局部搜索之后,在相反方向再次搜索,直到满足结束条件。

2.3 算法流程

本文算法具体流程如图1所示。

图1 算法流程

3 仿真及分析

3.1 仿真实验

为验证本文算法性能,采用本文算法与标准GOA、文献[8]和文献[10]算法基于MATLAB R2020b平台分别在简易环境及多陷阱环境下进行仿真实验。使用的硬件包括Windows 11操作系统、英特尔酷睿i7-7700@3.60 GHz处理器和16 GB运行内存。本文算法群体大小设置为50,最大迭代次数为100。每个算法的独立运行次数设置为30次。具体结果如图2、图3及表1所示。

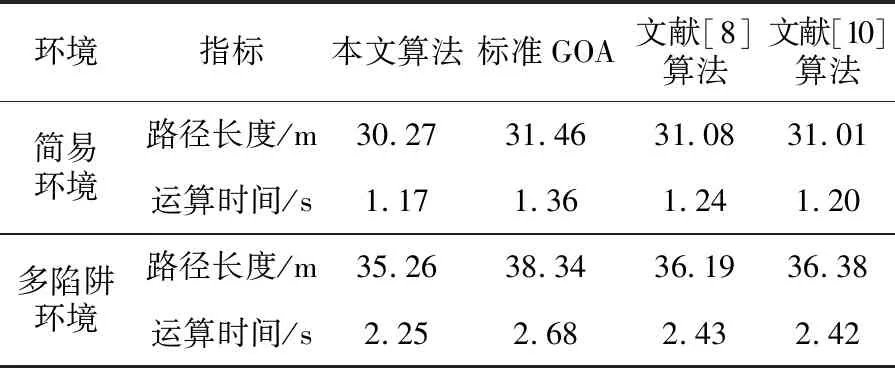
表1 指标对比

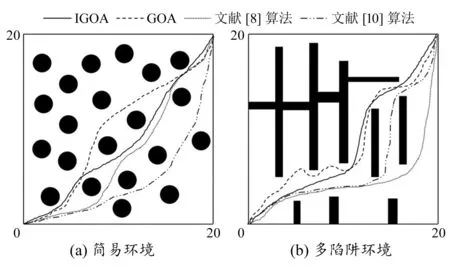
图2 简易环境仿真结果

根据图2及图3可知,4种算法均可以在两种环境中找到无碰路径。从表1的具体指标可以看出,在简易环境中,本文算法相较于标准GOA、文献[8]和文献[10]算法路径长度分别缩短3.79%、2.62%、2.39%,运算时间分别缩短13.97%、5.65%、2.50%。在多陷阱环境中,本文算法相较于标准GOA、文献[8]和文献[10]算法路径长度分别缩短8.03%、2.57%、3.08%,运算时间分别缩短16.04%、7.41%、7.03%。由此可以看出IGOA在路径规划问题上具有优良性能,引入的多种改进策略提升了规划效率,可帮助机器人更快地完成规划任务。

3.2 实车实验

为了验证本文算法在真实场景中的有效性,在实际场景下进行实车实验。实验使用的硬件平台是FS-AIROBOTB智能机器人。将本文算法写入操作系统,利用即时定位与地图构建(simultaneous localization and mapping, SLAM)算法构建测试地图。路径规划实际测试环境和运行结果如图4所示,其中S为起点,G为目标点。

图4 实车实验结果

实验中,建立了IGOA的应用环境,并进行了自主导航测试。实验结果表明,移动机器人能够自主规划出可靠平滑的路径,完成从起点到终点的路径自主导航。该实验验证了IGOA可以应用于移动机器人,并具有应用于工业场景的潜力,展现出良好的适用性及有效性。

4 结束语

针对机器人路径规划中效率低、寻优速度慢等问题,本文设计了一种IGOA。仿真结果表明,在简易环境中,本文算法相较于对比的算法路径长度缩短2.39%～3.79%,运算时间缩短2.50%～13.97%。在多陷阱环境中,本文算法相较于对比算法路径长度缩短2.57%～8.03%,运算时间缩短7.41%～16.04%。同时通过实车实验验证了本文算法的有效性。