考虑剪力滞和剪切变形效应的UHPC箱梁长期挠度分析

马俊军，蔺鹏臻，刘应龙，何志刚

(1.兰州交通大学 土木工程学院，甘肃 兰州 730070；2.兰州交通大学 建筑与城市规划学院，甘肃 兰州 730070)

箱梁因具有抗弯扭刚度大、结构自重轻和造型优美等优点,已在国内外桥梁建设中得到广泛应用[1-2]。大量工程实践和理论研究表明,在长期荷载作用下,由于收缩徐变效应引起的箱梁跨中挠度下挠过大和梁体开裂是导致混凝土箱梁受力性能和耐久性能不断降低的主要原因[3-4]。因此,准确计算和预测箱梁在长期荷载作用下梁体挠度发展规律对我国混凝土桥梁结构的建设具有重要意义[5-6]。

1 钢筋混凝土箱梁时变挠度计算的控制微分方程

1.1 考虑全截面剪切变形对梁挠度计算的影响

在竖向荷载作用下,由剪力引起的截面剪切变形使截面发生翘曲,进而引起梁的附加挠度。以变形前截面中性轴的交点为坐标原点,沿梁竖向和纵向分别为z轴和x轴,考虑剪切变形后梁体截面转角示意见图1。根据钢筋混凝土梁剪切变形原理,在竖向荷载作用下,任意时刻截面弯曲变形θ、剪切变形γ与挠度w之间的变化关系为[5]

图1 考虑剪切变形的梁截面转角示意

(1)

1.2 加载时刻翘曲位移函数的选取

在分析加载时刻混凝土箱梁剪力滞分布规律时,考虑到箱梁在竖向弯曲荷载作用下上、下翼缘板剪切变形的影响,在描述箱梁弯曲变形时,只采用广义挠曲位移函数w(x,t0)无法真实反映箱梁的真实弯曲变形,需再引入一个能够反映横截面变形的纵向翘曲位移函数u(x,y,z,t0)。在箱梁截面中,以中性轴的交点为坐标原点,沿梁纵向为x轴,箱梁纵向翘曲位移见图2。图2中,h1、h2、h3分别为箱梁顶板、悬臂板底板至箱梁中心轴的距离。根据箱形截面梁弯曲变形特点,结合文献[18],梁体各截面纵向翘曲位移函数u(x,y,z,t0)为

图2 箱梁纵向翘曲位移示意

u(x,y,z,t0)=hi[θ(x,t0)+fi(y,z)U(x,t0)]

(2)

式中:U(x,t0)为箱梁翼板剪切变形的最大差值;θ(x,t0)为加载时刻梁段弯曲变形;hi为箱梁各翼板中心至箱梁形心轴的距离;fi(y,z)为箱梁截面剪力滞翘曲位移函数。

单箱单室箱形截面梁见图3。图3中,b1、b2、b3、tw分别为箱梁顶板、悬臂板、底板及腹板的宽度;ts1、ts2、ts3、tsr分别为箱梁顶板、悬臂板、底板、腹板中钢筋等效厚度。

图3 单箱单室箱梁横截面示意

根据箱梁截面各翼板的构造特点和竖向荷载作用下各翼板剪切变形规律和剪力流分布规律[18-19],箱梁各翼板翘曲位移函数分别取为

(3)

式中:ξ2为箱梁悬臂板面积A2与顶板面积A1之比,ξ2=A2/A1;ξ3为箱梁底板面积A3与上翼板面积(A1+A2)之比,ξ3=A3/(A1+A2)。

1.3 长期荷载作用下混凝土应力应变关系

1.3.1t时刻混凝土应变和弯曲变形

根据CEB-FIP 2010[20],在单向不变荷载作用下,t时刻混凝土的总应变εct(t)可由加载时刻(t0时刻)混凝土弹性应变εc(t0)、徐变应变εcc(t)以及收缩应变εsh(t,tsh)组成,即

εct(t)=εc(t0)+εcc(t)+εsh(t,tsh)

(4)

式中:εct为t时刻混凝土的总应变;tsh为混凝土收缩开始时间。

图4 不同时刻混凝土应变与弯曲变形之间的关系

(5)

(6)

1.3.2 徐变系数

根据ACI209委员会建议,在单向不变荷载作用下,混凝土徐变系数φ(t,t0)可表示为t时刻混凝土徐变应变与弹性应变的比值[21],即

φ(t,t0)=εcc(t)/εc(t0)

(7)

式中:εc(t0)为加载时刻混凝土弹性应变;εcc(t)为t时刻混凝土徐变应变。

1.3.3t时刻混凝土应力应变关系

按照叠加原理,在t0时刻施加初应力σc(t0)后,又在t0至t时刻连续施加应力增量dσc的混凝土,之后t时刻混凝土总应变εct(t)为

J(t,t0)dτ+εsh(t,tsh)

(8)

J(t,t0)=[1+φ(t,t0)]/Ec

(9)

式中:J(t,t0)为混凝土徐变度;Ec为混凝土初始弹性模量。

研究结果表明,在线弹性范围内,混凝土徐变泊松比为常数,并等于瞬时弹性应变的泊松比[5,10],因此考虑时变效应后的混凝土应力应变关系可表示为

εct(t)=Aσc(t0)J(t,t0)+εsh(t,tsh)+

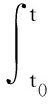
(10)

(11)

式中:μ为混凝土泊松比;εct(t)为t时刻混凝土应变列阵,εct(t)=[εx(t),εy(t),εz(t),γxy(t),γxz(t)γyz(t)]T,εx(t)、εy(t)、εz(t)分别为t时刻混凝土沿x、y、z方向的正应变,γxy(t)、γxz(t)、γyz(t)分别为t时刻混凝土沿xy、xz、yz平面的剪应变;σc(t0)为t0时刻混凝土应力列阵,σc(t0)=[σx(t0),σy(t0),σz(t0),τxy(t0),τxz(t0),τyz(t0)]T,σx(t0)、σy(t0)、σz(t0)分别为t0时刻混凝土沿x、y、z方向的正应力,τxy(t0)、τxz(t0)、τyz(t0)为t0时刻混凝土沿xy、xz、yz平面的剪应力;εsh(t,tsh)为混凝土收缩列阵。

为便于公式推导,将u(x,y,z,t0)、φ(t,t0)、J(t,t0)、εsh(t,tsh)、θ(x,t0)、θ(x,t)、w(x,t)分别简写为ut0、φ、J、εsh、θt0、θt、wt。

1.4 考虑徐变的剪力滞微分方程的建立

在应变能计算中,假定:①梁体各翼板竖向之间无挤压(εz≐0);②板平面外的剪切变形γxz与γyz以及横向应变εy均很小,可忽略不计[21];③混凝土材料收缩徐变特性不会对箱梁纵向应力分布形状产生影响,t时刻箱梁纵向位移函数与初始时刻保持一致[5]。则根据混凝土本构关系,在不计混凝土收缩徐变引起的应力增量情况下,t时刻混凝土的纵向应变εx(t)、剪切变形γxy(t)、弯曲变形θt可分别表示为

εx(t)=σx(t0)J+εsh=εx(t0)(1+φ)+εsh

(12)

γxy(t)=2(1+μ)τxy(t0)J=γxy(t0)(1+φ)

(13)

(14)

根据t0时刻混凝土箱梁纵向位移函数u(x,y,z,t0),利用几何方程可得t0时刻梁体任意截面任意位置混凝土正应变εix(t0)和剪应变γixy(t0)分别为[21]

(15)

(16)

式中:i=1,2,3;U′t0为箱梁翼板剪切变形最大差值的一阶导数。

将式(15)代入式(12),可得t时刻混凝土纵向应变为

εix(t)=(1+φ)hi[θ′t0+fi(y,z)U′t0]+εsh

(17)

将式(16)代入式(13),可得t时刻混凝土剪切变形为

γixy(t)=f′i(y,z)Ut0(1+φ)

(18)

结构体系的总势能定义为结构各部位总应变能与外力势能之差[21],即

(19)

各应变能和外力势能计算式分别如下:

1)翼板应变能

(20)

式中:V为梁段体积;Gc为混凝土初始剪切模量。

2)箱梁腹板应变能

(21)

式中:Ic4为腹板对形心轴的惯性矩;A4为腹板面积。

将式(14)代入式(21)后,可得t时刻箱梁腹板应变能为

(22)

3)钢筋应变能

(23)

式中:Es为钢筋弹性模量;εst(t)为考虑混凝土收缩徐变后钢筋的总横向应变,根据变形协调条件和几何方程[21],其表达式为

εist(t)=(1+φ)hi[θ′t0+fi(y,z)U′t0]

(24)

4)外力势能

(25)

结合式(14),梁体外力势能可改写为

(26)

将式(20)、式(22)、式(23)、式(25)代入式(19),可得体系总势能Π为

(27)

式中:K1=EcIc+EsIs;K2=EcIcu+EsIsu;K3=EcIcf+EsIsf;Ic=Ic1+Ic2+Ic3+Ic4;Is=Is1+Is2+Is3;Icu=3/4(Ic1+Ic2ξ2+Ic2ξ2);Isu=3/4(Is1+Is2ξ2+Is3ξ3);Icf=9/14(Ic1+Ic2ξ22+Ic3ξ32);Isf=9/14(Is1+Is2ξ22+Is3ξ32);Au=9/5(Ic1/b12+Ic2ξ22/b22+Ic3ξ32/b32);Ic、Is分别为箱梁全截面竖向弯曲惯性矩和翼板中钢筋对截面形心轴的惯性矩;Icu、Isu分别为翼板、翼板中钢筋剪滞翘曲惯性矩;Icf、Isf分别为翼板、翼板中钢筋剪滞翘曲惯性积;Au为翼板的剪滞翘曲面积;Sc为翼板对截面形心轴的静矩;Scf为翼板剪滞翘曲部分对截面形心轴的静矩;Ic1、Ic2、Ic3分别为箱梁顶板、悬臂板和底板对截面形心轴的惯性矩;Is1、Is2、Is3、Is4分别为箱梁顶板、悬臂板、底板和腹板中钢筋对截面形心轴的惯性矩。

根据最小势能原理[21],对式(27)进行变分运算,可得到t时刻徐变、收缩及剪力滞耦合作用下梁体控制微分方程和边界条件。得到的控制微分方程表达式为

(28)

边界条件为

(29)

式中:x1、x2分别为箱梁计算起始截面和终止截面的位置。

(30)

K1θ″t0=-K2U″t0-Q(x)

(31)

1.5 考虑徐变的剪力滞挠度求解

求解式(28),可得到纵向翘曲位移函数的通解为

(32)

式中:C1、C2为通解中的待定常数,可由边界条件式(29)确定。

通过对式(31)进行积分,可得初等梁理论计算的曲率θ′t0表达式为

(33)

整理式(28)第三式和式(33),可得梁体挠度为

wt=wt1+wt2+wt3+wt4+C4x+C5

(34)

值得注意的是,在不计收缩徐变效应后,式(34)可退化为用于加载时刻混凝土梁的挠度计算表达。与此同时,若忽略第二项wt2剪力滞效应和第四项wt4剪切效应后,式(34)将进一步退化为初等梁挠度理论解。

2 不同荷载作用下简支梁时变挠度计算理论解

2.1 简支梁承受均布荷载的挠度解

2.1.1 纵向翘曲位移

以跨径为l的混凝土简支箱梁承受满跨均布荷载q,见图5。

图5 简支梁承受满跨均布荷载

跨内任意截面承受的弯矩、剪力分别为

(35)

将式(35)代入式(32),可得

(36)

引入式(29),可得简支梁承受均布荷载作用时截面纵向翘曲位移为

(37)

2.1.2 挠度计算理论解

将式(35)和式(37)代入式(33),并引入式(29),可得梁体曲率θ′t0的表达式为

(38)

通过整理式(34)、式(35)、式(37)、式(38),并引入边界条件wt(x=0)=0和wt(x=l)=0,可得梁体挠度为

(39)

2.2 简支梁承受集中荷载的挠度解

2.2.1 纵向翘曲位移

混凝土简支箱梁承受集中荷载P,布置见图6。跨内任意截面承受的弯矩、剪力可用式(40)所示的分段函数表示,即

图6 简支梁承受集中荷载

(40)

将式(40)代入式(32),由边界条件

(41)

整理可得截面纵向翘曲位移为

(42)

2.2.2 挠度计算理论解

将式(40)和式(42)代入式(33),并引入边界条件式(29),可得左半部分梁体曲率表达式为

(43)

通过整理式(34)、式(40)、式(42)和式(43),并引入边界条件wt(x=0)=0和w’t(x=l/2)=0,可得梁体左半部分挠度计算式为

(44)

3 算例分析

选取文献[23]中跨径为24 m的UHPC简支箱梁作为算例,其截面尺寸及配筋见图7。UHPC立方体抗压强度fck为120 MPa,棱柱体抗压强度fcm为88 MPa,抗拉强度fct为6 MPa,弹性模量为4.4×104MPa,泊松比μ为0.2。钢筋N1～N11均采用直径为10 mm的HPB300钢筋,其弹性模量为210 GPa,泊松比为0.3,抗拉压强度为270 MPa。假定在UHPC龄期为4 d时对UHPC简支箱梁进行加载,荷载作用形式见图8。根据DBJ 43/T 325—2017《活性粉末混凝土结构技术规程》[24],UHPC徐变系数和收缩应变在加载50 a内的发展情况见图9。

图7 箱梁1/2横截面及配筋示意图(单位:cm)

图8 荷载作用示意

图9 UHPC和NC徐变系数与收缩应变随时间的变化

采用有限元分析软件Midas Civil建立上述UHPC简支箱梁的三维有限元分析模型,其中UHPC采用8节点实体单元模拟,钢筋采用梁单元模拟。忽略钢筋与混凝土之间的黏结滑移,钢筋与混凝土之间采用共节点的连接方式。建立的有限元模型见图10。

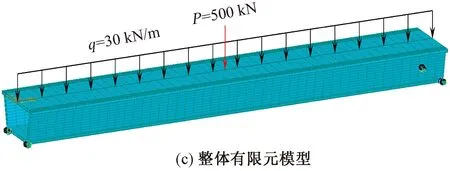
图10 UHPC简支箱梁有限元模型

3.1 加载时刻UHPC简支箱梁挠度分析

为对比剪力滞效应和剪切效应对简支梁挠度计算的影响,运用本文理论计算方法和有限元模拟方法计算得到了加载时刻UHPC简支梁挠度曲线,结果见图11,为对比分析不同计算方法的影响,分别按下述方法计算:①初等梁理论计算结果,即不考虑剪切变形和剪力滞效应影响的挠度,简称EBT;②初等梁理论计算结果的基础上考虑剪切变形影响后计算所得挠度,简称EBL;③初等梁计算结果的基础上考虑剪切效应后计算所得挠度,简称EBS;④初等梁理论计算结果的基础上同时考虑剪切变形和剪力滞效应后计算所得的挠度,简称ELS;⑤有限元模拟结果,简称FEA。

图11 不同计算方法计算的简支梁挠度曲线

由图11可知,在不同荷载作用下,运用本文理论公式计算的UHPC简支梁总挠度与有限元模拟值之间吻合良好,最大挠度之间偏差小于1%。不同分析方法得到的挠度均由跨中向两侧支点递减。在均布荷载(集中荷载)作用下,考虑剪切效应后产生的挠度明显大于考虑剪力滞效应产生的挠度,在跨中截面两者之间偏差最大,与按初等梁理论计算得到的跨中挠度相比,分别增大了7.6%(9.5%)和1.8%(1.4%),说明箱梁剪切效应对挠度计算的影响大于剪力滞效应。在同时考虑剪力滞效应和剪切效应的情况下,简支梁跨中挠度分别是初等梁挠度的1.09倍(均布荷载)和1.11倍(集中荷载),表明剪力滞和剪切效应对简支梁挠度计算存在影响,在箱梁挠度计算时应予以考虑。

3.2 长期荷载作用下UHPC简支箱梁挠度分析

为描述UHPC收缩徐变对结构附加挠度的影响,在上述ELS分析的基础上考虑收缩徐变对UHPC简支箱梁长期性能的影响,采用本文计算方法对不同荷载作用下UHPC简支箱梁长期性能进行分析。按不同计算方法计算得到的UHPC简支箱梁加载50 a后的挠度曲线和跨中最大挠度随时间的变化见图12,图12中,ELSSC代表ELS+收缩徐变效应分析。

图12 收缩徐变对简支箱梁挠度的影响

由图12(a)可知,不同荷载作用下,考虑收缩徐变效应后产生的挠度与加载时刻瞬时挠度沿桥梁跨度方向的分布规律一致,均由跨中向两侧支点递减。在均布荷载(集中荷载)作用下,考虑收缩徐变效应后产生的挠度明显大于加载时刻瞬时挠度,尤其是在跨中截面,两者之间偏差最大,是加载时刻瞬时挠度的2.52倍(2.57倍)。说明收缩徐变效应对UHPC简支梁长期挠度计算影响较大。

由图12(b)可知,在不同荷载作用下,考虑收缩徐变效应计算得到的简支梁跨中挠度随服役时间的增加而增大,在加载初期,挠度增长速率较快,后期增长速率较慢,这主要是由于UHPC收缩徐变效应在加载初期发展较快,后期发展较慢引起的。

由图12可知,不同荷载作用下,考虑收缩徐变效应后产生的挠度随截面位置和时间的变化与有限元模拟结果一致,二者吻合良好。

3.3 截面配筋对UHPC简支箱梁长期性能的影响

在上述ELSSC分析的基础上,对比分析了截面配筋对简支梁短、长期挠度计算的影响。简支梁在不同荷载作用下,按不同分析工况计算得到的简支梁挠度曲线见图13。图13中,CR代表考虑截面配筋;NCR代表不考虑截面配筋;t0和t分别代表加载时刻和分析终止时刻,t0=0、t=50 a。

图13 配筋对简支梁挠度计算的影响

由图13可知,不同荷载作用下,不考虑配筋后计算得到的短、长期挠度与考虑配筋后计算得到的短、长期挠度沿跨度方向的分布规律一致,均由跨中向两侧支点递减。考虑截面配筋后计算得到的箱梁短、长期挠度明显小于不考虑配筋后的挠度,特别是在跨中截面,两者之间偏差最大。与不考虑截面配筋后计算得到的箱梁短、长期挠度相比,考虑截面配筋后跨中短期挠度分别减小了4.3%(均布荷载)和4.2%(集中荷载),长期挠度分别减小了11.0%(均布荷载)和10.6%(集中荷载)。可见考虑截面配筋对简支梁长期挠度的影响大于加载时刻瞬时挠度的影响。表明截面配筋对简支箱梁短、长期挠度计算影响较大,在计算时应予以考虑。

不同荷载作用下,按不同分析工况计算得到的简支梁跨中挠度的时程曲线,见图14。由图14可知,不同荷载作用下,考虑与不考虑截面配筋后计算得到的箱梁跨中挠度均随时间的增加而增大,在加载初期,挠度发展速率较快,后期发展较慢。考虑截面配筋后计算得到的跨中挠度明显小于不考虑截面配筋后得到的箱梁跨中挠度,且随服役时间的增大,两者之间的偏差逐渐增大,服役时间从t0增加到t时,两者之间偏差分别增大了7.9%(均布荷载)和7.5%(集中荷载),表明截面配筋对箱梁长期挠度的影响随时间的增加而增大。这是由于随着服役时间的推移,UHPC弹性模量逐渐减小而钢筋弹性模量不变引起的。

图14 简支梁跨中挠度随时间的变化

3.4 UHPC与NC材料特性对结构长期挠度的影响

在上述ELSSC分析的基础上,考虑截面配筋的影响,采用上述推导的简支梁挠度理论计算公式,对满足设计要求,且具有相同计算参数、截面形式以及边界条件的UHPC梁和普通混凝土(NC)梁长期性能进行了分析。NC梁采用C50混凝土。根据TB 10092—2017《铁路桥涵混凝土结构设计规范》[25],C50混凝土极限抗压强度和弹性模量分别取33.5、3.55×104MPa,泊松比取0.2,收缩徐变系数在50 a内的发展见图9。利用理论公式计算了不同荷载作用下NC梁和UHPC梁跨中挠度曲线,结果见图15。不同时刻NC梁和UHPC梁跨中挠度计算结果见表1。

表1 不同时刻UHPC梁和NC梁跨中挠度的对比

图15 UHPC梁和NC梁跨中挠度随时间的变化

由图15和表1可知,与不同荷载作用下NC梁跨中挠度相比,采用UHPC材料后简支梁跨中瞬时加载挠度减小了18.5%,长期挠度减小了41.2%,说明采用UHPC材料可有效减小梁的短、长期挠度。均布荷载作用下,考虑收缩徐变效应后的NC和UHPC梁跨中挠度相比于加载时刻瞬时挠度分别增大了254.6%和155.8%,集中荷载作用下分别增大了255.9%和156.6%。表明UHPC材料在减小简支梁短、长期挠度以及收缩徐变引起的挠度变化方面具有良好的抑制效果。

4 结论

本文综合考虑箱梁剪切效应、剪力滞效应以及收缩徐变效应的影响,对长期荷载作用下UHPC简支箱梁挠度进行了计算与分析。通过分析可得出如下结论:

1) 通过UHPC简支箱梁算例计算结果表明,利用本文理论公式计算的箱梁挠度与有限元模拟结果吻合良好;推导的简支梁挠度计算公式简单,物理意义明确,利用公式不仅能计算加载时刻瞬时挠度,还能计算UHPC简支梁的长期挠度。

2) UHPC简支箱梁短期挠度计算结果表明,在均布荷载和集中荷载作用下,考虑剪力滞效应后计算得到的简支梁跨中挠度分别是初等梁挠度的1.02倍和1.01倍;考虑剪切效应后计算得到的简支梁跨中挠度分别是初等梁挠度的1.08倍和1.10倍。说明剪力滞和剪切效应对简支梁挠度计算的影响不可忽略,且剪切效应的影响明显大于剪力滞效应。

3) UHPC简支箱梁长期挠度计算结果表明,收缩徐变效应是导致UHPC简支梁长期挠度增大的主要原因。在均布荷载作用和集中荷载作用下,考虑UHPC收缩徐变效应后产生的跨中挠度分别是加载时刻瞬时挠度的2.52倍和2.57倍。

4) 考虑截面配筋后计算得到的箱梁短、长期挠度明显小于不考虑配筋后的挠度,特别是在跨中截面,两者之间偏差最大。均布和荷载作用下,考虑配筋后箱梁短、长期挠度均分别是不考虑配筋时的0.96、0.89倍。

5) 与NC梁挠度计算结果对比表明,采用UHPC材料代替NC材料可显著降低结构的长期挠度。在计算参数相同的情况下,UHPC梁的短、长期挠度分别是NC梁短、长期挠度的0.82、0.59倍。