车辆-轨道非线性耦合系统显隐式求解算法的收敛性分析

秦佳良，刘林芽，2

(1.华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013；2.萍乡学院 工程与管理学院，江西 萍乡 337055)

铁路交通是国家发展的重大公共基础设施,是现代化综合交通运输体系的基础骨干,对促进经济社会的快速发展起到了十分显著的作用。我国在进入21世纪以来,在高速铁路、重载铁路、城市轨道交通等领域取得了世界瞩目的成就。轨道交通通过轮轨相互作用来实现其功能,保持轨道良好的平顺性,降低机车车辆对轨道和轨下基础的动力作用,减少养护维修的成本,以及新型机车车辆和新型轨道结构的设计、制造等问题的解决都需要对车辆与轨道系统之间相互作用的动力特性展开深入研究[1]。因此准确、高效地求解车辆-轨道耦合系统的动态响应对保证轨道交通的可持续发展具有重大的理论和现实意义。

车辆-轨道耦合系统的动力响应模型求解一直是车辆动力学和轨道动力学研究中最关键的基础问题[2]。近几十年以来,国内外众多学者曾先后对车辆-轨道耦合作用引起的机车车辆、轨道结构、路基、隧道、桥梁及大地振动等方向展开了深入的研究[3-7],提出一系列繁简各异的轮轨动力学理论、算法、模型、程序及软件,部分实现了工程应用,有效地解决了在轨道交通可持续发展中面临的一些瓶颈问题,也取得了一些较为显著的研究成果[8-12]。在一般应用情况下,车辆-轨道耦合系统的动力学分析模型较复杂且动力自由度数目也较多,采用解析法直接分析和求解其动力学微分方程组会十分复杂且困难,因此目前一般都普遍采用直接数值积分法来求解。直接数值积分法分为显式数值积分法和隐式数值积分法两种不同的形式。隐式数值积分法一般具有稳定性较好、计算的精度较高等特点,普遍使用的隐式数值积分法一般包括Newmark-β法、Wilson-θ法、Park法和Hobolt法等。但隐式数值积分法每步积分均需求解大型代数方程组,这对计算规模大的工程问题带来了巨大的挑战。与隐式数值积分法不同,显式数值积分法则一般具有计算过程较简单、计算效率较高等一些优点,普遍使用的显式数值积分法一般包括新型快速显式积分法、四阶Runge-Kutta法和中心差分法等。显式数值积分法明显的缺点就是其稳定性或计算精度一般比隐式数值积分法略差。可见,显式数值积分与隐式数值积分的优缺点是互补的。鉴于此,我们在求解车辆-轨道非线性耦合系统振动方程时,尝试将显式数值积分与隐式数值积分联合使用,以期获得比较好的综合性能。

本文利用有限元法分别建立了车辆子系统和轨道子系统的动力学分析模型,然后采用显式数值积分法和隐式数值积分法分别求解车辆子系统和轨道子系统的动力学方程,提出了车辆-轨道非线性耦合系统振动分析的分离迭代和分离同步两种求解方法,并对两种方法进行了算例验证。最后通过进一步研究时间步长对轮轨耦合系统振动响应的影响,以及对比不同时间步长下车辆-轨道非线性耦合系统的数值计算效率,分析两种算法在计算稳定性、准确性和数值编程求解效率等方面的差异,为求解车辆-轨道非线性耦合相互作用问题提供可供选择的高效数值计算方法。

1 车辆-轨道非线性耦合系统动力学方程

本文建立车辆-轨道非线性耦合系统分析模型时,由于车辆子系统和轨道子系统沿线路方向左右对称,因此本文只取半结构展开研究。且本文仅考虑轮轨竖向动力效应,轮轨间考虑为Hertz非线性接触。

1.1 车辆子系统动力学方程

车辆子系统可以考虑为一个10自由度的具有一、二系悬挂的整车模型,模型分别考虑车体、转向架的沉浮和点头运动以及轮对的沉浮运动,具体情况见图1。图1中,Mc、Jc分别为车体的质量、转动惯量;Mt、Jt分别为转向架的质量、转动惯量;Mwi(i=1,2)为第i个车轮的质量;Ks1、Cs1分别为车辆的一系悬挂刚度、阻尼;Ks2、Cs2分别为车辆的二系悬挂刚度、阻尼;νc、νti(i=1,2)分别为车体、前后转向架沉浮运动的竖向位移;θc、θti(i=1,2)分别为车体、前后转向架点头运动的角位移;νwi(i=1,2,3,4)为第i个车轮沉浮运动的竖向位移;l1、l2分别为车辆固定轴距之半、车辆定距之半。

车辆子系统的位移向量XV为

XV={vcθcvt1θt1vt2θt2vw1vw2vw3vw4}T

(1)

由Lagrange方程我们可以直接得到车辆子系统的动力学方程为

(2)

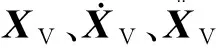
QV=-g{Mc0Mt0Mt0MwMwMwMw}T

(3)

FVT={0 0 0 0 0 0F1F2F3F4}T

(4)

式中:g为重力加速度;Fi(i=1,2,3,4)为轮轨相互用力,可用Hertz非线性弹性接触理论来计算,其表达式为

(5)

其中,νlci、ηi(i=1,2,3,4)分别为第i个轮轨接触处的钢轨位移、轨道的不平顺幅值;G为轮轨接触常数[5]。

1.2 轨道子系统动力学方程

以路基上采用的CRTS Ⅱ型板式无砟轨道结构为例,建立模拟板式无砟轨道子系统的动力学分析模型。针对CRTS Ⅱ型板式无砟轨道子系统结构形式的特点,将轨道子系统沿线路纵向取半结构进行分析研究,并利用有限元法来模拟板式无砟轨道子系统。将沿线路纵向两相邻扣件之间的轨道结构考虑为一个板式无砟轨道单元,单元长度记为l,单元模型见图2。模型中,将钢轨模拟为离散黏弹性点支承梁单元,Ky1、Cy1分别为扣件的弹性系数、阻尼系数;将轨道板和底座板模拟为连续黏弹性支承梁单元,Ky2、Cy2分别为CA砂浆层的弹性系数、阻尼系数,Ky3、Cy3分别为路基层的弹性系数、阻尼系数。图2中,ν1、ν4分别为钢轨两端的竖向位移;θ1、θ4分别为钢轨两端的转角;ν2、ν5分别为轨道板两端的竖向位移;θ2、θ5分别为轨道板两端的转角;ν3、ν6分别为底座板两端的竖向位移;θ3、θ6分别为底座板两端的转角。

图2 板式无砟轨道单元模型

(6)

(7)

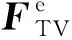
最后利用有限元法的“对号入座”法则,根据板式无砟轨道单元的质量矩阵、阻尼矩阵和刚度矩阵,组集整个轨道子系统的质量矩阵、阻尼矩阵、刚度矩阵,可得到轨道子系统的动力学方程为

(8)

2 显隐式求解算法计算流程

在用数值方法求解车辆-轨道非线性耦合系统分析模型的动力学方程时,因车辆子系统的质量矩阵为对角阵,数值计算时可以采用新型显式积分法来求解车辆子系统的动力学方程;轨道子系统采用有限元法建立,其质量矩阵为非对角阵,数值计算时可以采用Newmark-β积分法来求解轨道子系统的动力学方程。分别建立车辆-轨道非线性耦合系统振动分析的分离迭代和分离同步两种求解方法。分离迭代法是将车辆-轨道非线性耦合系统划分为车辆和轨道两个非时变的子系统模型,通过轮轨位移协调或轮轨力平衡关系将两个子系统模型联系起来,两个子系统模型之间通过迭代计算来分别求解车辆子系统模型和轨道子系统模型的动力学方程。分离同步法其实也是将车辆-轨道非线性耦合系统分析模型划分为车辆和轨道两个非时变子系统模型,但车辆子系统模型和轨道子系统模型的动力学方程是同步求解的,不需要进行迭代求解。

2.1 显隐式积分求解格式

(9)

(10)

式中:Δt为时间积分步长;ψ、φ分别为控制积分方法特性的两个独立参数,计算起步时只需令ψ=φ=0。

(11)

(12)

(13)

式中:c0=1/(αΔt2);c1=δ/(αΔt);c2=1/(αΔt);c3=1/(2α)-1;c4=δ/α-1;c5=Δt(δ/α-2)/2;c6=Δt(1-δ);c7=δΔt;Newmark-β积分常数α和δ分别取0.25和0.5。

2.2 显隐式分离迭代法求解流程

在开始求解时先假设车辆子系统和轨道子系统从静止起步,即初始时刻t=0时,车辆子系统和轨道子系统的位移响应、速度响应和加速度响应均为零。在对时间步长进行循环计算时,假设在t+Δt时刻,两个子系统动力学方程求解已进行k次迭代,现在考察第k+1次迭代。

当k为偶数时,令

(14)

并计算差值Δ1(i)为

(15)

当k为奇数时,令

(17)

注意到Aitken加速法是每迭代两次才改善一次。

Step6根据轨道子系统位移差值Δ进行收敛性判别,即

(18)

收敛条件为

(19)

Step7如果计算满足收敛性,则可以转入下一时间步长后继续循环计算,直至整个时域T。如果计算不满足收敛性,则令k=k+1,进入下一迭代步后继续循环计算。

为进一步提高显隐式分离迭代法的计算效率,参照文献[14]中的改进方法,根据式( 9 )、式(10)和式(11),可以在迭代步循环计算前,先计算车辆子系统的位移和速度,以及轨道子系统位移响应在迭代步循环过程中的不变量,在迭代求解过程中直接调用即可,这样可以减少计算工作量。

2.3 显隐式分离同步法求解流程

与显隐式分离迭代法一样,显隐式分离同步法在开始求解时车辆子系统和轨道子系统也从静止起步,即假设初始时刻t=0时,车辆子系统和轨道子系统的位移响应、速度响应和加速度响应均为零。现假设已经求得t-Δt和t时刻车辆子系统和轨道子系统的位移响应、速度响应和加速度响应,现在需要求解t+Δt时刻两个子系统的位移响应、速度响应和加速度响应。主要计算步骤如下:

3 显隐式求解算法验证

为验证本文提出的显隐式分离迭代法和显隐式分离同步法的正确性,与文献[15]中计算的算例进行比较。计算条件为假设列车编组为1动+1拖的高速列车在博格板式无砟轨道上运行,运行速度为200 km/h,轨道高低不平顺激振源考虑成波长为20 m、波幅为6 mm的周期性正弦函数,其计算结果见图3,文献[15]的计算结果见图4。

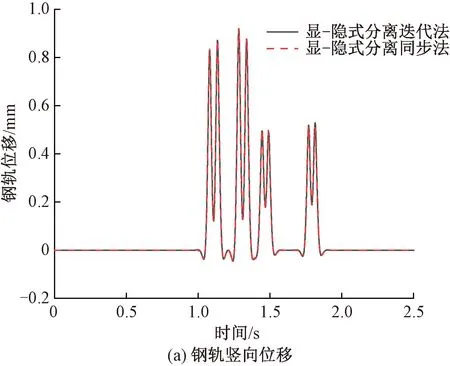
图3 本文计算结果

图4 参考文献[15]中计算结果

由图3和图4的计算结果对比可知,钢轨和博格板的位移响应波形均符合物理概念,与文献[15]计算得到的响应幅值与变化规律基本一致,证明了本文提出的显隐式分离迭代法和显隐式分离同步法的正确性和可行性。

4 显隐式求解算法收敛性对比分析

本文为对比分析显隐式分离迭代法和显隐式分离同步法的收敛性,以CRH3型高速动车通过CRTSⅡ型板式无砟轨道为计算算例。其中车辆的运行速度设置为300 km/h,板式无砟轨道单元的长度取0.65 m,在进行数值计算时轨道子系统的长度设为360个轨道单元的长度。轨道高低不平顺设置为车辆-轨道非线性耦合系统的激励源,将其考虑成波长为12.5 m、波幅为3 mm的周期性正弦函数。车辆子系统和轨道子系统的结构参数按照文献[16]中的参数取值。

4.1 时间步长的确定

在应用中最为重要的问题就是时间步长的确定,这直接影响到数值计算是否收敛以及计算效率。我们采用数值试验方法,对各种时间步长(最小时间步长为10-3ms)进行了数值模拟,计算结果见图5、图6。

图5 轮轨振动加速度的数值模拟结果

图6 轮轨力的数值模拟结果

由图5和图6可知,时间步长对轮对加速度和轮轨力的影响相对较小,而对钢轨加速度的影响较大。显隐式分离迭代法的临界收敛时间步长为1 ms,超过1 ms后计算结果将不收敛,最大有效时间步长可取为0.5 ms。显隐式分离同步法的临界收敛时间步长和最大有效时间步长均为0.1 ms,超过0.1 ms后计算结果将不收敛。

4.2 计算效率的对比分析

为对比显隐式分离迭代法和显隐式分离同步法在计算效率上的差异,在计算机上运行程序,计算时间步长分别取0.5、0.1、0.05、0.01 ms时,考察两种方法的计算耗时。不同时间步长下车辆-轨道非线性耦合系统的求解时间见表1。

表1 不同时间步长耦合系统求解时间

由表1可知,采用显隐式分离迭代法求解时,当时间步长取得较大时,采用Aitken加速法可以增强系统迭代求解的计算稳定性,但当时间步长取得越小,Aitken加速法的作用会越来越小。这是因为当时间步长较大时,耦合系统在下一时刻的平衡状态会和上一时刻耦合系统的平衡状态产生严重偏离的情况,这将导致耦合系统数值解的发散而使得计算结果无法收敛,或者耦合系统需要多次迭代才能使计算结果收敛,此时采用Aitken加速法可以减少迭代次数,可以起到增强迭代计算稳定性的作用。而当时间步长取得越小时,耦合系统在下一时刻的平衡状态会和上一时刻耦合系统的平衡状态越接近,这会使得耦合系统非常容易地再次达到其平衡位置,因此耦合系统的收敛速度会较快且Aitken加速法的作用会越来越小。

当采用相同时间步长时,显隐式分离同步法的计算效率要比显隐式分离迭代法更高。这是因为采用显隐式分离迭代法求解时,每一时间步内车辆子系统和轨道子系统的动力学方程至少分别求解2次才能收敛,而采用显隐式分离同步法求解时每一时间步内只需求解一次耦合系统的动力学方程,因此显隐式分离同步法的计算效率会更高。但是显隐式分离迭代法可以通过选取较大的时间步长来提高耦合系统的计算效率,在实际工程应用时可根据实际情况选用合适的求解方法。

5 结论

1)提出了基于显隐式积分格式的车辆-轨道非线性耦合系统分离迭代和分离同步两种数值计算方法,并通过算例验证了两种算法的正确性。

2)对车辆-轨道非线性耦合系统进行数值分析时,显隐式分离迭代法和显隐式分离同步法的最大有效时间步长分别是0.5、0.1 ms。

3)当时间步长较大时,采用Aitken加速法可以起到增强显隐式分离迭代法的计算稳定性的作用。但随着时间步长的减小,Aitken加速法的作用会越来越小。

4)相同时间步长下显隐式分离同步法的计算效率要比显隐式分离迭代法高,但是可以采用较大的时间步长来提高显隐式分离迭代法的计算效率。