高速列车纵向动力学建模与自适应RBFNN控制
付雅婷,胡东亮,杨 辉,欧阳超明
(1.华东交通大学 电气与自动化工程学院,江西 南昌 330013;2.华东交通大学 轨道交通基础设施性能检测与保障国家重点实验室,江西 南昌 330013;3.中国铁路广州局集团有限公司,湖南 长沙 410001)
随着社会的快速发展,高速列车作为一种快速、高效的运输工具越来越受到人们的欢迎,已然成为了现代交通运输体系中不可或缺的部分。然而由于高速列车运行速度快,运行环境复杂多变,工况变化频繁[1],且系统容易受到内部以及外界各种未知干扰的影响,呈现出快时变、强非线性的特点,而目前的人工驾驶不受过多约束,驾驶效果仅依赖于驾驶员的操作经验和技术,且复杂的路况和外界各种未知干扰将会影响人工驾驶的性能(平稳性和高效性等),因此设计使高速列车既能可靠高效运行,又能对目标速度位移进行高精度追踪的列车自动驾驶(ATO)系统仍然具有很大挑战。为设计安全高效的ATO系统,需要从高速列车的建模方法及控制策略两个方向进行探索。
目前关于列车的动力学模型大致分为单质点模型和多质点模型。单质点模型忽略了列车的车间耦合关系,将列车简化为一个刚性质点进行受力分析,这种模型结构简单,被广泛应用于列车控制算法的研究中。目前被广泛认可的单质点模型是由Khmelnitsky[2]及Howlett等[3]所建立的模型,而后来的学者大多是根据需求在该模型上进行改进。文献[4]根据城轨列车运行仿真对快速性和实时性方面的要求,对传统单质点模型进行了改进,提高了其实时计算效率和计算精度。文献[5]考虑了高速列车运行过程中会受到外界未知干扰的影响,建立了含有干扰的列车单质点模型,但是其为简化仿真过程,忽略了列车受到的附加阻力。这种单质点建模[6-8]方法是对列车整体运行状态的宏观描述,而对于列车车厢之间的车钩作用力以及各节车厢的牵引力和制动力分配情况不能进行准确的描述,尤其是当高速列车行驶到复杂路况(如弯道、坡道、隧道)时,车厢间的车钩链接作用就会被凸显,单质点建模方法就会失去准确性。文献[9-10]将两车厢间车钩力看作为列车的内力,采用一种“多质点-单位移”模型,但这种方法也是只能对列车的整体运行状态进行描述,而对于各节车厢的运行状态并不能准确描述。文献[11-12]将链接车厢的车钩看作弹性部件,用相邻两车厢位移偏差的非线性函数来表示车钩力,建立了列车的多质点模型,但其为了方便控制器的设计,认为非线性空气阻力只作用于列车的车头,其他车厢只考虑包含基本阻力的线性部分。文献[13]引入了列车运行状态整数变量,建立了高速列车混合多质点模型,但是其将列车基本运行阻力进行了分段线性化处理,一定程度上降低了模型的准确性。因此,基于高速列车车钩链接的特点,考虑车厢之间的受力与运行线路情况,建立高速列车纵向动力学模型,将能够更准确全面地描述高速列车整列车的运行过程。
同时,为了实现对高速列车的运行优化控制,众多学者提出了许多不同的解决方案,主要有自适应控制、预测控制、滑模控制、模糊控制或多种控制方法的结合[14-17]。文献[18]提出了模糊-PID控制方法,该方法旨在解决速度控制时PID控制器切换次数过多的问题,采用基于模糊规则的切换方式来提高列车运行的平稳性,然而未考虑真实路况及未知干扰对列车运行的影响。文献[19]基于自适应迭代学习方法提出一种高速列车容错控制算法,能够解决时滞、执行器故障下的高速列车跟踪控制问题,但该方法要取先前的列车运行信息作为当前调整策略的依据,需要足够多的数据和迭代次数,才能获得好的控制精度,并且不能处理外界随机出现的未知干扰。文献[20]提出一种分布式神经网络滑模控制方法,该方法同文献[21]一样,对处理模型非线性部分和未知外界干扰具有很好的控制效果,但控制方法本身因具有切换项会使输出有抖振的情况发生,会降低控制器的寿命,加剧车钩的磨损,也未考虑真实路况对列车运行的影响。文献[22]结合反演法和滑模控制设计了一种反演滑模控制方法来解决列车运行过程中的简单路况变化及不确定扰动, 虽然该方法提高了列车的跟踪控制精度,但由于其引入了滑模控制而会出现控制力抖振的问题,并且在应对列车复杂附加阻力时没有更好的控制效果。
综上所述,针对目前高速列车控制方法对于处理列车运行于复杂路况变化及遭受外界未知扰动时控制效果不佳的问题,本文在考虑了由车钩链接而成的纵向动力学模型基础上,根据高速列车动力相对分散的特点[23]提出了一种自适应径向基函数神径网络(rad-ial basis function neural network,RBFNN)控制方法。该方法对于给定目标速度、位移具有较高的跟踪精度,且在处理比较复杂的路况变化以及外界未知扰动时具有更好的控制性能和更快的稳定速度,能够提升控制器的工作寿命和降低车钩的磨损速度,有利于提升高速列车运行过程的平稳性和高效性。
1 高速列车纵向动力学模型
本文以CRH380B型[24]高速列车为例,它是由8节车厢编组而成的高速列车,其中第1、3、6、8节车厢为能提供动力的动车,第2、4、5、7节车厢为拖车。CRH380B型高速列车各节车厢的编号分别为EC01、TC02、…、EC08,具体见图1。

图1 CRH380B型高速列车编组
图1中,黑色轮子的车厢表示此车厢是装备有牵引动力单元的动车,而白色轮子的车厢为拖车。为准确描述该高速列车的纵向动力学模型,需要对单节车厢进行受力分析,以第i节车厢为例,其受力情况见图2。

图2 高速列车单节车厢受力分析
图2中,ui为第i节车厢所受牵引力或制动力,由于只有动力车厢提供牵引力或制动力,故当该车厢为拖车时ui=0;fCi-1_i为该车厢受到的前车车钩力;fCi_i+1为该车厢受到的后车车钩力;fw0i为该车厢受到的基本阻力;fwQi为该车厢受到的附加阻力。
1.1 列车阻力
1.1.1 基本阻力
高速列车在行进过程中会受到阻碍列车前进的基本阻力(如滚动阻力和空气阻力)。其在起动时单位基本阻力为5 N/kN;而在运行中的单位基本阻力w0一般是通过经验公式[25]得到,即
(1)

1.1.2 附加阻力
附加阻力[26]是列车运行在不同的路况(如坡道、弯道、隧道等)而受到的额外阻力。列车在行进过程中,存在不同的车厢运行在不同路况的情况,为准确描述列车模型,需考虑列车长度对列车所受到附加阻力的影响。
1)坡道附加阻力
在计算坡道附加阻力时,列车纵向动力学模型存在不同车厢位于不同坡道的情况。为准确描述这种情况,需要对列车在坡道上的分布情况进行分析,图3为高速列车行驶到某变坡道上的纵向动力学模型坡道附加阻力分析。

图3 高速列车纵向动力学模型坡道附加阻力分析
图3中,L1、L2分别为列车在坡道1、2上的长度,m。θ1、θ2分别为两个坡道的坡道千分数;行驶在坡道1上的车厢所受到的单位坡道阻力wpi=θ1,行驶在坡道2上的车厢所受到的单位坡道阻力wpi=θ2,N/kN。
2)曲线附加阻力
与坡道阻力相似,列车车厢行驶在不同的弯道时受到的弯道阻力也不尽相同,同理需要分开进行计算。假设列车行驶到两个不同的弯道,在弯道1、2上面的列车长度分别为S1、S2,列车的总长度L=S1+S1,m。R1、R2分别为弯道1、2的曲线段的半径,m;则行驶在弯道1上的车厢所受到的单位曲线附加阻力[27]wri=H/R1,行驶在弯道2上的车厢所受到的单位曲线附加阻力wri=H/R2,N/kN,其中H为常数,一般取600。
3)隧道附加阻力
同理,对于高速列车纵向动力学模型的隧道附加阻力wsi的计算也需考虑车身长度的影响,因为列车在通过隧道时存在有一部分车厢在隧道里和一部分车厢在隧道外的情况。假设在隧道里和隧道外的列车长度分别为Yi1、Yi2,而列车的总长度为L,隧道的长度为Ls,m,则此时在隧道内的列车所受到的单位隧道附加阻力wsi[27]为
(2)
综上所述,高速列车第i节车厢在运行时所受到的总单位附加阻力wQi[27]为
wQi=wpi+wri+wsi
(3)
1.1.3 车钩力
将高速列车的每节车厢看作一个质点进行分析,还需考虑车厢间的相互作用力,即车钩力。将高速列车车厢间的车钩力简化为一个“弹簧-阻尼器”系统,见图4。

图4 车钩作用原理
第i节与第i+1节车厢之间的车钩作用力fCi_i+1的表达式可描述为

(4)

1.2 高速列车纵向动力学模型的建立
高速列车在运行过程中,存在有车厢之间人员流动的情况,将会导致列车各节车厢的质量处在一个相对稳定变化的过程中。为考虑这种情况存在,根据前面所述列车模型为多质点时的列车阻力及车钩力的计算方法,并结合牛顿运动学定律,高速列车纵向动力学模型方程为
(5)

2 高速列车自适应RBFNN控制器设计
高速列车纵向动力学模型能够更准确地描述列车的运行过程,但随着列车运行速度的不断加快,系统的非线性会进一步增加,再加上车钩系统的存在,会使整个系统的复杂度上升,这些都会提高列车控制器的设计难度,而目前RBF神经网络控制对于复杂系统控制问题展现出了较好的效果,为实现高效可靠控车的目的,本文设计了一种基于理想反馈控制的RBF神经网络控制,同时采用了神经网络最小参数学习法,通过设计参数估计自适应律来代替神经网络的调整,加快RBF神经网络的学习速度,减小计算量。本文设计的高速列车自适应RBF神经网络控制的闭环结构框图见图5。
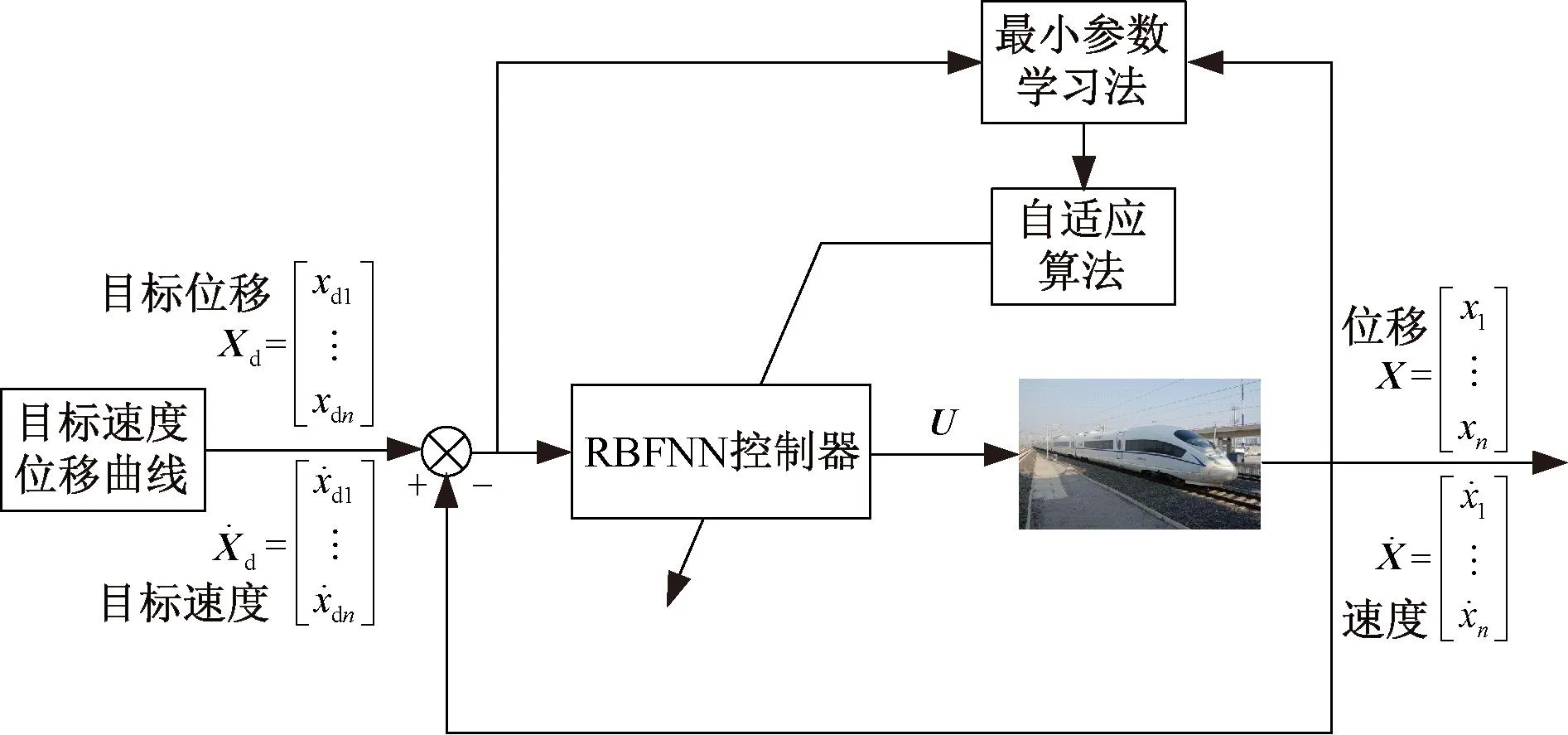
图5 高速列车自适应RBFNN控制框图

2.1 系统描述
将式( 5 )改写成式( 6 ),并结合其结构特点,设计了一种基于RBF神经网络的直接鲁棒自适应控制器。
(6)
s.t.
G(xi)=βi/(mi+Δmi)

定义滑模误差函数为
(7)
式中:si为第i节车厢的误差函数,参数λi>0,从而多项式si+λi是满足Hurwitz。
对式( 7 )中si求导,可得
(8)

2.2 控制器设计
2.2.1 理想反馈控制律设计
(9)

(10)
则有
(11)


(12)
其中,紧集Ωzi定义为
(13)

2.2.2 RBF神经网络的逼近
RBF神经网络是一种3层的前馈型神经网络,由输入层、隐含层及输出层组成[28]。图6为本文所采用的RBF神经网络映射关系结构。

图6 高速列车RBF神经网络结构

隐含层节点向量为hi(zi)=[hi1hi2…him]T,其中
(14)
式中:cij为隐含层第i节车厢第j个神经元高斯基函数中心点矢量值,j=1,2,…,13;βij为隐含层第i节车厢第j个神经元高斯基函数的宽度。
(15)
式中:μli为网络的逼近误差,满足|μli|≤μ0。
(16)
2.2.3 RBF神经网络控制器及参数自适应律的设计

(17)

(18)
将式(18)代入式( 8 )可得
(19)
(20)
将理想反馈控制律式( 9 )代入(20),可得
(21)
(22)
式中:参数γ>0;参数χ>0。
3 控制器稳定性分析
设计Lyapunov函数为
(23)
对式(23)求导,并代入式(21),可得


(24)
而由于
(25)
(26)
(27)

(28)
代入自适应律式(22),可得
(29)

(30)

为求解式(30),需用到如下引理[31]。
引理1


(31)
式中:α为任意常数;p为自然常数;f为一个任意的多项式。
根据上述引理,求解不等式(30),对比可得
(32)

(33)
针对式(33)再结合式(32), 又由下式所示的常见不等式
(34)
可得
(35)
由于V(0)有界,则式(35)表明
(36)
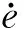
4 仿真与分析
4.1 仿真模型及参数说明
在高速列车模型的建立中,本文选用CRH380B型高速列车的相关参数进行搭建,相关参数见表1,而控制器的相关参数见表2。

表1 列车仿真相关参数

表2 控制器相关参数
同时为验证本文所设计控制方法在高速列车运行于真实线路的控制效果,采用了京石武高铁中北京西—郑州东段的高速列车真实线路运行数据进行仿真模拟。仿真模拟了高速列车在2 h 44 min内的运行过程,运行距离为663.5 km,图7为此段高速铁路线路纵断面示意。由于列车在行进过程中会受到诸如轨面不平、阵风等因素的影响,而这些因素所引起的干扰具有随机性,因此在仿真的过程中,可在列车行驶至236.4~244.84 km时引入一个时变函数fd来表示高速列车在运行过程中所受到的外加干扰,fd=0.012sin(0.015t)+0.024cos(0.033t)。

图7 “北京西—郑州东”区间线路纵断面示意
4.2 仿真结果及分析
为证明本文方法在控制精度,处理复杂路况变化以及抗干扰方面的优势,本文选择与对路况变化和外加干扰具有一定控制效果的反演滑模BSSM方法作为对比对象,载入相同的目标追踪曲线和线路数据,且预设相同的外加干扰,通过仿真可以得到两种方法下高速列车运行过程中各节车厢的位移跟踪曲线和位移跟踪误差曲线见图8和图9。

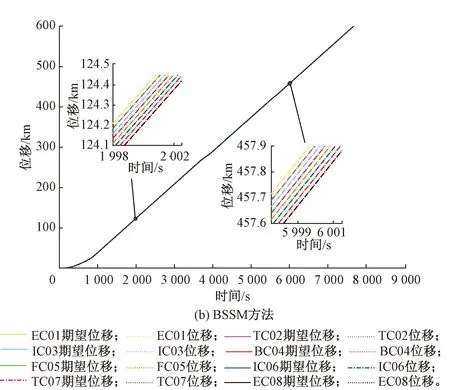
图8 高速列车各节车厢位移跟踪曲线

图9 高速列车各节车厢位移跟踪误差曲线
由图8可见,本文方法及BSSM方法都能实现高速列车对目标位移的跟踪,但由表3的高速列车车厢位移跟踪数据可以看出在相同条件下,本文方法的正负最大位移跟踪误差范围为-0.021 1~0.025 4 m,小于BSSM方法的-0.092 2~0.061 9 m范围;ARBFNN方法下的列车车厢位移跟踪平均绝对误差为0.013 2,相比于BSSM方法的0.059 6更小;并且ARBFNN方法下的列车车厢位移跟踪误差标准差为0.007 7,小于BSSM的0.049 6。说明本文所提出的控制方法具有更高的控制精度。从图9可见,本文方法下的位移跟踪误差波动幅度更小,控制相对更加平稳。

表3 高速列车各节车厢位移跟踪误差统计
通过仿真得到的高速列车各节车厢速度跟踪曲线及速度跟踪误差曲线见图10和图11。

图11 各车厢速度跟踪误差曲线
从图10可见,本文控制方法下的控制效果明显要优于BSSM控制方法。由表4可见,在相同条件下,本文控制方法的正负最大速度跟踪误差范围为-0.188 2~0.348 9 km/h,相比于BSSM方法的-0.938 7~0.801 2 km/h范围更小;本文方法下的车厢速度跟踪平均绝对误差为0.003 9,小于BSSM的0.057 4;并且本文方法下的车厢位移跟踪误差标准差为0.017 6,小于BSSM的0.126 8;说明本文控制方法对列车速度具有更高的控制精度,并且误差波动幅度更小,控制更加平稳,效果很好。对比图11(a)和图11(b),如当高速列车行驶到194.22 km时,列车会行驶进入一个坡道千分数θ为-2的坡道,列车会受到相应的坡道附加阻力,可以看出本文方法下列车行驶至194.60 km时误差趋于了平稳,而BSSM方法下列车行驶至195.10 km时误差才趋于平稳,大幅提升了稳定速度,并且可以看出本文方法下的误差幅度更小。又如当高速列车分别行驶至100、474.89 km时,会分别进入曲线轨道和隧道,会受到额外的曲线附加阻力和隧道附加阻力,同样可以看出本文方法相较于BSSM方法可以以更快的速度实现对目标速度的跟随,且误差的变化量更小,有利于列车的平稳运行,说明了本文方法在处理列车运行路况发生变化时更具优势。当高速列车行驶至236.30 km时,会受到预设的外加干扰,从图11中可以看出本文方法相较于BSSM方法在应对外加干扰时也能够以更快的速度收敛下来,且变化的幅度和次数更少,表明了本文方法具有更好的抗干扰能力。

表4 高速列车速度跟踪误差统计
通过仿真得到的高速列车各节动车车厢控制力变化曲线见图12。对比图12(a)和图12(b)可以看出,如当高速列车行驶至194.22 km时,列车进入坡道会受到额外的坡道附加阻力,可以看出,本文方法下的各动力车厢控制力相较于BSSM方法变化更加的平缓,稳定速度更快;同样当列车行驶分别行驶至100、474.89 km时,会分别进入弯道和隧道,会受到曲线附加阻力和隧道附加阻力,同样可以看出本文方法下的各动力车厢控制力输出相较于BSSM方法稳定速度更快,且相对更平缓,有利于控制器的输出和列车运行的平稳性,表明了本文方法对于处理列车运行路况发生变化时更具优势。而当列车行驶至236.30 km时,列车会受到预设的外加干扰,对比可以看出本文方法相较于BSSM方法的各节动车控制力的输出变化更为平缓且不会出现明显的振荡,说明了本文方法具有更强的抗干扰能力。
仿真得到的两种方法下高速列车各车钩力的变化曲线见图13,对比两种方法的结果图可以看出本文控制方法下的列车车钩力变化相对更加平缓,且车钩力变化范围也相对更小,这对于降低车钩磨损速度,延长车钩工作寿命,提升列车运行平稳性有着重要的作用。

图13 高速列车车钩力变化曲线
5 结论
本文考虑了列车车钩力的作用特点和复杂线路条件,分析整列车前后的不同受力情况,针对高速列车动力分散的特点建立列车纵向动力学模型。在建立的高速列车纵向动力学模型基础上,设计了一种自适应RBFNN控制算法,并且采用了神经网络最小参数自适应学习法,通过设计参数估计自适应律代替神经网络权值的调整,加快神经网络的学习速度,以便于实际工程的应用。仿真结果表明该控制方法相较于BSSM控制方法对于给定的速度和位移具有更高的跟踪精度,且在应对复杂路况及外界未知干扰时具有更好的控制效果,能够改善高速列车运行的平稳性和高效性。
本文的主要贡献是设计了一种具有更高控制精度和处理路况变化以及外界干扰效果更好的高速列车运行控制器,并采用实际线路数据仿真验证了所提方法的有效性,然而由于高速列车运行速度高,运行过程不容出错,目前在实车上进行测试验证还有一些局限,只有先将算例仿真研究全面,方可进入实车验证工作。并且本文在控制器设计时未考虑列车实际运行时不同环境下的轮轨黏着约束对列车运行控制影响,这也是作者需要进一步研究的内容。

