3万t重载列车制动工况纵向力关键影响因素分析

何 闻，常崇义，王俊彪，郭 刚

(1.中国铁道科学研究院 研究生部，北京 100081；2.中国铁道科学研究院集团有限公司 铁道科学技术研究发展中心，北京 100081)

重载运输具有运能大、效率高和经济性好等特点,长期以来都是国内外铁路货运的重点发展方向。我国大秦、朔黄铁路已经常态化开行2万t重载组合列车,但随着我国国民经济的飞速发展,现有的重载线路运能已不能满足日益增长的货物运输需求,为进一步提高运能,最经济的措施便是常态化开行3万t组合列车。但开行3万t组合列车是一个涉及多学科的复杂系统性工程,大秦线首先于2014年3～4月进行了3万t重载组合列车的试验工作,试验中首当其冲的便是与行车安全密切相关的列车纵向动力学问题。3万t组合列车由于编组长度增加,列车所占线路纵断面复杂,加之司机操纵难度的提高,列车纵向力变化更为复杂,操纵不慎便容易导致列车断钩、脱轨事故的发生,因此明确列车纵向力变化规律是开行3万t组合列车的关键一步。目前对纵向动力学的研究手段主要包括线路试验与仿真分析。仿真分析与线路试验相比,人财物成本更低,获得的数据更为全面,且可以进行多种极限工况的分析,并为线路试验验证提供数据参考,因此受到国内外学者的广泛青睐。

文献[1]通过对3类常见钩缓系统进行仿真对比,对其纵向动力学性能和疲劳磨损表现进行了分析说明。文献[2]通过建立列车纵向动力学仿真模型,对2万t组合列车纵向力在不同延迟时间和制动初速下的变化规律进行了研究。文献[3]对ECP制动系统下的列车纵向模型进行模拟仿真,据此研究了重载列车速度调节、车钩力水平、能耗管理等重点关注问题。文献[4-5]通过建立列车空气制动系统与列车纵向动力学联合仿真模型,对3万t组合列车纵向力在不同的从控机车滞后时间下的规律以及循环制动过程进行了研究。文献[6]同样是通过列车空气制动系统与列车纵向动力学联合仿真模型,研究最高减压50 kPa的列尾装置对2万t组合列车的影响。文献[7]基于大秦线3万t综合试验结果,对尾部SS4机车在列车牵引及制动方面的作用进行了分析说明。文献[8]通过建立超长重载列车纵向动力学仿真模型,对4万～12万t重载列车在编组长度、机车无线同步控制延迟时间和长大下坡道的坡度差等因素影响下的纵向力规律进行了分析。

本文通过建立长大重载列车纵向动力学仿真模型并使用制动试验数据验证,计算分析制动工况下3万t组合列车的电控空气制动(electronically controlled pneumatic,ECP)制动系统、同步操控性、变坡点坡度差、车辆轴重等关键因素对3万t组合列车纵向力的影响,明确指出制动工况下ECP制动系统的使用效果,无线同步操控延时边界值、同步操纵故障时的最大可用减压量、变坡点坡度差边界值以及车辆轴重变化对3万t组合列车纵向力的影响,研究结果可为3万t重载列车的常态化开行以及优化操纵提供数据支持。

1 列车纵向动力学仿真模型

列车纵向动力学仿真模型首先以单节机车或车辆为一个分离体,单个分离体在纵向上具有一个自由度,通过对单个分离体的纵向受力分析,见图1。图1中,α为坡度。其纵向动力学方程为

图1 单节机车车辆纵向受力情况

i=0,1,…,n

(1)

式中:mi为第i辆车的质量;ui为第i辆车的位移;FTi为第i辆车的牵引力(仅作用于机车);FDi为第i辆车的再生制动力(仅作用于机车);FBi为第i辆车的空气制动力;Fwi为第i辆车的总运行阻力;Fc(i-1)、Fci分别为第i辆车的前、后车钩力。

通过将列车中的每一个机车车辆单质点模型在纵向上进行串联,见图2,组合为列车纵向动力学多质点仿真模型,列车总自由度为n+1。

图2 列车纵向动力学仿真模型

列车纵向动力学模型中使用MT-2型全钢摩擦缓冲器或HM-1型摩擦胶泥组合式缓冲器,为准确模拟缓冲器的非线性特性,采用文献[2,9]中的数值模型进行模拟。

空气制动系统模型是影响列车动力学计算精度最重要的子模型之一,如果采用精确建模方法,势必会造成参数调整的困难与计算负荷的显著增大,基于专家知识与大量试验数据而建立的空气制动系统非线性解析模型则较好的保证了计算精度与计算量之间的平衡[10]。

建立复杂的非线性纵向动力学模型后,对式( 1 )采用基于Newmark-β的高精度平衡迭代法进行数值求解,该方法较目前多数的数值求解算法具有良好的计算精度[2]。

通过采用上述模型与算法,在文献[10]中对2万t组合列车在紧急制动下的纵向力仿真结果进行了线路试验验证;在文献[8]中对25 t轴重车辆编组的3万t 组合列车在大秦线K288+320处调速制动的结果进行了实车试验对比验证;为进一步准确评估30 t轴重车辆编组模型的准确性,本文根据山西中南部铁路通道(瓦日线)重载综合试验数据[11]对模型进行验证。12 000 t试验编组为HXD2F机车+HXD1F机车+100辆C96(H)货车+HXD1F机车+HXD2F机车,货车全部使用HM-1型摩擦胶泥组合式缓冲器,列车管定压600 kPa,以制动初速80 km/h在平直道线路进行常用全制动与紧急制动停车。

两类工况下制动距离的对比见表1。由表1可知,制动距离的试验结果与仿真结果之间的误差不超过10%;在对应测试断面上的最大压钩力实测值与计算值的对比见图3,该模型的纵向车钩力计算值与实测值十分接近。经过以上多次的实际线路试验数据验证表明,采用上述模型与算法计算长大重载列车纵向动力学问题具有较高的精度。

表1 12 000 t试验列车编组制动距离对比验证

图3 不同制动工况下的最大压钩力分布对比验证

2 纵向力关键影响因素分析

3万t重载列车由于使用的主从控机车数量与位置不同、车辆类型不同、牵引制动控制技术不同,因此存在多种编组形式。本文在基于2万t组合列车常态化运行经验与2014年大秦线3万t组合列车试验[12]的基础上,机车采用HXD1型电力机车和SS4B型电力机车,车辆采用25 t轴重的C80型运煤专用敞车或30 t轴重的KM98型煤炭漏斗车进行编组。主要编组形式见表2,3类编组均使用LOCOTROL分布式动力控制技术,B编组装有ECP制动系统(采用晋中南通道重载综合试验中的ECP制动系统类型)控制全列制动。

表2 编组组成说明

建立3万t重载组合列车仿真模型时,列车管定压为600 kPa,车辆模型中2辆一组使用牵引杆,缓冲器使用MT-2型全钢摩擦缓冲器,车钩间隙取9.5 mm。

2.1 ECP制动系统对纵向力的影响

对使用25 t轴重车辆的A、B编组(牵引总重均约3.2万t,编组长度均约4 km),计算制动初速60 km/h,在平直道进行常用全制动和紧急制动时的压钩力沿车位分布,其中A编组主从控机车同步操控延时为3 s,B编组由于使用ECP制动系统控制全列制动,制动信号传输时间忽略不计,但各车的制动系统响应时间计为0.3 s。图4为常用全制动和紧急制动时最大纵向压钩力沿车位分布情况(负值代表压钩状态,下同)。

图4 A、B编组在常用全制动和紧急制动下的最大压钩力沿车位分布

由图4可知,在平直道常用全制动工况下,使用ECP制动系统的B编组,其最大压钩力与使用LOCOTROL系统的A编组水平相当;但使用ECP制动系统的B编组在紧急制动时,压钩力水平比A编组下降25%～55%,降低效果较为明显。主要原因在于ECP制动系统与LOCOTROL系统相比,其紧急制动与常用全制动时的制动缸升压过程相近且具备更好的全列制动同步性。

2.2 同步操控性对纵向力的影响

3万t重载组合列车采用LOCOTROL装置进行主从控机车的同步操纵控制,LOCOTROL同步性测试试验表明现场空气制动同步作用延时基本在4 s以内,其中2～3 s延时占比(66.67%)最大[12]。在仿真中选择A编组(“1+1+1+1”编组形式)进行计算,此外文献[13]已经表明“V”形变坡是列车制动的最不利线路断面,因此仿真线路选取大秦线重车方向上“V”形变坡最大坡度差区段之一的K240+000～K245+000(坡度差约8‰)区段,见图5。

图5 大秦线K240+000～K245+000线路纵断面示意

计算时以60 km/h制动初速在K244+000处进行常用全制动和紧急制动停车,主/从控机车无线同步操纵延迟时间分别取为3、4、5 s。同时根据TB/T 1335—1996《铁道车辆强度设计及试验鉴定规范》[14],取紧急制动车钩力限值不超过2 250 kN,常用制动下车钩力限值一般不超过1 500 kN[11]。

图6为不同无线同步操纵延迟时间下,采用常用全制动和紧急制动两种制动方式的最大压钩力分布。可以看到当无线同步操控延迟时间达到5 s后,常用全制动和紧急制动停车时最大压钩力均已超限,在4 s延时下两类制动方式的最大压钩力安全裕量仅为6%和5%,因此在保证3万t组合列车常态化安全运行的条件下,无线同步操控延时需控制在3 s以内。

图6 不同延迟时间下两类制动方式的最大压钩力沿车位分布

2万t组合列车现场常态化操纵经验表明,当实际中无线同步操纵延迟超过5 s时,当前机车操纵状态将继续保持5 s,如果从控机车仍未接到操纵指令,则认为此时列车编组出现同步操纵故障。对无线通信故障下的A编组在平直道和图5所示线路分别进行计算,结果见图7和图8。可见在平直道上当空气制动减压量为70 kPa时,安全裕量仅为6%,因此平直道上可使用的制动减压量需,不超过60 kPa;而在大秦线上坡度差8‰的“V”形坡道区段上,只能使用不超过50 kPa的减压量停车才可保证安全。

图7 平直道上最大压钩力沿车位分布

图8 “V”形坡道上最大压钩力沿车位分布

2.3 变坡点坡度差对纵向力的影响

实际线路中,单一变坡点可分为“V”形和“A”形两类,见图9。图9中,下坡坡度为负值,上坡坡度为正值,坡度差为β-α。文献[13]已表明坡度差大小对列车车钩力具有重要影响。本节以使用25 t轴重车辆的A编组(“1+1+1+1”编组形式)为仿真计算对象,计算主从控机车同步操控延时3 s和制动初速60 km/h下,在“V”形和“A”形变坡点上进行常用全制动和紧急制动时车钩力的变化情况。

图9 两类变坡点示意

经过在“V”和“A”形变坡点上不同的初制动位置进行多次仿真,发现列车前1/2长度越过变坡线路的变坡点处开始实施制动时整体车钩力水平最大,因此以该位置为初始制动位置进行纵向力分析。

由于在实际线路中α与β的取值及范围不尽相同,大量仿真计算表明,在常用全制动和紧急制动下“V”形或“A”形变坡区段的坡度差对纵向力影响较大,而在同一坡度差条件下取不同的α与β对车钩力的影响则较小,故将变坡点坡度差作为主要因素考虑。

图10和图11分别为A编组在不同坡度差的“V”形和“A”形坡道上的最大车钩力分布。其中对于“V”形坡道来说,列车制动过程中压钩状态比拉钩状态更为明显,而对于“A”形坡道而言则相反;此外列车在前1/2长度越过两类变坡点处开始制动时,最大车钩力均约出现在列车中部。

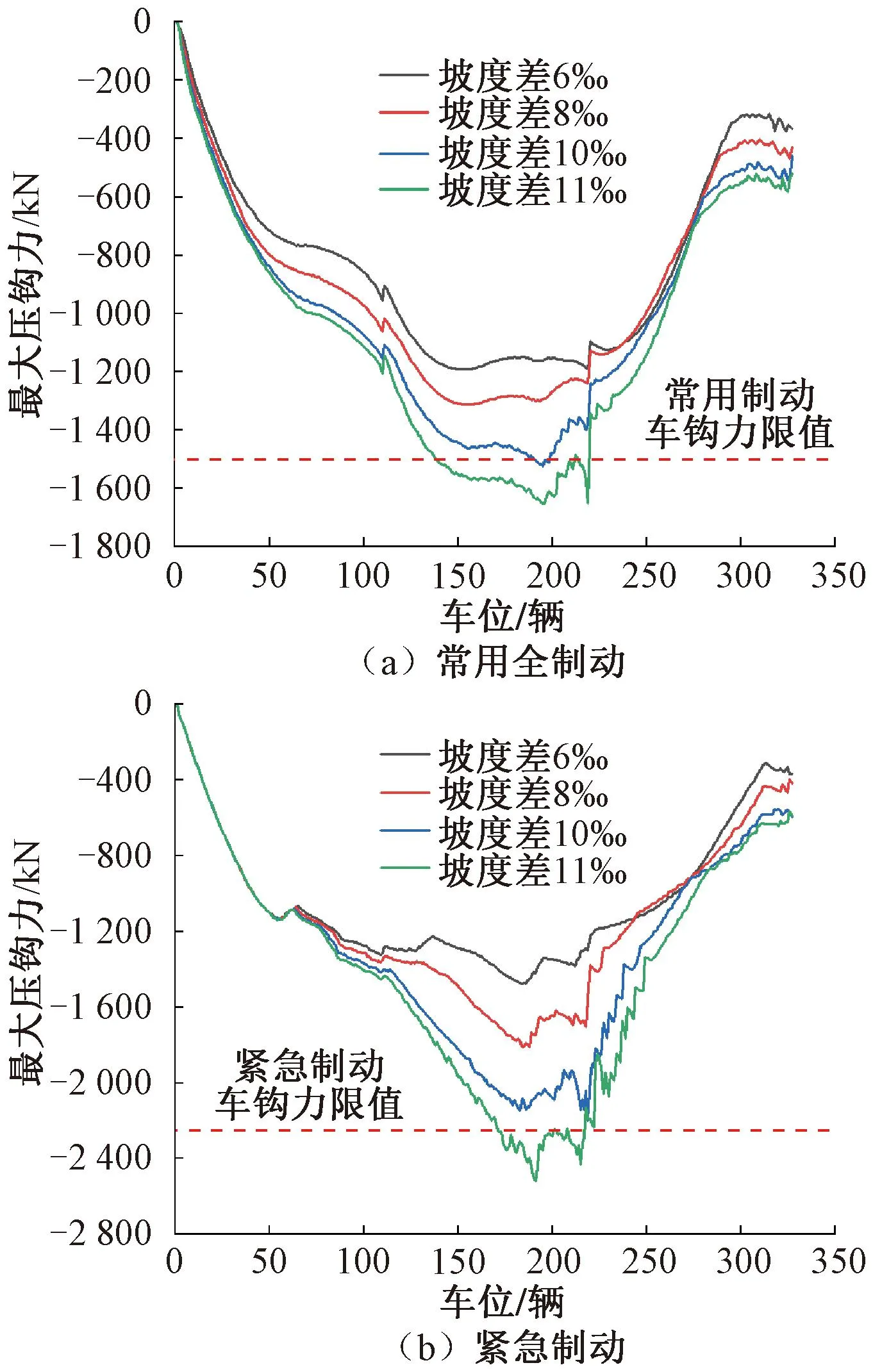
图10 A编组(“1+1+1+1”编组形式)在不同坡度差的“V”形坡道上的最大压钩力分布

图11 A编组(“1+1+1+1”编组形式)在不同坡度差的“A”形坡道上的最大拉钩力分布

对在不同坡度差的“V”形和“A”形坡道上的常用全制动、紧急制动仿真结果进行拟合,见图12。图12中,横轴取正为“V”形变坡,横取负为“A”形变坡。由图12可知,“A”形坡道区段上拉钩力对坡度差变化更敏感,当坡度差大于5‰后最大拉钩力均随着坡度差的增大而线性增长;“V”形坡道区段则对压钩力敏感,当坡度差大于5‰后最大压钩力随坡度差线性增大。此外对于“A”形坡道区段,25 t轴重的3万t“1+1+1+1”编组所允许的最大坡度差为13‰;对于“V”形坡道区段所允许的最大坡度差则为10‰。

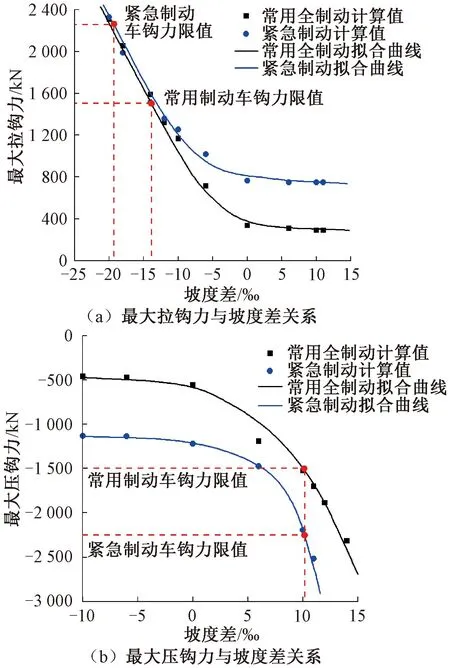
图12 A编组(“1+1+1+1”编组形式)最大车钩力与坡度差的关系

2.4 车辆轴重对纵向力的影响

车辆轴重是货车车辆设计中的重要基础参数之一,实际运营中采用大轴重货车车辆编组可以有效地提高编组运输能力[15]。车辆轴重是货车车辆设计中的重要基础参数之一,实际运营中采用大轴重货车车辆编组可以有效地提高编组运输能力。对使用不同轴重车辆的A、C两类编组进行仿真分析,两类编组均为“1+1+1+1”编组形式,其中A编组使用25 t轴重C80敞车,C编组使用30 t轴重KM98漏斗车,两类编组牵引载重均为3.2万t。对比两类编组在平直道上以初速60 km/h进行常用全制动和紧急制动停车过程中的最大压钩力表现,两类编组的主从控机车无线同步操控延时均为3 s,结果见图13。

图13 不同轴重车辆编组下两类制动方式的最大压钩力沿车位分布

由图13可知,采用30 t轴重车辆编组的C编组与采用25 t轴重车辆编组的A编组相比,在常用全制动和紧急制动下的最大压钩力平均下降约40%。其主要原因:①30 t轴重车辆制动率(重车,常用制动时)为12.3%,比25 t轴重的低3.6%;②30 t轴重编组长度比25 t的略短,约缩短108 m。从纵向动力学表现来看,当线桥隧和装备等条件具备后,大轴重车辆更适合重载运输。

3 结论

1)通过对C96(H)货车编组在平直道上进行列车纵向动力学仿真计算,其计算规律与实车试验结果高度吻合,表明本文重载组合列车纵向动力学模型与数值算法具有良好的精度。

2)组合列车在紧急制动时,使用ECP制动系统比使用3 s无线同步操控延时的LOCOTROL系统压钩力水平可下降25%～55%,但常用全制动下压钩力无明显下降。

3)基于大秦线线路条件,为保证25 t轴重的3万t “1+1+1+1”编组全线常态化安全运行,无线同步操纵延时应控制在3 s以内;若发生无线通信故障,在有较大“V”形变坡坡度差的线路上制动时可用的空气制动减压量不应超过50 kPa,平直道上减压量不超过60 kPa。

4)为保证3 s无线同步操控延时的25 t轴重3万t“1+1+1+1”编组安全运行,“A”形变坡区段允许的最大坡度差为13‰,“V”形变坡区段允许的最大坡度差为10‰。

5)30 t轴重车辆编组的3万t组合列车与25 t轴重车辆编组列车相比,常用全制动和紧急制动下的车钩力平均下降约40%。