寒冷地区海洋环境下高性能混凝土时变特性试验研究

冯 博，朱 海，钱永久

(西南交通大学 土木工程学院，四川 成都 610031)

混凝土的时变性能受多方面因素的综合影响,其定量分析较复杂。目前,针对混凝土时效特性的探索关键主要从两个方面展开:①由材料自身本构关系起始探索混凝土时效周期的表现形式;②从物理试验角度出发,寻找一种实用有效的预测模型[1]。目前尚未找到一种准确分析理论或有效预测模型来准确量化所有类型混凝土的时变特性[2]。由于具有高度不确定性,收缩徐变对结构的后期承载力有极大影响,是混凝土时变最重要的特性,但要精准预估其对桥梁的长期性能影响仍面临巨大的挑战。针对混凝土构件的徐变影响探索,主要通过近似模拟进而逼近真实变化情况进行[3-5]。

目前,我国工程建设中混凝土材料的关键指标以及时变性能主要依据现有规范确定,但规范中混凝土参数取值并未考虑不同自然环境对其的影响。然而,真实的工程结构位于复杂的场地自然环境下,混凝土产品的原始性能、功效演化机制都和标准的理想化预测模型有很大的差异,再加上收缩缓慢变化干扰条件的不确定性,这些都使得混凝土时变特性具有极强的不确定性,实际情况与规范中的预测模型符合程度较差。与此同时,常用的预估模型普遍运用于常规混凝土,测试环境也大部分在较为规范的实验室中,测试条件相对理想,在此环境下获取的试验结果与天然环境下的高性能混凝土的实际性能有一定偏差,结论普适性不高[13-14]。如何让基于标准的预估数值,或者室内试验的实测数值与实际工程场地下桥梁的时效特征较好的符合,一直以来都是研究者们的难题和探索目标。

综上,由于实际场地环境条件和桥梁建设进程互相融合,在桥梁建设过程中展开同位同标准的混凝土时效特征试验研究,是解决以上难题行之有效的方法,获取的成果对桥梁的前期设计与运营期服役养护均有指导作用。鉴于此,本研究采用同位同条件试验对寒冷地区海洋环境下高性能混凝土的时效机能演化机制实施探究,可为该地区同类桥梁结构施工以及运营服役长期收缩徐变控制提供理论支撑和技术指导。

1 混凝土时变特性基本理论

1.1 混凝土抗压强度时变理论

混凝土的抗压强度为其最重要的性能参数,因而对构件的抗压强度进行时效机制探索和预估十分必要。为了简化分析过程,学者们制定了不同的时效演化机制规范,而CEB-FIP规范[15-16]被普遍运用于混凝土性能时效演化的预测。CEB-FIP—2010[16]对混凝土的抗压强度进行了修正,即

fcm(t)=βcc(t)fcm,28

(1)

(2)

式中:fcm(t)为龄期t时为混凝土平均抗压强度;fcm,28为龄期为28 d时混凝土的平均抗压强度;t为混凝土的龄期;βcc(t)为与龄期相关的系数;s为水泥种类的相关系数,在CEB-FIP—1990[15]中取0.25,CEB-FIP—2010[16]中取0.20。

区分于常见混凝土,由于高性能混凝土中掺合料和添加剂的干扰,应基于真实场地环境条件对s的取值进行修正。修正后的HPC抗压强度计算式[16]为

(3)

1.2 混凝土弹性模量时变理论

弹性模量作为混凝土材料的另外一个重要参数,通常受服役环境和时间的影响,呈现较为显著的时变特性,考虑CEB-FIP—2010规范[16]要求,对混凝土的弹性模量随时间的变化进行预测,即

Eci(t)=[βcc(t)]0.5·Eci,28

(4)

式中:Eci(t)为龄期为t时的弹性模量;Eci,28为混凝土龄期为28 d时的弹性模量。

1.3 混凝土收缩特性时变理论

在实际工程案例中,不一样的构件位于相同的服役场景中,能够把环境因素作为控制变量,主要区别为构件大小对其收缩特征的影响,所以精准地预估模型应该可以与不同尺寸构件的收敛进度保持高度的统一性。同样基于CEB-FIP—2010[16]的要求,考虑构件尺寸效应,预测模型的相关参数计算式为

(5)

式中:βds为参考收敛的抗压强度伴随时间进展系数;h为混凝土试件理论厚度,h=2A/u,A为构件的横截面面积,u为截面周长,ts为混凝土干燥开始时的龄期。

2 试验设计

混凝土的时效特性发展规律受多因素干扰影响,为便于分析,试验中通常采用单一变量依次探究方法,经过控制其他变量来探究单一变量的时变特性。因场地条件、混凝土自身参数普遍存在较高的随机性,且其对混凝土时效本质的干扰明显,常见理想状态下的室内测验很难精确复现桥梁桥位的真实场地因素。本文利用同位同参数维护部件的专业“同位维护”,通过控制变量保证测试的构件与实际桥梁构件位于相同的外部环境中,降低外部偏差。

2.1 试验材料

试验研究对象为纳潮河2#大桥,该桥位于唐山市曹妃甸工业区,此地域桥梁的场地环境温度受季节干扰较大,长期以来年平均气温低于13 ℃,最高气温达39 ℃,极限最低气温为-20 ℃,昼夜温差大,而且该地区的相对湿度稳定在66%左右,是较为典型的寒冷海洋环境。试验试件的混凝土用料配合比设计及参数指标见表1、表2。

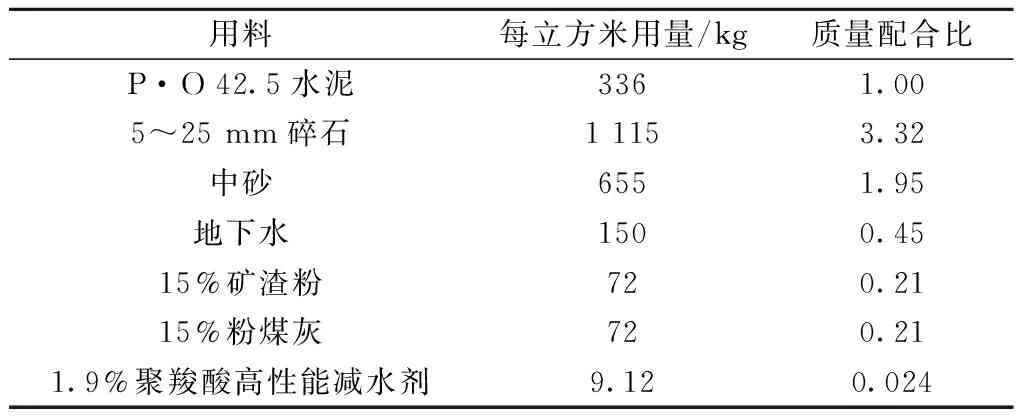
表1 高性能混凝土配合设计

表2 高性能混凝土参数指标

2.2 试验方案

试验同步采用桥梁施工中所用的高性能混凝土,试件与桥梁段施工混凝土同期浇筑,并将其放置于桥梁施工段附近专门的同位养护试验场,与桥梁构件同时养护。本区多年平均气温12.5 ℃,最高气温32.9 ℃,最低气温-14.8 ℃。该地区多年平均降雨量764.2 mm,年最大降雨量1 219.6 mm,年最小降雨量412.0 mm。当高性能混凝土达到要求的凝期后,对选取的构件开展抗压强度、弹性模量、收缩以及徐变试验研究。

1)强度试件

制作6组强度实验试件,每组6个标准试件,混凝土标号为C50,试件与大桥主跨T构同时施工浇筑。各组试件的试压龄期见表3。按照GB 50010—2010《混凝土结构设计规范》[14],选取尺寸为150 mm×150 mm×150 mm的标准混凝土立方试件进行抗压测试。

表3 强度试件分组

2)弹性模量试件

弹性模量测试部件同样为6组,每组6个标准试件,仍选用C50混凝土,构件大小采用抗压弹性模量标准部件尺寸。试件在试压测试时的养护龄期如表4所示。

表4 弹性模量试件分组情况

3)收缩试件

收缩试件分为两种尺寸:100 mm×100 mm×515 mm、300 mm×300 mm×2 500 mm,每种6个。由于纵筋与横筋交叉布置会对混凝土收缩产生约束作用,该部分均采用素混凝土试件,不内置钢筋。为精确获取应变值,应变传感器安装于试件内部并整体浇筑。分段对试件进行测量:第一阶段测试开始于拆模后,随后每天一次,直到龄期满足28 d;然后开始第二阶段,每两天进行测试,直到龄期满足60 d;最后为第三阶段,每周进行一次测试,直至试验结束。

4)徐变试件

徐变混凝土试件浇筑9个,每个试件内配置4根直径10 mm的纵筋,并选用直径6 mm的箍筋间距300 mm布置。试件尺寸为300 mm×300 mm×3 500 mm。预应力的钢束选用单束7φ15.2。振弦式传感器整体浇筑于试件内部两侧。混凝土龄期满足3、5、28 d时对每组试件进行张力测试。检测周期为:拆模检测一次,随后每天固定检测一次,直到张力施加环节;在张力测试阶段实验前后各进行一次检测,实验后每天都进行检测直到28 d龄期;然后每2 天进行一次测试,直到满足60 d龄期;最后每周检测一次,一直到测试完结,徐变试件尺寸大小见图1,本研究中徐变试件应力水平为0.35 MPa。

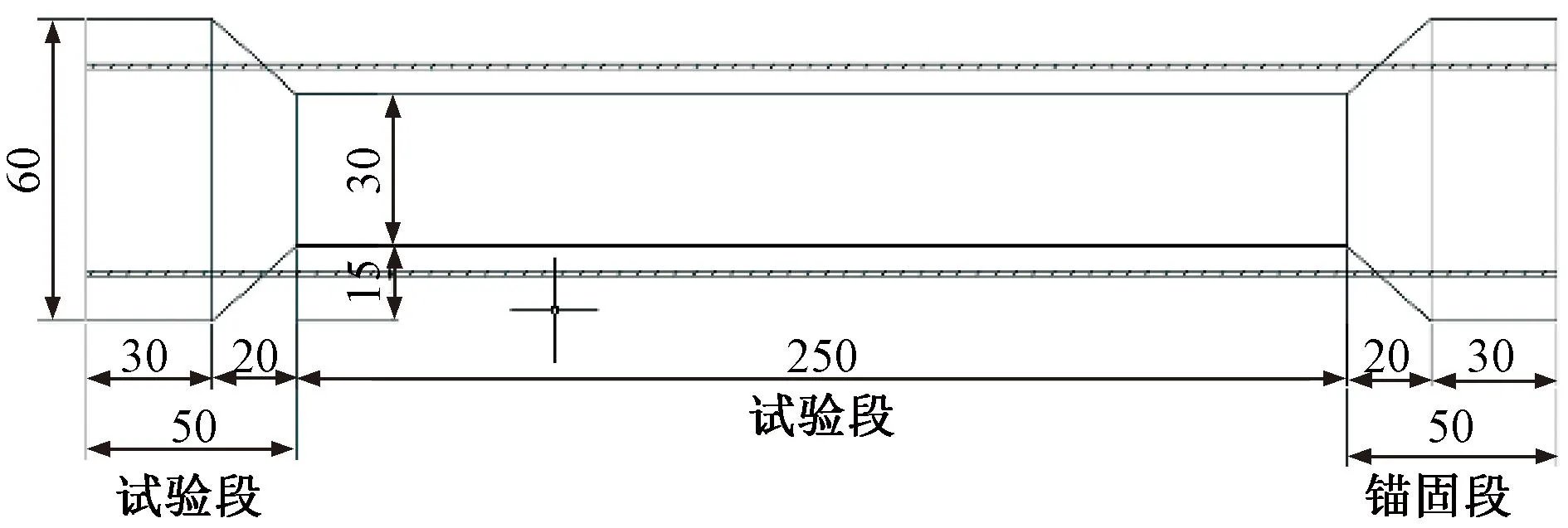
图1 徐变试件尺寸(单位:cm)

3 试验结果及分析

3.1 抗压强度

经过抗压强度试验结果见表5,由表5可知,6组混凝土构件的立方体抗压强度平均值。对于ST3试件,其抗压强度测试的平均值为45.93 MPa,满足GB 50010—2010《混凝土结构设计规范》[14]中对混凝土试件强度所要求数值;对于ST28试件,其抗压强度平均值为70.60 MPa,远高于规范中所要求的标准值,因此满足C50的设计等级要求。

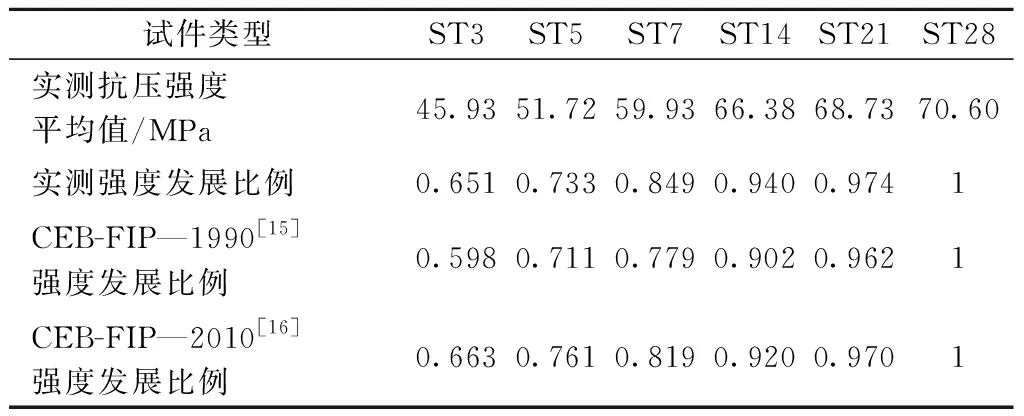
表5 抗压强度实测平均值及发展比例

为了对比分析本文寒冷环境高性能混凝土抗压强度试验值与常温环境实验值的异同,本文通过广泛查阅文献资料,依据试验工况设置条件,给出文献[17]的试验值作为对照,具体对比分析见表6。

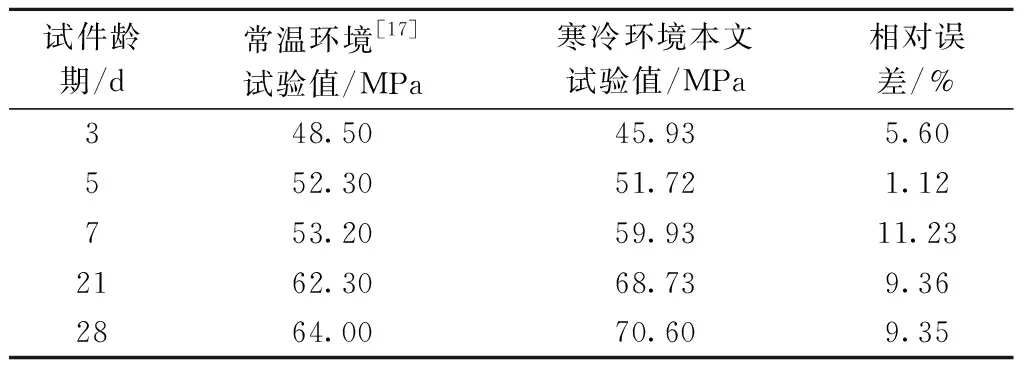
表6 寒冷与常温环境高性能混凝土抗压强度试验对比

从表6中结果来看,试件龄期分别为3、5 d时,寒冷环境高性能混凝土抗压强度本文试验值小于常温环境文献[17]试验值,说明常温环境下高性能混凝土初凝更为迅速,但之后随着试件龄期的增大,寒冷环境下混凝土抗压强度逐渐大于常温环境,这可能是由于随着龄期的增加,温度效应作用逐渐减弱,最终强度与混凝土试件添加剂及其配合比有关。但两者总体偏差较小,基本在10%以内。

试件实测抗压强度及基于CEB-FIP—1990[15]和CEB-FIP—2010[16]的预测抗压强度时变特征值见图2。

图2 抗压强度时变特性曲线

从图2可以看出:高性能混凝土抗压强度在初期(7 d内)进展迅猛,随着龄期延长(7 d后)而放缓。虽然从第14 天起,实测强度和预估值吻合程度很高,然而在3、5、7 d时的实测值都远超出预估值。以上结果与混凝土所取用的掺合料品质、减水剂的添加、外部场地温度,以及维护养护手段都有很大关系。分别将CEB-FIP—1990[15]和CEB-FIP—2010[16]的抗压强度预测值与试验实测值对比可以看出,CEB-FIP—2010[16]的预测结果在初期明显优于CEB-FIP—1990[15],随着时间的推移,两个按照标准设计的混凝土抗压强度估计量逐渐接近实际指标。整体对比结果表明,采取现存规范机制预估高性能混凝土抗压强度时变趋势时,会低估其初期(7 d前)抗压强度。

CEB-FIP—1990[15]和CEB-FIP—2010[16]中水泥影响因子s分别取0.25和0.20,对高性能混凝土时变性能而言,s是对抗压强度十分关键的影响因素,且该参数与混凝土掺合料和添加剂有着密切的联系。针对本桥的高性能混凝土,需把实测部件作为标尺,通过不同周期实测抗压强度数据实施解析回归,进行参数s修订。修订后的s取0.16,得抗压强度时变表达式为

(6)

根据式( 6 )得到抗压强度预测趋势曲线的修订结果,其与抗压强度实测值的对比见图3。从图3可以看出,当s=0.16时,预测曲线与实测值吻合得很好,表明针对本桥高性能混凝土的特点,采用修正后的抗压强度解析表达式能够很好地预测高性能混凝土抗压强度时变规律。

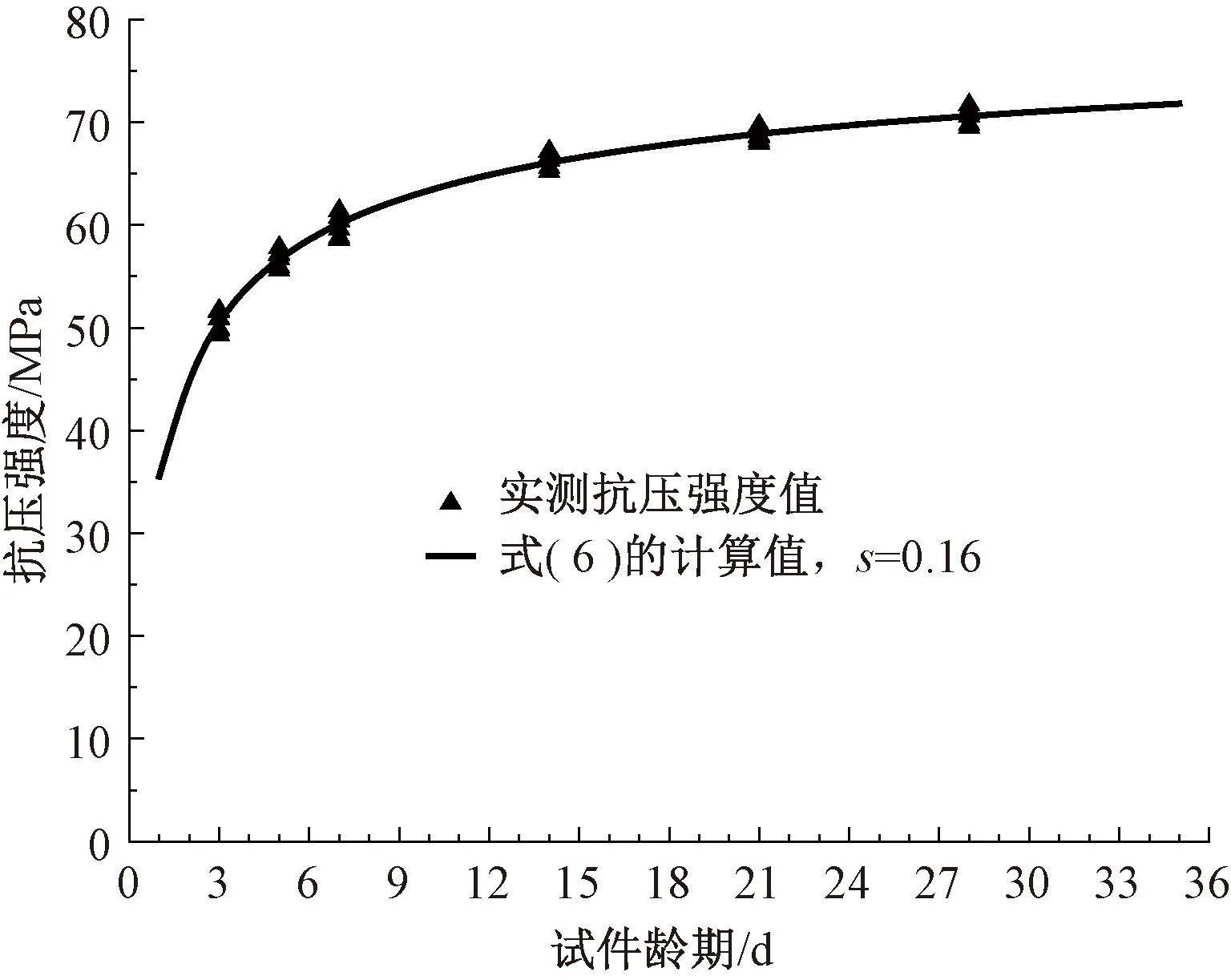
图3 修正后的强度曲线

3.2 弹性模量

弹性模量试验结果见表7,其给出了6组不同测试龄期混凝土弹性模量试验结果的平均值。由表7可知,当试件龄期为3 d时,其实测弹性模量平均值为32.33 GPa,略低于文献[14]中的标准值34.5 GPa;逐步增加混凝土测试龄期,其弹性模量实测值与龄期呈线性关系;当测试龄期达到28 d时,实测弹性模量平均值达到了48.45 GPa,远大于文献[14]中的标准值。

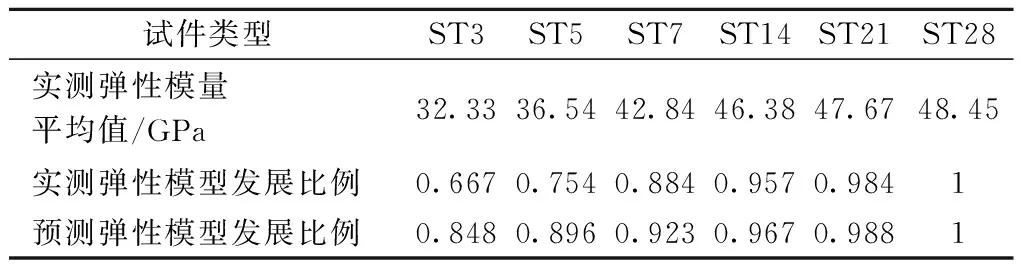
表7 试件弹性模量平均值及发展比例

同样地,为了对比分析寒冷环境下高性能混凝土弹性模量试验值与常温环境弹性模量的异同,仍以文献[17]的试验值作为对照,给出了两种试验条件下的试验值,具体试验结果对比分析见表8。

表8 寒冷与常温环境高性能混凝土弹性模量试验对比

从表7中可看出,其与高性能混凝土抗压强度规律一致,当试件龄期分别为3、5 d时,寒冷环境下的弹性模量试验值小于常温环境[17]的试验值,同样由于常温环境下混凝土初凝更为迅速,此后,随着龄期增加,寒冷环境下混凝土弹性模量试验值逐渐大于常温环境[17]混凝土弹性模量试验值。

表9为3种标准规范关于高性能混凝土弹性模型的预测值,并将该预测值和实测值进行比较分析。从表9中可以看出,JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》[13]、CEB-FIP—2010[16]以及EN 1992-2—2005[18]规定的C50混凝土弹性模量分别为34.5、36.3、35.0 GPa,如考虑时变特性,28 d龄期按照3种规范推算得到的弹性模量预测值分别为37.01、39.79、38.28 GPa。如若出现添加引气剂,或者较高砂率的泵送混凝土且无实测数据的情况,3种规范均采用乘以0.95的折减系数应对。28 d龄期的高性能混凝土弹性模量实测平均值为48.45 GPa,由此得出:采用3种规范推算得到的28 d龄期混凝土弹性模量虽远大于规范规定值,但仍小于实测数据,这表明既有标准对于高性能混凝土的能力预估存在一定的不足,亟待改进。

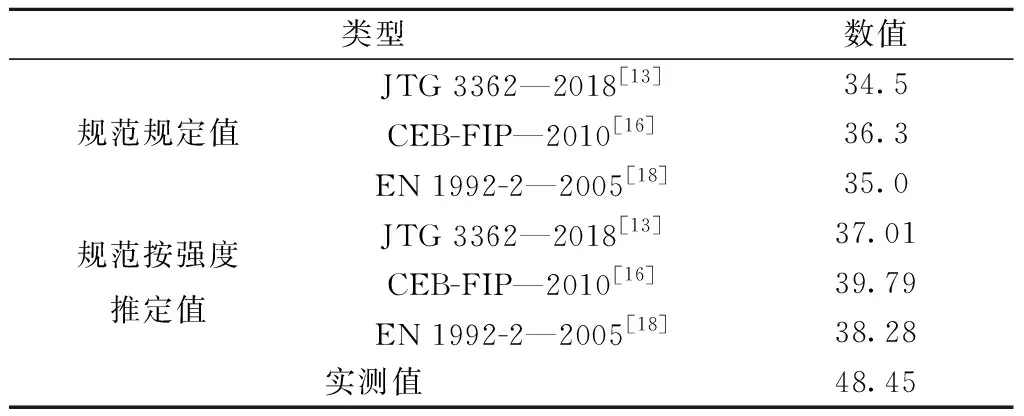
表9 规范推算弹性模量与实测值对比结果 GPa

根据表7的混凝土试件弹性模量试验结果,参照式( 3 ),同样取s=0.16,则高性能混凝土弹性模量随龄期发展的实测值,以及根据文献[16]得得到的预测值见图4。从图4中可以得出,当混凝土试件龄期低于9 d时,混凝土弹性模量预测值大于实测值,随着时间的持续变化,预测值与实际值基本吻合。

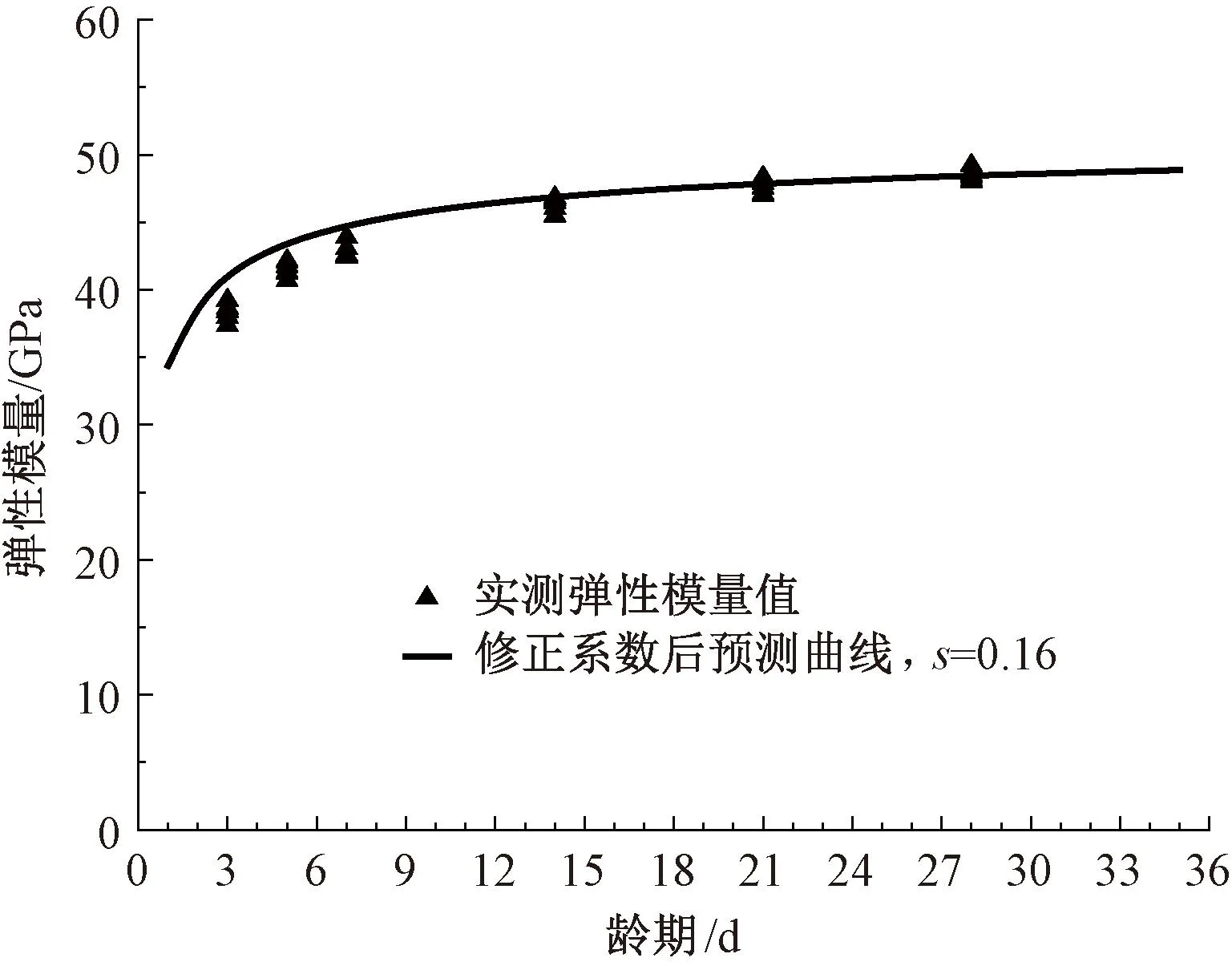
图4 弹性模量曲线

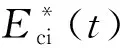
(7)

修正后弹性模量预测曲线与实测值的对比见图5。由图5可知,修正后的弹性模量预测曲线与各龄期测试值能够很好吻合,表明早期弹性模量发展滞后的不足可以通过式( 7 )进行修正弥补。

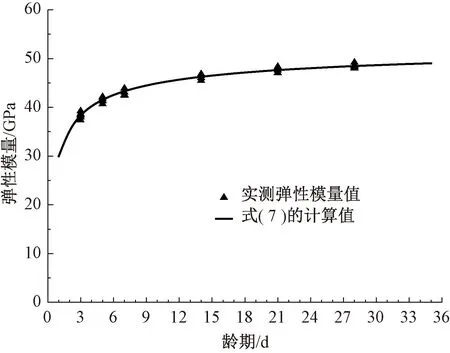
图5 弹性模量修正曲线

3.3 收缩特性

实际工程中,工作环境对不同结构构件材料参数影响不大,但不同尺寸引起的尺度效应会导致实际结果与预测模型有显著差异。由此可见,有效的混凝土收缩预测模型理应能够与不同尺寸部位构件的收缩变化保持较高的一致性。本试验重点研究截面边长a取100、300 mm时试件收缩应变实测值随龄期发展规律,两者的收缩对比见图6。从图6中可以得出,a=100 mm时试件收缩应变明显大于a=300 mm时,收缩应变受构件尺度效应影响显著。

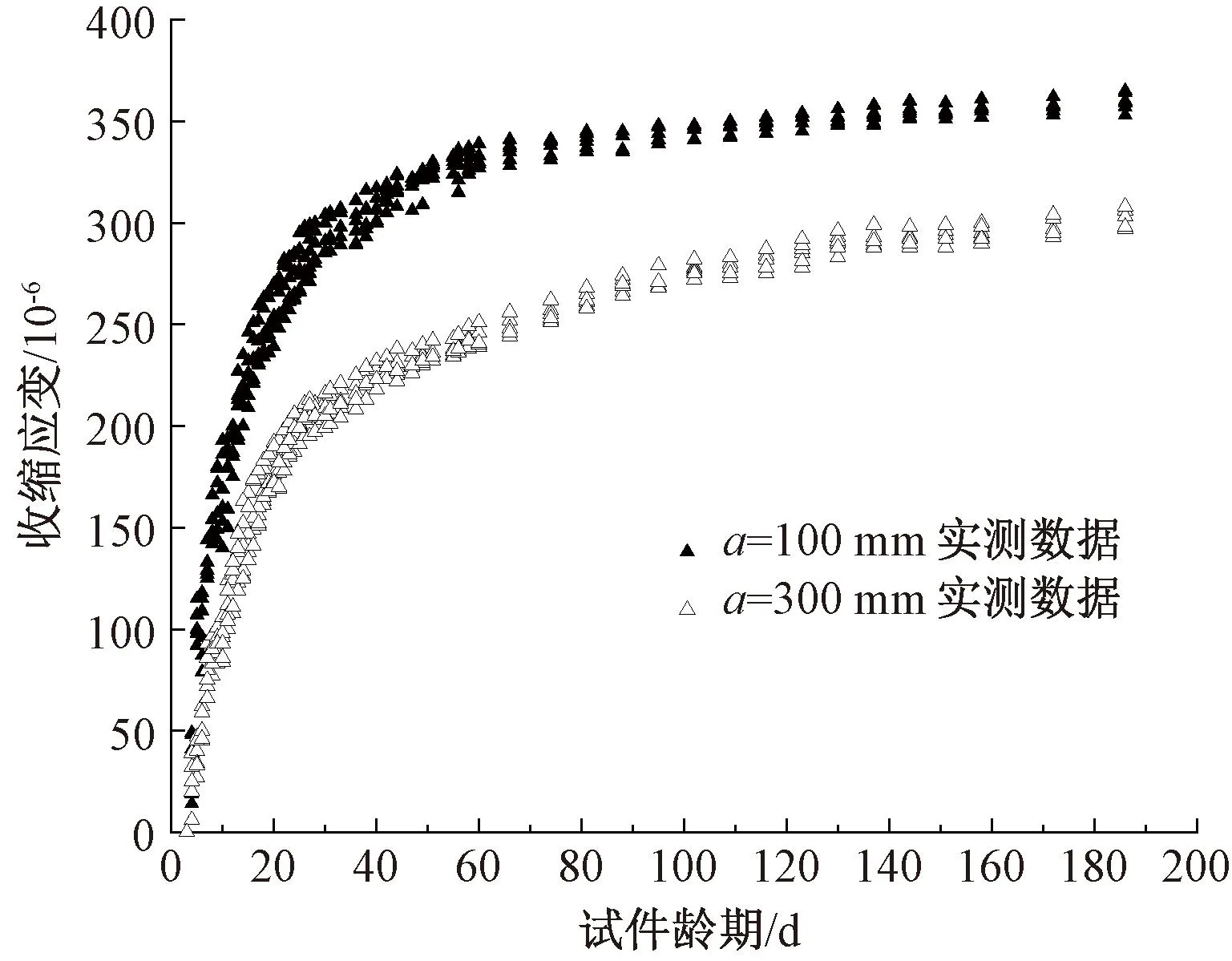
图6 不同构件收缩曲线

图6还反应了两种尺寸试件的收缩应变发展趋势,两者都呈现出30 d前快速增长,30 d后发展减缓的趋势。与常用的混凝土有所不同,虽然高性能混凝土前10 d龄期收缩发展趋势迅猛,但收缩应变的收敛区域也出现得相对较早。小尺寸的混凝土构件拥有更短的收缩前期,且收缩终值较大,但其收缩的发展收敛区域更为狭小,这一现象的形成是因为尺寸小的混凝土构件拥有更大的暴露于环境的外表面,这使得混凝土内部水分迅速挥发,较早收缩以致收敛。

同样地,为了对比分析寒冷条件及常温条件下高性能混凝土收缩应变的差异,依据试验条件参数,取a=100 mm,并考虑高性能混凝土配合比等试验参数的匹配性,选用文献[19]中常温环境下编号C3的试验组作为对照进行对比分析,见图7。

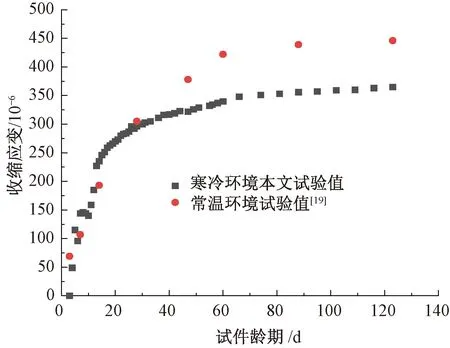
图7 寒冷环境与常温环境高性能混凝土收缩应变实测值对比(a=100 mm)

从图7可以看出,常温环境下收缩应变试验值在整个龄期内均大于寒冷环境下的试验值,且随着试件龄期增大,二者差距进一步增大,但总体来看当试件龄期大于120 d以后,两种试验收缩应变均趋于稳定。从对比结果可知,温度对高性能混凝土收缩应变试验值的影响较为显著,寒冷环境能够抑制高性能混凝土收缩应变的发展。

由于现有收缩徐变预测模型都属于半经验模型,所考虑的影响因素不尽相同。作为对比,本文选择CEB-FIP—1990[15]、2010[16]、欧洲标准EN 1992-2—2005[18],以及GL 2000[20]模型和实测值进行比较,对所选的4类模型的适用性进行研究,模型考虑的各影响因素如表10所示,分析结果见图8和图9。

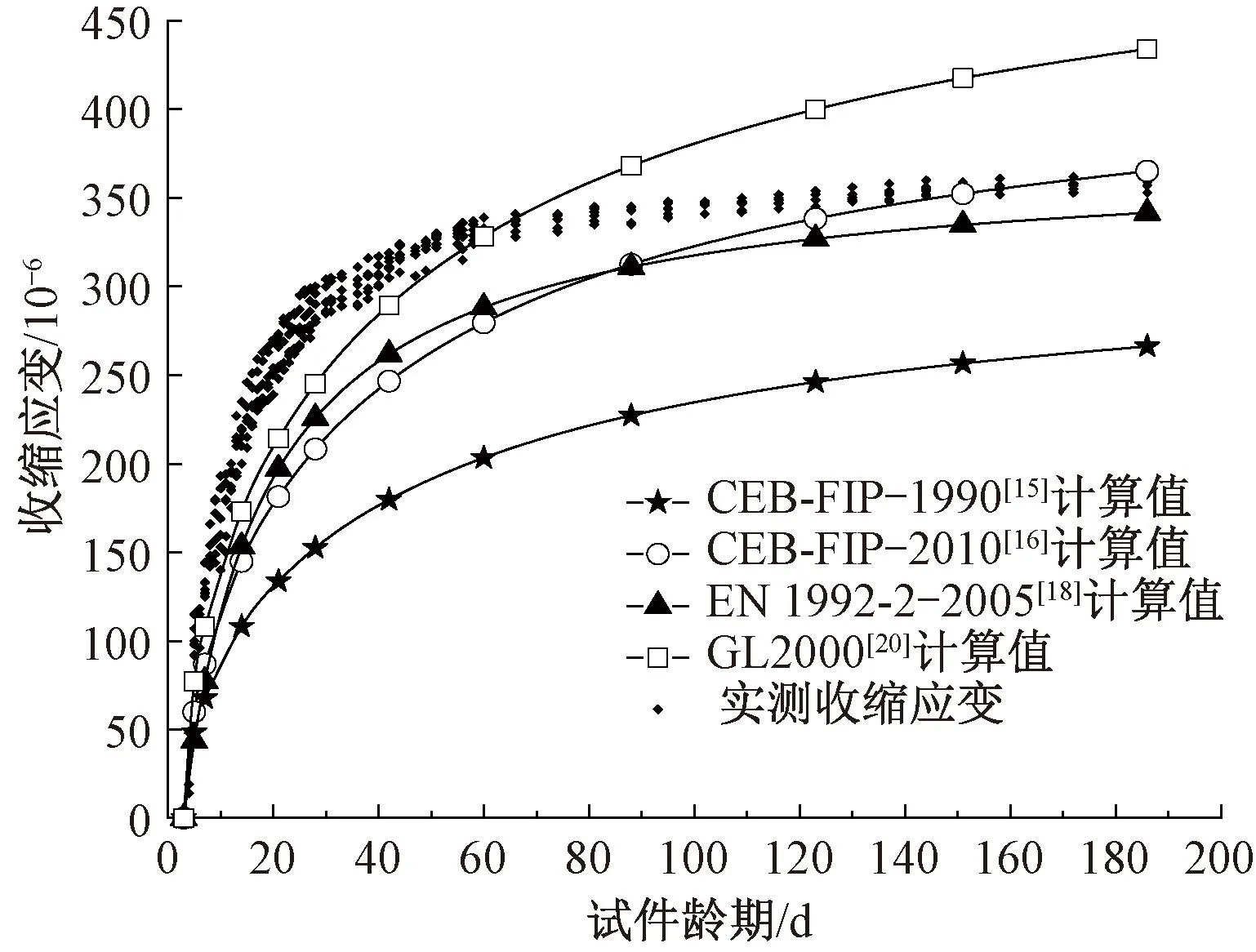
图8 实测值与不同预测模式对比(a=100 mm)

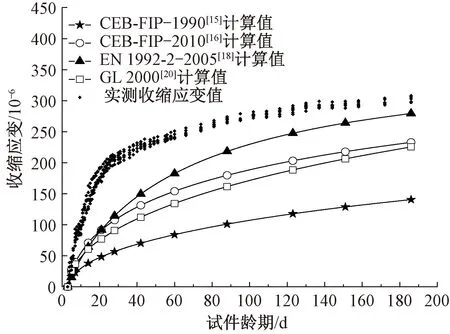
图9 实测值与不同预测模式对比(a=300 mm)

表10 预测模型考虑的影响因素

由图8和图9可以分析得到:CEB-FIP—1990[15]标准模型的收缩应变在各龄期均为最小,整体收缩区间预测值偏小。按照规范[14]要求,我国桥梁设计选用该计算模型,这会导致对混凝土徐变收缩的预测不足。从早期的收缩发展趋势来看,几类模型的短龄期内的应变值均低于实测值,低估了收缩发展趋势;当试件边长a=100 mm时,CEB-FIP—2010[16]以及GL 2000[20]模型于160 d龄期时超越了实测值,高估了收缩的后期发展;4类预测模型对于不同尺寸试件收缩的预估值具有一定差距,这是由于各预测模型均高估了小尺寸构件全龄期内的徐变收缩而低估了大尺寸构件的收缩变化导致的。高性能混凝土具有早期收缩迅速且收敛区间窄的特性,直接使用上述几种预测模型对高性能混凝土进行收缩预估可能产生较大的偏差。

鉴于以上研究,若不对上述几种预测模型进行一定修正,其对高性能混凝土的收缩预测将难以满足相关要求。为此,依托对纳潮河2#大桥的实测数据,以CEB-FIP—2010[16]预测模型为基础,对影响混凝土徐变收缩的相关时间参数以及构件尺寸参数进行修正,得出适用于本试验高性能混凝土收缩发展的预测模型。修正后的预测公式为

(8)

(9)

(10)

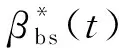
从收缩试验值与规范的预测值比较可以看出,在试验时间段内收缩的发展过程试验值和规范预测值都存在明显差异。所以选用CEB-FIP—2010[16]收缩模型进行参数拟合修正时,需要考虑收缩随时间的发展系数。

修正后的预测情况如图10所示。

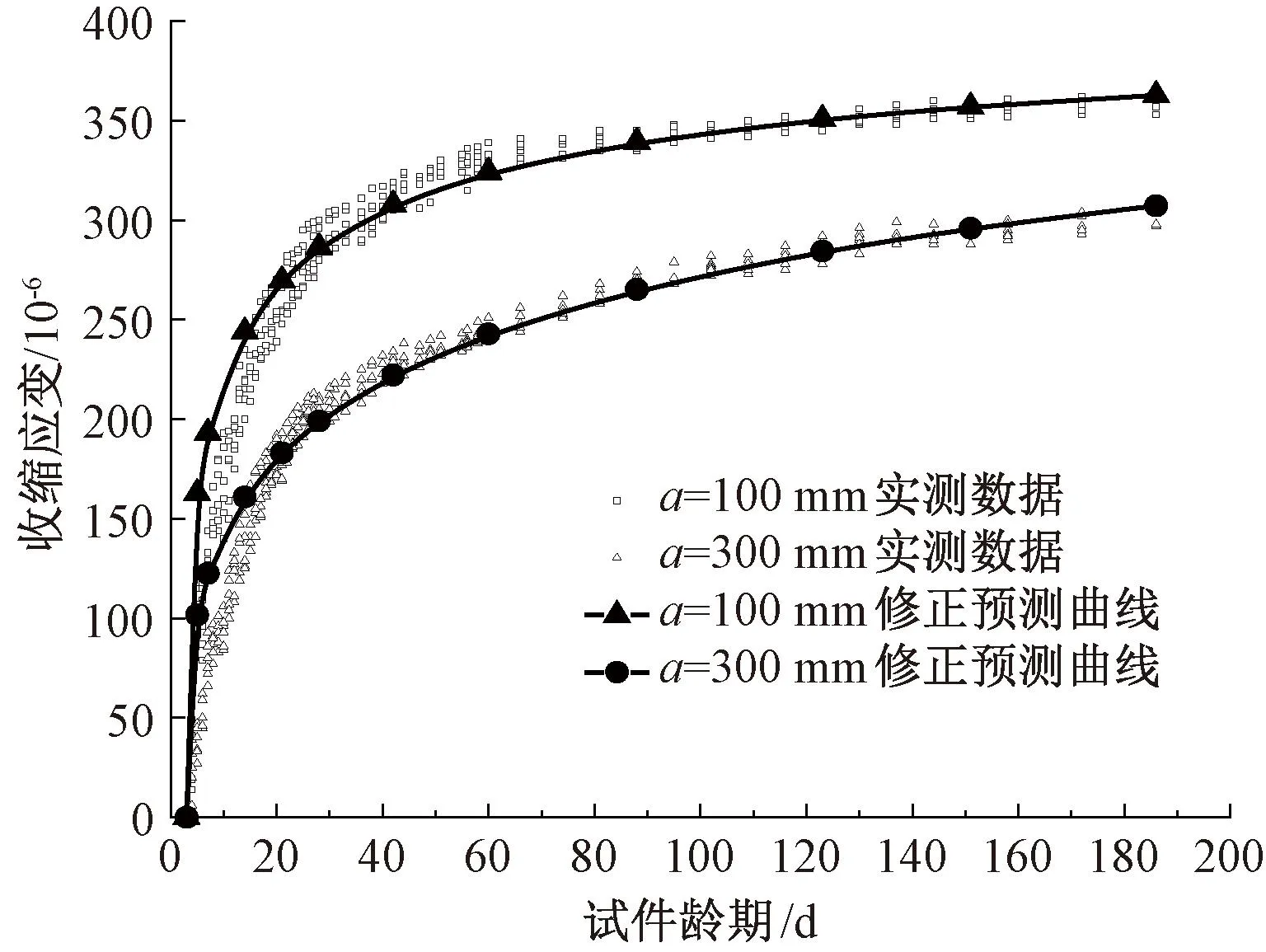
图10 实际收缩应变与修正预测模型比较

混凝土收缩主要表现为水泥硬化过程的体积收缩,其中水泥的矿物成分主要为硅酸三钙(3CaO·SiO2),其与水相遇时能够迅速抓住水分子螯合为结晶水,然后晶体不断发展,形成强度,放出热量的同时体积收缩。

就修正的结果而言,整体效果良好,然而要符合各种尺寸部件仍有困难。从图10可以看出:当龄期不足20 d时,修正后的预测应变大于实测值;当龄期大于20 d时,修正的预测模型对收缩变化后期的发展预估可能偏大。从整体来看,修正后的预测模型对HPC全龄期的收缩预测是有效的。

3.4 徐变特性

对于具有不同龄期、应力的双变量影响的混凝土徐变应变对比试验是难以直接获得明显变化规律的,因此各国均通过选用不同的徐变影响系数对徐变发展规律展开研究[23-24]。根据加载时构件的弹性模量以及不同加载时间节点,本试验选取相应的徐变系数进行分析计算,图11给出各载荷龄期的徐变系数发展趋势。

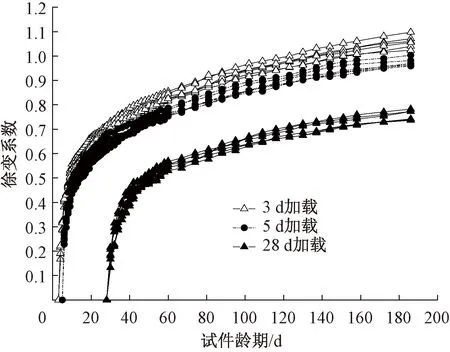
图11 各载荷龄期的徐变系数发展趋势

由图11可以看出:对于不同的加载时间,徐变系数在发展初期都变化较快。随着时间进程的增加(10 d龄期后),变化趋势逐步放缓。试件于28 d加载得到的徐变系数的龄期收敛区间较短,3 d加载的龄期收敛区间较长。当加载时的龄期节点相同时,构件的加载应力变化对于徐变系数影响较小。

为对比分析寒冷条件以及常温条件下高性能混凝土徐变系数的差异,依据试验条件参数,选取加载时间为5 d的工况,并考虑高性能混凝土配合比等试验参数的一致性,选用文献[25]的中编号3#的试验组作为对照,然后将本文寒冷环境下收缩应变与常温环境下的徐变系数试验结果进行对比分析,如图12所示。

图12 寒冷与常温环境徐变系数试验值对比(5 d加载)

从图12中可以看出,常温环境下高性能混凝土徐变系数试验值[25]在整个龄期内均大于寒冷环境试验值,当试件龄期大于180 d以后,两种试验应变值均趋于稳定。同样从对比结果可知,温度对高性能混凝土收缩应变试验值的影响同样较为显著,寒冷环境能够减缓和抑制高性能混凝土徐变系数的发展。

本文选用了CEB-FIP[15-16]系列、EN1992-2[18]、GL 2000[20]、 ACI 209R[21]以及AASHTO[22]模型和实测徐变系数进行对比分析,见图13。

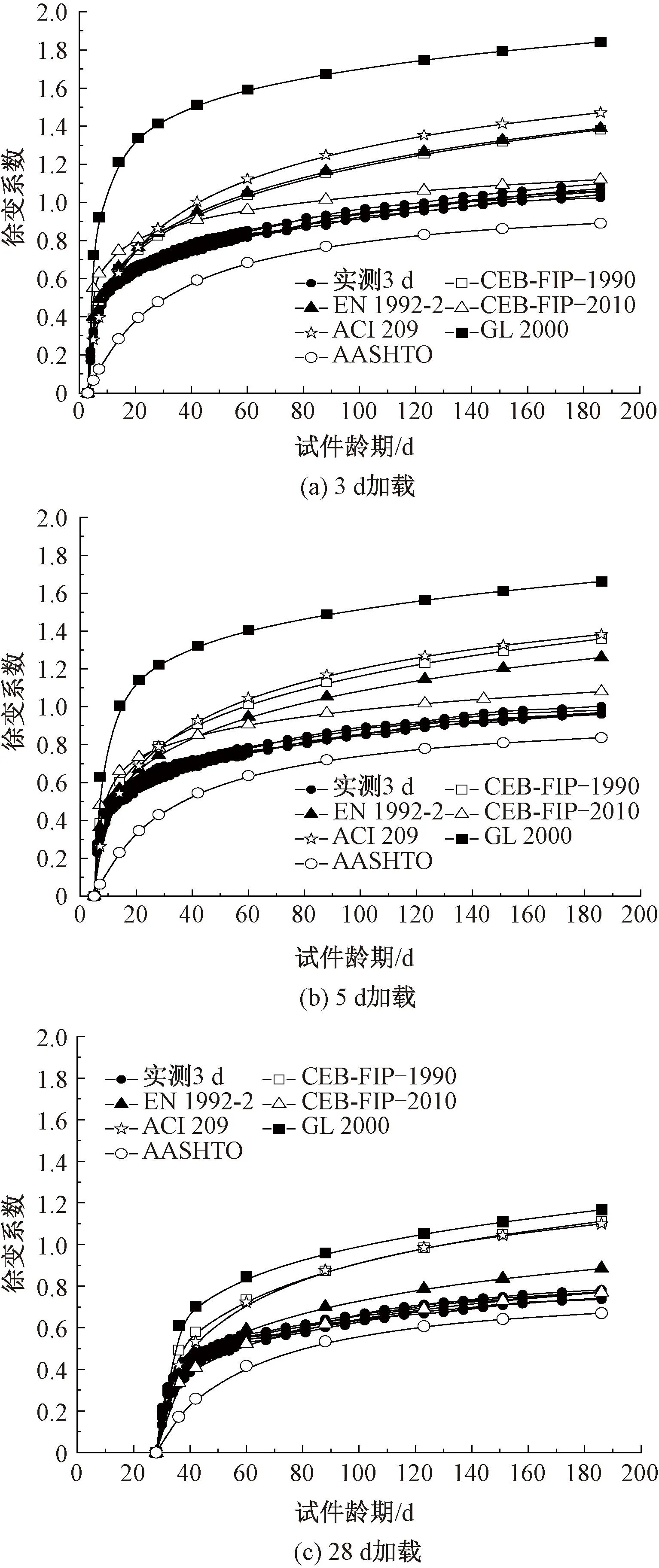
图13 徐变系数与各模型对比

由图13可以看出:各模型预测的徐变系数发展趋势与试验得到的实测值吻合较好。当龄期小于10 d时,徐变系数处于迅速上升阶段;当龄期大于10 d时,徐变系数发展逐渐放缓。从加载的时间节点来看,加载的时间越早对徐变的影响越大。从图13中还可以明显的得到:GL 2000预测模型的计算结果于各龄期都明显偏高,且ACI 209、CEB-FIP系列以及欧洲规范EN 1992-2均大于本试验的实测值,AASHTO模型的预测结果明显偏小。

当加载龄期为28 d时,CEB-FIP—2010模型与本实验实测值有较高的拟合程度,但当加载龄期为3 d或5 d时,该模型的徐变系数均高于实测值。对于预测模型本身而言,结果总体呈现GL 2000>ACI 209>CEB-F2P—1990>EN 1992-2>CEB-FIP—2010>AASHTO的关系。从上述结论中可以看出,CEB-F2P—1990模型对于加载龄期敏感度较高,其早龄期加载时与EN 1992-2模型一致,而晚龄期加载时与ACI 209模型一致。

考虑各个预测模型在实际设计案例中的运用程度,本文选用了与实测值吻合程度较高的EN 1992-2预测模型,即GB 50010—2010《混凝土结构设计规范》[14]对于混凝土结构所采用的预测模型进行修正,即

(11)

(12)

(13)

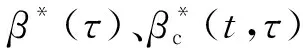
从试验数据与预测模型对比可以发现,徐变偏差与28 d强度有一定的相关性,且不同试验段偏差也不同,表明偏差还与理论厚度及加载应力比有关。影响徐变的因素多而复杂,鉴于本次试验获得的数据与完全修正一种预测模型尚有差距,本次修正仅考虑了混凝土强度和加载龄期对名义徐变的影响,以及加载龄期对徐变随时间发展系数的影响。

修正后的预测模型与实测值比较如图14所示。

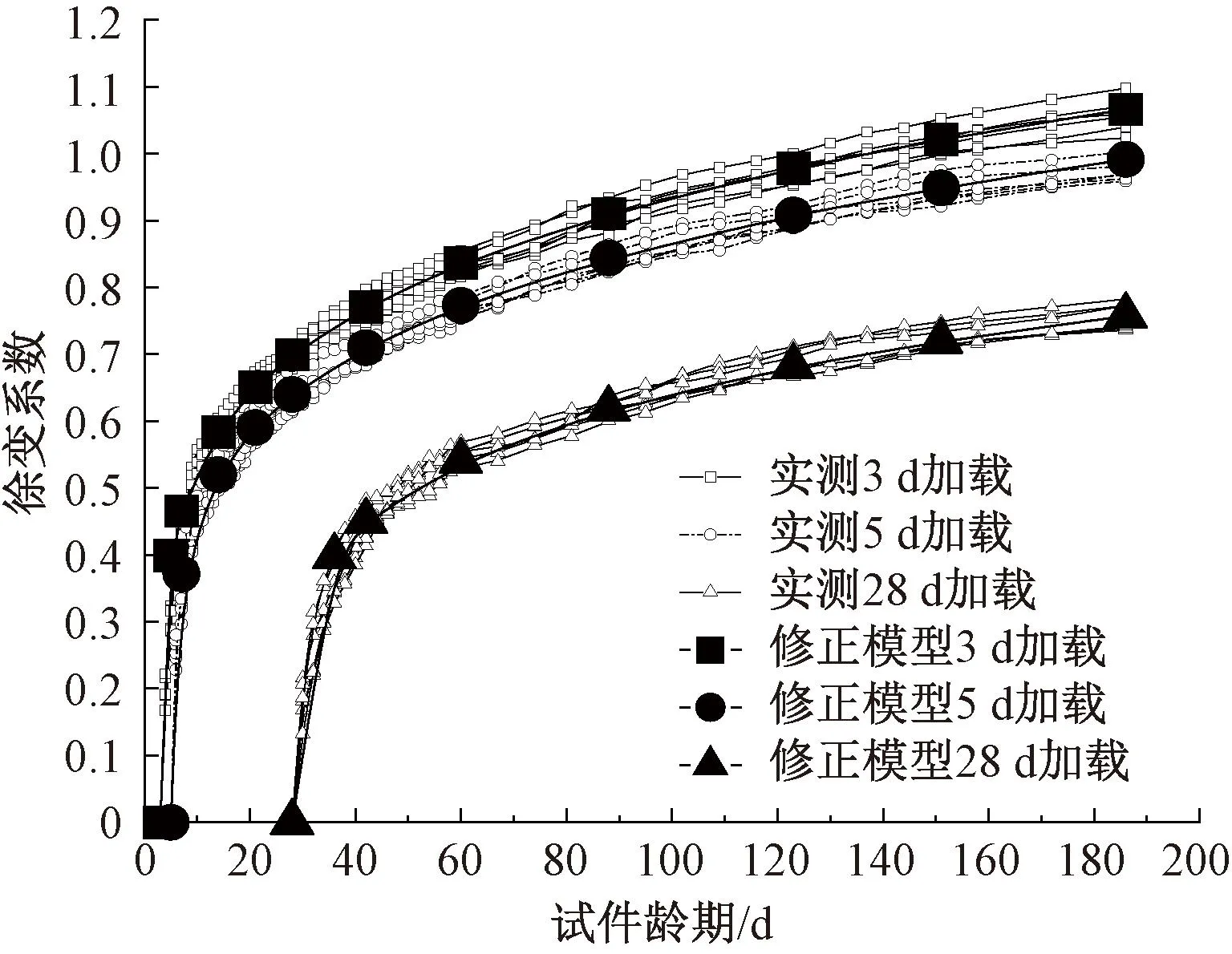
图14 修正预测模型与实测徐变系数对比

徐变的本质是混凝土硬结以后,骨料之间的水泥浆,部分变为结晶体,部分成为晶体间的凝胶体,具有黏性流动的性质。初始对混凝土施加外荷载时,在加荷的瞬时,结晶体与凝胶体共同承受外荷载;其后,随着时间的推移,凝胶体由于其黏性流动而逐渐卸荷,此时晶体承受了更多的外力,并产生弹性变形,从而使混凝土徐变增加,即这是由水泥凝胶体与水泥结晶体间应力重新分布所产生的结果。

从图14可以得出:校正后预测曲线的总体趋势与实测值吻合较好,可以用来预测本研究所用的HPC徐变发展规律。不足之处在于,载荷初期徐变进展有着些许的差异,不过在实际施工中该误差在允许范围之内。

4 结论

高性能混凝土受混凝土骨料、添加剂等材料因素影响,其主要特性时变规律与普通混凝土有较大的区别,因而现有规范中针对普通混凝土时变特性的预测理论及方法对高性能混凝土时变特性的适配性不足。鉴于此,本文采取桥梁施工同步进行的同位同条件试验,研究了寒冷地区海洋环境下高性能混凝土的时变特性,提出适用于高性能混凝土时变特性预测模型的简便修正公式。主要结论如下:

1)高性能混凝土抗压强度在初期(7 d内)发展迅速,之后随着时间的推进其抗压强度进展缓慢,最后趋于平稳;高性能混凝土早期抗压强度发展明显高于规范预测值,表明采取现有规范预测高性能混凝土抗压强度发展走向时,会低估其初期的抗压强度值。究其原因,高性能混凝土受自身材料、添加剂等因素影响,早期凝结及其强度发展迅速。

2)采用我国桥规JTG 3362—2018、CEB-FIP—2010以及EN 1992-2—2005规范推算得到的28 d龄期高性能混凝土弹性模量虽远大于规范标准值,但仍小于混凝土试块弹性模量实测值,这表明采用既有的规范强度预测方法来推算高性能混凝土的弹性模量参数不尽合理,仍然会低估其弹性模量参数,需要就高性能混凝土针对该参数进行专门研究。

3)高性能混凝土早期收缩发展迅速,在短时间内收缩应变急剧增大;此外混凝土构件尺寸不仅影响收缩应变的终值,而且影响收缩应变随时间的发展进程。同时直接套用现有规范公式预测方法会低估高性能混凝土收缩应变,最后针对高性能混凝土的收缩发展特性,发展了基于CEB-FIP—2010模型的参数修正预测模型。

4)高性能混凝土徐变发展特性加载后短时期内急剧增大,之后增长趋势随龄期增加逐渐减缓;而且加载应力越大,加载龄期越早,则徐变系数越大;高性能混凝土实测徐变发展规律与已有规范模型的预测规律存在一定的差别,具体来看,GL 2000模型预测结果偏大,AASHTO模型预测结果偏小。为了便于实际应用,本文针对相关研究参数,提出了基于欧洲规范EN 1992-2—2005修正的高性能混凝土徐变预测修正公式。

高性能混凝土时变性能演化机理与精确预测由于受多种不确定复杂因素影响,一直是研究的热难点。本研究主要从试验角度出发研究其性能时变发展规律,并基于现有规范提出了相应的修正预测公式,但对于该部分内容演化机理理论层面的推导还不够系统和深入,有待再后续工作中持续开展。